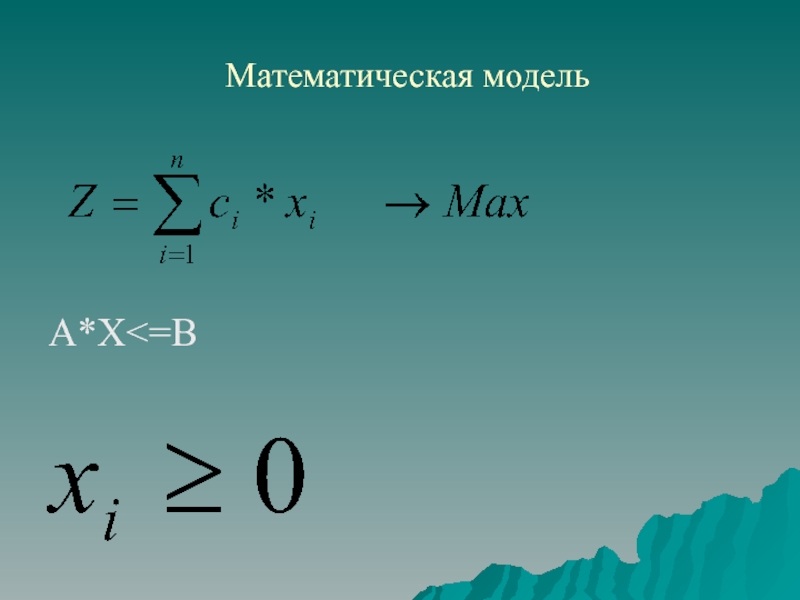Слайд 1Экономико – математическое моделирование
Слайд 2Список литературы
1 Р. М. Эйдинов. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ И ФИНАНСОВЫХ
СИТУАЦИЙ. Учебное пособие для студентов экономических и финансовых специальностей Екатеринбург,
2007
2. Р. М. Эйдинов. Курс лекций по дисциплине ЭММ для специальности МЭО, УрГЭУ,2008,(электронный варириант).
3. Р.М. Эйдинов. Финансово-экономическое моделирование. Екатеринбург, УрГЭУ, 1998. 4. А.А.Горчаков, И.В.Орлова. Компьютерные экономико-математические
модели. М., Компьютер, издательское объединение ""ЮНИТИ"",1995
Слайд 3Дополнительная литература
О.О. Замков, А.В. Толстопятенко и др. Мматематические методы в
экономике.
Е.В. Бережная, В.И. Бережной Математические методы моделирования экономических систем.
Е.М.
Кочкина, Е.В. Радковская Методы исследования и моделирования национальной экономики.
С. Ю. Юдин Моделирование систем и оптимизация их параметров. Электронный вариант (http://ser.t-k.ru)
Слайд 4Лекция 1
Экономическое развитие не может быть обоснованным и действенным без
опоры на новый научный фундамент. В рамках проведения количественного анализа
большую роль играет использование математического аппарата. Решение любой экономической задачи выполняется по определенной логической схеме, при этом должны быть выявлены основные экономические закономерности, присущие данному экономическому процессу или объекту.
Важнейшей процедурой во многом определяющим успех решения экономической задачи – процедура создания эмм.
Матем. модель – абстрактное отображение исследуемого объекта или процесса, в котором основные соотношения между экономическими показателями, характеризующими процесс или объект с помощью математических зависимостей.
Слайд 5Классификация ЭММ.
Основные классы
Макроэкономические модели – рассматривают экономику как единое целое,
связывают между собой укрупненные материальные и финансовые показатели: ВНП, инвестиции,
занятость.
Микроэкономические модели – для описания основных элементов экономической системы и различных форм взаимодействия элементов при заданных условиях (% ставки, инфляции, уровня безработицы)
Равновесные модели описывают такое состояние экономики, когда результирующая всех сил, стремящихся вывести ее из равновесия =0
Дескриптивные детерминированные модели описывают объекты с известными экономическими закономерностями. Которые нужно формализовать.
Слайд 6Оптимизационные модели характеризуются наличием критерия оптимальности и системой ограничений.
Детерминированные модели,
т.е. жесткие функциональные связи между параметрами модели.
Эконометрические модели.
Стохастические модели –
возможность случайных воздействий на исследуемые показатели.
Динамические модели – связь переменных во времени. Пример - модели экономической динамики, которая объясняет развитие национального хозяйства, относится и теория экономических циклов. Теория циклов призвана объяснить причины колебаний экономической активности общества во времени.
Слайд 7Оптимизационные модели
Можно выделить 3 этапа экономико-математического моделирования. На первом этапе
ставятся цели и задачи исследования, проводится качественное описание объекта.
На
втором этапе формируется математическая модель изучаемого объекта, производится выбор методов исследования, подбор программного обеспечения для ЭВМ, подготавливается исходная информация.
На третьем, основном, этапе выполняется анализ математической модели, обработка и анализ полученных результатов
Слайд 8В математическом моделировании выделяют задачи анализа и синтеза. В задачах
анализа в математической форме выявляются зависимости между различными экономическими показателями,
характеризующими изучаемый процесс или объект (экономические механизмы). Целью решения задач синтеза является разработка наиболее рациональных решений. Задачи синтеза в математическом отношении, как правило, сложнее задач анализа, и чаще всего решению задач синтеза предшествует решение нескольких задач анализа.
Слайд 9Система принятия решений должна охватывать полный цикл хозяйственных проблем. Такие
экономические проблемы, как закономерности ценообразования, изучение полных затрат труда и
материалов на единицу продукции, исследование межотраслевых связей, определение рентабельности капиталовложений, определение эффективного размещения производительных сил, оптимальное планирование производственного процесса, эффективное использование ограниченных ресурсов, календарное производственное планирование и многие другие, не менее важные, могут успешно решаться при широком привлечении математических методов исследования. Среди математических моделей экономических процессов особое место занимают так называемые оптимизационные модели, с помощью которых среди множества вариантов поведения выбирается наилучший (оптимальный) в том или ином смысле.
Слайд 10В качестве инструмента оптимизации наиболее часто используется математическое программирование (линейное,
нелинейное, динамическое и т.п.), которое входит в арсенал методов исследования
операций. Наиболее обобщенной моделью поиска оптимальных решений является общая задача математического программирования, формулируемая следующим образом
max (min) Z = f(x1,x2,...,xn) ,
Fi(x1,x2,...,xn) = Bi , i=1,2,...,m ,
xj 0 , j=1,2,...,n ,
Слайд 11где Z – оптимизируемая цель экономической системы, соответственно f(x1,x2,...,xn) –
целевая функция; x1,x2,...,xn – показатели степени использования средств достижения цели
(могут характеризовать выпуск продукции разных видов, загрузку оборудования, использование ресурсов и т.п.); Fi(x1,x2,...,xn) – функция совокупных затрат средств i-й группы, используемых для достижения цели; Вi – лимиты, предельные границы совокупных затрат средств i-й группы.
Переменные x1,x2,...,xn, которые удовлетворяют всем ограничениям задачи, называются допустимым решением или планом . Обозначим вектор переменных как
Слайд 12
Все допустимые решения образуют область определения задачи, или область допустимых
решений. Допустимое решение, максимизирующее (минимизирующее) целевую функцию, называется оптимальным решением
или оптимальным планом.
При решении задачи оптимального планирования в качестве целевой функции будем использовать линейную функцию, метод решения – симплекс метод линейного программирования.
Слайд 13Задача прямая и двойственная.
Прямая
Предприятие выпускает n изделий и использует
m ресурсов.
Найти оптимальный план выпуска.
Обозначим план выпуска
-ограничения
на используемые ресурсы.
Матрица А- нормы затрат ресурсов. норма затрат i ресурса на j изделие - прибыль от производства изделий
Слайд 14прибыль от производства изделий-
Целевая функция f(x1,x2,...,xn) имеет вид
Слайд 16Двойственная задача
Двойственная должна быть на мин. Новые переменные Y- используемые
ресурсы, решение двойственной задачи
ограничения двойственной задачи.
Ат –транспонированная матрица А
Слайд 18Сопоставляя формы записи прямой и двойственной задач, можно установить между
ними следующие взаимосвязи.
1. Если прямая задача является задачей максимизации, то
двойственная будет задачей минимизаци, и наоборот.
2. Коэффициенты целевой функции прямой задачи c1, .,cn становятся свободными членами ограничений двойственной задачи.
3. Свободные члены ограничений прямой задачи b1, .,bm становятся коэффициентами целевой функции двойственной задачи.
4. Матрица ограничений двойственной задачи получается путем транспортирования матрицы ограничений прямой задачи.
5. Знаки неравенств в ограничениях изменяются на противоположные.
6. Число ограничений прямой задачи равно числу переменных двойственной задачи, и наоборот.
Переменные y1,.,ym двойственной задачи иногда называют теневыми ценами.
Двойственную задачу выгоднее решать, чем прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений (m > n).
Связь между оптимальными решениями прямой и двойственной задач устанавливают, анализируя следующие теоремы теории двойственности
Слайд 19Основная теорема
Если одна из взаимодействующих задач имеет оптимальное решение, то
и вторая задача имеет оптимальное решение
Z(X*)=Z*(Y*)
Если X0 и
Y0 допустимые решения прямой и двойственной задач, то есть AX<=b и
A>=C , то
то есть значения целевой функции прямой задачи никогда не превышают значения целевой функции двойственной задачи.
.
Слайд 20Формирования оптимальной производственной программы
Предприятие характеризуется следующими параметрами:
- выпускается
N видов продукции;
- используется M видов ресурсов.
Известны:
- цена каждого вида
продукции;
- норма затрат каждого вида ресурсов для выпуска единицы каждого вида продукции;
- запас каждого вида ресурсов на текущий период.
Задача: Найти такой план выпуска продукции, для которого суммарная выручка от реализации всех видов продукции будет максимальной.
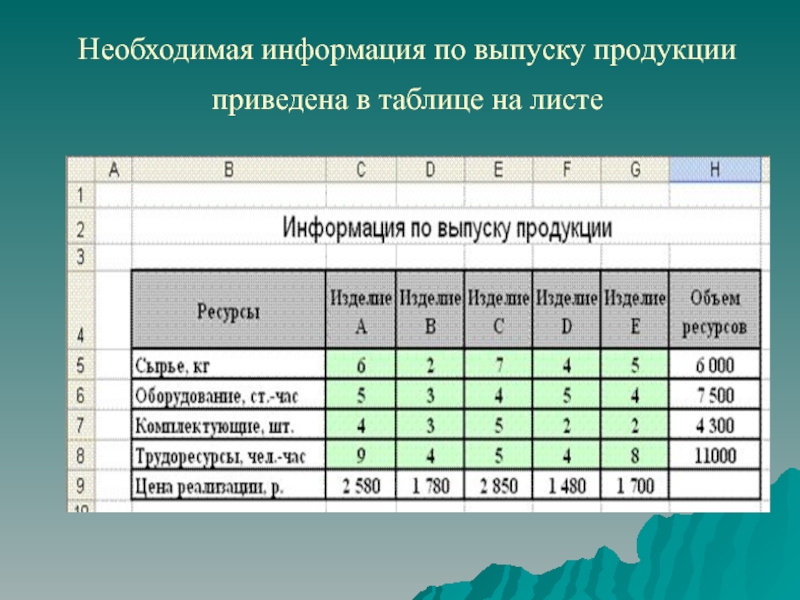
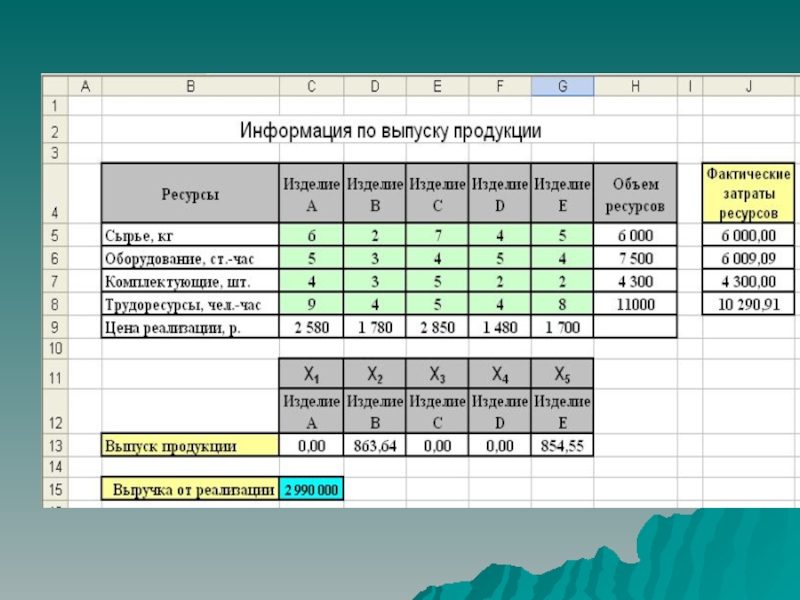
Слайд 21Необходимая информация по выпуску продукции приведена в таблице на листе
Слайд 22Здесь N=5 (пять видов изделий), а M=4 (четыре типа ресурсов).
Цены реализации каждого вида продукции находятся в ячейках C9:G9, нормы
затрат каждого вида ресурсов – в блоке ячеек C5:G8, а запасы ресурсов – в ячейках H5:H8.
Процедура решения задачи предполагает выполнение следующих этапов.
I этап. Выбор управляемых переменных
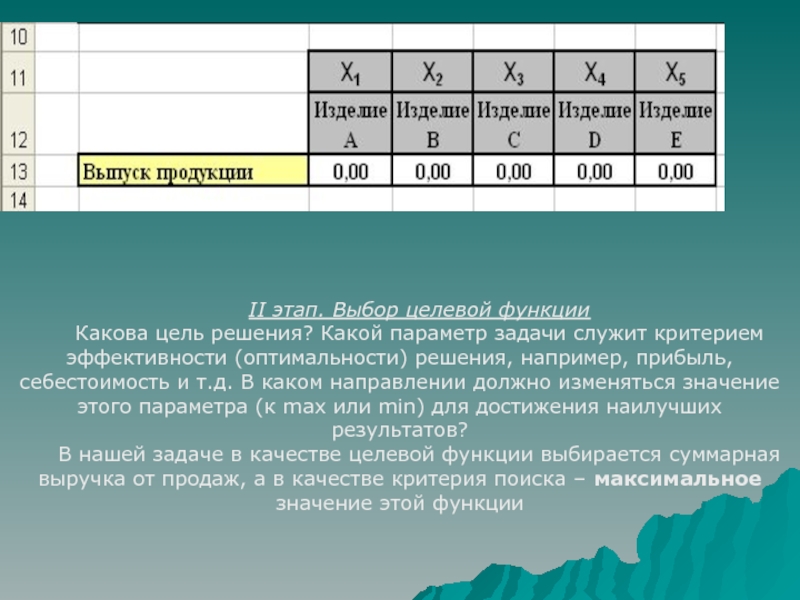
В качестве управляемых переменных выбираются те экономические показатели, которые позволяют записать все ограничения, а их численные значения дают ответ на вопрос, поставленный в задаче. Для нашего примера – это объемы выпускаемой продукции:
Xi – объем выпуска i-го вида продукции, i = 1, 2, 3, 4, 5.
Слайд 23II этап. Выбор целевой функции
Какова цель решения? Какой параметр задачи
служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость и т.д.
В каком направлении должно изменяться значение этого параметра (к max или min) для достижения наилучших результатов?
В нашей задаче в качестве целевой функции выбирается суммарная выручка от продаж, а в качестве критерия поиска – максимальное значение этой функции
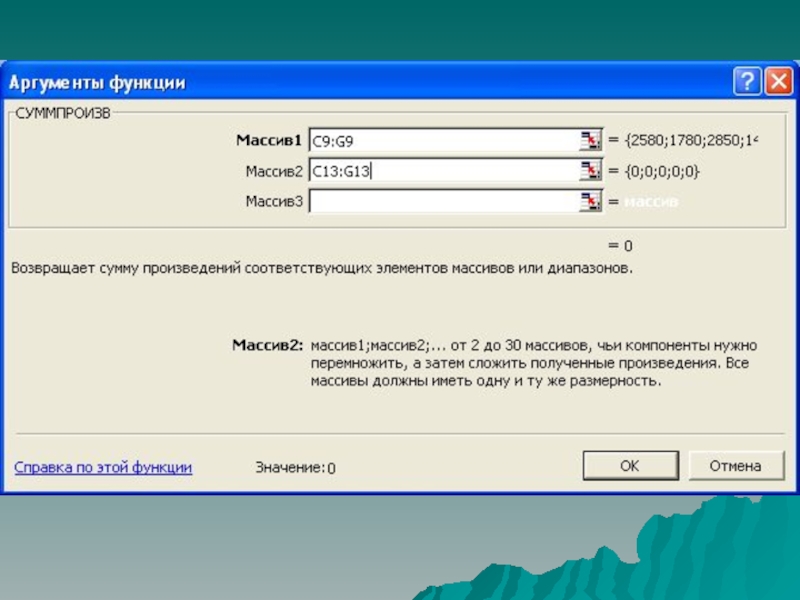
Слайд 24Можно записать математическое выражение для расчета суммарной выручки от продаж:
Z
= 2 580 ∙ Х1 + 1 780 ∙ Х2 +
2 850 ∙ Х3 + 1 480 ∙ Х4 + 1 700 ∙ Х5 .
В качестве коэффициентов целевой функции в данной задаче служат значения цен реализации каждого вида изделий. Для построения этой формулы в рамках Excel используется функция СУММПРОИЗВ(). Эта функция возвращает сумму произведений соответствующих элементов диапазонов. В нашем примере – это диапазоны C9:G9 (данные по цене реализации) и C13:G13 (управляемые переменные).
Слайд 26I I I этап. Анализ существенных ограничений
Какие условия в отношении
искомых величин и ресурсов задачи должны быть выполнены? Например, количество
ресурса, затраченного при производстве и его запас на складе; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.
Учесть в математической модели все факторы, оказывающие влияние на выпуск продукции, невозможно, более того, в этом нет необходимости. Следует учесть только те факторы, которые оказывают существенное влияние на принимаемые решения.
Важно:
В оптимизационных моделях различают три типа ограничений:
1) ограниченность имеющихся ресурсов;
2) необходимость достижения экономическими показателями заранее заданных значений (плановые ограничения);
3) технологические соотношения между группами управляемых переменных.
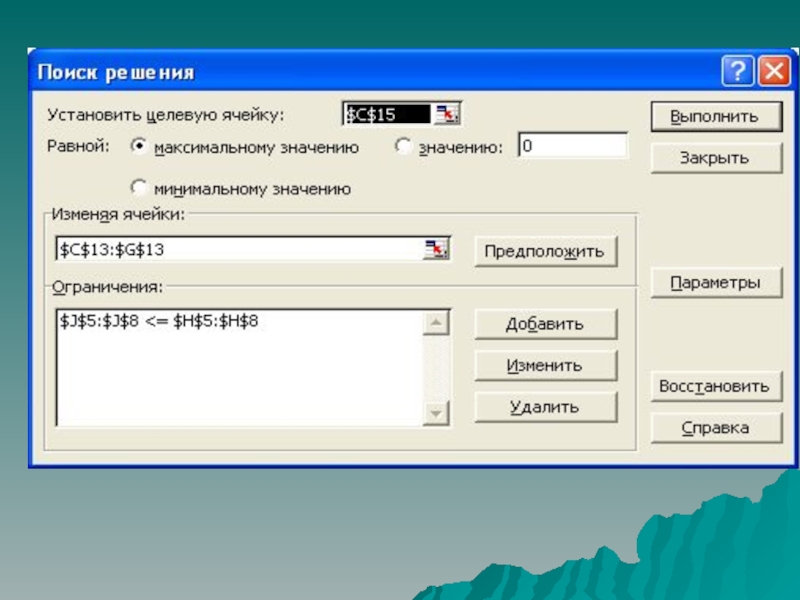
Слайд 27Процедура решения задачи в среде Excel
Выполнить: пункт меню Сервис –
Поиск решения. Или
Пункт меню «Данные»- Поиск решения.
Заполнить диалоговое окно
по образу
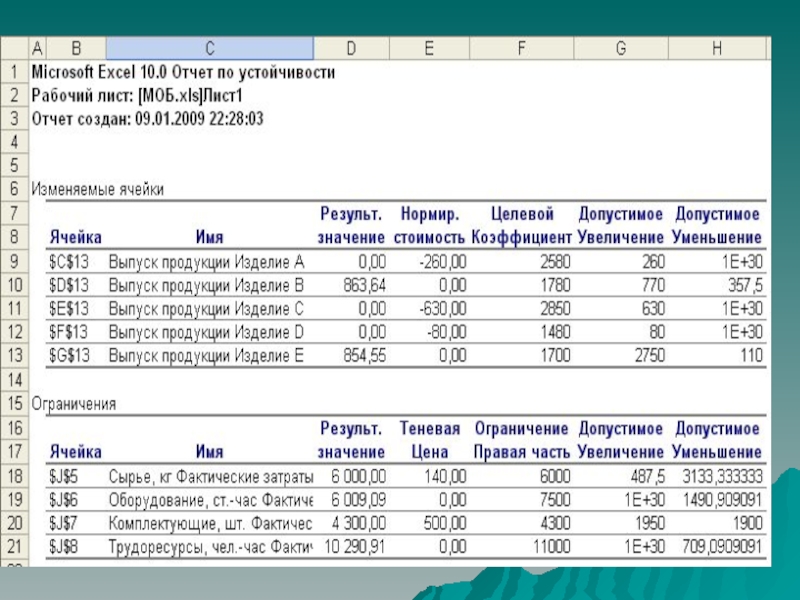
Слайд 34Нормированная стоимость.
Нормированная стоимость показывает величину изменения целевой функции при
увеличении соответствующей управляемой переменной на одну единицу.
В нашем случае
Х1 = 0, Х3 = 0 и Х4 = 0. Если бы в математическую модель было добавлено ограничение Х1 = 1, то величина целевой функции снизилась бы на 260, так как нормированная стоимость для переменной Х1 равна –260. Соответственно, принудительное включение в выпуск одной единицы изделия С приведет к сокращению величины денежной суммы на 630 р., а изделия D – на 80 р.
Согласно теории двойственности нормированная стоимость для изделий, вошедших в выпуск, всегда равна нулю (в нашем случае изделия В и Е).
Иногда возникает ситуация, когда управляемая переменная равна нулю и имеет нулевую нормированную стоимость. Такая ситуация носит название альтернативного оптимума. В этом случае можно получить множество оптимальных вариантов выпуска продукции с сохранением оптимальной величины целевой функции.
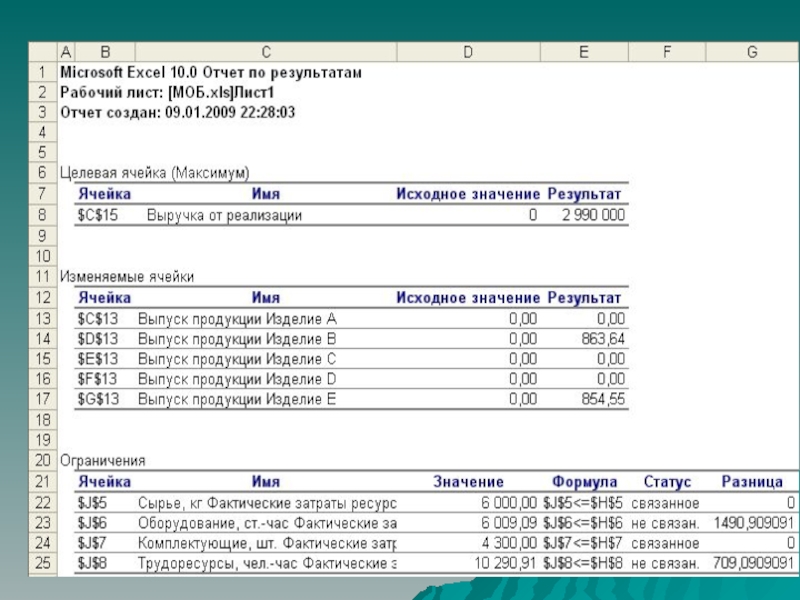
Слайд 35Оптимальное решение характеризуется тремя основными показателями: структурой выпуска, объемами выпуска
и величиной целевой функции.
Структура выпуска – это перечень изделий, вошедших
в выпуск.
В нашем случае структуру выпуска определяют изделия В и Е.
Объемы выпуска – это то количество каждого вида изделий, которое выпускает предприятие. У нас изделия А, С и D не выпускаются, т.е. их объемы равны нулю, изделие В выпускается в объеме 863,64 ед., а изделие Е – в объеме 854,55 ед.
Слайд 36ВЫВОДЫ:
1. Если изделие вошло в программу выпуска:
- изменение целевого коэффициента
внутри интервала устойчивости не меняет структуру и объем выпуска, но
меняет величину целевой функции.
- при выходе целевого коэффициента за нижнюю границу интервала устойчивости изделие становится менее рентабельным или нерентабельным и, либо снимается с выпуска, либо сокращается объем его производства. Освободившиеся ресурсы направляются на выпуск другой, более рентабельной, продукции. Меняются структура и объемы выпуска, ухудшается величина целевой функции;
- при выходе целевого коэффициента за верхнюю границу интервала устойчивости рентабельность изделия возрастает настолько, что следует наращивать его выпуск за счет другой, менее рентабельной, продукции. Меняются структура и объемы выпуска, улучшается величина целевой функции.
2. Если изделие не вошло в программу выпуска:
- изменение целевого коэффициента внутри интервала устойчивости не меняет величину целевой функции, структуру и объемы выпуска.
- при выходе целевого коэффициента за верхнюю границу интервала устойчивости изделие становится рентабельным и включается в выпуск за счет другой, менее рентабельной, продукции. Меняются структура и объемы выпуска, улучшается величина целевой функции.

Слайд 37I I. Теперь проведем исследование, как изменение запасов ресурсов влияет
на изменение оптимального решения, т.е. на результаты выпуска.
В таблице Ограничения
Отчета по устойчивости содержится информация об исходных значениях правых частей ограничений (столбец Ограничение, правая часть) и о значениях левых частей ограничений, получаемых в результате решения задачи (столбец Результирующее значение).
В нашем случае столбец Ограничение, правая часть содержит информацию о исходных запасах используемых в производстве ресурсов.
В столбце Результирующее значение выведена информация о реальных затратах каждого ресурса.
Особый интерес представляют значения столбца Теневая цена. Теневая цена показывает величину изменения целевой функции при увеличении правой части соответствующего ограничения на одну единицу.
Например, увеличение запаса сырья на 1 кг приведет к росту целевой функции на 140 руб. Увеличение фонда времени оборудования в выпуске продукции ничего не изменит. Увеличение количества комплектующих на 1 шт. приведет к росту целевой функции на 500 руб. Увеличение трудовых ресурсов, как и фонда времени оборудования, в выпуске продукции ничего не изменит.

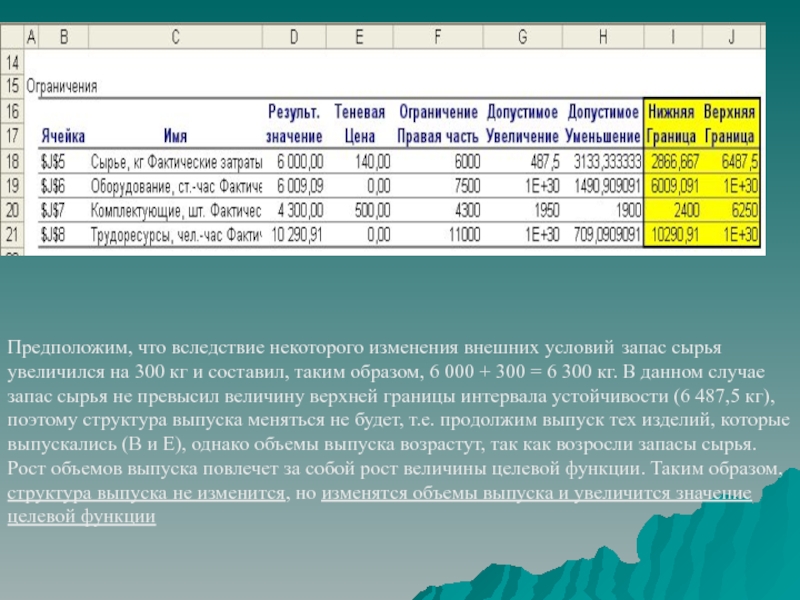
Слайд 38Предположим, что вследствие некоторого изменения внешних условий запас сырья увеличился
на 300 кг и составил, таким образом, 6 000 +
300 = 6 300 кг. В данном случае запас сырья не превысил величину верхней границы интервала устойчивости (6 487,5 кг), поэтому структура выпуска меняться не будет, т.е. продолжим выпуск тех изделий, которые выпускались (В и E), однако объемы выпуска возрастут, так как возросли запасы сырья. Рост объемов выпуска повлечет за собой рост величины целевой функции. Таким образом, структура выпуска не изменится, но изменятся объемы выпуска и увеличится значение целевой функции
Слайд 39ВЫВОДЫ:
1. Если ресурс израсходован полностью (является дефицитным)
- Изменение запаса
ресурса внутри интервала устойчивости не меняет структуру, но меняет объемы
выпуска и, соответственно, величину целевой функции.
- Выход величины запаса ресурса за границу интервала устойчивости приводит к изменению структуры выпуска, объемов выпуска и величины целевой функции.
2. Если ресурс имеется в избытке (не является дефицитным)
- Изменение запаса ресурса внутри интервала устойчивости в выпуске продукции ничего не меняет: сохраняются структура выпуска, объемы выпуска и величина целевой функции.
- Выход величины запаса ресурса за нижнюю границу интервала устойчивости (верхняя граница для избыточного ресурса всегда равна бесконечности) приводит к изменению структуры выпуска, объемов выпуска и снижению величины целевой функции.