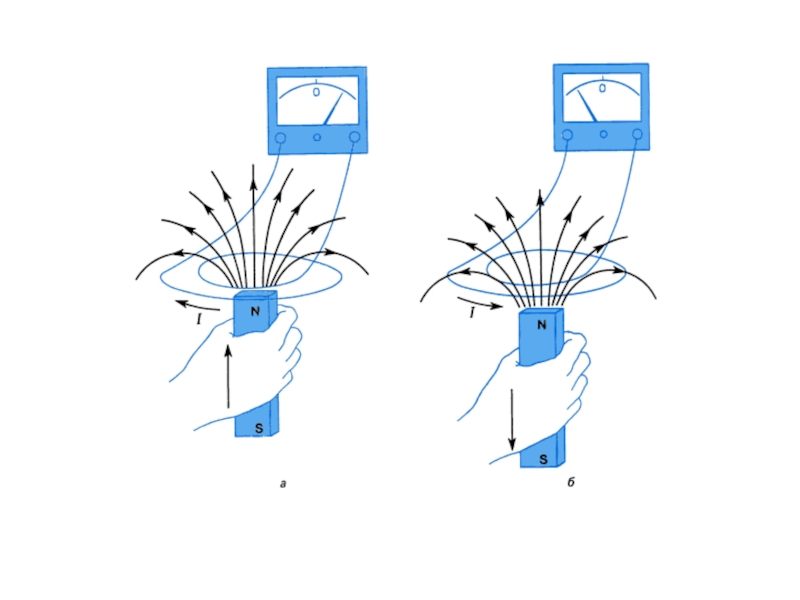
Электромагнитная индукция В 1831 г. английский физик М. Фарадей, открыл явление

электромагнитной индукции, которое заключается в том, что в замкнутом проводящем

Направление индукционного тока определяется правилом Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей

изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре

Знак минус отражает правило Ленца

движения контура в постоянном магнитном поле объясняется действием силы Лоренца,

Максвелл предположил, что всякое переменное магнитное поле возбуждает в окружающем

Циркуляция вектора E этого поля по любому неподвижному контуру L проводника представляет собой э. д. с. электромагнитной индукции:

C другой стороны по закону Фарадея:

Приравняв эти выражения получим:

Циркуляция электрического поля, создаваемого изменяющимся магнитным полем отлична от нуля, значит, это поле не является потенциальным, а является как и магнитное поле вихревым.

себя магнитное поле, индукция которого, пропорциональна току:
Магнитный поток
Следовательно
Запишем в

Коэффициент пропорциональности L называется индуктивностью контура. Индуктивность зависит от геометрических размеров и формы контура, а также от магнитных свойств окружающей среды.

Единицей индуктивности является генри (Гн). Индуктивностью 1Гн обладает контур, магнитный поток сквозь который при силе тока 1А равен 1Вб

B=B(I).
2). Вычислить полный магнитный поток:
3). Определить индуктивность, воспользовавшись

N витков, по которому течет ток I . Длину соленоида

Индукцию магнитного поля внутри соленоида рассчитаем, применяя теорему о циркуляции.

Выберем замкнутый прямоугольный контур ABCDA, как показано на рис.

Циркуляция вектора B по замкнутому контуру ABCDA, охватывающему все N витков, равна

На участках ВС и DA контур перпендикулярен линиям магнитной

Остается только один интеграл:

Выражение для магнитной индукции поля внутри соленоида примет вид:

n=N/l - число витков на единицу длины

Магнитное поле внутри соленоида однородно.

магнитный поток, пронизывающий N витков, равен
3). Вычислим индуктивность соленоида
V=Sl

Для соленоида с сердечником:

 - магнитная проницаемость среды

в нем силы тока называется самоиндукцией.
Для получения выражения для э.д.с.

Если при изменении тока индуктивность L остается постоянной, то

Знак минус показывает, что s всегда направлена так, чтобы препятствовать изменению силы тока

близко друг от друга.
Если в контуре 1 течет ток,

Часть магнитного потока, которая пронизывает контур 2

где L21 — коэффициент пропорциональности.

Если ток I1 изменяется, то в контуре 2 индуцируется э.д.с. i2, которая по закону Фарадея равна

поле изображено штриховыми линиями) пронизывает первый контур.
Часть магнитного потока,

Если ток I2 изменяется, то в контуре 1 индуцируется э.д.с. i1, которая по закону Фарадея равна

Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией.

L12 и L21 зависят от геометрической формы, размеров, взаимного расположения

При отсутствии ферромагнетиков

(Теорема взаимности).

Единица взаимной индуктивности — генри (Гн)

ток I.
Магнитный поток, создаваемый полем этого тока
При изменении

Для изменения магнитного потока необходимо совершить работу

Тогда работа по созданию магнитного потока Ф будет равна

поля непосредственно через индукцию магнитного поля B на примере соленоида.
Так

Индукция магнитного поля соленоида равна

Выразим

Подставим в выражение для энергии магнитного поля

магнитного поля получено для однородного поля, но оно справедливо и

- диэлектрическая проницаемость среды
- электрическая постоянная
Для сравнения:

внести вещество, то поле изменяется, так как всякое вещество способно

Это можно объяснить тем, что каждый движущийся вокруг ядра атома электрон представляет собой элементарный круговой ток.

В отсутствие внешнего поля орбиты молекулярных токов, а, следовательно, и их магнитные моменты

ориентированы хаотически в пространстве так, что вещество не проявляет никаких магнитных свойств.

При наложении внешнего магнитного поля моменты ориентируются вдоль силовых линий этого поля - вещество намагничивается.

Для вычисления индукции макроскопического поля, молекулярные токи можно заменить

Рассмотрим намагниченный цилиндр из однородного материала.

Некомпенсированными остаются только те молекулярные токи, которые выходят на боковую поверхность цилиндра.

Эти токи образуют макроскопический поверхностный ток I’, циркулирующий по боковой поверхности цилиндра, который создает такое же макроскопическое поле, что и все молекулярные токи вместе взятые.

равна алгебраической сумме токов намагничивания, охватываемых этим контуром:
Напряженность магнитного поля

Циркуляция вектора B, определяется не только токами проводимости, но и токами намагничивания

Выражая ток намагничивания через циркуляцию вектора намагниченности, получим

Величину, стоящую в скобках, называют напряженностью магнитного поля:

равна алгебраической сумме токов проводимости, охватываемых этим контуром.
Размерность напряженности магнитного

Вектор намагниченности и напряженность магнитного поля связаны следующим соотношением:

где  - магнитная восприимчивость, зависящая от свойств магнетика.

<0 для диамагнетиков

>0 для парамагнетиков

Для диамагнетиков
Для парамагнетиков