Слайд 2Спектр - в физике — распределение значений физической величины.
Обычно под спектром подразумевается электромагнитный спектр —
распределение энергии электромагнитного излучения по частотам или по длинам волн.
В научный обиход
термин «спектр» ввёл Ньютон в 1671—1672 годах для обозначения многоцветной полосы, похожей на радугу, которая получается при прохождении солнечного луча через треугольную стеклянную призму.
Исаак Ньютон
Слайд 4
При исследовании строения химических соединений, наибольшую информацию можно получить
при изучении взаимодействия вещества с электромагнитным излучением.
Электромагнитное излучение -
простая гармоническая волна, распространяющаяся от источника в отсутствии отражения или преломления по прямым линиям.
Излучение состоит из энергетических пакетов (квантов), называемых фотонами, которые движутся со скоростью света.
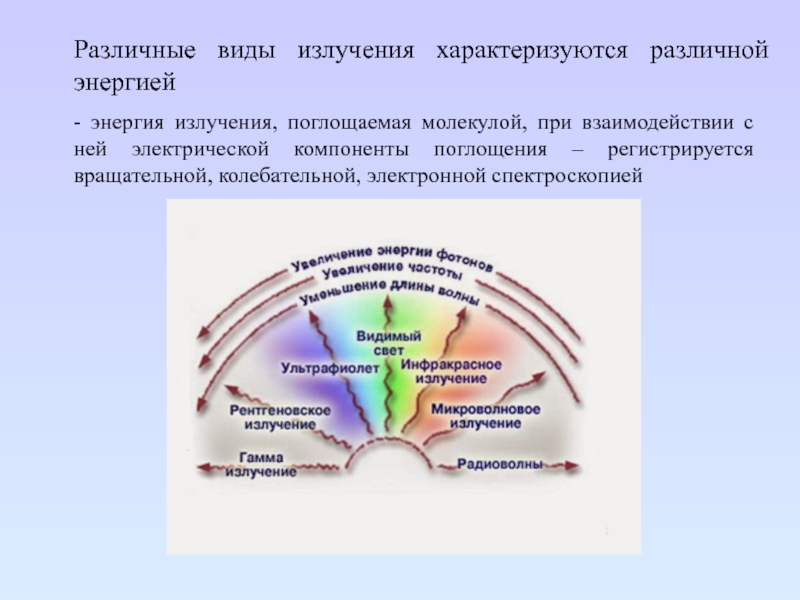
Слайд 5Различные виды излучения характеризуются различной энергией
- энергия излучения, поглощаемая
молекулой, при взаимодействии с ней электрической компоненты поглощения – регистрируется
вращательной, колебательной, электронной спектроскопией
Слайд 6 Условия поглощения излучения:
энергия излучения должна совпадать с
разностью энергий квантованных уровней ∆Е, соответствующих различным состояниям молекулы
Длину
волны λ такого излучения можно определить из
уравнения Бора:
∆Е = Е* - Е0 = hΰ
Е0 – энергия основного состояния;
Е* – энергия возбужденного состояния;
h – постоянная Планка
ΰ – частота излучения, ΰ = с/ λ
Слайд 7Е*>Е0 происходит поглощение света – спектры поглощения
Е0 > Е*
происходит излучение энергии - эмиссионные спектры
- при поглощении одного
кванта энергии молекула переходит в состояние с более высокой энергией.
Данное уравнение объединяет волновую и корпускулярную теории света.
Слайд 9Излучение можно охарактеризовать:
длиной волны λ
волновым числом υ
частотой
ΰ
Эти параметры связаны между собой уравнениями:
ΰ (с-1) =
∆Е = hcυ
При описании полос поглощения прибегают к разным единицам измерения:
υ : см-1
λ: 1см = 108А0 = 107нм = 104мкм
ΰ: 1с-1 = Гц
Е: 1 см-1 = 2,858 ккал/моль = 1,986 эрг/молекула = 1,24.10-4 эВ/моль.
∆Е (ккал/моль) ∙ λ (А0) = 2,858 ∙105
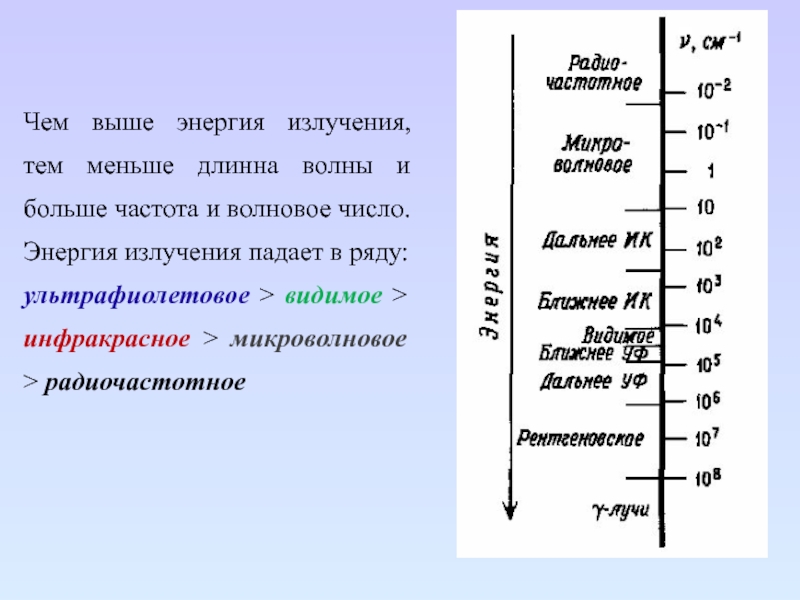
Слайд 12Чем выше энергия излучения, тем меньше длинна волны и больше
частота и волновое число.
Энергия излучения падает в ряду:
ультрафиолетовое >
видимое > инфракрасное > микроволновое > радиочастотное
Слайд 13 Электронные спектры поглощения возникают в результате переходов электронов из основного
в возбужденное состояние.
Для возбуждения электрона
от одного энергетического состояния до другого в большинстве случаев необходима энергия в интервале 60 – 150 ккал/моль.
Для такого возбуждения требуется видимый или УФ свет.
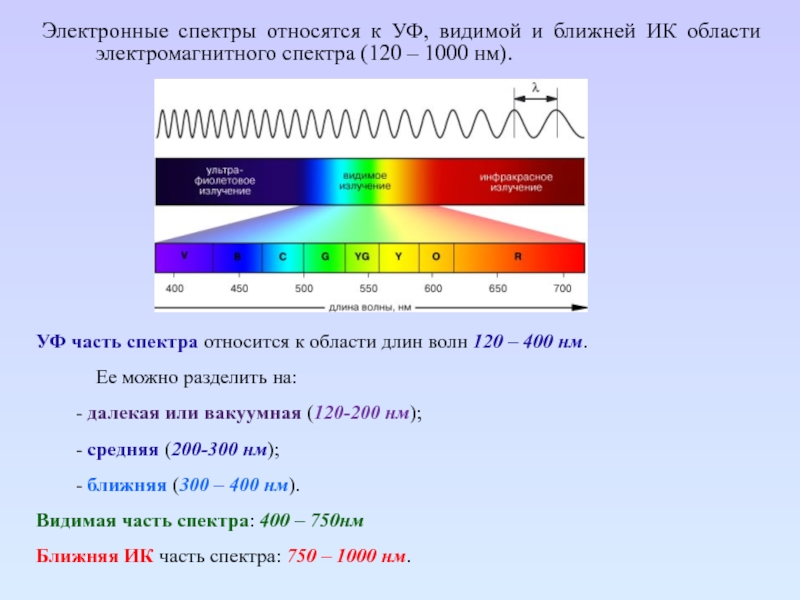
Слайд 14Электронные спектры относятся к УФ, видимой и ближней ИК области
электромагнитного спектра (120 – 1000 нм).
УФ часть спектра относится к
области длин волн 120 – 400 нм.
Ее можно разделить на:
- далекая или вакуумная (120-200 нм);
- средняя (200-300 нм);
- ближняя (300 – 400 нм).
Видимая часть спектра: 400 – 750нм
Ближняя ИК часть спектра: 750 – 1000 нм.
Слайд 16Законы поглощения света
Для оптических спектров имеются общие законы поглощения
излучения, дающие соотношение между величиной поглощения и количеством поглощающего вещества.
Все они справедливы для монохроматического излучения.
Пьер
Бугер
Иоганн Генрих Ламберт
Август
Бер
Слайд 17k = 0,434k/
- закон Бугера - Ламберта
Первый закон выражает
зависимость между интенсивностью прошедшего излучения и толщиной слоя поглощающего вещества.
Поток
параллельных лучей монохроматического света при прохождении через гомогенную поглощающую среду ослабляется по экспоненциальному закону
I0 – интенсивность падающего монохроматического излучения;
I – интенсивность прошедшего монохроматического излучения;
k/ – коэффициент поглощения, являющийся индивидуальной характеристикой вещества для каждой длины волны.
l - толщина поглощающего слоя
Слайд 18 Второй закон выражает связь между интенсивностью прошедшего излучения и концентрацией
поглощающего вещества в растворе: поток параллельных лучей монохроматического излучения при
прохождении через раствор поглощающего вещества концентрацией с ослабляется по закону:
Если концентрацию выражается в моль/л, l – см, то коэффициент поглощения называется молярным коэффициентом поглощения (молярной экстинкцией) и обозначается ε
ε – мера поглощающей способности вещества
Зависимость всегда является линейной при соблюдении условия монохроматического излучения и отсутствия превращений вещества в растворе (ассоциация или диссоциация).
- закон Бера
Слайд 20Способы изображения электронных спектров
Электронные спектры поглощения записываются в виде
зависимости двух переменных величин – фактора интенсивности (оптическая плотность, молярный
коэффициент экстинкции и т.д.) и фактора длины волны (длина волны, волновое число).
Электронный спектр фенантрена в различных координатах
Если необходимо охарактеризовать УФ - спектр не прибегая к его изображению, то принято перечислять координаты максимумов кривой поглощения, например:
λmaxметанол, нм (ε): 220 (13900), 272 (21600)
Слайд 21Природа электронных спектров
При обработке молекулярных спектров пользуются приближением Борна
– Оппенгеймера: полная энергия системы рассматривается как сумма трех независимых
энергий - электронной, колебательной, вращательной.
E = Eэл. + Ек.+ Евр.
Полная волновая функция молекулы является произведением функций электронного, колебательного и вращательного состояний.
Ψ = Ψэл. Ψк. Ψвр.
Изменения в электронном состоянии молекулы происходит при возбуждении связывающего или несвязывающего электрона от основного состояния до вакантной МО более высокой энергии.
Колебательные энергетические состояния характеризуются колебанием атомов в молекуле.
Вращательные состояния соответствуют квантовым молекулярным вращениям вокруг оси (вращение вокруг оси С2 в молекуле SO2) без заметного изменения длин связей или валентных углов.
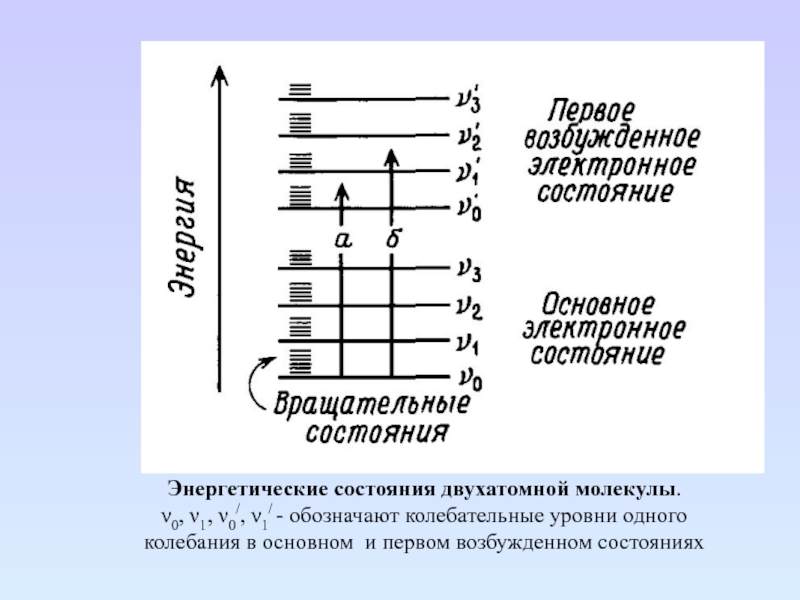
Слайд 22Энергетические состояния двухатомной молекулы.
ν0, ν1, ν0/, ν1/ - обозначают колебательные
уровни одного колебания в основном и первом возбужденном состояниях
Слайд 23Колебательные и электронные энергетические уровни двухатомной молекулы
Для каждого электронного
состояния характерна своя функция потенциальной энергии. У двухатомной молекулы она
может быть представлена функцией Морзе, т. е. имеется зависимость от расстояния между ядрами r. Каждая горизонтальная линия соответствует своему колебательному энергетическому состоянию. Основное состояние обозначается как ν0, а возбужденные – как ν1, ν2 и т.д.
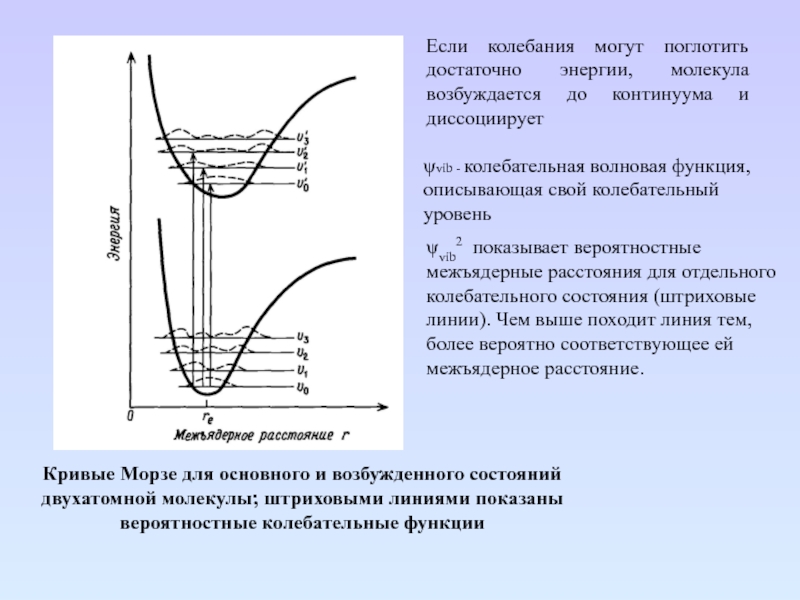
Слайд 24Кривые Морзе для основного и возбужденного состояний двухатомной молекулы; штриховыми
линиями показаны вероятностные колебательные функции
ψvib - колебательная волновая функция, описывающая
свой колебательный уровень
ψvib2 показывает вероятностные межъядерные расстояния для отдельного колебательного состояния (штриховые линии). Чем выше походит линия тем, более вероятно соответствующее ей межъядерное расстояние.
Если колебания могут поглотить достаточно энергии, молекула возбуждается до континуума и диссоциирует
Слайд 25Основные положения электронный спектроскопии
Принцип Франка – Кондона.
За то очень короткое время, которое необходимо для электронного перехода
(10-15с), атомы в молекуле не успевают заметно изменить свои положения. Поскольку электронный переход очень быстр, молекула в возбужденном состоянии будет иметь ту же самую молекулярную конфигурацию и колебательную кинетическую энергию, как и в момент поглощения фотона в основном состоянии. В результате все электронные переходы на кривой потенциальной энергии Морзе можно обозначить вертикальными линиями, связывающими основное и возбужденные состояния, т. е. во время перехода расстояния между ядрами не меняются.
Джеймс Франк
Эдвард Улер Кондон
Слайд 272. Правило отбора
Общего правила отбора, которое налагало бы ограничения
на изменения в колебательном состоянии, сопровождающие электронный переход не существует.
Часто электронные переходы происходят с основного колебательного уровня основного электронного состояния на многочисленные колебательные уровни данного возбужденного состояния. Такие переходы могут дать колебательную тонкую структуру основной полосы электронного перехода.
Три перехода могут привести к трем линиям. Переходы с основного уровня (ν0) на ν0/, ν1/, ν2/ обозначаются как переходы 0→0, 0→1, 0→2 соответственно.
Слайд 28Относительная интенсивность различных колебательных подполос зависит от колебательной волновой функции
для различных уровней. Переход выгоден, если вероятности нахождения молекулы и
в основном, и в возбужденном состояниях для одного и того же расстояния между ядрами велики.
Переход 0→0 является переходом низшей энергии с самой длинноволновой полосой. Разница в длинах волн, которые характеризуют эти полосы, представляет собой разность энергий колебательных уровней возбужденного состояния молекулы.
Слайд 293. Требование по симметрии
электронных переходов.
Приведенное выше обсуждение касалось
двухатомной молекулы, но основные его положения применимы и к многоатомным
молекулам. Часто функциональную группу многоатомной молекулы можно рассматривать как двухатомную (например, С=О в кетоне или альдегиде).
Истинные энергии результирующих молекулярных орбиталей функциональной группы будут подвержены влиянию электронных и стерических факторов, а также эффектов сопряжения, обусловленных другими атомами. В более сложных случаях, в которых переход затрагивает несколько атомов в молекуле (т.е. в случае делокализованной системы), для представления кривых потенциальной энергии необходима поверхность многих измерений.
Слайд 30 По аналогии с теорией молекулярных орбиталей:
переход молекулы из основного состояния в возбужденное соответствует переходу валентного
электрона с занятой связывающей МО на вакантную антисвязывающую.
Каждый электронный переход имеет свое обозначение
трем типам МО – σ, π, n – соответствует четыре типа электронных переходов:
Классификация электронных переходов
σ → σ*, π → π*, n → σ*, n → π*
Слайд 31Последовательность энергетических уровней электронов в молекуле органических соединений:
Слайд 32 σ → σ* - вакуумная УФ -
100 - 200 нм, (предельные углеводороды)
π →
π* – средняя, ближняя УФ - 200 - 400 нм, (непредельные углеводороды)
n → σ* - ближняя УФ - 300 – 400 нм,
(имеют место в случае насыщенных молекул, связанных одинарной связью с атомами, имеющими непоселенную электронную пару: С-OH, C-NH2, C-Hal)
n → π* - ближняя УФ, видимая область –
300 - 800нм,
(C=O, C=S, -N=N- и т. д.)
Слайд 33 Элементы симметрии – оси, плоскости, центры инверсии
Операцией симметрии молекулярной системы называют такое ее движение относительно соответствующего
элемента симметрии, которое переводит молекулярную систему в новое положение, физически тождественное первоначальному (поворот относительно оси, отражение в зеркальной плоскости и т.д.).
Более детальная классификация электронных переходов осуществляется с помощью анализа симметрии состояний
Для этого необходимо:
- знать симметрии волновых функций каждой орбитали → рассмотреть преобразование волновой функции орбитали по отношению к элементам симметрии молекулы → по теории групп установить к какому типу симметрии относится данная молекулярная орбиталь.
Слайд 34 Типы симметрии состояний молекулы:
А – симметрия относительно главной поворотной
оси
В – антисимметрия относительно главной поворотной оси
Нижние
индексы соответствуют симметрии (индекс 1) или антисимметрии (индекс 2) по отношению к плоскости, проходящей через главную ось. Полносимметричное представление всегда обозначается как А1
В точечных группах, включающих центр инверсии, добавляются индексы g (симметрия по отношению к центру инверсии) и u (антисимметрия по отношению к центру инверсии).
Если два или более состояний имеют одинаковую энергию, то они называются вырожденными и обозначаются:
Е – дважды вырожденное
Т – трижды вырожденное
Для орбиталей обычно применяют обозначения со строчными буквами: a, b, e, t.
Слайд 35 Электронные переходы в карбонильной группе формальдегида
Относительные энергии молекулярных орбиталей карбонильной
группы H2CO
Последовательность молекулярных орбиталей, на которых находятся валентные электроны молекулы,
имеет вид:
Молекулярными орбиталями карбонильной группы являются: σ, π, na, nb, π*, σ*
Слайд 36Формы молекулярных орбиталей формальдегида
Слайд 37 Для нахождения симметрии МО определяем полную симметрию молекулы, которая в
данном случае относится к С2v. Далее обращаемся к таблице характеров
группы С2v.
Операции симметрии E, C2, Gv(xz), Gv(yz) осуществленные над π – орбиталью приводят к характерам +1, -1, +1, -1. Этот ряд соответствует неприводимому представлению B1. В таком случае говорят, что орбиталь принадлежит к типу b1. Аналогично если подвергнуть упомянут выше операциям симметрии орбиталей na, nb, π*, σ* формальдегида, то получим, что эти орбитали принадлежат неприводимым представлениям a1, b2, b1, и a1 соответственно.
Слайд 38 В основном состоянии на каждой МО находится по два электрона
и оно всегда является полносимметричным А1. Электронное состояние будет характеризоваться
спином s = 0, т.е. будет синглетным. Мультиплетность выражается в виде удвоенной суммы спинов плюс 1: 2s+1.
синглетное триплетное
состояние состояние
Если при переходе электрона в возбужденное состояние спин электрона изменяется и возбужденное состояние содержит два неспаренных электрона с идентичным магнитным спиновым числом, то мультиплетность будет равна трем. Такой переход называется триплетным состоянием. Если электронный спин молекулы не меняется, то возбужденное состояние имеет мультиплетность равную единице – синглетное состояние.
Слайд 39 Зная симметрию орбиталей в основном состоянии можно определить симметрию возбужденного
состояния.
Тип симметрии состояния является произведением типов симметрии каждой орбитали, на
которой находится неспаренный электрон.
Ψе = Пφi(qi,Gi), qi – пространственные координаты, Gi – спиновые координаты.
Для этого образуют так называемое прямое произведение, т. е. перемножают характеры неприводимых представлений (каждой операции симметрии) соответствующих типов симметрии (строк) таблицы характеров. Рассматривая полученный ряд значений как строку характеров представлений данной точечной группы, однозначно определяют тип симметрии прямого произведения.
В случае формальдегида для волновой функции основного состояния можно записать прямое произведение:
Ψ0 = a12 · b12 · a12 · b22 = 1А1
Слайд 41
В состоянии, возникающем при переходе n→π*, по одному неспаренному электрону
находится на орбитали n симметрии b2 и на орбитали π*
симметрии b1. Прямое произведение имеет вид:
Результирующим неприводимым представлением является А2. Таким образом, возбужденное состояние, получающееся при этом переходе, обозначают как А2, а переход как А1→ А2
Обычно первым записывают высокоэнергетическое состояние, поэтому переход обозначают 1А2→ 1А1 или 1А2 (n, π*) → 1А1
Слайд 42Интенсивность электронных переходов.
Сила осциллятора
υ – волновое число (см-1)
-
интегральная интенсивность, которая измеряется площадью полосы поглощения.
Полосы поглощения в
электронном спектре характеризуются:
длиной волны – для данного электронного перехода, соответствует энергии этого перехода
интенсивностью поглощения - определяется вероятностью перехода.
В электронной спектроскопии интенсивность полос поглощения измеряется обычно значением молярного коэффициента поглощения в максимуме полосы (εmax и lgεmax). Полосы поглощения также могут быть охарактеризованы силой осциллятора интегральной интенсивности.
Слайд 43Величина f
безразмерная
для полностью разрешенного перехода f = 1
Интенсивность
электронных переходов в спектрах поглощения меняется в пределах 10 порядков,
т.е.
ε – от 105 - 10-5, а f - от 1 до 10-9
Для удобства иногда используют их десятичные логарифмы:
lgε ~ от 5 до -5, lgf ~ от 0 до -9.
Для единственного симметричного пика:
f = (4,6·10-9)εmaxΔν1/2
Δν1/2 – полуширина полосы на ее полувысоте, т.е. ширина при εmax /2
εmax – молярный коэффициент экстинкции в максимуме полосы поглощения.
Слайд 44
Сила осциллятора может быть вычислена по формуле:
- вероятность перехода между двумя состояниями
m и n
Мmn – момент перехода, характеризующий изменение дипольного момента во время перехода;
m – масса электрона;
с – скорость света;
h – постоянная Планка.
Слайд 45 Момент перехода связан с волновыми функциями начального и конечного состояний
соотношением:
- интеграл момента перехода;
ψm – волновая
функция начального состояния (основного)
ψn – волновая функция конечного состояния (возбужденного)
- оператор электрического дипольного момента.
- векторная величина, поэтому ее можно разложить на компоненты x, y, z. Тогда компонентами интеграла момента перехода являются:
Если хотя бы один из этих интегралов не равен нулю, то f ≠ 0 и переход разрешен. Полосы поглощения, отвечающие разрешенным переходам, имеют f = 1 – 0,1; lgε ≥ 4. Если все интегралы равны нулю, то f = 0 и переход запрещен и согласно приближенной теории вообще не должен реализоваться, но переходы наблюдаются, так как более точные теории, учитывающие спин-орбитальное и вибронное взаимодействия, дают для этих интегралов хотя и небольшие, но отличные от нуля значения
не обращается в ноль
только в том случае, если подынтегральное выражение полносимметрично, а для этого необходимо, чтобы прямое произведение типов симметрии ψm × ψn совпадало с типом симметрии
(i = x, y, z)
ψm ×
× ψn = полносимметричный тип точечной группы, к которой принадлежит молекула
Слайд 47 Разберем на примере электронных переходов в формальдегиде.
1) π→π* переход.
Волновая функция возбужденного состояния может быть представлена прямым произведением:
Ψ =
a12 · b11 · a12 · b22 · b11 = А1
Таким образом, переход из основного в возбужденное состояния обозначается как А1 → А1
Компоненты , , преобразуются как векторы х, y, z точечной группы. Из таблицы характеров точечной группы С2v следует, что вектор дипольного момента , лежащий вдоль оси z, представляет собой А1
А1 × А1 × А1 = А1 – переход разрешен
Слайд 48 2) n → π*
А1 → А2. Из
таблицы характеров видно, что ни одна из компонент дипольного момента
не имеет симметрии А2. Следовательно, не одно из трех подынтегральных выражений не может быть равно А1 и переход запрещен, т.е. тройное произведение ψm ×
× ψn не будет полносимметричным,
только прямое произведение А2× А2 является единственным произведением, которое равно А1
А1 × А2 = А2
Слайд 49Правила отбора электронных переходов
1. По мультиплетности. Запрещены переходы между состояниями
различной мультиплетности.
2. По симметрии. Для молекул, имеющих центр симметрии, разрешенными
переходами являются u → g или g → u, а переходы u → u или g → g запрещены, т.е. запрещены переходы между состояниями с одинаковой четностью.
Переходы в молекулах, не имеющих центра инверсии, зависят от симметрии начального и конечного состояния. Если прямым произведением ψm × × ψn является А1 переход разрешен.
3. Запрещены переходы, в которых происходит возбуждение более чем одного электрона.
Слайд 50 Перечисленные правила отбора выведены из рассмотрения только электронных волновых функций,
без учета колебательных и вращательных волновых функций, без учета спин-орбитального
и спин-спинового взаимодействия. В реальных молекулах запрещенные переходы проявляются в спектрах в виде полос с малой интенсивностью (f < 0,01).
Слайд 51Хромофоры и ауксохромы
Поглощение вещества в ближнем УФ и видимой области
связано с возбуждением π→π* или n→π* переходов. Эти переходы реализуются
только в молекулах, содержащих ненасыщенные группировки.
Функциональную группу, включающую хотя бы одну кратную связь, которая придает соединению способность к избирательному поглощению в ближнем УФ или видимой области называют хромофором.
Хромофоры разделяют на изолированные и сопряженные. К первым относят группировки с одной кратной связью, такие как C=C, C=O, N=N и т.п., а ко вторым – структурные элементы, представляющие собой системы сопряженных кратных связей.
Функциональную группу, не содержащую кратных связей, которая не имеет максимума поглощения в ближнем УФ, но включение которой в систему приводит к увеличению длины волны π→π* перехода и увеличению интенсивности поглощения, называют ауксохромом. Типичными ауксохромами являются OH-, NH2-, SH-группы, т.е. группы, содержащие гетероатом со свободной электронной парой.
Слайд 521. Очень интенсивные полосы с ε > 103 соответствующие π→π*
переходам, типичные для конъюгированных (сопряженных) систем, обозначаются как К-полосы. Аналогичные
по интенсивности полосы π→π* переходов в ароматических системах обозначаются как Е-полосы (Е1 соответствуют разрешенным по симметрии переходам ε ~ 104 – 105, а Е2 – запрещенным переходам с ε ~ 2000 – 12000)
2. Слабые полосы n→π* переходов c ε < 102, характерные для непредельных гетероатомных функциональных групп и радикалов – R-полосы.
3. Полосы средней интенсивности (ε ~ 102 – 103), соответствующие запрещенным π→π* переходам в ароматических структурах бензольного типа – В – полосы.
Слайд 53 Замещение или изменение структуры органический соединений вызывает изменение длины волны
и интенсивности полосы поглощения.
Смещения полос поглощения в сторону длинных
волн носят названия батахромных смещений, а смещения в коротковолновую область называют гипсохромными смещениями.
Гиперхромным эффектом называется увеличение интенсивности полос поглощения, а гипохромным эффектом – уменьшение интенсивности.
Слайд 54Влияние растворителя на электронные спектры веществ
Структура и положение полос поглощения
зависят от природы растворителя. Полярные растворители, как правило, изменяют положение
полос поглощения и упрощают их колебательную структуру. Неполярные растворители не вызывают столь значительных изменений в структуре по сравнению с полосами веществ в газовой фазе.
Различным является влияние растворителя на n→π* и π→π* переходы.
В растворителях с высокой диэлектрической проницаемостью или способных к образованию сильных водородных связей наблюдается сдвиг полос поглощения n→π* переходов в синюю область (гипсохромный сдвиг), а для полос поглощения, соответствующих π→π* переходам - в сторону более длинных волн (красное или батахромное смещение). При этом колебательная структура π→π* полос сохраняется даже в полярных растворителях
Слайд 56 Замена полярного растворителя на инертный позволяет установить некоторые структурные особенности
органических молекул. В частности, такая замена уместна при установлении относительного
расположения функциональных групп, способных к образованию водородных связей (например, ОН- и С=О), поскольку позволяет выявить структуры с внутримолекулярной водородной связью.
Слайд 57 Замена растворителя может привести к изменению таутомерного равновесия. При этом
если таутомеры содержат разные хромофоры, то замена растворителя вызовет сильное
изменение параметров спектра.
УФ спектры ацетоуксусного эфира в изооктане (1) и в воде (2)
Слайд 58 Использование в качестве растворителе спиртовых и водных растворов кислот
и щелочей часто оказывается полезным для структурного отнесения в ряду
соединений, способных участвовать в кислотно-основном равновесии с указанными растворителями. Так, в ряду окси и аминопроизводных углеводородов возможно легко выявить фенолы и анилины, наблюдая изменения в спектре при замене инертного растворителя на щелочной (для оксипроизводных) или кислотный (для аминопроизводных) растворитель.
УФ спектры фенола и анилина:
а) 1 – фенол в воде; 2 – в водном
0.1 М растворе NaOH
б) 1 – анилин в воде; 2 - в водном
0.1 М растворе НСl
Слайд 59 Для обнаружения хромофоров, содержащих основный азот (например хромофор С=N в
алифатических азометинах) снимают спектр в кислотном растворителе: спектр заметно меняется,
так как вследствие протонирования азота полоса n→π* исчезает.
УФ – спектры пиридина в спирте (1)
и подкисленном спирте (2)
Слайд 60Электронные спектры поглощения отдельных классов органических соединений
Насыщенные соединения
В насыщенных углеводородах
(парафинах и циклопарафинах), содержащие простые связи, возможны только переходы σ→σ*.
Полосы соответствующие этим переходам лежат в области вакуумного ультрафиолета.
В спектрах насыщенных молекул, содержащих гетероатом с неподеленными электронными парами, длинноволновая полоса относится к переходу n→σ*.
Слайд 61 Ненасыщенные соединения
Непредельные углеводороды с изолированными двойными связями имеют интенсивную полосу
поглощения, обусловленную π→π* переходом, в области 165-200 нм. Алкильные заместители
у этиленовых углеродных атомов приводят к смещению полосы перехода π→π* в длинноволновую сторону, и соответствующее поглощение наблюдается при 175 – 200 нм. Циклические непредельные углеводороды и ацетиленовые углеводороды с изолированной С ≡ С - связью имеют спектры, аналогичные спектрам алкенов.
Сопряжение двойных связей вызывает смещение полос поглощения в длинноволновую область с увеличением интенсивности. Спектры большинства полиенов характеризуются колебательной структурой на основной полосе поглощения.
Циклические диены поглощают при более длинных волнах, чем линейные, но интенсивность у них меньше.
В спектрах полиинов, кроме полосы средней интенсивности (340 – 390 нм), появляются полосы высокой интенсивности (ε > 100000) в области 200 – 280 нм, также имеющие колебательную структуру.
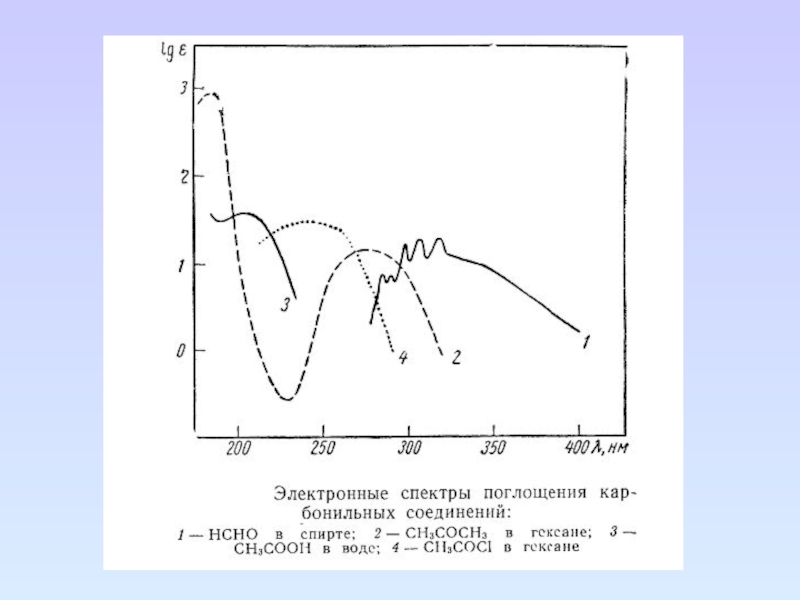
Слайд 65 Карбонильные соединения
Карбонильные соединения содержат гетероатомы, связанные кратной связью, в таких
группах возможны три типа электронных переходов:
π→π*, n→π*, n→σ*.
В спектре формальдегида
имеются три полосы поглощения, максимумы которых находятся при 295, 185, 155 нм. Эти полосы соответственно относятся к n→π*, n→σ*, π→π*. Коротковолновая полоса является наиболее интенсивной. Полоса перехода n→π* запрещена по симметрии и отличается невысокой интенсивностью (ε295 = 10).
При переходе от формальдегида к ацетальдегиду и ацетону наблюдается гипсохромное смещение полосы n→π* перехода.
Замещение водород альдегидной группы на OR, NR2, Hal сопровождается сильными гипсохромными сдвигами n→π* полосы.
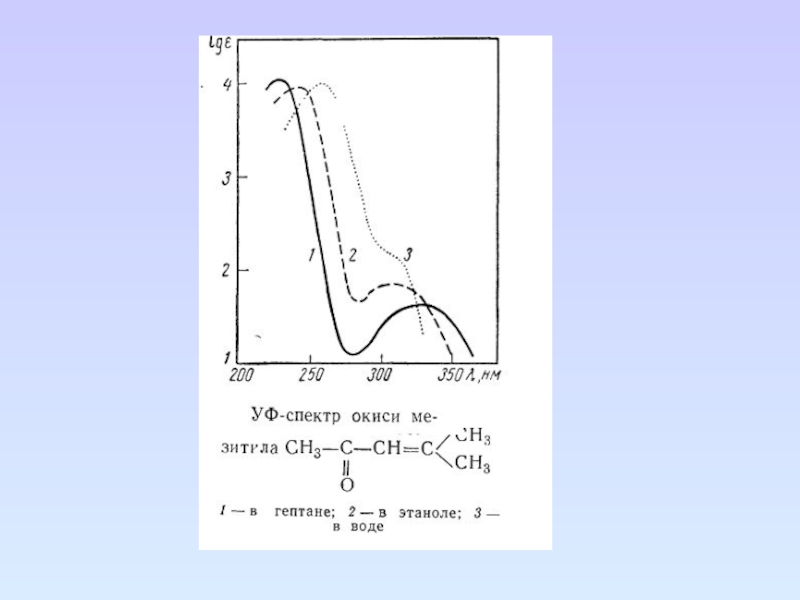
Слайд 68 Непредельные карбонильные соединения. Сопряжение кратной связи с карбонильной группой вызывает
длинноволновое смещение n→π*, π→π* переходов по сравнению с изолированными хромофорными
группами. α, β-ненасыщенные альдегиды и кетоны характеризуются интенсивной полосой перехода π→π* (ε ≈ 10 000) в область 220 -200 нм и низкоинтесивной (ε < 100) полосой перехода n→π* около 320 нм. В спектрах α, β-непредельных кислот и их производных также наблюдается батохромное смещение полос.
Соединения, содержащие группу C=N.
Алифатические азометины поглощают при меньших длинах волн и с большей на порядок величиной ε, чем соответствующие альдегиды и кетоны.
Например, жирные азометины типа R3C-CH=NR имеют полосу с интенсивностью lgε ≈ 2 в области 240 – 250 нм. Это полоса обладает всеми свойства полос n→π* перехода.
Связь C=N имеется в таких производных альдегидов и кетонов, как оксимы и семикарбазоны. В этих соединениях полоса перехода n→π* группы C=N не проявляется, так как спектры данных веществ содержат интенсивные полосы поглощения в области выше 230 нм, которые перекрывают полосы переходов n→π*.

Слайд 70Тиокарбонильные соединения. Тиокарбонильная группа по своему поглощению аналогична карбонильной, однако
ее полосы расположены в более длинноволновой области.
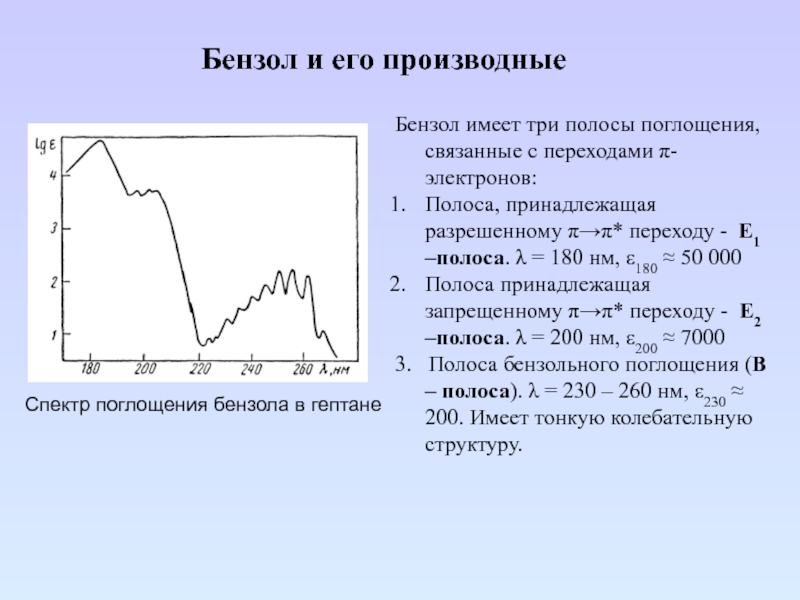
Слайд 71Бензол и его производные
Спектр поглощения бензола в гептане
Бензол имеет три
полосы поглощения, связанные с переходами π-электронов:
Полоса, принадлежащая разрешенному π→π* переходу
- Е1 –полоса. λ = 180 нм, ε180 ≈ 50 000
Полоса принадлежащая запрещенному π→π* переходу - Е2 –полоса. λ = 200 нм, ε200 ≈ 7000
3. Полоса бензольного поглощения (В – полоса). λ = 230 – 260 нм, ε230 ≈ 200. Имеет тонкую колебательную структуру.
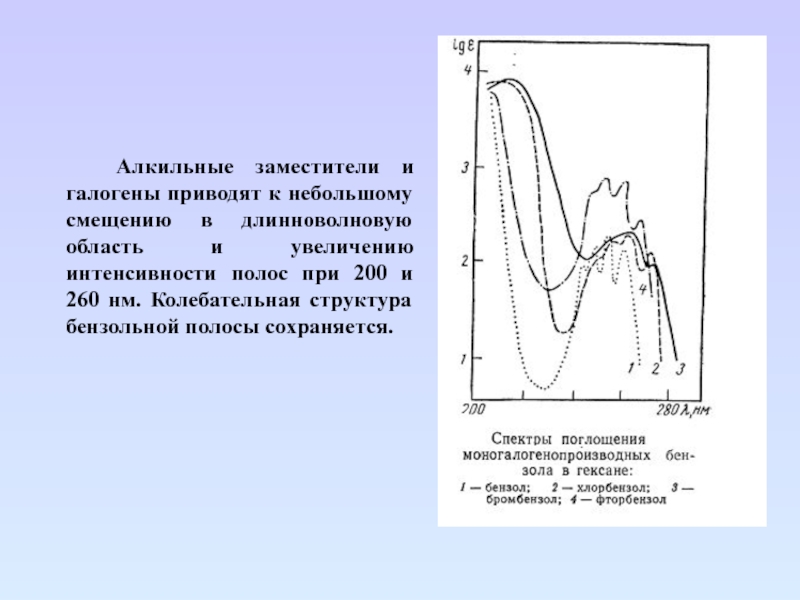
Слайд 72 Алкильные заместители и галогены приводят к небольшому смещению в длинноволновую
область и увеличению интенсивности полос при 200 и 260 нм.
Колебательная структура бензольной полосы сохраняется.
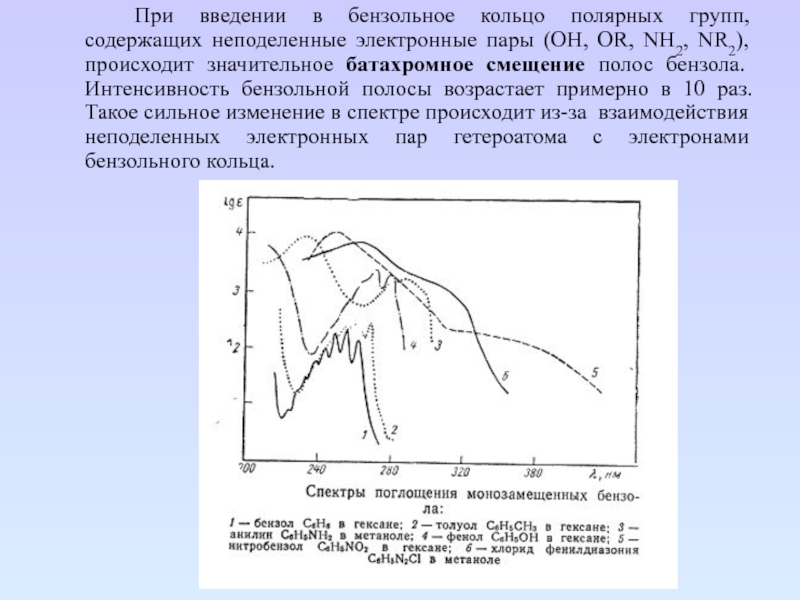
Слайд 73 При введении в бензольное кольцо полярных групп, содержащих неподеленные электронные
пары (OH, OR, NH2, NR2), происходит значительное батахромное смещение полос
бензола. Интенсивность бензольной полосы возрастает примерно в 10 раз. Такое сильное изменение в спектре происходит из-за взаимодействия неподеленных электронных пар гетероатома с электронами бензольного кольца.
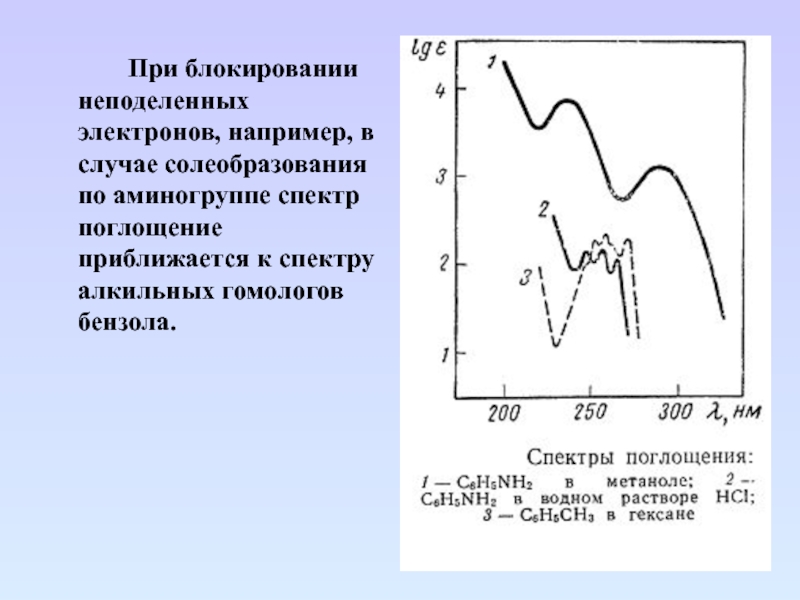
Слайд 74 При блокировании неподеленных электронов, например, в случае солеобразования по аминогруппе
спектр поглощение приближается к спектру алкильных гомологов бензола.
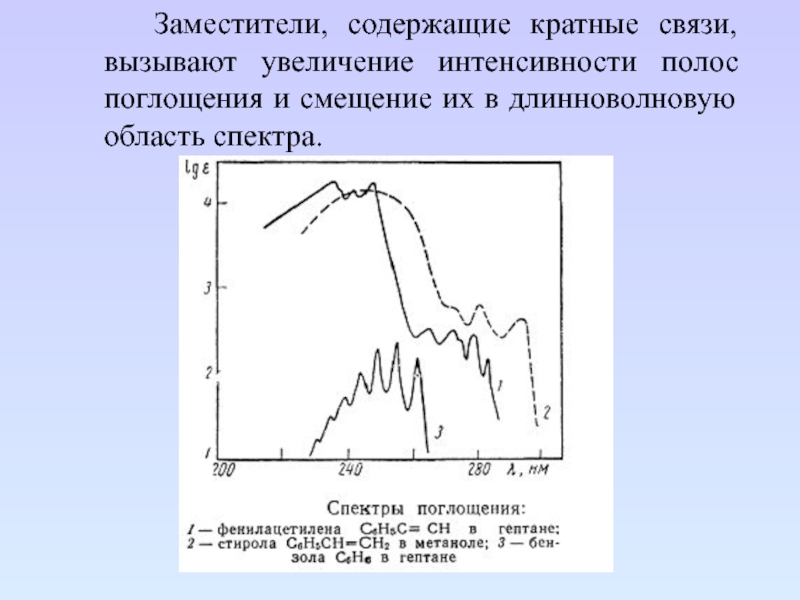
Слайд 75 Заместители, содержащие кратные связи, вызывают увеличение интенсивности полос поглощения и
смещение их в длинноволновую область спектра.
Слайд 76 Если заместителем является карбонильная группа, в спектре могут наблюдаться полосы
перехода n→π*. Они хорошо видны в спектрах неполярных растворителей, в
полярных растворителях слабые полосы n→π* перехода перекрываются полосой бензольного поглощения.
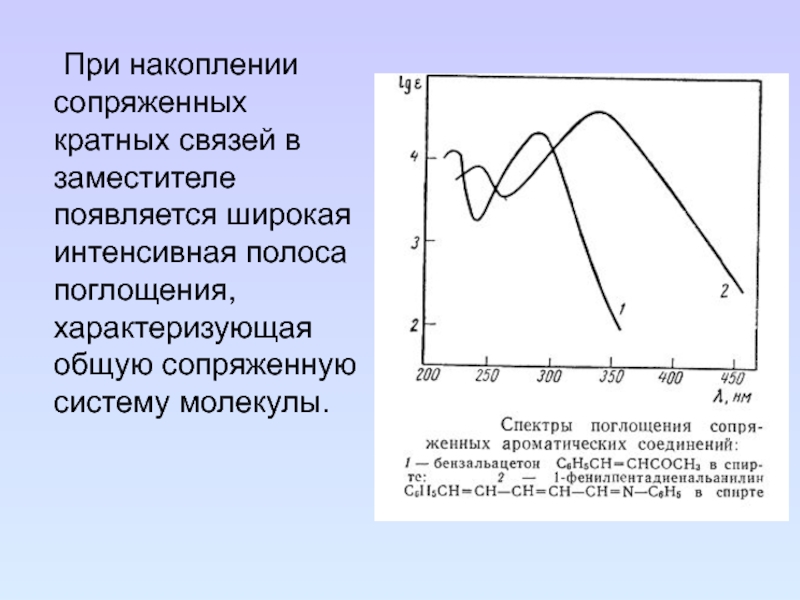
Слайд 77 При накоплении сопряженных кратных связей в заместителе появляется широкая интенсивная
полоса поглощения, характеризующая общую сопряженную систему молекулы.
Слайд 78 При наличии двух заместителей в бензольном кольце спектр соединения зависит
от природы заместителей и от их взаимного расположения. Наибольшие изменения
в спектрах дизамещенных бензолов наблюдаются для соединения, содержащих одновременно электроннодонорные и электроноакцепторные заместители, причем характер спектра зависит от их положения: орто- и мета-изомеры имеют подобные спектры, спектр пара-изомера резко от них отличается и , как правило, имеет одну интенсивную полосу поглощения.
Слайд 80Электронные спектры комплексов переходных металлов
Электронные спектры комплексов переходных металлов интерпретируют
с помощью теории кристаллического поля (ТКП)
Основные положения:
1.
Комплексное соединение моделируется центральным ионом переходного элемента, который рассматривается в базисе его d-орбиталей.
2. Центральный ион окружен точечными зарядами или диполями, характер расположения которых относительно центрального иона определяет симметрию действующего на него внешнего электростатического поля.
3. Взаимодействие между центральным ионом и лигандом носит чисто электростатический характер
Слайд 86 В зависимости величины параметра ∆ и межэлектронного взаимодействия зависит распределение
электронов по орбиталям. Увеличение параметра ∆ будет способствовать расположению электронов
на более низких орбиталях, в то время как межэлекронное отталкивание способствует равномерному распределению электронов по d-орбиталям с параллельной ориентацией спина.
d4 Cr2+ (t2g)3eg1 или (t2g)4
Mn3+
d5 Mn2+ (t2g)3eg2 или (t2g)5
Fe3+
d6 Fe2+ (t2g)4eg2 или (t2g)6
Co3+
d7 Co2+ (t2g)5eg2 или (t2g)6 (eg)1
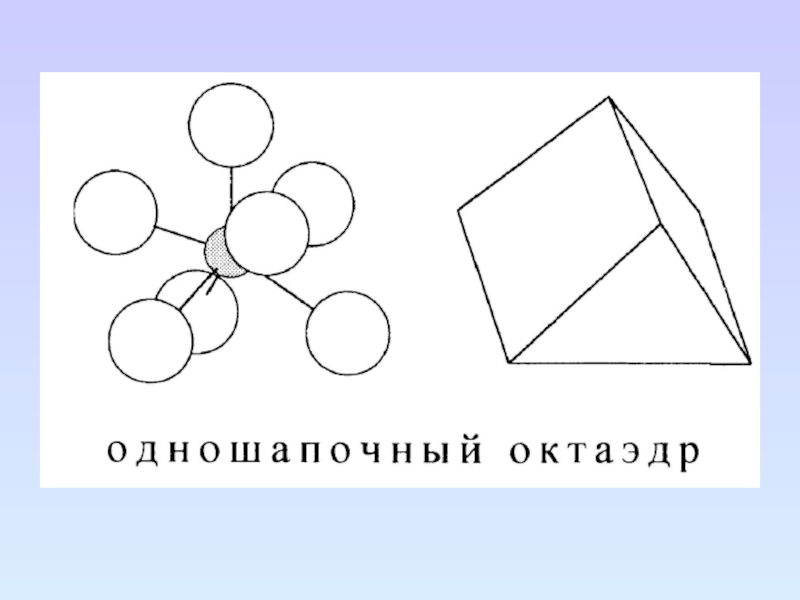
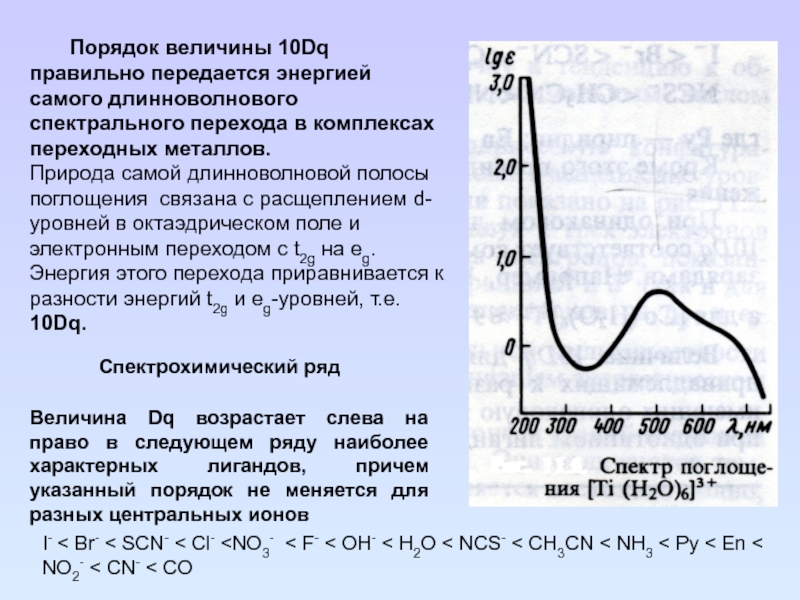
Слайд 87
Порядок величины 10Dq правильно передается энергией самого длинноволнового спектрального
перехода в комплексах переходных металлов.
Природа самой длинноволновой полосы поглощения
связана с расщеплением d-уровней в октаэдрическом поле и электронным переходом с t2g на eg. Энергия этого перехода приравнивается к разности энергий t2g и eg-уровней, т.е. 10Dq.
I- < Br- < SCN- < Cl- Спектрохимический ряд
Величина Dq возрастает слева на право в следующем ряду наиболее характерных лигандов, причем указанный порядок не меняется для разных центральных ионов
Слайд 88Расщепление энергетических состояний для dn-конфигураций центральных ионов
Определенное энергетическое состояние атома
называют атомным термом.
Любое обозначение терма группирует вместе все вырожденные
размещения в ионе.
Терм обозначают 2S+1LJ
2S+1 – мультиплетность
L – полное орбитальное квантовое число
J – квантовое число полного углового момента, изменяется от L+S до L-S
- число возможных значений J
Слайд 89 В октаэдрическом и тетраэдрическом, а также кубических электростатических полях лигандов
термы центрального иона независимо от мультиплетности расщепляются следующим образом:
S→A1(1)
P→T1(3)
D→E(2)+T2(3)
F→A2(1)+T1(3)+T2(3)
G→A1(1)+E(2)+T1(3)+T2(3)
Слайд 91Диаграммы Оргела
Диаграмма Оргела для высокоспиновых d1, d9,
d4, d6 - комплексов
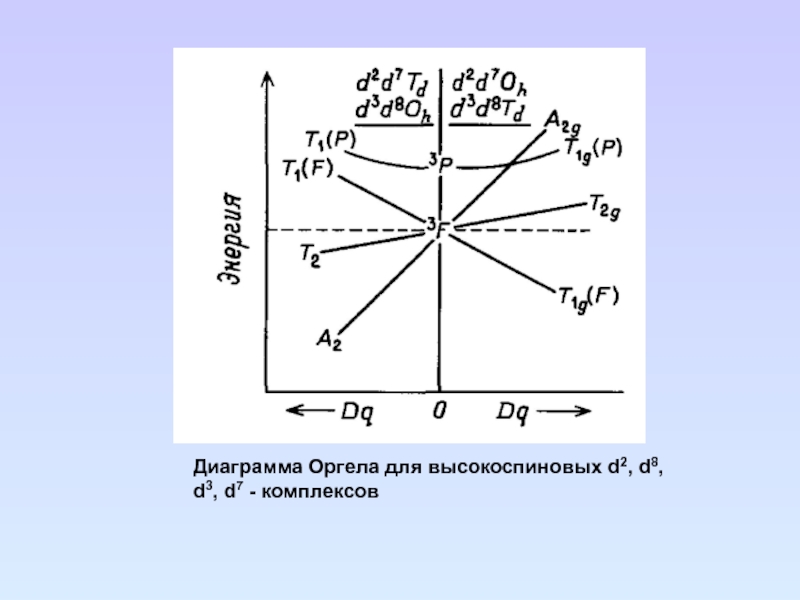
Слайд 92Диаграмма Оргела для высокоспиновых d2, d8,
d3, d7 - комплексов
Слайд 96Нефелоуксетический ряд
F->H2O>urea>NH3>
en~C2O42-> NCS-> Cl-~CN-
>Br-> S2- ~I-.
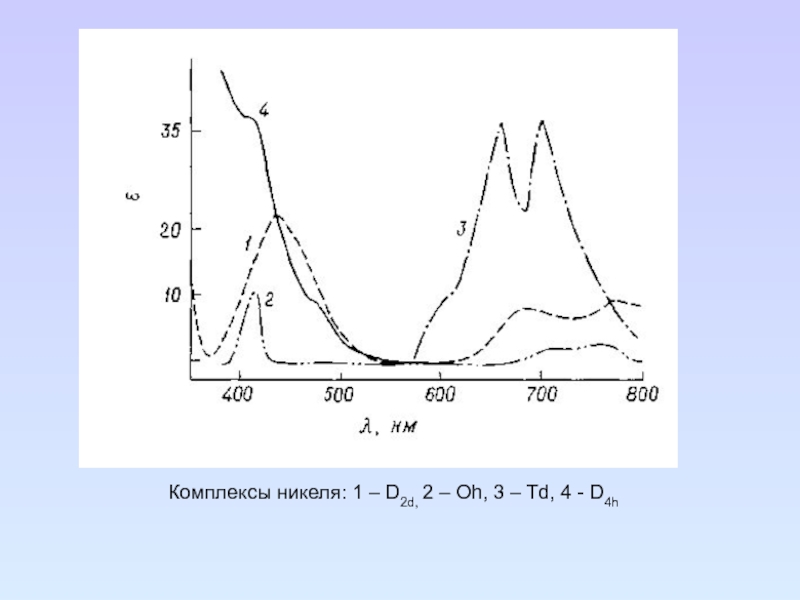
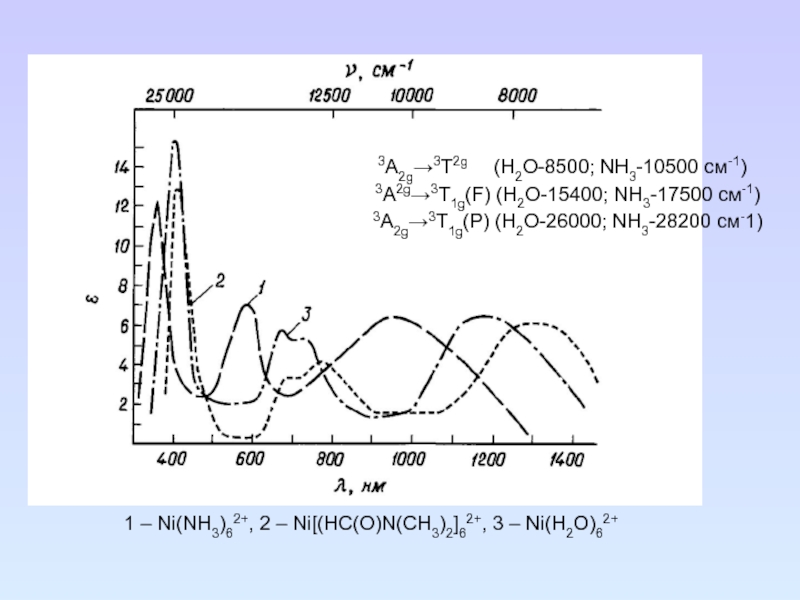
Слайд 983А2g→3T2g (H2O-8500; NH3-10500 см-1)
3А2g→3T1g(F) (H2O-15400; NH3-17500 см-1)
3А2g→3T1g(P) (H2O-26000; NH3-28200 см-1)
1 – Ni(NH3)62+, 2 – Ni[(HC(O)N(CH3)2]62+,
3 – Ni(H2O)62+
Слайд 99Уравнения Танабе – Сугано для Ni2+ в
октаэдрическом поле
E (3Т2g)
= -2Dq
E (3A2g) = -12Dq
E (3T1g(F)) и E (3T1g(P)):
[6DqP
– 16(Dq)2] + [-6Dq – p]E + E2 = 0
P – энергия состояния 3Р
P = 15 B, B – параметр Рака
Параметр Рака указывает на величину межэлектронного
отталкивания между различными уровнями в газообразном
ионе.
Слайд 100Построение диаграммы Оргела
1. Энергию основного состояния центрального иона (энергию терма)
принимаем за ноль.
2. Находим разность между энергиями термов.
3. Энергии термов
откладываем на оси ординат диаграммы.
4. По таблицам находим параметр Рака для центрального иона в свободном состоянии.
5. Вычисляем по уравнениям энергии компонент расщепления терма.
6. Полученные значения энергий наносим на диаграмму и соединяем точки.
Слайд 101Построение диаграммы Оргела для октаэдрических комплексов Ni2+
Энергию основного состояния Ni2+
т.е энергию терма 3F, принимаем за ноль расчета.
Для конфигурации d6
существуют термы 3F и 3P. Относительная энергия их в параметрах Рака равна:
3F – (3А-15В)
3P - 3А
Находим разность между энергиями термов: 3P - 3F = 3А – 3А + 15В = 15В.
Энергии термов 3F и 3P откладываем на оси ординат диаграммы.
По таблицам находим параметр Рака для свободного иона Ni2+ (он равен 1056).
Слайд 102Вычисляем по уравнениям энергии компонент расщепления терма 3F: 3A2g, 3T2g,
3T1g , а также энергию 3T1g (3P) в поле лигандов.
Так,
Е(A2g) = -12Dq
Е(3T2g) = -2Dq
а энергии термов 3T1g (3F), 3T1g (3P) получаем как корни квадратного уравнения
E2 – (6Dq + P)E + (6DqP – 16(Dq)2) = 0,
где Р – энергия терма 3P для свободного иона Ni2+.
Полученные значения энергий наносим на диаграмму и соединяем точки.
Слайд 108Комплексы никеля: 1 – D2d, 2 – Oh, 3 –
Td, 4 - D4h
Слайд 109Методы определения электрических дипольных моментов молекул
Диэлектрическая проницаемость и электрическая
поляризация диэлектрика. Дипольный момент молекулы
Диэлектрики - вещества, которые не
проводят электрического тока. Молекулы диэлектрика электрически нейтральны и содержат равное число положительных и отрицательных зарядов. Тем не менее, молекулы обладают электрическими свойствами. В первом приближении молекулу диэлектрика можно рассматривать как диполь, имеющий дипольный электрический момент:
(1)
где q – абсолютная величина суммарного положительного, а также суммарного отрицательного зарядов, расположенных, соответственно, в центрах тяжести этих зарядов; l –вектор, направленный от центра тяжести положительных зарядов к центру тяжести отрицательных (расстояние между этими центрами).
В СИ единицей величины электрического дипольного момента является Кл.м; внесистемная единица – дебай D (1D = 3,34 . 10-30 Кл . м).
Слайд 110Полярным диэлектриком называется такой диэлектрик, молекулы (атомы) которого имеют электроны,
расположенные несимметрично относительно своих ядер (H2O, HCl, NH3, CH3Cl и
др.). В таких молекулах центры тяжести положительных и отрицательных зарядов не совпадают, находясь, практически, на постоянном расстоянии l друг от друга. Молекулы полярных диэлектриков по своим электрическим свойствам подобны жестким диполям, у которых имеется постоянный дипольный момент: µ = const.
Различный характер распределения электрического заряда позволяет разделить все диэлектрики на два класса – неполярные и полярные.
Диэлектрик называется неполярным, если электроны атомов в его молекулах расположены симметрично относительно ядер (H2, O2, CCl4 и др.). В таких молекулах центры тяжести положительных и отрицательных зарядов совпадают в отсутствие внешнего электрического поля (l = 0) и дипольный момент молекулы равен нулю.
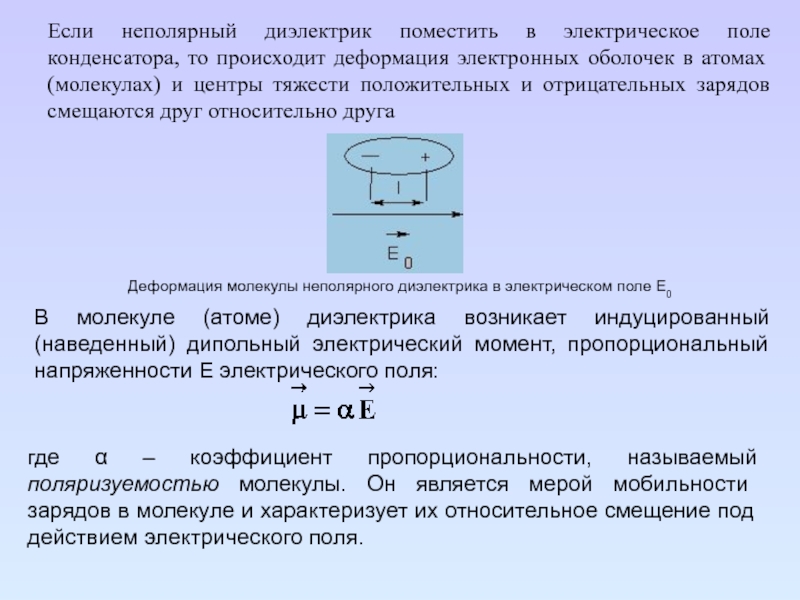
Слайд 111Если неполярный диэлектрик поместить в электрическое поле конденсатора, то происходит
деформация электронных оболочек в атомах (молекулах) и центры тяжести положительных
и отрицательных зарядов смещаются друг относительно друга
Деформация молекулы неполярного диэлектрика в электрическом поле Е0
В молекуле (атоме) диэлектрика возникает индуцированный (наведенный) дипольный электрический момент, пропорциональный напряженности Е электрического поля:
где α – коэффициент пропорциональности, называемый поляризуемостью молекулы. Он является мерой мобильности зарядов в молекуле и характеризует их относительное смещение под действием электрического поля.
Слайд 112В полярных диэлектриках молекулы представляют собой электрические диполи, которые в
отсутствии электрического поля ориентированы хаотически (суммарный дипольный момент всех молекул
равен нулю), но под действием поля эти диполи ориентируются вдоль него. Помимо ориентации диполей вдоль электрического поля происходит деформация молекул, и в них создается некоторый индуцированный дипольный момент.
Ориентация молекулы полярного диэлектрика в электрическом поле
Слайд 113Заполнение пространства между пластинами конденсатора диэлектриком приводит к уменьшению напряженности
поля в ε раз.
εs = Е0/Е
где Е0 – напряженность поля в вакууме; Е0 = 4πq (q – поверхностная плотность зарядов на пластинах конденсатора).
Е – напряженность поля конденсатора с диэлектриком.
εs – статическая диэлектрическая проницаемость, которая показывает во сколько раз в данной среде сила взаимодействия между зарядами уменьшается по сравнению с вакуумом. Величину статической диэлектрической проницаемости определяют путем измерения емкости:
εs = с/с0
где С0 и С – емкости конденсатора в вакууме и с диэлектриком соответственно
Слайд 114Уменьшение напряженности электрического поля в конденсаторе вызвано поляризацией диэлектрика, т.е.
накоплением отрицательных зарядов вблизи положительно заряженной пластины и положительных зарядов
вблизи отрицательной пластины конденсатора, что приводит к уменьшению первоначальных зарядов q. В объеме диэлектрика индуцированные заряды компенсируются.
Макроскопическое описание изменения разности потенциалов при введении диэлектрика между пластинами плоскопараллельного конденсатора
Слайд 115Смещение зарядов под действием поля называется электрической поляризацией вещества Р.
Если в единице объема (1см3) содержится n молекул, обладающих индуцированным
дипольным моментом, то поляризация Р будет равна
Связь статической диэлектрической проницаемости с поляризуемостью молекулы и числом молекул в единице объема, т.е. плотностью вещества выражается формулой Клаузиуса-Моссотти:
где Р – молярная поляризация;
N – число Авагадро,
M – молекулярный вес
d – плотность вещества
Формула Клаузиуса-Моссотти строго применима только к неполярным газам. Она также может быть приближенно справедлива для полярных газов при низких давлениях, и для неполярных жидкостей если пренебречь короткодействующим взаимодействием между молекулами. Она не применима для полярных жидкостей, когда взаимодействием дипольных молекул на близких расстояниях создают значительные внутренние поля.
Слайд 116Основные виды поляризации диэлектрика
Молекулярная поляризация P может быть представлена
в виде суммы электронной Рэ, атомной Ра и ориентационной Рор
поляризаций
Р = Рэ + Ра + Рор
Каждый из указанных видов поляризации характеризуется определенным типом смещения зарядов частиц диэлектрика под действием приложенного поля.
Сумма электронной Рэ и атомной Ра поляризаций называется деформационной поляризацией Рд.
Слайд 117Электронная поляризация характеризуются упругим смещением электронных орбиталей относительно ядра при
воздействии на атом (молекулу) электрического поля определенной напряженности. Она имеет
место во всех атомах или молекулах как полярных, так и неполярных диэлектриков, независимо от возможности возникновения в диэлектрике других видов поляризации.
Время установления электронной поляризуемости в молекуле под действием электрического поля сравнимо с периодом световых колебаний (10-14 – 10-16 сек). Поэтому к неполярным диэлектрикам, молекулы которых в электрическом поле обладают только электронной поляризуемостью, применяют соотношение
n2 = εs
где n – показатель преломления
Подставляя в формулу Клаузиуса-Моссотти вместо статической диэлектрической проницаемости значение квадрата показателя преломления, определенного при бесконечной длине волны, получаем формулу Лорентца-Лоренца, описывающую оптическое поведение вещества
где R∞ - молекулярная рефракция
Слайд 118Атомная поляризация – вид поляризации, когда в электрическом поле смещаются
не только электронные облака, но и сами ядра атомов.
Время установления
атомной поляризуемости αа совпадает с периодом колебаний в инфракрасной области спектра. Причиной этого является то, что колебания атомных ядер из-за их малой частоты не могут быть возбуждены видимым светом, а возбуждаются только инфракрасным.
Атомная поляризация Ра достаточно мала по сравнению с электронной поляризацией Рэ, составляет примерно 10% от последней.
Сумма электронной и атомной поляризаций представляет собой деформационную поляризацию характеризующую упругое смещение, как электронных облаков, так и ядер атомов в молекуле при воздействии электрического поля.
Слайд 119В случае полярных молекул наряду с деформационной поляризуемостью существует еще
один вид поляризуемости, вызванной ориентацией постоянных диполей в электрическом поле.
Этот вид поляризуемости называют ориентационной поляризуемостью, а соответствующую ей поляризацию – ориентационной поляризацией Рор. Процесс установления ориентационной поляризации протекает еще боле медленнее, чем атомной и соответствует периоду радиоволн.
Связь между постоянным дипольным моментом μ0 и ориентационной поляризуемостью αор полярной молекулы может быть выражена соотношением
Слайд 120Общим выражением для поляризуемости молекул является соотношение:
Подставляя значение общей поляризуемости
молекул в уравнение Клаузиуса-Моссотти, получим формулу Дебая, устанавливающую зависимость диэлектрической
проницаемости полярных диэлектриков не только от поляризуемости молекул, но и от величины постоянного дипольного момента и ориентации его в электрическом поле:
На формулу Дебая распространяются все ограничения, присущие уравнению Клаузиуса-Моссотти, т.е. она применима к полярным газам при очень низких давлениях, а также к предельно разбавленным растворам полярных веществ в неполярных растворителях. Она неприменима к полярным жидкостям, так как не учитывает внутреннее поле, создаваемое в жидком полярном диэлектрике.
Слайд 121Определение дипольных моментов в разбавленных растворах вторым методом Дебая)
Основные допущения
данного метода:
а) В предельно разбавленных растворах молекулы полярного вещества должны
вести себя также как и в парообразном состоянии, и должны свободно ориентироваться в приложенном поле.
б) Метод основан на том, что общая поляризация обладает свойством аддитивности:
где Рр-ра, Рр-ля, Рв-ва - молярные поляризации раствора, растворителя и растворенного вещества соответственно;
Nр-ля, Nв-ва – мольные доли растворителя и растворенного вещества.
Слайд 122Исходя из уравнения Клаузиуса-Моссотти поляризации растворителя и растворенного вещества равны:
Следовательно,
молярная поляризация раствора равна следующему выражению:
где Mр-ля, Mв-ва – молекулярные
веса растворителя и растворенного вещества,
dр-ра – плотность раствора
Слайд 123Зная величину Рв-ва∞ можно определить значение ориентационной поляризации растворенного вещества
Рэ = R, Pa = 0,1R
[D]
Экстраполяция поляризации Рв-ва к бесконечному разбавлению не является точной вследствие криволинейности Рв-ва = f(Nв-ва). Поэтому для уменьшения ошибок был предложен ряд экстраполяционных формул, среди которых наиболее применяемым являются формулы предложеныые Гедестрандом.
Слайд 124Определение дипольного момента молекулы методом Гедестранда
В данном методе вместо
поляризации растворенного вещества к нулевой концентрации экстраполируют (Nв-ва→ 0) диэлектрическую
проницаемость (εр-ра) и плотность (dр-ра) растворов, которые в большинстве случаев являются линейными функциями концентрации в мольных долях растворенного вещества:
ε = εр-ля(1+αNв-ва)
d = dр-ля(1+βNв-ва)
где εр-ля, dр-ля – диэлектрическая проницаемость и плотность растворителя;
α, β – коэффициенты, характеризующих наклон кривых, полученных из зависимости ε и d от мольной доли растворенного вещества.
Коэффициенты α и β из данных для нескольких растворов проводят методом наименьших квадратов.
Из этих соотношений Гедестранд получил следующее уравнение для поляризации растворенного вещества при бесконечном растворении
Уравнение Гедестранда неприменимо, если нет линейной зависимости диэлектрической проницаемости и плотности растворенного вещества, что часто наблюдается в концентрированных растворах.
























































































![Электронная спектроскопия [Co(H2O)6]2+ [CoCl4]2+ [Co(H2O)6]2+ [CoCl4]2+](/img/thumbs/5ad80d07c9eae2b3dc7cce0b32ebd19e-800x.jpg)