Элементы мат.статистики и теории вероятности Упражнение О.3 Упражнение

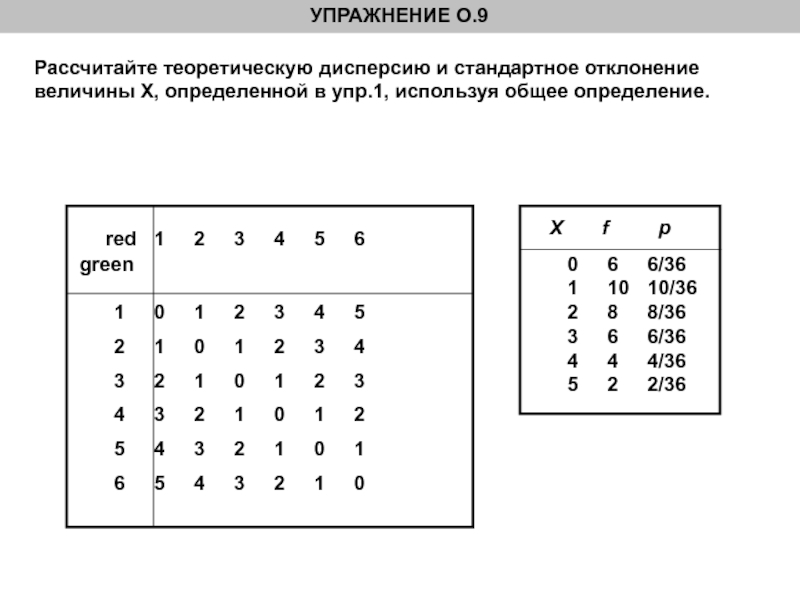
О.9
Упражнение О.19
Упражнение О.18
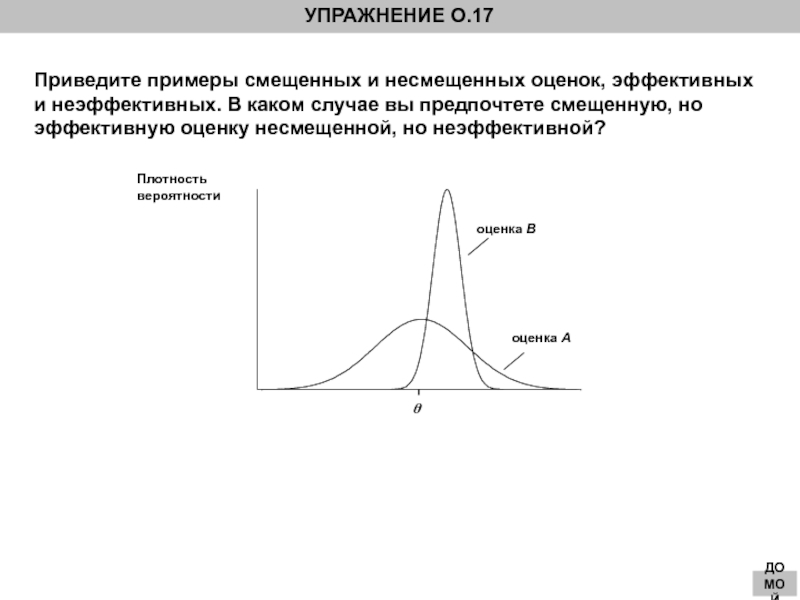
Упражнение О.17
Упражнение О.6
Упражнение О.14
Упражнение О.13
Упражнение О.5
Упражнение О.4
Упражнение О.12
Упражнение

О.22

Упражнение О.21

Упражнение О.20

Упражнение О.8

Упражнение О.16

Упражнение О.15

Упражнение О.7

14 15 16 17 18 20 21

1 3 6 9 5 8

По материалам курса C.Dougherty “Introduction to Econometrics” (London School of Economics)
См. учебник К. Доугерти «Введение в эконометрику», 2009.

числами, выпавшими при бросании двух костей. Если они равны между

собой, то X считается равной нулю. Найти распределение вероятностей для X.

УПРАЖНЕНИЕ О.1

при бросании двух костей, или любому из выпавших чисел, если

они одинаковы. Найти распределение вероятностей для X.

УПРАЖНЕНИЕ О.2

red 1 2 3 4 5 6
green
1 0 1 2 3 4 5
2 1 0 1 2 3 4
3 2 1 0 1 2 3
4 3 2 1 0 1 2
5 4 3 2 1 0 1
6 5 4 3 2 1 0
УПРАЖНЕНИЕ О.3

red 1 2 3 4 5 6
green
1 1 2 3 4 5 6
2 2 2 3 4 5 6
3 3 3 3 4 5 6
4 4 4 4 4 5 6
5 5 5 5 5 5 6
6 6 6 6 6 6 6
УПРАЖНЕНИЕ О.4

l - константа, докажите, что математическое ожидание lX равно lmX.

УПРАЖНЕНИЕ О.5

red 1 2 3 4 5 6
green
1 0 1 2 3 4 5
2 1 0 1 2 3 4
3 2 1 0 1 2 3
4 3 2 1 0 1 2
5 4 3 2 1 0 1
6 5 4 3 2 1 0
УПРАЖНЕНИЕ О.6

red 1 2 3 4 5 6
green
1 1 2 3 4 5 6
2 2 2 3 4 5 6
3 3 3 3 4 5 6
4 4 4 4 4 5 6
5 5 5 5 5 5 6
6 6 6 6 6 6 6
УПРАЖНЕНИЕ О.7

костей. Рассчитайте возможные значения величины Y, определенной как

Y = 2X + 3
и ее математическое ожидание E(Y). Покажите, что оно равно 2E(X) + 3.

УПРАЖНЕНИЕ О.8

упр.1, используя общее определение.

red 1 2 3 4 5 6
green
1 0 1 2 3 4 5
2 1 0 1 2 3 4
3 2 1 0 1 2 3
4 3 2 1 0 1 2
5 4 3 2 1 0 1
6 5 4 3 2 1 0
УПРАЖНЕНИЕ О.9

упр.2, используя общее определение.

red 1 2 3 4 5 6
green
1 1 2 3 4 5 6
2 2 2 3 4 5 6
3 3 3 3 4 5 6
4 4 4 4 4 5 6
5 5 5 5 5 5 6
6 6 6 6 6 6 6
УПРАЖНЕНИЕ О.10

по формуле



совпадает с результатом, полученным в упр. 9 (используйте результаты

упражнений 3 и 6).

УПРАЖНЕНИЕ О.11

по формуле



совпадает с результатом, полученным в упр. 10 (используйте результаты

упражнений 4 и 7).

УПРАЖНЕНИЕ О.12

измеренной по Фаренгейту, F. Покажите, что значение коэффициента корреляции не

изменится, если температуру измерять в шкале Цельсия, C.
Замечание: C = 5/9 (F – 32).

УПРАЖНЕНИЕ О.13

l + mX
где l и m - константы. Покажите, что

коэффициент корреляции между X и Y равен 1 или –1, в зависимости от знака m.

УПРАЖНЕНИЕ О.14

из n значений. Покажите, что выборочное среднее



является несмещенной оценкой теоретического

среднего

из n значений. Покажите, что взвешенное среднее этих значений



будет несмещенной

оценкой теоретического среднего, если сумма весов равна 1

В каком случае вы предпочтете смещенную, но эффективную оценку несмещенной,

но неэффективной?

ДОМОЙ

дисперсией σХ .
Пусть в выборке имеются всего два наблюдения х1

и х2. Покажите, что оценка среднего


будет наиболее эффективной среди всех несмещенных оценок, если λ1 =λ2 =1/2

УПРАЖНЕНИЕ О.18

Верно ли утверждать, что оценка становится более эффективной?


УПРАЖНЕНИЕ О.19

Верно ли, что оценка становится более эффективной?


ДОМОЙ
Нет, не верно.
Когда размер

выборки увеличивается, дисперсия оценки уменьшается, и как следствие, скорее всего получится более точный результат оценки теоретических значений. Поскольку наша оценка улучшается в этом смысле, ее хочется назвать более эффективной, но это неверное использование термина «эффективность».
«Эффективность» - это понятие, которое используется для сравнения двух или более альтернативных оценок (способов оценивания), определяемых по одной и той же выборке из одних и тех же данных. Та оценка, которая имеет наименьшую дисперсию, называется более эффективной.
Утверждать, что с увеличением выборки оценка становится более эффективной, нельзя, потому что в этом случае сравниваются дисперсии одной и той же оценки при разных размерах выборки.

же теоретического параметра, можно ли утверждать, что оценка с меньшей

дисперсией будет более эффективной?

УПРАЖНЕНИЕ О.20

того же теоретического параметра, можно ли утверждать, что оценка с

меньшей дисперсией будет более эффективной?



Если обе оценки несмещенные, то так утверждать можно, считая, что обе оценки рассматриваются на одной и той же выборке.

Если оценки (или хотя бы одна из них) смещенные, то необязательно.
Понятие эффективности используется для сравнения несмещенных оценок. Для сравнения смещенных и несмещенных оценок используется обобщение этого понятия на основе функции потерь. Та оценка считается более эффективной, для которой функция потреь имеет наименьшее математическое ожидание.

ДОМОЙ

и теоретической дисперсией sX. Имеется выборка из n наблюдений {X1,

..., Xn}. Является ли выборочное среднее



состоятельной оценкой теоретического среднего?

2

и теоретической дисперсией s 2X. Имеется выборка из n наблюдений

{X1, ..., Xn}. Является ли оценка Z






состоятельной оценкой теоретического среднего?