Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы общей алгебры
Содержание
- 1. Элементы общей алгебры
- 2. «Алгебра — не что иное, как записанная
- 3. Бинарная операция Бинарная операция — это отображение
- 4. Свойства бинарных операцийАссоциативностьКоммутативностьДистрибутивность слева и справаСуществование нейтрального элементаРазрешимость уравненийСуществование обратного элемента
- 5. ГруппоидГруппоид, обозначаемый символом (A, ) — множество
- 6. Полугруппа — множество, с определенной на нем
- 7. Квазигруппа (от латинского слова quasi — как будто, почти
- 8. Формальное определение группыГруппа (нем. Gruppe) — одно из основных
- 9. Алгебраические системыМножество M с заданными на нем
- 10. ИЗОМОРФИЗМ (от греческих слов – равный
- 11. ГОМОМОРФИЗМ – (от греческих слов –
- 12. ЭПИМОРФИЗМ – (от греческих слов –
- 13. Иерархия систем с двумя бинарными операциями Основные определения
- 14. Кольцо
- 15. Если
- 16. ТелоТело есть такая система (A, + ,
- 17. ПолеПоле может быть определено как множество, содержащее
- 18. Решетка, структураРешетка, структура, — частично упорядоченное множество,
- 19. Решетка как универсальная алгебраРешетка может быть также
- 20. Примеры решеток 1) множество всех подмножеств данного
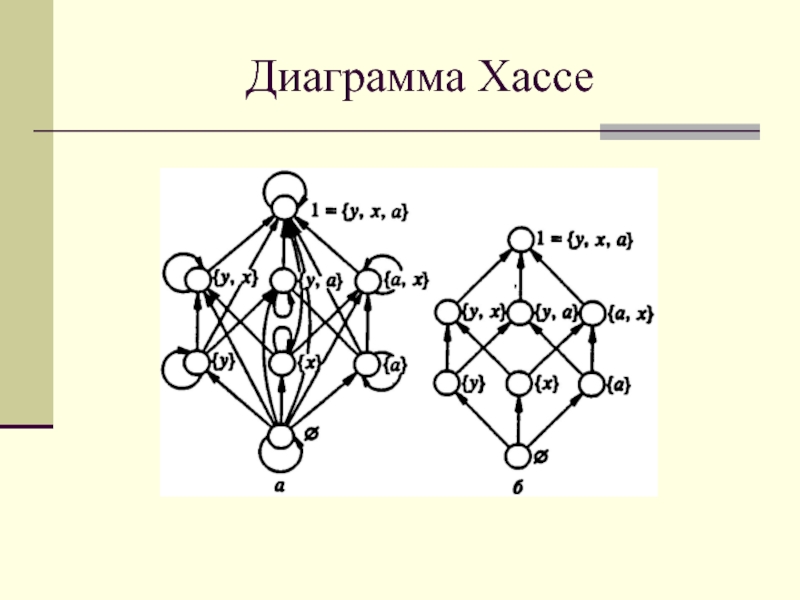
- 21. Диаграмма Хассе
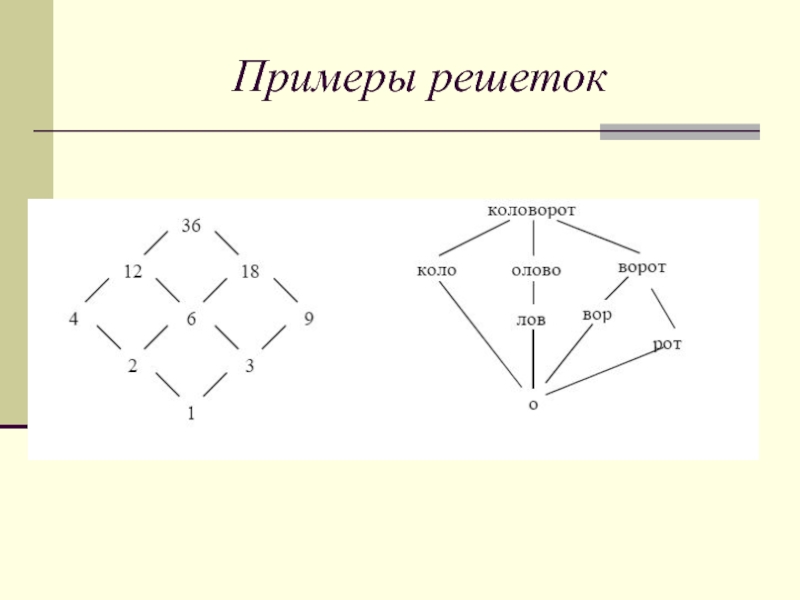
- 22. Примеры решеток
- 23. Скачать презентанцию
«Алгебра — не что иное, как записанная в символах геометрия, а геометрия — это просто алгебра, воплощенная в фигурах»Софи ЖерменАлгебра — наука об алгебраических операциях, выполняемых над элементами различных множеств
Слайды и текст этой презентации
Слайд 1Элементы общей алгебры
Алгебра учит вычислениям с любыми объектами, для
которых определены действия, удовлетворяющие основным алгебраическим аксиомам
Слайд 2«Алгебра — не что иное, как записанная в символах геометрия,
а геометрия — это просто алгебра, воплощенная в фигурах»
Софи Жермен
Алгебра
— наука об алгебраических операциях, выполняемых над элементами различных множествСлайд 3Бинарная операция
Бинарная операция — это отображение множества A
A в множество A, при этом образ пары (x, y) обозначим,
например, x y, где — символ операции. Здесь A — произвольное непустое множество и AA — множество всех упорядоченных пар (x, y) — таких, что x, y A. Непустое множество A называется основным множеством операции.Можно составить иерархию множеств с бинарной операцией (разумеется, вместо может быть вставлена любая — +, –, *, , , , , , и т.д. и т.п.).
Слайд 4Свойства бинарных операций
Ассоциативность
Коммутативность
Дистрибутивность слева и справа
Существование нейтрального элемента
Разрешимость уравнений
Существование обратного
элемента
Слайд 5Группоид
Группоид, обозначаемый символом (A, ) — множество A, на котором
задана некоторая бинарная операция, обозначаемая . Если множество группоида конечно,
то есть A = card (A) = n, то таблица Кэли операции группоида есть таблица n n, в которой элемент x y A находится в клетке пересечения строки x и столбца y. Конечный группоид можно считать заданным, если выписана его таблица Кэли.Слайд 6Полугруппа — множество, с определенной на нем бинарной операцией, удовлетворяющей
закону ассоциативности, т.е. группоид (A,), в котором для каждой тройки
элементов a , b и с выполняется условие a ( b с) = (a b) с.Моноид — это, по определению, полугруппа с единицей.
Слайд 7Квазигруппа (от латинского слова quasi — как будто, почти и слова группа) — группоид,
бинарная операция которого (например, ) такова, что каждое из уравнений
a x = b, y a = b имеет единственное решение для любых элементов a, b этого множества.Лупа, или квазигруппа с единицей, определение которой получается из аксиом группы отбрасыванием требования ассоциативности, особенно близка к группе.
Слайд 8Формальное определение группы
Группа (нем. Gruppe) — одно из основных понятий современной математики
— есть лупа, являющаяся в то же время полугруппой.
Пусть G — произвольное непустое множество, на котором задана бинарная алгебраическая операция , т.е. для любых двух элементов a и b из G определен некоторый элемент (обозначаемый, например, a b) также из G. Если при этом выполняются условия:
1) (a b) c = a (b c) для любых a, b и c из G;
2) в G существует такой элемент e (называемый единицей, иногда — нейтральным элементом), что a e = e a = a для любого a из G;
3) для любого a из G существует такой элемент a –1 (обратный к a элемент), что a a –1 = a –1 a = e,
то множество G с заданной на нем операцией назовем группой.
Абелева группа есть группа (A, ), в которой для любых двух элементов a , b A имеет место a b = b a .
Слайд 9Алгебраические системы
Множество M с заданными на нем операциями {1, 2,…,
m} называется алгеброй. Обозначение алгебры: A = (M; 1, 2,…,
m), где M — называется основным множеством (несущим множеством, носителем) алгебры, а = {1, 2,…, m} — сигнатурой алгебры A.Типом алгебры A называется вектор арностей операций сигнатуры.
Множество M с заданными на нем отношениями {R1, R2,…, Rn} называется моделью. Обозначение модели: M = (M; R1, R2,…, Rn), где M — несущее множество (универсум) модели, а = { R1, R2,…, Rn} — сигнатурой модели M.
Множество M с заданными на нем операциями {1, 2,…, m} и отношениями {R1, R2,…, Rn} называется алгебраической системой или алгебраической структурой. Обозначение алгебраической структуры: M = (M; 1, 2,…, m; R1, R2,…, Rn).
Слайд 10ИЗОМОРФИЗМ (от греческих слов – равный и –
образ, вид, форма) – это одно из основных понятий современной
математики, которое исторически возникло сначала в пределах алгебры в применении к таким алгебраическим системам, как группы, кольца, поля и др., но оказавшееся принципиально существенным для общего понимания строения и структуры самых разных систем.Пусть даны две системы объектов S и S/ , причем в первой системе S определены отношения Fk (x1, x2, ...), k = 1, 2, ..., n, а во второй системе S/ – определены отношения F/k (x/1, x/2, ...), k = 1, 2, ..., n. Системы S и S/ с указанными на них здесь отношениями называются изоморфными, если между ними существует такое взаимно однозначное соответствие x/=(x), x = (x/), где x – произвольный элемент системы S, а x/ – произвольный элемент системы S/, что из наличия Fk (x1, x2, ...) вытекает F/k (x/1, x/2, ...), и наоборот. Отображение называется в этом случае изоморфным отображением или изоморфизмом системы S на систему S/, а обратное ему отображение – изоморфизмом системы S/, на систему S. Факт изоморфности систем S и S/ обозначается следующим образом: SS /.
Слайд 11ГОМОМОРФИЗМ – (от греческих слов – равный, одинаковый и
) – отображение множества элементов одной алгебраической системы в (в
том числе на) другую, сохраняющее все значимые отношения (в частности, все операции).АВТОМОРФИЗМ (от греческих слов – сам и ) – изоморфизм некоторой системы объектов на себя.
ЭНДОМОРФИЗМ – (от греческих слов – внутри и ) – гомоморфизм алгебраической системы в (в том числе и на) себя.
Слайд 12ЭПИМОРФИЗМ – (от греческих слов – на, над, при,
после и ) или, что то же самое, сюръективное отображение
(СЮРЪЕКЦИЯ) множества A на множество B – отображение f такое, что образ A есть все B, т.е. f(A)=B.МОНОМОРФИЗМ – (от греческих слов – один и ) или, что то же самое, инъективное отображение (ИНЪЕКЦИЯ) множества A в множество B – отображение, при котором различные элементы из A имеют различные образы в B. Инъективное отображение называют также взаимно однозначным отображением множества A в множество B или вложением.
БИМОРФИЗМ – (от латинского bi – двойной, двоякий и ) или, что то же самое, биективное отображение (БИЕКЦИЯ) –мономорфизм и эпиморфизм одновременно.
Слайд 14Кольцо
Кольцом называется непустое
множество R, для элементов которого определены две бинарные операции —
сложение и умножение (обозначаемые и соответственно; знак обычно опускается), причем предполагаются выполненными следующие аксиомы колец (a, b, c R):Коммутативность сложения: a b = b a.
Ассоциативость сложения:
a (b c) = (a b) c.
Обратимость сложения (возможность вычитания): уравнение a x = b имеет решение x = b a R.
Дистрибутивность умножения относительно сложения:
a (b c) = a b a c и (b c) a = b a c a.
Слайд 15Если
, то кольцо называют ассоциативным;
если
, альтернативным; если ab = ba и , йордановым;
если a2 = a, a(bc) + b(ca) +c(ab) = 0, то оно называется кольцом Ли;
если ab = ba , то кольцо называется коммутативным.
Примеры колец:
множество всех целых чисел;
множество всех четных чисел и вообще целых чисел, кратных данному числу m;
множество всех рациональных чисел;
множество всех многочленов от одного или нескольких переменных с рациональными, действительными или комплексными коэффициентами;
множество всех функций, непрерывных на данном отрезке числовой прямой
Слайд 16Тело
Тело есть такая система (A, + , ), что система
(A, +) является абелевой группой, а система (A, ), где
A получается из A удалением нулевого элемента (т.е. нейтрального элемента абелевой группы), является группой и операция дистрибутивна относительно операции + .Теорема. Кольцо является телом тогда и только тогда, когда оно содержит не менее двух элементов и оба уравнения ax = b и xa = b, разрешимы для любых элементов a, b A, где a 0.
Тело служит обобщением системы (Q, + , ) рациональных чисел, однако требование коммутативности умножения опускается.
Теорема Веддербёрна. Всякое конечное тело коммутативно.
Слайд 17Поле
Поле может быть определено как множество, содержащее не менее двух
элементов, на котором заданы две бинарные алгебраические операции — сложение
и умножение, обе ассоциативные и коммутативные, связанные между собой законом дистрибутивности, т.е. для любых a, b, c из поля справедливо:a b b a , ab ba ,
(a b) c a (b c), (ab) c a (bc),
(a b) c ac bc .
Кроме того, в поле требуется существование нулевого элемента 0 (нуля), для которого 0 a a , и для каждого элемента a противоположного элемента –a, то есть такого элемента, что a (–a ) 0, а также существование единичного элемента e (единицы), для которого ae a, и для каждого ненулевого элемента a существование обратного элемента a–1, т.е. такого элемента, что aa–1 e. Отсюда следует, что в поле выполнимы операция вычитания, а также операция деления на ненулевой элемент. Таким образом, все элементы поля образуют абелеву группу по сложению (аддитивная группа поля), а все ненулевые элементы — абелеву группу по умножению (мультипликативная группа поля).
Слайд 18Решетка, структура
Решетка, структура, — частично упорядоченное множество, в котором каждое
двухэлементное подмножество имеет как точную верхнюю (sup), так и точную
нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.Слайд 19Решетка как универсальная алгебра
Решетка может быть также определена как универсальная
алгебра с двумя бинарными операциями (они обозначаются и
или и , а также и ), удовлетворяющая следующим тождествам(1) a a = a, (1) a a = a {идемпотентность},
(2) a b = b a, (2) a b = b a {коммутативность},
(3) (a b) c = a (b c), (3) (a b) c = a (b c) {ассоциативность},
(4) a (a b) = a, (4) a a b = a {поглощение}.
Связь между этими двумя определениями устанавливается при помощи формул:
a b = sup {a, b}, a b = inf {a, b},
и обратно. При этом для любых элементов a и b эквивалентны следующие утверждения: (а) a b ; (б) a b = a; (в) a b = b. Понятия изоморфизма решеток как универсальных алгебр и как частично упорядоченных множеств совпадают. Однако произвольное изотонное отображение решетки R в решетку R не обязано быть гомоморфизмом этих решеток как универсальных алгебр.
Слайд 20Примеры решеток
1) множество всех подмножеств данного множества, упорядоченное по
включению;
2) всякое линейно упорядоченное множество; причем если a b, то
sup{a, b} = b, а inf {a, b} = a;3) множество всех надпространств векторного пространства, упорядоченных по включению, где inf — пересечение, а sup — сумма соответствующих надпространств;
4) множество всех неотрицательных целых чисел, упорядоченных по делимости: a b , если b = ac для некоторого c. Здесь sup — наименьшее общее кратное, а inf — наибольший общий делитель данных чисел;