Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЭЛЕМЕНТЫ теории множеств
Содержание
- 1. ЭЛЕМЕНТЫ теории множеств
- 2. ЭпиграфВ любых делах при максимуме сложностейПодход проблеме
- 3. История появленияТеория множеств возникла в результате реализации
- 4. История появленияПервый набросок теории множеств принадлежит Бернарду
- 5. История появленияВ XVIII веке Леонард Эйлер использовал
- 6. История появленияДжон Венн (1834–1923)В XIX веке сходное
- 7. ЗаданиеПриведите житейские названия следующих множеств:1) множество марок,
- 8. Понятие множества«Множество есть многое, мыслимое как единое
- 9. Символы и обозначенияА, В, С, D, …
- 10. Мощность множестваМощностью конечного множества называется количество его элементов. Обозначение |A|.
- 11. 1) перечисление всех его элементов. A={студент А.,
- 12. 10–1Способы задания множествЗадайте множество всех целых чисел,
- 13. ЗаданиеИзмените способ задания множества: а) А –
- 14. Задание
- 15. Отношения между множествамиМножества A и B называются
- 16. Отношения между множествамиМножество B называется подмножеством множества
- 17. Задание
- 18. ЗаданиеИзобразите с помощью диаграмм Эйлера-Венна отношения следующих
- 19. ЗаданиеУстановите соответствие между множествами и верными для них высказываниями.
- 20. Операции над множествамиОбъединением множеств А и В
- 21. Операции над множествамиПересечением двух множеств А и
- 22. Операции над множествамиРазностью множеств А и В
- 23. Операции над множествамиДополнением к множеству A называется разность между универсальным множеством и множеством A.
- 24. Задание
- 25. Задание
- 26. Задание
- 27. ЗаданиеВ школе 1400 учеников. Из них 1250
- 28. ЗаданиеКаждая из 30 невест, зарегистрированных
- 29. РешениеВ – множество воспитанных невест К –
- 30. Формула включений-исключений…–––+1.2.3.
- 31. Скачать презентанцию
ЭпиграфВ любых делах при максимуме сложностейПодход проблеме все-таки один:Желанье – это множество возможностей,А нежеланье – множество причин.Эдуард Асадов
Слайды и текст этой презентации
Слайд 2Эпиграф
В любых делах при максимуме сложностей
Подход проблеме все-таки один:
Желанье –
это множество возможностей,
Слайд 3История появления
Теория множеств возникла в результате реализации программы стандартизации математики,
разработанной немецким математиком Георгом Кантором (1845–1918).
Множество есть «объединение в одно
целое объектов, хорошо различимых нашей интуицией или мыслью» Георг Кантор (1845–1918)
Слайд 4История появления
Первый набросок теории множеств принадлежит Бернарду Больцано («Парадоксы бесконечного»,
1850). В этой работе рассматриваются произвольные (числовые) множества, и для
их сравнения определено понятие взаимно-однозначного соответствия.Бернард Больцано (1781–1848)
Слайд 5История появления
В XVIII веке Леонард Эйлер использовал круги в качестве
наглядно-графическое изображение множества
Леонард Эйлер (1707–1783)
“…Эти круглые фигуры, или, вернее, пространства
способны облегчить ход наших рассуждений, а также позволяют нам раскрыть все тайны, которыми похваляется логика. С помощью этих символов всё сразу бросается в глаза…”
Слайд 6История появления
Джон Венн (1834–1923)
В XIX веке сходное изображение множеств использовал
английский логик Джон Венн.
Он изображал множества прямоугольниками, и использовал
эти изображения для доказательства утверждений о множествах 
Слайд 7Задание
Приведите житейские названия следующих множеств:
1) множество марок, принадлежащих одному человеку;
2) множество пчел, летящих вместе; 3) множество цветных карандашей в
коробке; 4) множество военных, подчиняющихся одному командиру; 5) множество футболистов, собравшихся вместе для игры; 6) множество цветов, в руке первоклассницы.Что во всех этих случаях вы понимаете под множеством?
Слайд 8Понятие множества
«Множество есть многое, мыслимое как единое целое»
Множество - совокупность
объектов, определяемых некоторым свойством, присущим каждому из них.
Каждый объект, входящий
в множество, называется его элементом, а свойство их объединяющее – характеристическим свойством множества.
Слайд 9Символы и обозначения
А, В, С, D, … – множества
a, b,
с, d, … – элементы множества
При записи множества перечислением его
элементов используют символ «{ }». – символ принадлежности элемента множеству
– пустое множество
Слайд 10Мощность множества
Мощностью конечного множества называется количество его элементов.
Обозначение |A|.
Слайд 111) перечисление всех его элементов.
A={студент А., рабочий Л., школьник
М.}
2) указание общего свойства элементов
В - множество четных натуральных чисел.
В
= {b| b = 2k, k — любое натуральное число}.3) Символьное обозначение
N – множество натуральных чисел
Z – множество целых чисел
Q – множество рациональных чисел
R – множество действительных чисел
I – множество иррациональных чисел
4) Указание концов числового промежутка
[2; 8], (0; 6,5)
Способы задания множеств
Слайд 121
0
–1
Способы задания множеств
Задайте множество всех целых чисел, удовлетворяющих неравенству
:
a) перечислением элементов;
б) заданием характеристического свойства;
в) изображением на координатной прямой.
{–1; 0; 1}
Слайд 15Отношения между множествами
Множества A и B называются равными, если они
состоят из одних и тех же элементов. Обозначение: A=B.
{a, b, c, d} = {c, b, a, d}
Слайд 16Отношения между множествами
Множество B называется подмножеством множества A, если каждый
элемент множества B является элементом множества A. Обозначение: B ⊂
A.В
А
Множество, по отношению к которому в данный момент все остальные множества являются подмножествами, называется универсальным множеством. Обозначение: U.
Слайд 18Задание
Изобразите с помощью диаграмм Эйлера-Венна отношения следующих множеств:
1) R,
Z, N, I и Q;
2) четырехугольников, параллелограммов, прямоугольников, ромбов
и квадратов. N
Z
Q
R
четырехугольники
парал.
П
Р
К
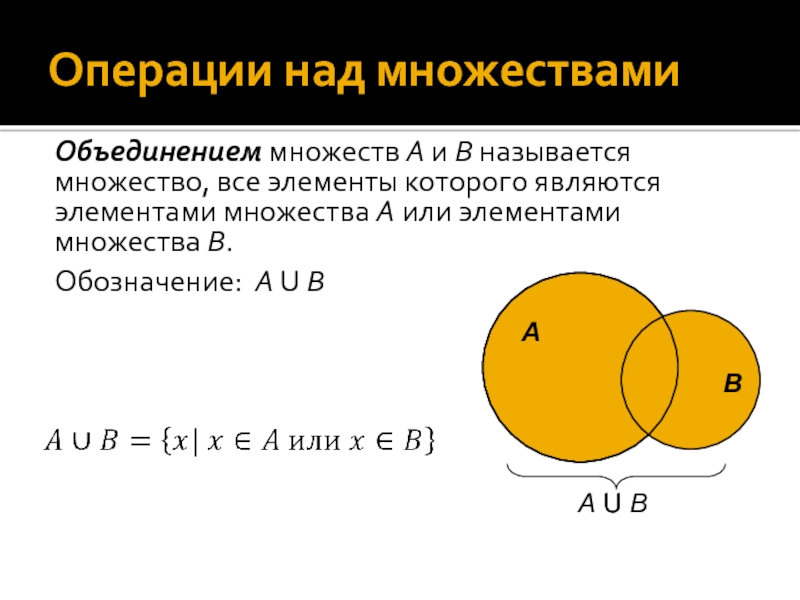
Слайд 20Операции над множествами
Объединением множеств А и В называется множество, все
элементы которого являются элементами множества А или элементами множества В.
Обозначение: А U B
А
В
А U В
Слайд 21Операции над множествами
Пересечением двух множеств А и В называется множество,
состоящее из тех и только тех элементов, которые принадлежат множеству
А и множеству В одновременно.Обозначение
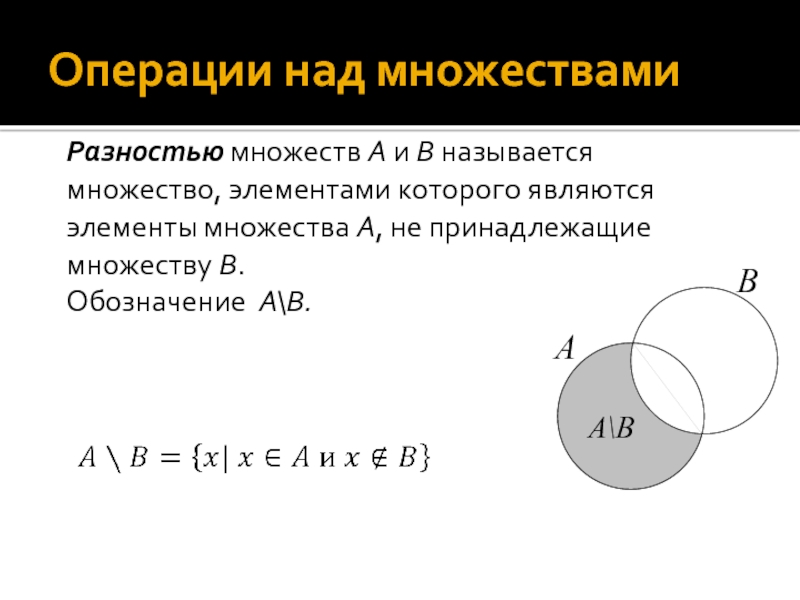
Слайд 22Операции над множествами
Разностью множеств А и В называется множество, элементами
которого являются элементы множества А, не принадлежащие множеству В.
Обозначение А\В.
А\B
А
В
Слайд 23Операции над множествами
Дополнением к множеству A называется разность между универсальным
множеством и множеством A.
Слайд 27Задание
В школе 1400 учеников. Из них 1250 умеют кататься на
лыжах, 952 – на коньках. Ни на лыжах, ни на
коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на коньках и на лыжах?
Слайд 28Задание
Каждая из 30 невест, зарегистрированных
в клубе знакомств,
красива, воспитана или умна. Воспитанных невест – 21, красивых –
18,умных – 15. Красивых и воспитанных – 11,
умных и воспитанных – 9, умных и красивых – 7. Сколько невест обладает всеми тремя качествами?
В – множество воспитанных невест
К – множество красивых невест
У – множество умных невест
Слайд 29Решение
В – множество воспитанных невест
К – множество красивых невест
У – множество умных невест
У
В
К
15
21
18
|B|=21, |K|=18, |У|=15
х
21 + 18
+ 15 – 9 – 11 – 7 + х = 3011
9
7
|В ∪ К ∪ У| = 30
х + (9 – х) + (7 – х) + (11 – х) +
+ (15 – 7 – (9 – х)) + (18 – 11 – (7 – х)) + (21– 9 – (11 – х))
= 30
х = 3
