Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Содержание
- 1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2. Теория вероятностей?ЕГЭ
- 3. Теория вероятностей – раздел математики, изучающий закономерности
- 4. История возникновения теории вероятностей Возникновение
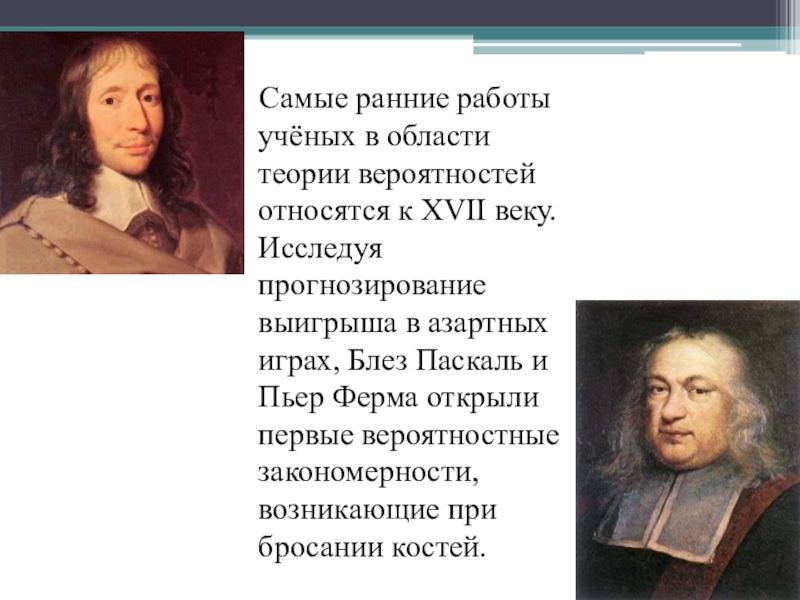
- 5. Самые ранние работы учёных в
- 6. Под влиянием поднятых и рассматриваемых
- 7. Его работа, в которой вводятся
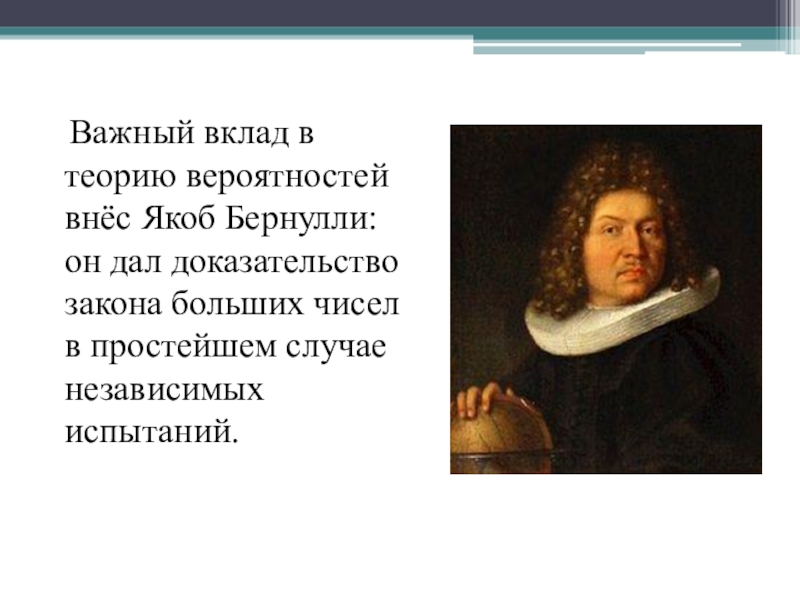
- 8. Важный вклад в теорию вероятностей
- 9. В первой половине XIX века
- 10. Во второй половине XIX века основной
- 11. Современный вид теория вероятностей получила
- 12. Вероятность случайного события Вероятностью события А
- 13. ЗАДАЧА НА ОПРЕДЕЛЕНИЕ КЛАССИЧЕСКОЙ ВЕРОЯТНОСТИ В сборнике
- 14. Решите самостоятельно: В сборнике билетов по
- 15. Основные виды задач
- 16. 1 вид. В соревнованиях по толканию ядра
- 17. В соревновании по толканию ядра участвуют 4
- 18. 2 вид. Фабрика выпускает сумки. В среднем
- 19. Фабрика выпускает сумки. В среднем на 80
- 20. 3 вид. В случайном эксперименте бросают две
- 21. В случайном эксперименте бросают три игральные кости.
- 22. 4 вид. В случайном эксперименте симметричную монету
- 23. В случайном эксперименте симметричную монету бросают трижды.
- 24. 5 вид. В сборнике билетов по биологии
- 25. В сборнике билетов по математике всего 20
- 26. 6 вид. Научная конференция проводится в 5
- 27. Конкурс исполнителей проводится в 3 дня. Всего
- 28. 7 вид. В среднем из 2000 садовых
- 29. В среднем из 1000 садовых насосов, поступивших
- 30. 8 вид. Перед началом первого тура чемпионата
- 31. Перед началом первого тура чемпионата по фехтованию
- 32. Найди ошибкиСлучайные события:Завтра пойдет снегПри подбрасывании симметричной
- 33. Теория вероятностей?вид задачи
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Теория вероятностей – раздел математики, изучающий закономерности случайный явлений: случайные
события, случайные величины, их свойства и операции над ними
Слайд 4История возникновения теории вероятностей
Возникновение теории вероятностей как науки
относят к средним векам и первым попыткам математического анализа азартных
игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмперическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях.Слайд 5 Самые ранние работы учёных в области теории вероятностей
относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх,
Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей.Слайд 6 Под влиянием поднятых и рассматриваемых ими вопросов решением
тех же задач занимался и Христиан Гюйгенс. При этом с
перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно.Слайд 7 Его работа, в которой вводятся основные понятия теории
вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных
случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год).Слайд 8 Важный вклад в теорию вероятностей внёс Якоб Бернулли:
он дал доказательство закона больших чисел в простейшем случае независимых
испытаний.Слайд 9 В первой половине XIX века теория вероятностей начинает
применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые
предельные теоремы.Слайд 10 Во второй половине XIX века основной вклад внесли русские
учёные П.Л.Чебышев, А.А.Марков и А.М.Ляпунов. В это время были доказаны
закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.Слайд 11 Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной
Андрей Николаевич Колмогоров. В результате теория вероятностей приобрела строгий математический
вид и окончательно стала восприниматься как один из разделов математики.Слайд 12Вероятность случайного события
Вероятностью события А называется отношение числа m благоприятных
для этого события исходов к n числу всех равновозможных исходов
Вероятность
выражают в процентахВероятность события обозначается большой латинской буквой Р (от французского слова probabilite, что означает – возможность, вероятность)
Слайд 13ЗАДАЧА НА ОПРЕДЕЛЕНИЕ КЛАССИЧЕСКОЙ ВЕРОЯТНОСТИ В сборнике билетов по физике всего
50 билетов, в 12 из них встречается вопрос по конденсаторам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по конденсаторамРешение:
m=50-12=38 –билетов без конденсаторов
n=50 –всего билетов
Р(А)= =0,76 Ответ: 0,76
Слайд 14Решите самостоятельно: В сборнике билетов по химии всего 35 билетов, в
7 из них встречается вопрос по кислотам. Найдите вероятность того,
что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.Ответ: 0,8
Слайд 161 вид. В соревнованиях по толканию ядра участвуют 9 спортсменов
из Дании, 3 спортсмена из Швеции, 8 спортсменов из Норвегии
и 5 — из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из ФинляндииРешение
Всего участвует n = 9+3+8+5=25 спортсменов.
А т.к. финнов m = 5 человек, то вероятность того, что на последнем месте будет спортсмен из Финляндии
P = = 0,2
Слайд 17В соревновании по толканию ядра участвуют 4 спортсмена из Македонии,
9 спортсменов из Сербии, 7 спортсменов из Хорватии и 5
– из Словении. Порядок в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Македонииm = 4
n = 25
P = = 0,16
Слайд 182 вид. Фабрика выпускает сумки. В среднем на 180 сумок
приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что
купленная сумка окажется качественной. Результат округлите до сотых.Решение
m = 180-8 = 172 сумки качественные,
n= 180 всего сумок
P = = 0,955...≈ 0,96
Слайд 19Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится
8 сумок со скрытыми дефектами. Найдите вероятность того, что купленная
сумка окажется качественной.m = 80
n = 80+8=88
P = = 0,91
Слайд 203 вид. В случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 8 очков. Результат округлите
до сотых.Решение Игральные кости - это кубики с 6 гранями. На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому варианту выпадения очков соответствует 6 вариантов выпадения очков на втором кубике. Т.е. n = 6×6 = 36. Варианты (исходы эксперимента) будут такие:
1;1 1;2 1;3 1;4 1;5 1;6
2;1 2;2 2;3 2;4 2;5 2;6 и т.д. ..............................
6;1 6;2 6;3 6;4 6;5 6;6
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8: 2;6 3;5; 4;4 5;3 6;2 Всего m = 5 вариантов. Найдем вероятность.
P = = 0,138 ≈ 0,14
Слайд 21В случайном эксперименте бросают три игральные кости. Найдите вероятность того,
что в сумме выпадет 4 очка.
m = 3
это
1,1,21,2,1
2,1,1
n = 6 × 6× 6 = 216
P =
Слайд 224 вид. В случайном эксперименте симметричную монету бросают трижды. Найдите
вероятность того, что орел выпадет ровно два раза.
Решение
Всего вариантов n
= 2×2×2=8. Благоприятных m = 3 варианта: о; о; р
о; р; о р; о; о
Вероятность равна
P = = 0,375
Слайд 23В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того,
что орел не выпадет ни разу.
m = 1
это р, р,
рn = 2×2×2 = 8
P = = 0,125
Слайд 245 вид. В сборнике билетов по биологии всего 35 билетов,
в 14 из них встречается вопрос по зоологии. Найдите вероятность
того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по зоологии.Решение
m = 35-14=21- билет без зоологии
n = 35 – всего билетов
Вероятность равна
P = =0,6
Слайд 25В сборнике билетов по математике всего 20 билетов, в 13
из них встречается вопрос по производной. Найдите вероятность того, что
в случайно выбранном на экзамене билете школьнику не достанется вопроса по производнойm = 20 – 13 = 7
n = 20
P = = 0,35
Слайд 266 вид. Научная конференция проводится в 5 дней. Всего запланировано
80 докладов — первые три дня по 12 докладов, остальные распределены поровну между
четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?Решение
1 день – 12 докладов, 2 день – 12 докладов, 3 день – 12 докладов, 4 день – 22 доклада, т.к. (80- 3×12):2=22
5 день – m = 22 доклада. n = 80 – всего выступлений. Вероятность выступления профессора М:
P = = 0,275
Слайд 27Конкурс исполнителей проводится в 3 дня. Всего заявлено 75 выступлений
– по одному от каждой страны. В первый день 33
выступления, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьевкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?1 день – 33 выступления
2, 3 день – по (75-33):2=21 выступление
m = 21 n = 75
P = = 0,28
Слайд 287 вид. В среднем из 2000 садовых насосов, поступивших в
продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный
для контроля насос не подтекает.Решение
m = 2000-12=1988 - насосов не подтекает
n = 2000 – всего насосов
Вероятность, что случайно выбранный насос не подтекает:
P = =0,994
Слайд 29В среднем из 1000 садовых насосов, поступивших в продажу, 4
подтекают. Найдите вероятность того, что один случайно выбранный для контроля
насос не подтекаетm = 1000 – 4 = 996
n = 1000
P = = 0,996
Слайд 308 вид. Перед началом первого тура чемпионата по бадминтону участников
разбивают на игровые пары случайным образом с помощью жребия. Всего
в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?Решение
Так как Руслан Орлов сам с собой играть не может, то вероятность его игры с каким-нибудь спортсменом из России будет (m = 9, n = 25):
P = = 0,36
Слайд 31Перед началом первого тура чемпионата по фехтованию участников разбивают на
игровые пары случайным образом с помощью жребия. Всего в чемпионате
участвует 36 спортсменов, среди которых 8 участников из России, в том числе Василий Петров. Найти вероятность того, что в первом туре Василий Петров будет играть с каким-либо спортсменом из России?m = 7
n = 35
P = = 0,2
Слайд 32Найди ошибки
Случайные события:
Завтра пойдет снег
При подбрасывании симметричной монеты выпадет орел
Появление
более 12 очков при одновременном бросании двух игральных костей
2. Вероятность
купить исправную лампочку из 1000, если 3 бракованных, равна (1000 + 3) / 10003. При бросании симметричной монеты трижды существует = 6 вариантов выпадения очков
4. Если симметричную монету бросить четыре раза, то вероятность того, что орел не выпадет ни разу равна нулю
5. Если из 2000 садовых насосов подтекает 12, то вероятность того, что один случайно выбранный насос не подтекает равна 12 /2000
































![ДИФФЕРЕНЦИАЦИЯ ЗВУКОВ [Л] - [Р]
В СЛОГАХ, СЛОВАХ](/img/thumbs/8747bbe13d20063553fa1f12a186718b-800x.jpg)