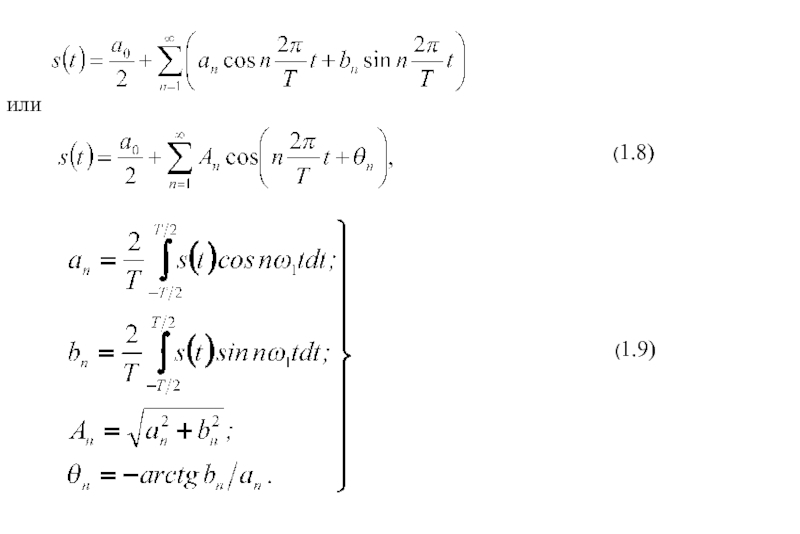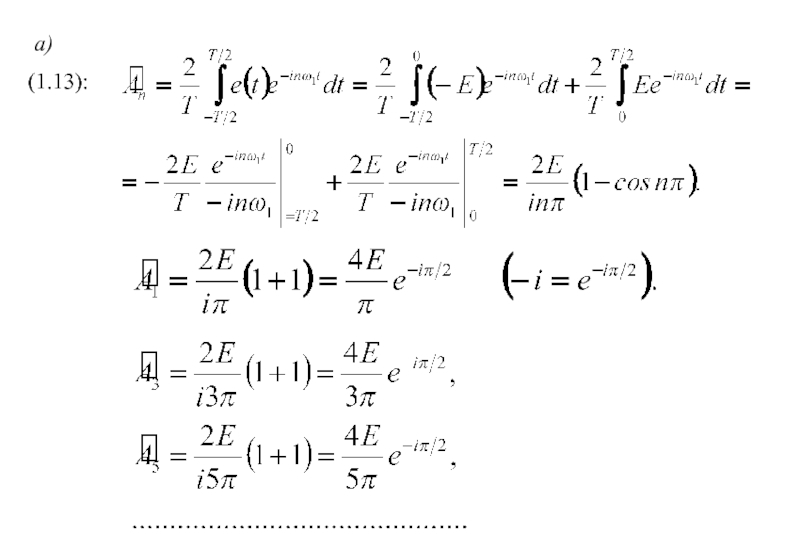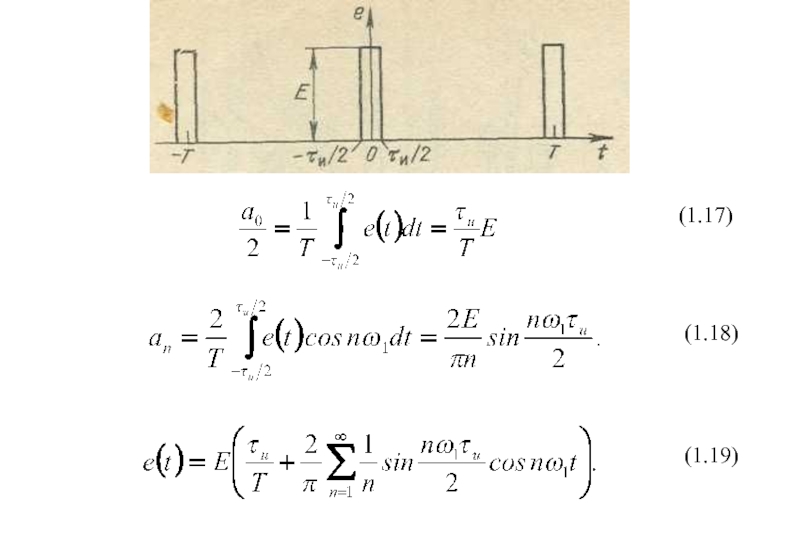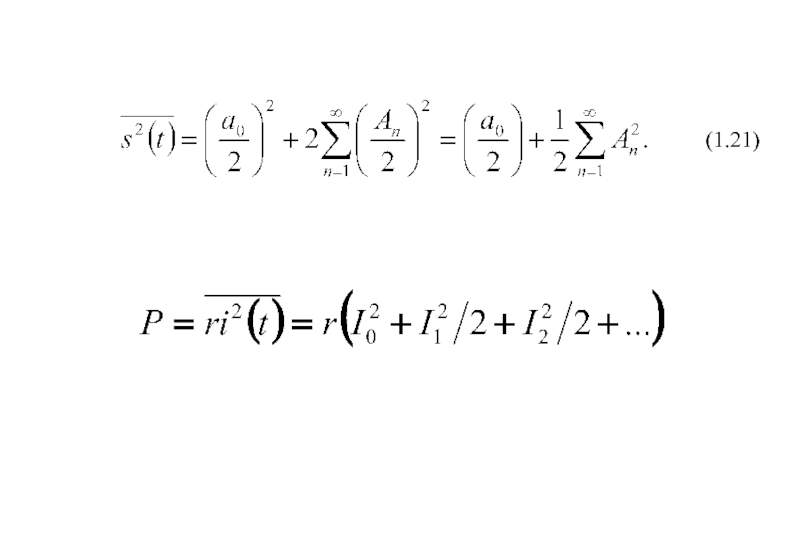Энергетические характеристики и разложение в ряд

Содержание

1. Энергетические характеристики и разложение в ряд
2. Разложение колебаний по системам ортогональных функций удовлетворяет
3. Заданное колебание можно разложить по системе
4. Одним из возможных критериев величины этой разности
5. Для определения коэффициентов cn, обеспечивающих минимум Δ,
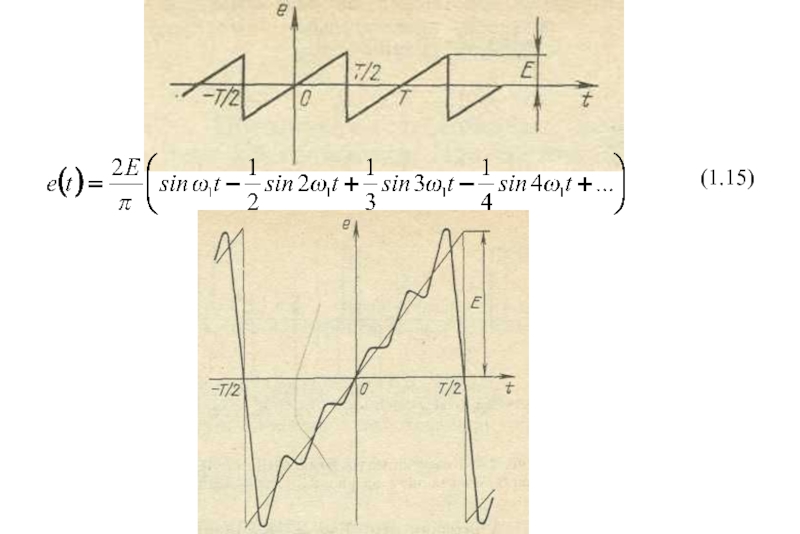
6. Разложение периодических колебаний в ряд Фурьепо системе тригонометрических функций(1.7)
7. или(1.8)(1.9)
8. Ряд Фурье в комплексной форме Положим α
9. После этого ряд (1.8) можно записать в
10. Формулы (1.12) и (1.13) можно называть парой
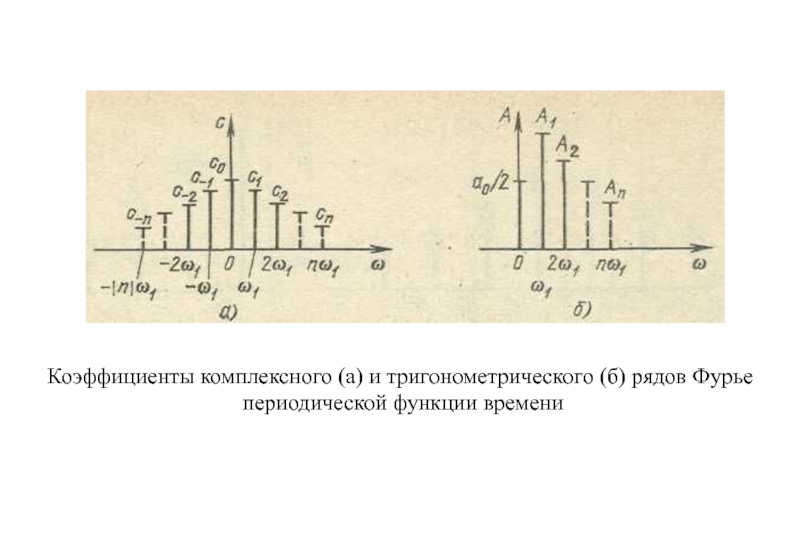
11. Коэффициенты комплексного (а) и тригонометрического (б) рядов Фурье периодической функции времени
12. Слайд 12
13. (1.13):а)
14. Рис. 3. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье(1.13)
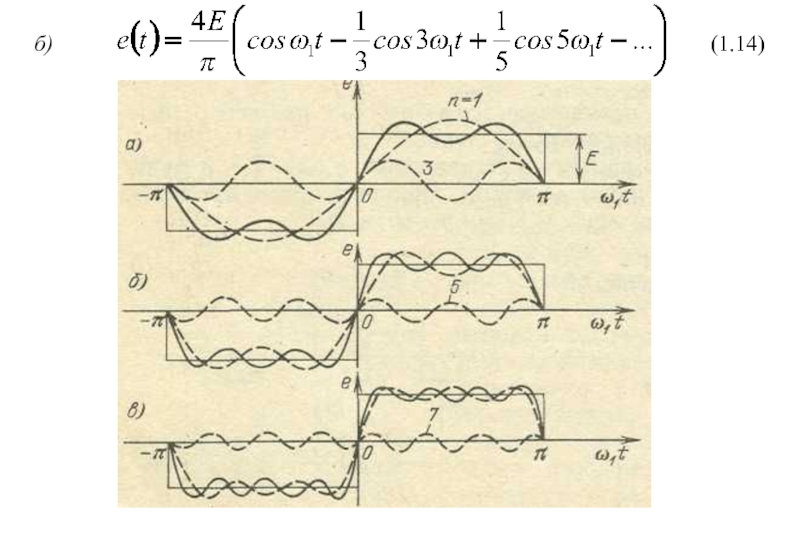
15. б)(1.14)
16. (1.15)
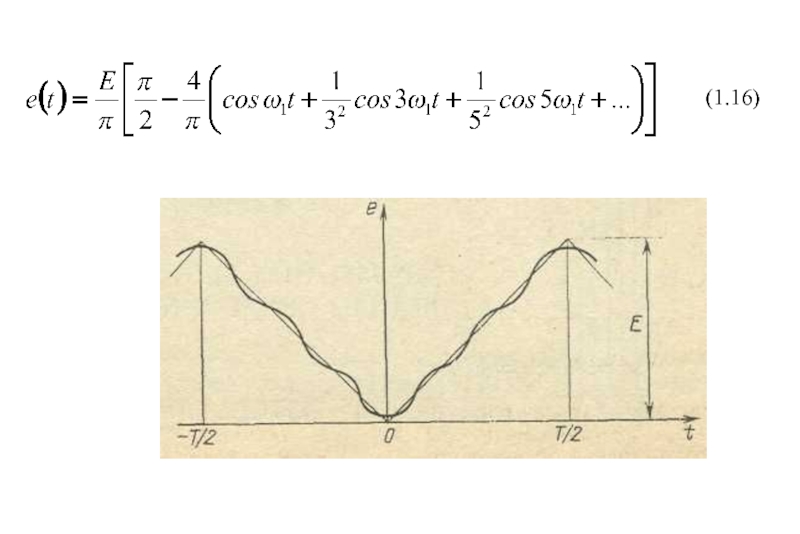
17. (1.16)
18. (1.19)(1.18)(1.17)
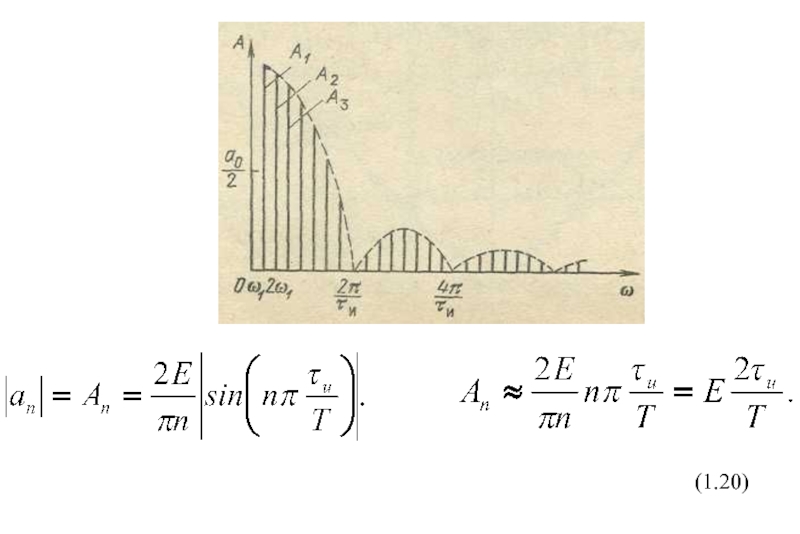
19. (1.20)
20. (1.21)
21. Скачать презентанцию

Разложение колебаний по системам ортогональных функций удовлетворяет на некотором отрезке времени (t1, t2) условиям Если совокупность функцийто ее называют системой ортогональных на отрезке (t1, t2) функций. При этом предполагается, что никакая

Главная
Разное
Энергетические характеристики и разложение в ряд

Слайды и текст этой презентации

Слайд 1Энергетические характеристики
Мгновенная мощность определяется как квадрат мгновенного значения s(t):

Энергия сигнала

на интервале t2, t1 определяется как интеграл от мгновенной мощности:

Отношение

имеет

смысл средней на интервале t2, t1 мощности сигнала.

Энергетические характеристикиМгновенная мощность определяется как квадрат мгновенного значения s(t): Энергия сигнала на интервале t2, t1 определяется как интеграл

Слайд 2Разложение колебаний по системам ортогональных функций

удовлетворяет на некотором отрезке времени

(t1, t2) условиям

Если совокупность функций

то ее называют системой ортогональных

на отрезке (t1, t2) функций. При этом предполагается, что никакая из функций системы (1.1) не равна тождественно нулю, т.е.

(1.1)

(1.2)

Разложение колебаний по системам ортогональных функций удовлетворяет на некотором отрезке времени (t1, t2) условиям Если совокупность функцийто

Слайд 3

Заданное колебание можно разложить по системе ортогональных функций, если

можно записать
и
.
(1.5)

Величина
называется нормой функции
.
Функция
,

для которой

называется нормированной, а соответствующая система ортогональных нормированных функций называется ортонормированной (ортонормальной)

и при конечном числе членов ряда разница между

будет достаточна мала.

(1.4)

(1.3)

Заданное колебание можно разложить по системе ортогональных функций, если можно записать и . (1.5)Величина называется нормой

Слайд 4Одним из возможных критериев величины этой разности является интеграл от

квадрата разности колебания и его разложения:
Если для непрерывной функции s(t)

можно выбрать xn так, что путем
увеличения количества членов в ряде Δ можно сделать сколь угодно
малым, то совокупность ортогональных (ортонормальных) функций
(1.1) называют полной. Ряд (1.4) называют в этом случае
сходящимся в среднем.

(1.5)

Одним из возможных критериев величины этой разности является интеграл от квадрата разности колебания и его разложения:Если для

Слайд 5Для определения коэффициентов cn, обеспечивающих минимум Δ, умножим обе части

(1.4) на и произведем интегрирование:
В силу свойств ортогональности в правой

части уравнения все слагаемые при m≠n обращаются в ноль, остается лишь член, соответствующий n=m. В результате получаем формулу для любого коэффициента cn

(1.6)

Для определения коэффициентов cn, обеспечивающих минимум Δ, умножим обе части (1.4) на и произведем интегрирование:В силу свойств

Слайд 6Разложение периодических колебаний в ряд Фурье
по системе тригонометрических функций

(1.7)

Слайд 7

или

(1.8)
(1.9)

Слайд 8Ряд Фурье в комплексной форме

Положим α = nω1t +

θn и обозначим

Эту величину назовем комплексной амплитудой n-й гармоники.
Она

содержит данные и об амплитуде и о начальной фазе n-й гармоники.

(1.11)

(1.10)

Ряд Фурье в комплексной форме Положим α = nω1t + θn и обозначим Эту величину назовем комплексной

Слайд 9После этого ряд (1.8) можно записать в таком виде:
где

- величина,

комплексно-сопряжённая

Комплексную амплитуду можно вычислить непосредственно

по заданному
s(t), минуя вычисления an и bn и применение выражений (1.10). Действительно,

Подставляя сюда (1.9) и объединяя интегралы, получаем

(1.12)

(1.13)

После этого ряд (1.8) можно записать в таком виде:где- величина, комплексно-сопряжённая Комплексную амплитуду

Слайд 10Формулы (1.12) и (1.13) можно называть парой преобразований Фурье.
Вторая из

них позволяет найти спектр, т. е. совокупность гармонических
составляющих, образующих в

сумме s(t); первая – вычислить s(t), если
заданы гармонические составляющие (гармоники)

Формулу (1.12) можно представить в другом виде

Две характеристики – амплитудная и фазовая, т. е. модули и аргументы
комплексных коэффициентов ряда Фурье, полностью определяют структуру
частотного спектра периодического колебания.

Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных линий, соответствующих дискретным частотам 0, ω1, 2ω1, 3ω1 и т. д.

(1.12а)

Формулы (1.12) и (1.13) можно называть парой преобразований Фурье.Вторая из них позволяет найти спектр, т. е. совокупность

Слайд 11Коэффициенты комплексного (а) и тригонометрического (б) рядов Фурье
периодической функции

времени

Слайд 12

Слайд 13

(1.13):

а)

Слайд 14
Рис. 3. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье
(1.13)

Слайд 15
б)
(1.14)

Слайд 16
(1.15)

Слайд 17
(1.16)

Слайд 18

(1.19)
(1.18)
(1.17)

Слайд 19

(1.20)

Слайд 20

(1.21)

Скачать презентацию

Разделы презентаций

Энергетические характеристики и разложение в ряд

Содержание

Слайды и текст этой презентации

Слайд 1Энергетические характеристики
Мгновенная мощность определяется как квадрат мгновенного значения s(t):

Энергия сигнала

на интервале t2, t1 определяется как интеграл от мгновенной мощности:

Отношение

имеет

Слайд 2Разложение колебаний по системам ортогональных функций

удовлетворяет на некотором отрезке времени

(t1, t2) условиям

Если совокупность функций

то ее называют системой ортогональных

Слайд 3

Заданное колебание можно разложить по системе ортогональных функций, если

можно записать
и
.
(1.5)

Величина
называется нормой функции
.
Функция
,

Слайд 4Одним из возможных критериев величины этой разности является интеграл от

квадрата разности колебания и его разложения:
Если для непрерывной функции s(t)

Слайд 5Для определения коэффициентов cn, обеспечивающих минимум Δ, умножим обе части

(1.4) на и произведем интегрирование:
В силу свойств ортогональности в правой

Слайд 6Разложение периодических колебаний в ряд Фурье
по системе тригонометрических функций

(1.7)

Слайд 7

или

(1.8)
(1.9)

Слайд 8Ряд Фурье в комплексной форме

Положим α = nω1t +

θn и обозначим

Эту величину назовем комплексной амплитудой n-й гармоники.
Она

Слайд 9После этого ряд (1.8) можно записать в таком виде:
где

- величина,

комплексно-сопряжённая

Комплексную амплитуду можно вычислить непосредственно

Слайд 10Формулы (1.12) и (1.13) можно называть парой преобразований Фурье.
Вторая из

них позволяет найти спектр, т. е. совокупность гармонических
составляющих, образующих в

Слайд 11Коэффициенты комплексного (а) и тригонометрического (б) рядов Фурье
периодической функции

времени

Слайд 12

Слайд 13

(1.13):

а)

Слайд 14
Рис. 3. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье
(1.13)

Слайд 15
б)
(1.14)

Слайд 16
(1.15)

Слайд 17
(1.16)

Слайд 18

(1.19)
(1.18)
(1.17)

Слайд 19

(1.20)

Слайд 20

(1.21)

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Энергетические характеристики и разложение в ряд

Содержание

Слайды и текст этой презентации

Слайд 1Энергетические характеристикиМгновенная мощность определяется как квадрат мгновенного значения s(t): Энергия сигнала

на интервале t2, t1 определяется как интеграл от мгновенной мощности:Отношениеимеет

Слайд 2Разложение колебаний по системам ортогональных функций удовлетворяет на некотором отрезке времени

(t1, t2) условиям Если совокупность функцийто ее называют системой ортогональных

Слайд 3 Заданное колебание можно разложить по системе ортогональных функций, если

можно записать и . (1.5)Величина называется нормой функции .Функция ,

Слайд 4Одним из возможных критериев величины этой разности является интеграл от

квадрата разности колебания и его разложения:Если для непрерывной функции s(t)

Слайд 5Для определения коэффициентов cn, обеспечивающих минимум Δ, умножим обе части

(1.4) на и произведем интегрирование:В силу свойств ортогональности в правой

Слайд 6Разложение периодических колебаний в ряд Фурьепо системе тригонометрических функций(1.7)

Слайд 7или(1.8)(1.9)

Слайд 8Ряд Фурье в комплексной форме Положим α = nω1t +

θn и обозначим Эту величину назовем комплексной амплитудой n-й гармоники.Она

Слайд 9После этого ряд (1.8) можно записать в таком виде:где- величина,

комплексно-сопряжённая Комплексную амплитуду можно вычислить непосредственно

Слайд 10Формулы (1.12) и (1.13) можно называть парой преобразований Фурье.Вторая из

них позволяет найти спектр, т. е. совокупность гармоническихсоставляющих, образующих в

Слайд 11Коэффициенты комплексного (а) и тригонометрического (б) рядов Фурье периодической функции

времени

Слайд 12

Слайд 13(1.13):а)

Слайд 14Рис. 3. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье(1.13)

Слайд 15б)(1.14)

Слайд 16(1.15)

Слайд 17(1.16)

Слайд 18(1.19)(1.18)(1.17)

Слайд 19(1.20)

Слайд 20(1.21)

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Энергетические характеристики
Мгновенная мощность определяется как квадрат мгновенного значения s(t):

Энергия сигнала

на интервале t2, t1 определяется как интеграл от мгновенной мощности:

Отношение

имеет

Слайд 2Разложение колебаний по системам ортогональных функций

удовлетворяет на некотором отрезке времени

(t1, t2) условиям

Если совокупность функций

то ее называют системой ортогональных

Слайд 3

Заданное колебание можно разложить по системе ортогональных функций, если

можно записать
и
.
(1.5)

Величина
называется нормой функции
.
Функция
,

квадрата разности колебания и его разложения:
Если для непрерывной функции s(t)

(1.4) на и произведем интегрирование:
В силу свойств ортогональности в правой

Слайд 6Разложение периодических колебаний в ряд Фурье
по системе тригонометрических функций

(1.7)

Слайд 7

или

(1.8)
(1.9)

Слайд 8Ряд Фурье в комплексной форме

Положим α = nω1t +

θn и обозначим

Эту величину назовем комплексной амплитудой n-й гармоники.
Она

Слайд 9После этого ряд (1.8) можно записать в таком виде:
где

- величина,

комплексно-сопряжённая

Комплексную амплитуду можно вычислить непосредственно

Слайд 10Формулы (1.12) и (1.13) можно называть парой преобразований Фурье.
Вторая из

них позволяет найти спектр, т. е. совокупность гармонических
составляющих, образующих в

Слайд 11Коэффициенты комплексного (а) и тригонометрического (б) рядов Фурье
периодической функции

Слайд 13

(1.13):

а)

Слайд 14
Рис. 3. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье
(1.13)

Слайд 15
б)
(1.14)

Слайд 16
(1.15)

Слайд 17
(1.16)

Слайд 18

(1.19)
(1.18)
(1.17)

Слайд 19

(1.20)

Слайд 20

(1.21)