Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Филатов Александр Юрьевич (Главный научный сотрудник, доцент ШЭМ
Содержание
- 1. Филатов Александр Юрьевич (Главный научный сотрудник, доцент ШЭМ
- 2. Нелинейные модели, поддающиесянепосредственной линеаризации2Часто зависимость между y
- 3. Гиперболические зависимости3Гипербола смещенная по вертикали.Случай А. 0
- 4. Экспоненциальные зависимости4Постоянный темп относительного прироста во времени.5%
- 5. Логарифмические зависимости5Самая медленно растущая из неограни-ченных функций.Обратная
- 6. Степенные зависимости6Функция с постоянной эластичностью.Возможна множественная регрессия.j
- 7. Численный пример7Взаимосвязь реального обменного курса y (во
- 8. Выбор вида зависимости.Метод проб и ошибок8Задача: выбрать
- 9. Метод Бокса-Кокса9Метод Бокса-Кокса – автоматическая процедура подбора
- 10. Виды зависимостейв методе Бокса-Кокса10* = 1 –
- 11. Оценивание *.Решетчатая процедура111. Задаем интервал *[min; max],
- 12. Численный пример12Объем предложения акций на фондовом рынке y в зависимости от цены x
- 13. Численный пример13Объем предложения акций на фондовом рынке y в зависимости от цены x
- 14. Бинарныерезультирующие показатели14## Возраст, образование, стаж, желаемая зарплата
- 15. Логит- и пробит-модели15Наибольшее распространение получили две модели,
- 16. Практическая реализацияЛогит- и пробит-моделей16Нужно сделать переход от
- 17. Численный пример.Логит-модель17Доля владельцев автомобилей p в зависимости от среднедушевого дохода (x., тыс. руб./мес.)
- 18. Численный пример.Пробит-модель18Доля владельцев автомобилей p в зависимости от среднедушевого дохода (x., тыс. руб./мес.)
- 19. Спасибоза внимание!19alexander.filatov@gmail.comhttps://vk.com/alexander.filatov, https://vk.com/baikalreadingshttps://youtube.com/alexanderfilatov
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Филатов Александр Юрьевич
(Главный научный сотрудник, доцент ШЭМ ДВФУ)
Эконометрика-1
Лекции 5.1-5.2
Нелинейные модели.
Логит-
и пробит-модели
Слайд 2Нелинейные модели, поддающиеся
непосредственной линеаризации
2
Часто зависимость между y и регрессором х
может носить нелинейный или даже немонотонный характер. При этом для
их оценивания нужен тот же самый инструментарий, включая функцию ЛИНЕЙН в Excel.Полиномиальные зависимости
Вводим дополнительные переменные x(2)=x2, x(3)=x3,…, оцениваем модель обычным МНК.
Замечание 1. Схема работает для любого числа нелинейно воздействую-щих на результат переменных.
Замечание 2. Самый простой способ учесть немонотонное воздействие фактора, эффект насыщения и т.д.
Замечание 3. Не следует прибегать к высоким степеням. Линейный член – рост, квадратичный – ускорение, кубичный – ???
## Темпы роста инфляции стали сокращаться.
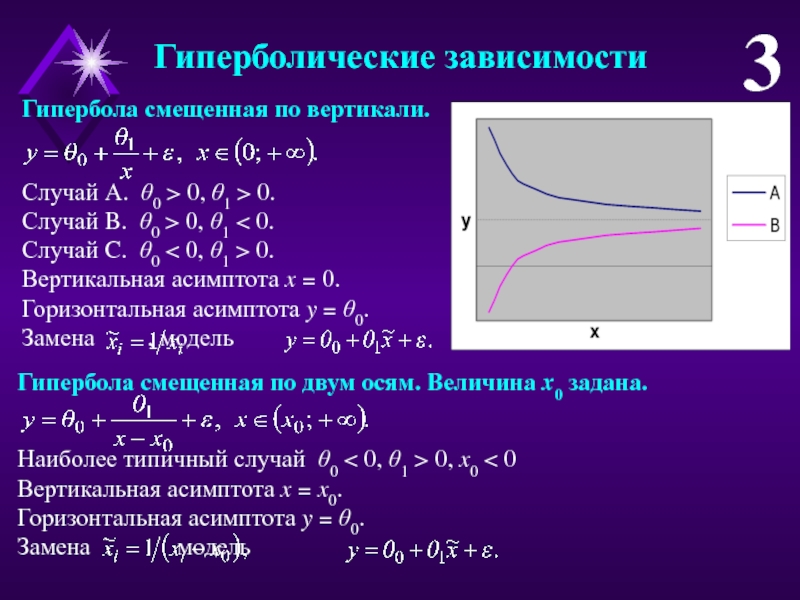
Слайд 3Гиперболические зависимости
3
Гипербола смещенная по вертикали.
Случай А. 0 > 0, 1
> 0.
Случай B. 0 > 0, 1 < 0.
Случай C.
0 < 0, 1 > 0.Вертикальная асимптота x = 0.
Горизонтальная асимптота y = 0.
Замена , модель
Гипербола смещенная по двум осям. Величина x0 задана.
Наиболее типичный случай 0 < 0, 1 > 0, x0 < 0
Вертикальная асимптота x = x0.
Горизонтальная асимптота y = 0.
Замена модель
Слайд 4Экспоненциальные зависимости
4
Постоянный темп относительного прироста во времени.
5% / год =
132 раза / век, 10% / год = 13781 раз
/ век.0 – начальный уровень,
1 – темп прироста.
Случай А. 1 > 0 – рост.
Случай B. 1 < 0 - спад.
Замена
Модель
Логистическая зависимость.
Горизонтальные асимптоты y = 0 и y = 1/0.
Пересечение оси в точке y = 1/(0+1)
Замена
Модель
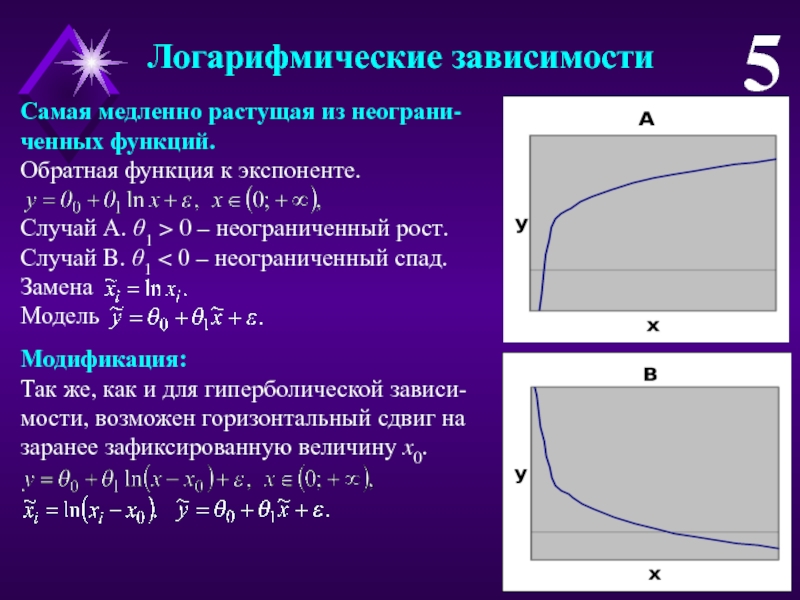
Слайд 5Логарифмические зависимости
5
Самая медленно растущая из неограни-ченных функций.
Обратная функция к экспоненте.
Случай
А. 1 > 0 – неограниченный рост.
Случай B. 1
0 – неограниченный спад.Замена
Модель
Модификация:
Так же, как и для гиперболической зависи-мости, возможен горизонтальный сдвиг на заранее зафиксированную величину x0.
Слайд 6Степенные зависимости
6
Функция с постоянной эластичностью.
Возможна множественная регрессия.
j – эластичности y
по x(j).
Замена
Модель
Различие монотонных функций:
Экспонента – линейна в логарифмических ко-ординатах,
растет быстрее всех функций.Степень – линейна в двойных логарифмичес-ких координатах, растет быстрее полинома.
Логарифм – растет медленнее всех функций!
Закон Зипфа:
Многие экономические показатели (размеры городов, фирм, доходы богатых людей и т.д. распределены по степенном закону!
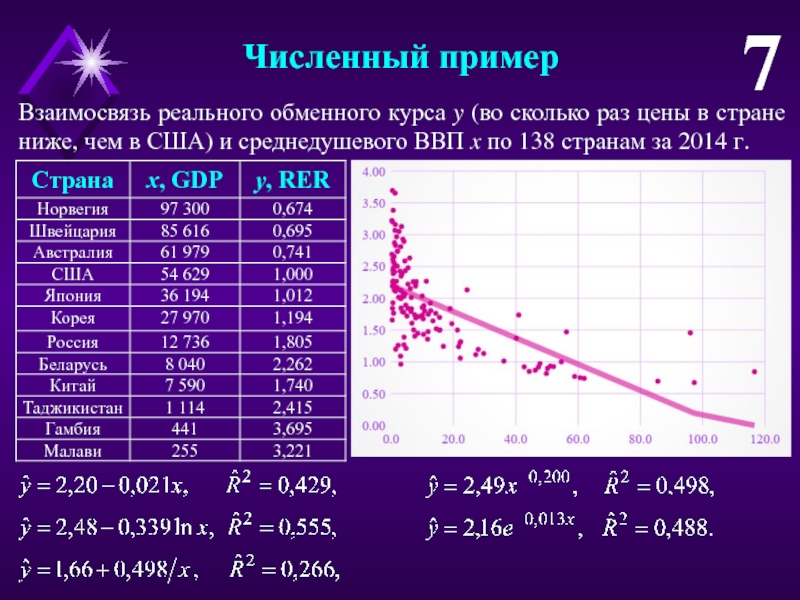
Слайд 7Численный пример
7
Взаимосвязь реального обменного курса y (во сколько раз цены
в стране ниже, чем в США) и среднедушевого ВВП x
по 138 странам за 2014 г.Слайд 8Выбор вида зависимости.
Метод проб и ошибок
8
Задача: выбрать из всевозможных видов
моделей наилучшую.
Построить различные варианты моделей (полиномиальные, гипербо-лические, экспоненциальные, логарифмические, степенные
и т.д.).Оценить модели (найти значения всех коэффициентов).
Выбрать наилучшую из моделей, учитывая значение коэффициента детерминации, а также число оцениваемых параметров.
Двухкритериальная задача:
Максимизируем значение коэффициента детерминации, одновремен-но сокращая число оцениваемых параметров модели.
Замечание 1. Иногда максимизируют несмещенную оценку R2:
Замечание 2. Если y входит в модель линейно (только в этом случае!), можем использовать оценку R2, которую дает функция ЛИНЕЙН.
Замечание 3. Можем учесть значимость регрессоров и другие факторы.
Слайд 9Метод Бокса-Кокса
9
Метод Бокса-Кокса – автоматическая процедура подбора линеаризу-ющего преобразования:
Гипотеза: существует
значение *, такое что
или
Замечание. Преобразования применяются исключительно к положи-тельным переменным.
Если для некоторой переменной имеются отрица-тельные значения, осуществляется сдвиг:Слайд 10Виды зависимостей
в методе Бокса-Кокса
10
* = 1 – линейная зависимость y
от x(1),…,x(p).
* = 0 – степенная или экспоненциальная зависимость y
от x(1),…,x(p):При других значениях * получаем связь некоторых степеней исходных переменных:
## * = 0,5,
Слайд 11Оценивание *.
Решетчатая процедура
11
1. Задаем интервал *[min; max], часто *[–1; 2].
2.
С некоторым шагом
1) Вычисляем значения
и, при необходимости2) Находим оценки коэффициентов линейной регрессии
3) Вычисляем коэффициент детерминации
3. Строим зависимость и находим
4. Переходим в исходные координаты y(x) и строим прогноз.
Замечание 1. При практической реализации решетчатой процедуры можно сначала оценить значение * достаточно грубо, используя то, что при (–; *) монотонно возрастает, а при (*; +) – убы-вает. Можно также использовать методы одномерной оптимизации.
Замечание 2. На некоторых практических задачах оптимальное значе-ние * находится вне интервала [–1; 2].
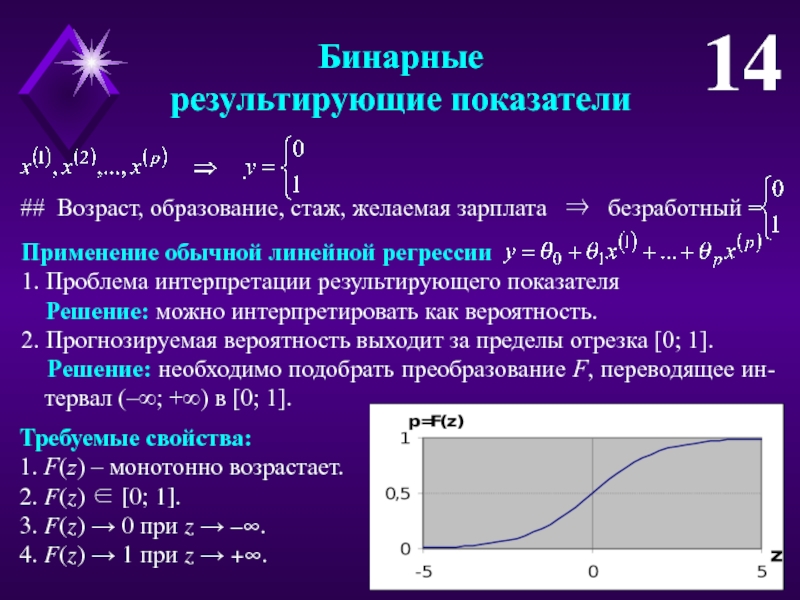
Слайд 14Бинарные
результирующие показатели
14
## Возраст, образование, стаж, желаемая зарплата
безработный =
Применение обычной линейной регрессии
1. Проблема интерпретации результирующего показателя
Решение: можно интерпретировать как вероятность.2. Прогнозируемая вероятность выходит за пределы отрезка [0; 1].
Решение: необходимо подобрать преобразование F, переводящее ин-тервал (–; +) в [0; 1].
Требуемые свойства:
1. F(z) – монотонно возрастает.
2. F(z) [0; 1].
3. F(z) → 0 при z → –.
4. F(z) → 1 при z → +.
Слайд 15Логит- и пробит-модели
15
Наибольшее распространение получили две модели, основанные на сле-дующих
преобразующих функциях:
1. Логит-модель
Использует логистическую функцию
2. Пробит-модель:
Использует функцию распределения нормального стандартного закона. Замечание:
Обе функции симметричны относительно z = 0 и в целом очень похожи по конфигурации.
Пробит-модель демонстрирует чуть более быстрое стремление вероятно-сти к нулю и единице при высоких и низких значениях z.
Слайд 16Практическая реализация
Логит- и пробит-моделей
16
Нужно сделать переход от индивидуальных наблюдений к
частотам, поэ-тому для оценивания необходимы повторяющиеся исходные данные.
Вариант 1. Несколько
наблюдений для каждого значения x.Вариант 2. Несколько наблюдений для каждого интервала группировки:
– относительная частота появ-ления единиц для j-значения X
Логит-модель:
Пробит-модель:
находим МНК-оценки коэффициентов
при необходимости учитываем гетероскедастичность







![Филатов Александр Юрьевич
(Главный научный сотрудник, доцент ШЭМ Оценивание *.Решетчатая процедура111. Задаем интервал *[min; max], часто *[–1; 2].2. С Оценивание *.Решетчатая процедура111. Задаем интервал *[min; max], часто *[–1; 2].2. С некоторым шагом 1) Вычисляем](/img/thumbs/e6fd87a7b1b534c70bf3afb80b6d55a7-800x.jpg)