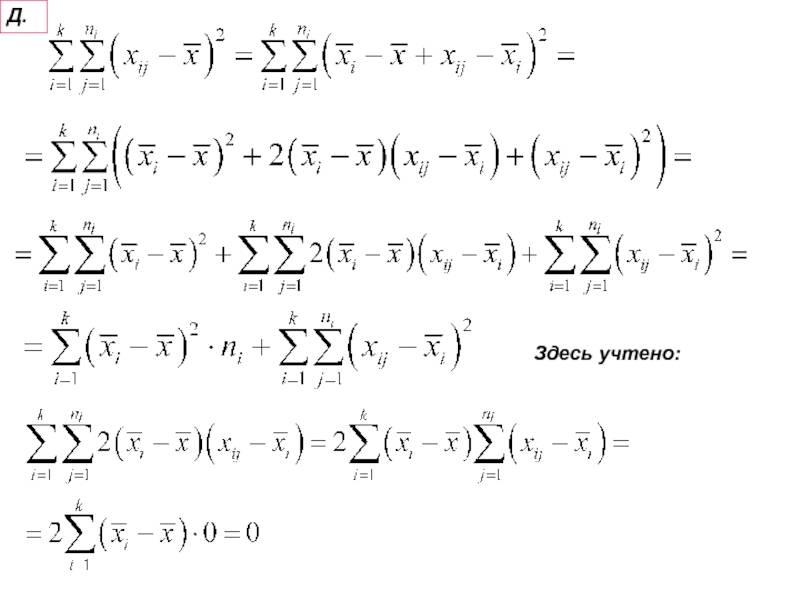Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6 1.Постановка задач дисперсионного анализа 2.Однофакторная
Содержание
- 1. Лекция 6 1.Постановка задач дисперсионного анализа 2.Однофакторная
- 2. Задача дисперсионного анализа заключается в выделении и
- 3. Примеры задачОценить:- влияние количества удобрений на урожайность
- 4. (6.1)Фактор А фиксируется на k
- 5. Рассмотрим примеры:Количество внесённых удобрений: 10; 20;30 единицКоличество
- 6. 3.Основное тождество дисперсионного анализаФактор фиксируется на k
- 7. - объем выборки 1. Формулируется нулевая гипотеза:«влияние
- 8. Суммы квадратов отклонений:- общая сумма квадратов Сумма
- 9. Здесь учтено:Д.
- 10. 4. Статистический критерийРассмотрим выборочные дисперсии:- факторная дисперсия- остаточная дисперсия(6.9)(6.10)
- 11. Теорема. Если верна нулевая гипотеза, то случайная
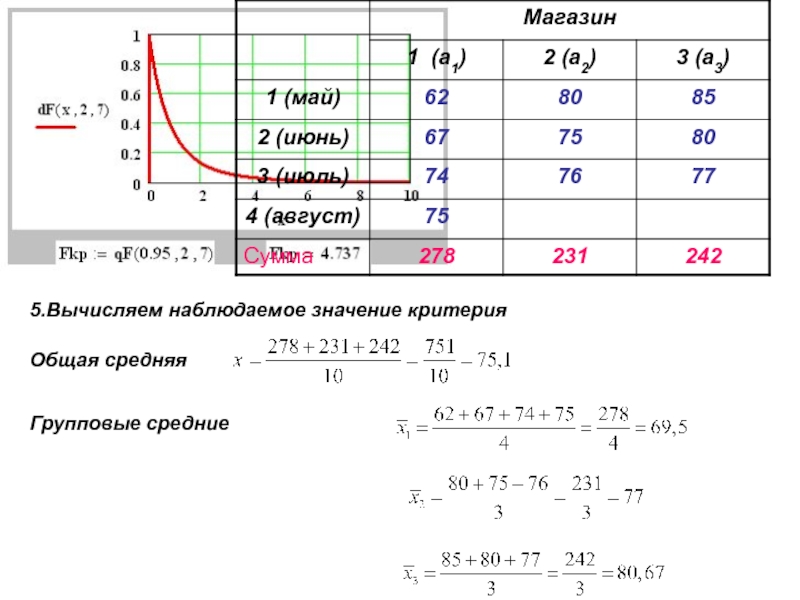
- 12. Пример. В трех магазинах продаются
- 13. Пусть Х – товарооборот в у.е. за
- 14. 5.Вычисляем наблюдаемое значение критерияОбщая средняяГрупповые средние
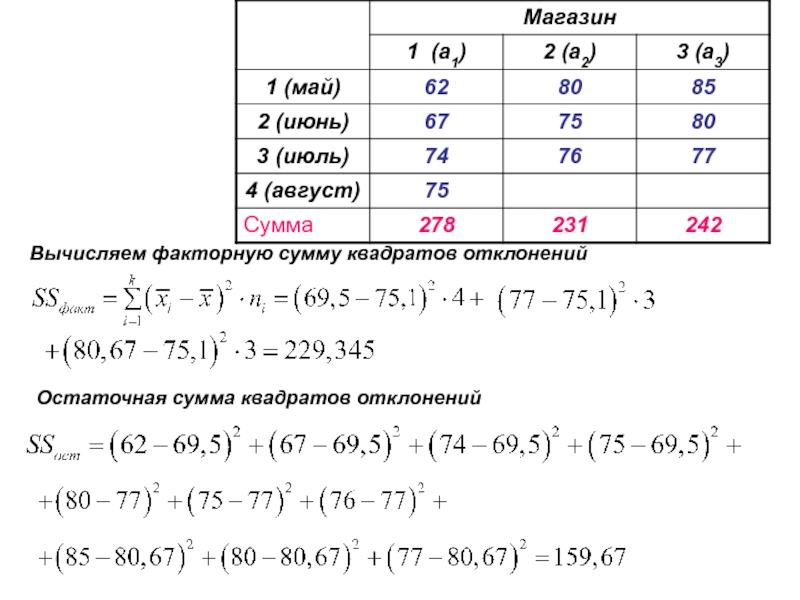
- 15. Вычисляем факторную сумму квадратов отклоненийОстаточная сумма квадратов отклонений
- 16. Остаточная дисперсияН0 отвергается. Влияние фактора А следует считать значимымФакторная дисперсия
- 17. Скачать презентанцию
Задача дисперсионного анализа заключается в выделении и оценке отдельных факторов, вызывающих изменчивость величины. Дисперсионный анализ разработал английский статистик Фишер для анализа результатов обработки агрономических опытов в 1918
Слайды и текст этой презентации
Слайд 1Лекция 6
1.Постановка задач дисперсионного анализа
2.Однофакторная дисперсионная модель. Основные предположения
3.Основное
тождество дисперсионного анализа
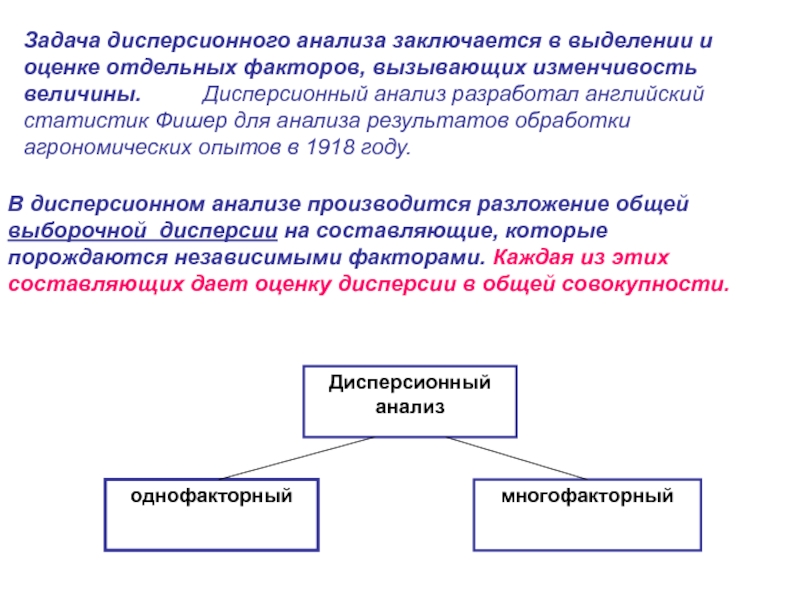
назначение дисперсионного анализа определил следующим образом: «отделение дисперсии, приписываемой одной группе причин, от дисперсии, приписываемой другим группам». 
Слайд 2Задача дисперсионного анализа заключается в выделении и оценке отдельных факторов,
вызывающих изменчивость величины. Дисперсионный анализ разработал
английский статистик Фишер для анализа результатов обработки агрономических опытов в 1918 году.В дисперсионном анализе производится разложение общей выборочной дисперсии на составляющие, которые порождаются независимыми факторами. Каждая из этих составляющих дает оценку дисперсии в общей совокупности.
Слайд 3Примеры задач
Оценить:
- влияние количества удобрений на урожайность культуры
- влияние объемов
инвестиций на прибыль предприятия
- влияние количества катализатора на скорость химической
реакции- влияние доз лекарственного препарата на концентрацию сахара в крови
влияние формы управления предприятием на товарооборот
- влияние различных режимов термообработки на свойства материала
2.Однофакторная дисперсионная модель. Основные предположения.
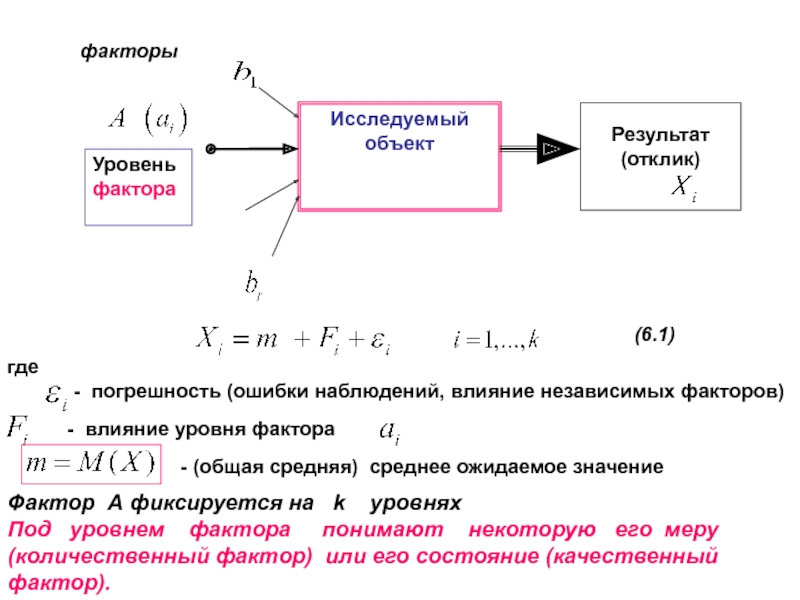
Слайд 4(6.1)
Фактор А фиксируется на k уровнях
Под уровнем
фактора понимают некоторую его меру
(количественный фактор) или его состояние (качественный фактор).где
- погрешность (ошибки наблюдений, влияние независимых факторов)
- влияние уровня фактора
- (общая средняя) среднее ожидаемое значение
факторы
Слайд 5Рассмотрим примеры:
Количество внесённых удобрений: 10; 20;30 единиц
Количество катализатора: 10;15;20 г.
Объем
инвестиций: 50000; 100000; 300000 у.е.
Форма управления: предприятие
1; предприятие 2; предприятие 3Организация технологического процесса:
линия А, линия В, линия С.
Рассмотрим основные предположения.
1.Погрешности
- (ошибки наблюдений) - взаимно независимы
2.
3.
Слайд 63.Основное тождество дисперсионного анализа
Фактор фиксируется на k уровнях и на
каждом уровне проводится серия опытов. Наблюдаемые значения признака представлены в
таблице
Слайд 7- объем выборки
1. Формулируется нулевая гипотеза:
«влияние фактора незначимо»
2.Принимаем
3.Рассмотрим
выбор статистического критерия
- общая (выборочная) средняя,
средняя
i -ой группы (групповая средняя), дисперсия групповая
(6.2)
(6.3)
(6.4)
Слайд 8Суммы квадратов отклонений:
- общая сумма квадратов
Сумма квадратов отклонений от
общей средней
факторная сумма квадратов отклонений
(результат влияния фактора А) или
межгрупповая сумма квадратов.остаточная сумма квадратов
(результат изменчивости случайной величины внутри группы)
Справедливо тождество
(6.5)
(6.6)
(6.7)
(6.8)
Слайд 104. Статистический критерий
Рассмотрим выборочные дисперсии:
- факторная дисперсия
- остаточная дисперсия
(6.9)
(6.10)
Слайд 11Теорема. Если верна нулевая гипотеза, то случайная величина
имеет распределение Фишера
с параметрами
и
Замечание. Справедливы формулы:
и
являются несмещенными оценками дисперсии
Если верна нулевая
гипотеза, тоПроверка нулевой гипотезы сводится к проверке существенности различия выборочных дисперсий
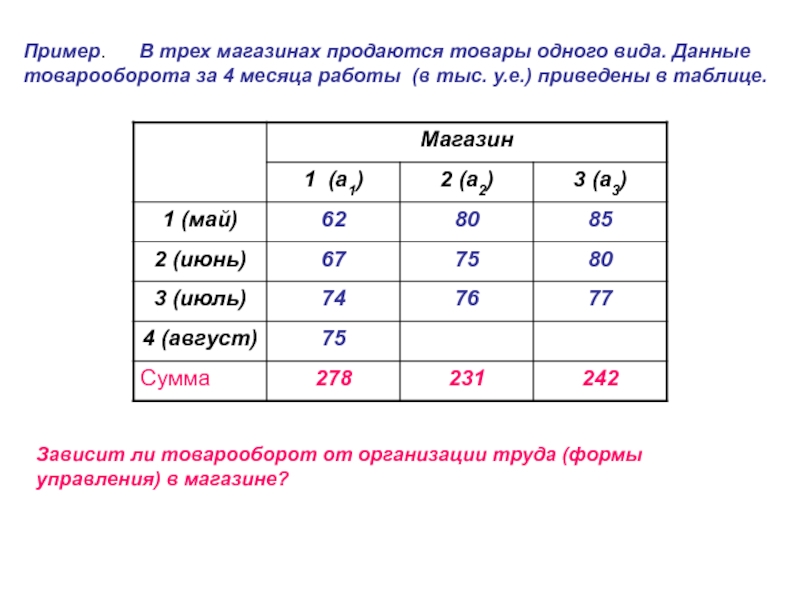
Слайд 12Пример. В трех магазинах продаются товары одного вида.
Данные товарооборота за 4 месяца работы (в тыс. у.е.) приведены
в таблице.Зависит ли товарооборот от организации труда (формы управления) в магазине?
Слайд 13Пусть Х – товарооборот в у.е. за один месяц
H0: m1=m2=m3=m
(влияние фактора незначимо)
H1: (влияние фактора значимо)
2.
Принимаем3.Статистический критерий
Если верна нулевая гипотеза, то статистический критерий имеет распределение Фишера с параметрами
4.Определяем критическую область:
Слайд 16Остаточная дисперсия
Н0 отвергается. Влияние фактора А следует считать значимым
Факторная дисперсия
