Слайд 1Физические основы механики
Иванова Дарья 1Пи1
Слайд 2Тема: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА
1. Динамика вращательного движения твердого тела
относительно точки
2. Динамика вращательного движения твердого
тела относительно оси
3. Расчет моментов инерции некоторых простых тел. Теорема Штейнера
4. Кинетическая энергия вращающегося тела
5. Закон сохранения момента импульса
6. Законы сохранения и их связь с симметрией
пространства и времени
7. Сходство и различие линейных и угловых характеристик движения
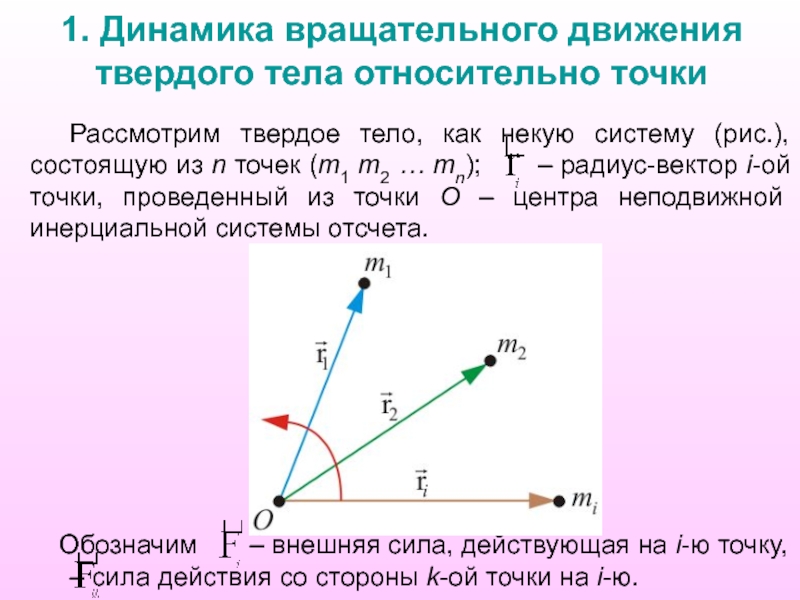
Слайд 31. Динамика вращательного движения твердого тела относительно точки
Рассмотрим твердое тело,
как некую систему (рис.), состоящую из n точек (m1 m2
… mn); – радиус-вектор i-ой точки, проведенный из точки О – центра неподвижной инерциальной системы отсчета.
Обозначим – внешняя сила, действующая на i-ю точку, – сила действия со стороны k-ой точки на i-ю.
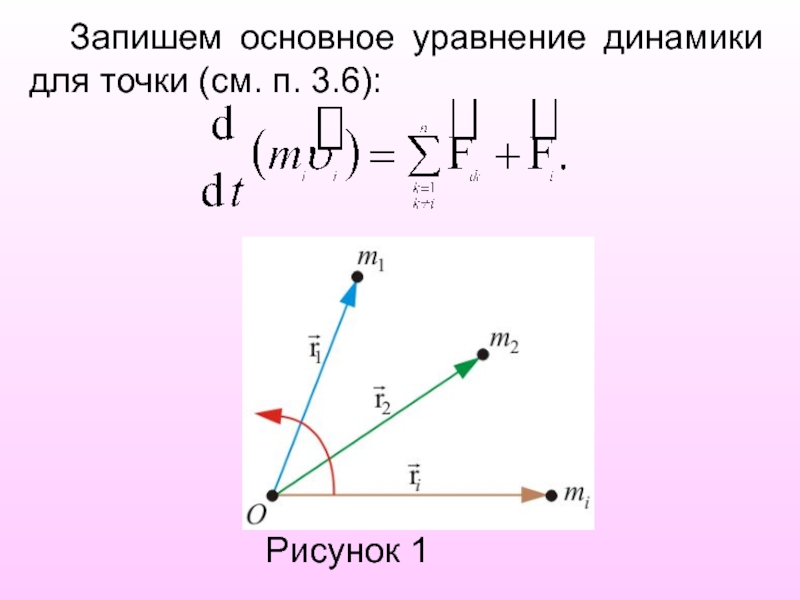
Слайд 4 Запишем основное уравнение динамики для точки (см. п. 3.6):
Рисунок 1
Слайд 5Умножим обе части векторно на
Знак производной можно вынести за
знак векторного произведения (и знак суммы тоже), тогда:
Слайд 6 Векторное произведение точки на её импульс называется
моментом импульса этой точки относительно точки О.
(1.1)
Эти три вектора образуют правую тройку векторов, связанных «правилом буравчика»:
Рисунок 2
Слайд 7 Векторное произведение
проведенного
в точку приложения сил, на эту силу называется моментом силы
(1.2)
Обозначим li – плечо силы Fi, (рис.3). Т.к
то:
(1.3)
Рисунок 3
Слайд 8C учетом новых обозначений:
(1.4)
Запишем систему n уравнений для
всех точек системы и сложим, левые и правые части уравнений:
Так
как
то
Слайд 9 Здесь сумма производных равна производной суммы:
где – момент
импульса системы,
– результирующий момент всех внешних сил относительно точки О.
Окончательно получим:
Слайд 10 Основной закон динамики вращательного движения твердого тела, вращающегося вокруг точки.
Момент
импульса системы является основной динамической характеристикой вращающегося
тела.
Сравнивая это уравнение с основным уравнением динамики поступательного движения, мы видим их внешнее сходство
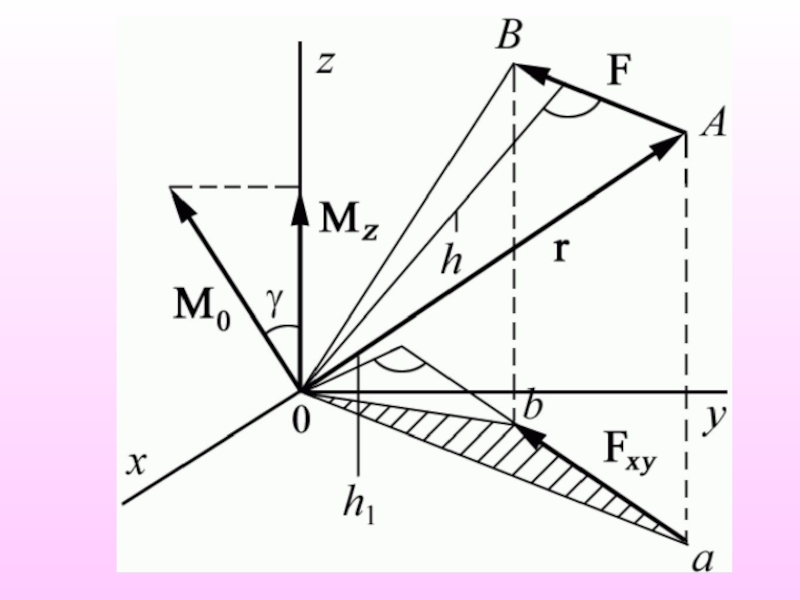
Слайд 12Или L = [r,p]
Здесь L трехмерный момент импульса
относительно центра вращения О.
Слайд 132. Динамика вращательного движения твердого тела
относительно оси
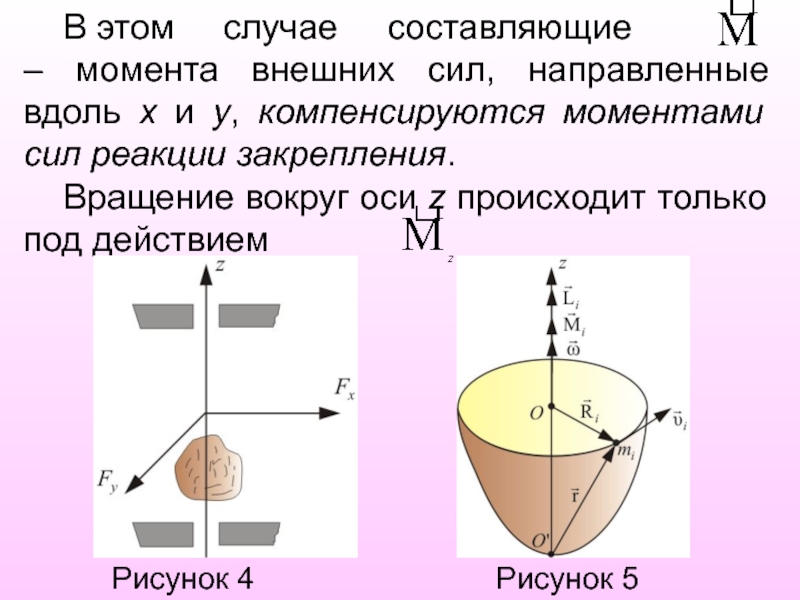
Слайд 14 В этом случае составляющие
– момента
внешних сил, направленные вдоль x и y, компенсируются моментами сил
реакции закрепления.
Вращение вокруг оси z происходит только под действием
Рисунок 4 Рисунок 5
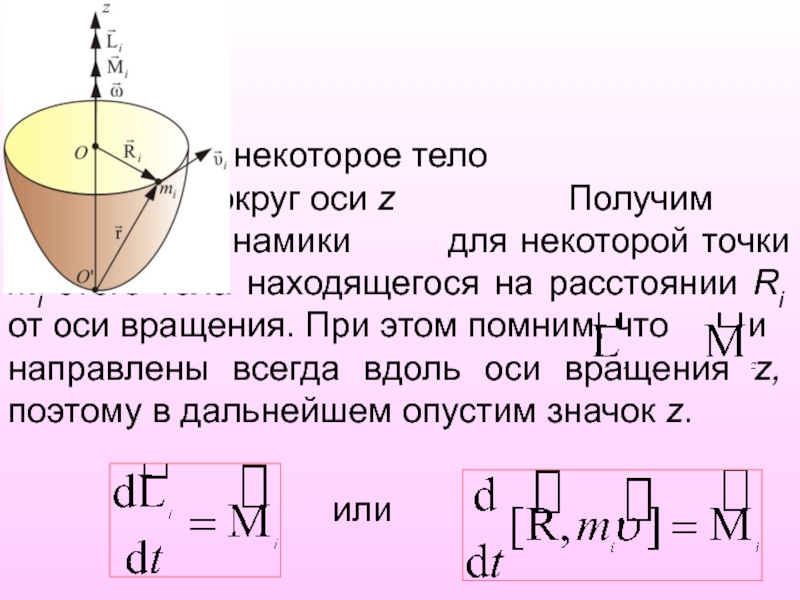
Слайд 15 Пусть некоторое тело вращается вокруг оси z Получим уравнение динамики
для некоторой точки mi этого тела находящегося на расстоянии Ri
от оси вращения. При этом помним, что и
направлены всегда вдоль оси вращения z, поэтому в дальнейшем опустим значок z.
или
Слайд 16 Так как у всех точек разная,
введем,
вектор угловой скорости причем
Тогда
Так как
тело абсолютно твердое, то в процессе вращения mi и Ri останутся неизменными. Тогда:
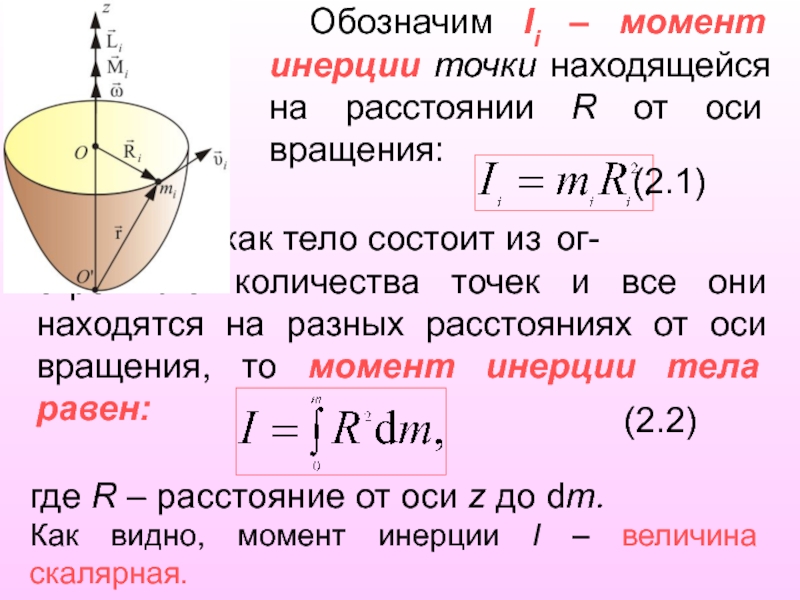
Слайд 17 Обозначим Ii – момент инерции точки находящейся на расстоянии R
от оси вращения:
(2.1)
Так как тело состоит из ог- огромного
количества точек и все они находятся на разных расстояниях от оси вращения, то момент инерции тела равен:
(2.2)
где R – расстояние от оси z до dm.
Как видно, момент инерции I – величина скалярная.
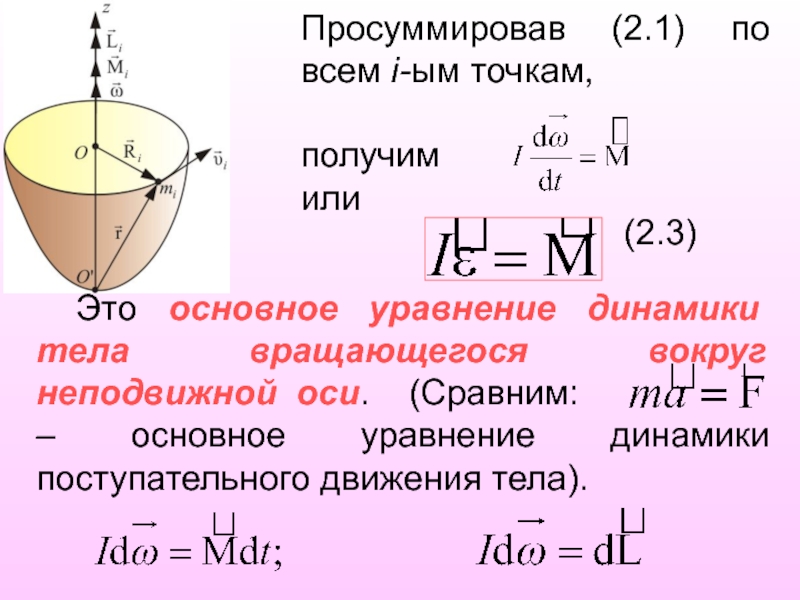
Слайд 18Просуммировав (2.1) по всем i-ым точкам,
получим
или
(2.3)
Это основное уравнение динамики тела вращающегося вокруг неподвижной оси. (Сравним:
– основное уравнение динамики поступательного движения тела).
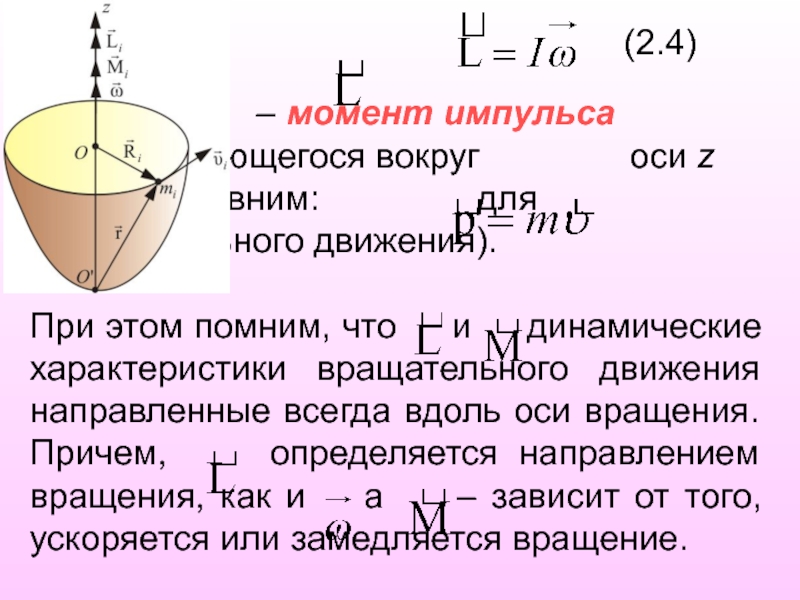
Слайд 19 (2.4)
Где – момент импульса тела вращающегося вокруг
оси z
(Сравним: для
поступательного движения).
При этом помним, что и динамические характеристики вращательного движения направленные всегда вдоль оси вращения. Причем, определяется направлением вращения, как и а – зависит от того, ускоряется или замедляется вращение.
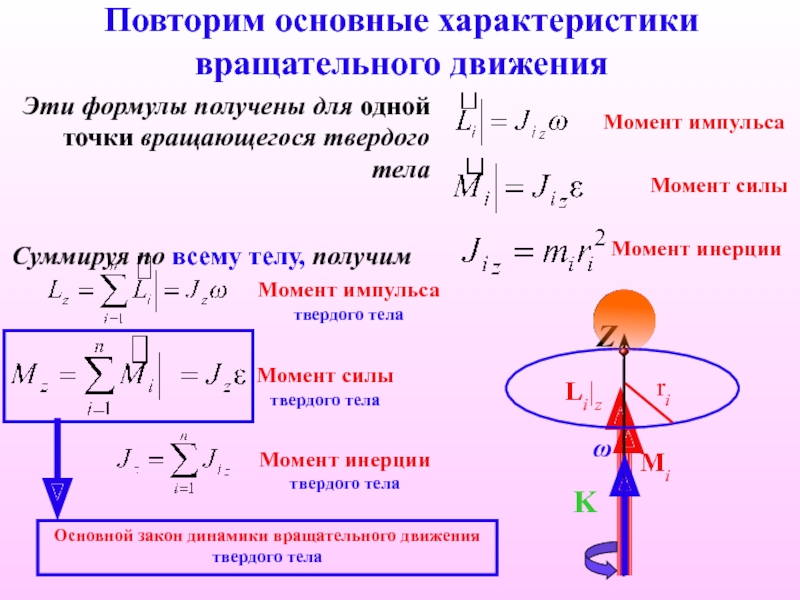
Слайд 20Повторим основные характеристики вращательного движения
Момент импульса
Эти формулы получены для одной
точки вращающегося твердого тела
Суммируя по всему телу, получим
Момент силы
Li|z
Mi
Момент инерции
Момент
импульса твердого тела
Момент силы твердого тела
Момент инерции твердого тела
Основной закон динамики вращательного движения твердого тела
Z
K
ω
ri
Слайд 213. Расчет моментов инерции некоторых простых тел.
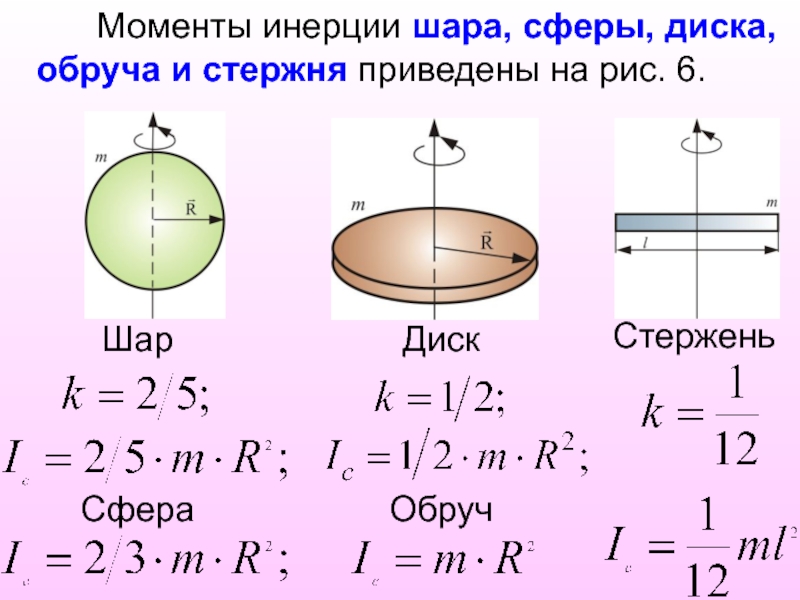
Слайд 22 Моменты инерции шара, сферы, диска, обруча и
стержня приведены на рис. 6.
Шар
Сфера
Диск
Обруч
Стержень
Слайд 23X
Y
Z
K
ri
ω
ε
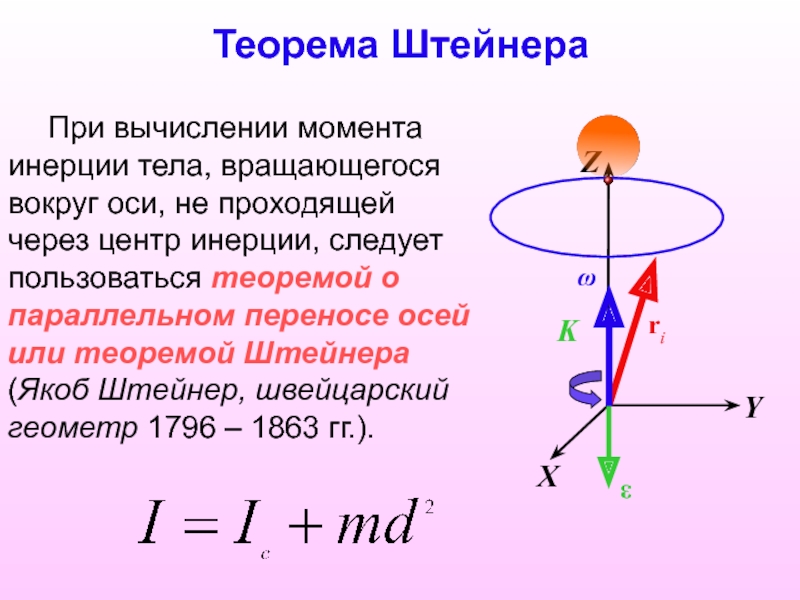
При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей
через центр инерции, следует пользоваться теоремой о параллельном переносе осей
или теоремой Штейнера (Якоб Штейнер, швейцарский геометр 1796 – 1863 гг.).
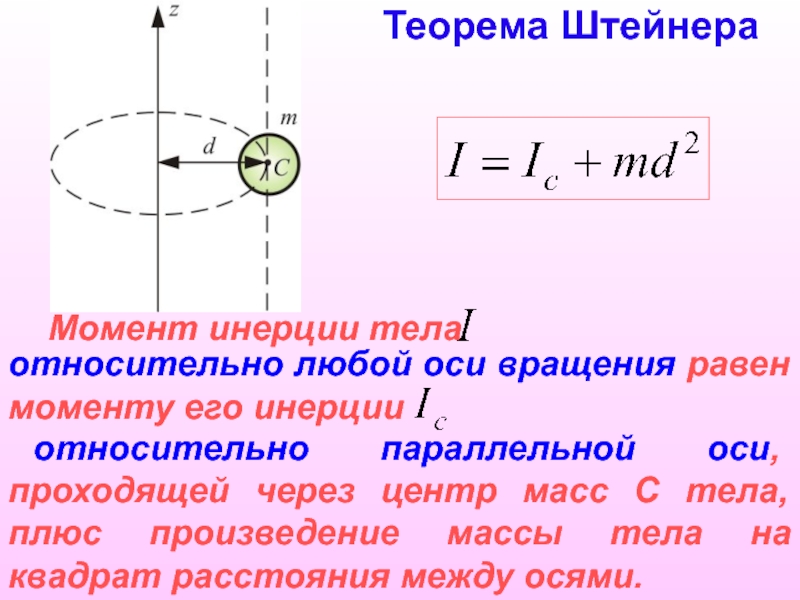
Теорема Штейнера
Слайд 24
Момент инерции тела
относительно любой оси вращения равен моменту его
инерции
относительно параллельной оси, проходящей через центр масс С
тела, плюс произведение массы тела на квадрат расстояния между осями.
Теорема Штейнера
Слайд 25 Пример: стержень массой m, длиной l, вращается вокруг оси,
проходящей через конец стержня (рис).
Слайд 264. Кинетическая энергия вращающегося тела
Слайд 27 Если тело вращается вокруг неподвижной оси z с угловой скоростью
то линейная скорость i-й точки
Следовательно,
Сопоставив
(4.1) и (4.2) можно увидеть, что момент инерции тела I – является мерой инертности при вращательном движении. Так же как масса m – мера инерции при поступательном движении.
Слайд 28 В общем случае движение твердого тела можно представить в виде
суммы двух движений – поступательного со скоростью и
вращательного с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. Полная кинетическая энергия этого тела:
. (4.3)
Здесь Ic – момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.
Слайд 29Пример:Скорость центра масс обруча равна v, масса обруча m. Определим
его кинетическую энергию при движении по горизонтальной поверхности.
Имеем
Kполн =
+ ,
– линейная скорость обода.
Для наблюдателя,
движущегося вместе с центром
обруча, скорость точки
соприкосновения обруча с плоскостью
равна v. Поэтому = v.
Таким образом, Kполн = + = mv2.
Слайд 305. Закон сохранения момента импульса
Закон сохранения момента импульса
Слайд 31 Закон сохранения момента импульса – момент импульса замкнутой системы тел
относительно любой неподвижной точки не изменяется с течением времени.
Это один
из фундаментальных законов природы.
Аналогично для замкнутой системы вращающихся вокруг оси z:
отсюда
или
Слайд 32 Если момент внешних сил относительно неподвижной оси вращения тождественно равен
нулю, то момент импульса относительно этой оси не изменяется в
процессе движения.
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.
Рисунок 10
Используется
гироскоп в различных навигационных устройствах кораблей, самолетов, ракет (гирокомпас, гирогоризонт).
Уравновешенный гироскоп – быстро вращающееся тело, имеющее три степени свободы
Слайд 36 Именно закон сохранения момента импульса используется танцорами на льду для
изменения скорости вращения. Или еще известный пример – скамья Жуковского.
Изученные
нами законы сохранения есть следствие симметрии пространства – времени.
Принцип симметрии был всегда путеводной звездой физиков, и она их не подводила.
Но вот в 1956 г. Ву Цзянь, обнаружил асимметрию в слабых взаимодействиях:
Слайд 37он исследовал β – распад ядер изотопа Со60 в магнитном
поле и обнаружил, что число электронов, испускаемых вдоль направления магнитного
поля не равно числу электронов испускаемых в противоположенном направлении.
В этом же году Л. Ледерман и Р. Гарвин (США) обнаружили нарушение симметрии при распаде пионов и мюонов.
Эти факты означают, что законы слабого взаимодействия, не обладают зеркальной симметрией.
Слайд 38
6. Законы сохранения и их связь с симметрией
пространства и времени
Три
фундаментальных закона природы: закон сохранения импульса, момента импульса и энергии.
Следует понимать, что эти законы выполняются только в инерциальных системах отсчета. В самом деле, при выводе этих законов мы пользовались вторым и третьим законами Ньютона, а последние применимы только в инерциальных системах.
Слайд 39 Напомним также, что импульс и момент импульса сохраняются в том
случае, если систему можно считать замкнутой (сумма всех внешних сил,
и собственно, всех моментов сил, равна нулю). Для сохранения же энергии тела условия замкнутости недостаточно – тело должно быть еще и адиабатически изолированным (т.е. не участвовать в теплообмене).
Слайд 40 Во всей истории развития физики, законы сохранения оказались, чуть ли
не единственными законами, сохранившими свое значение при замене одних теорий
другими. Эти законы тесно связаны с основными свойствами пространства и времени.
Слайд 41 Равнозначность следует понимать в том смысле, что замена моментом времени
t1 на момент времени t2, без изменения значений координат и
скорости частиц не изменяет механические свойства системы. Это означает то, что после указанной замены, координаты и скорости частиц имеют в любой момент времен такие же значения, какие имели до замены, в момент времени
1. В основе закона сохранения энергии лежит однородность времени, т. е. равнозначность всех моментов времени (симметрия по отношению к сдвигу начала отсчета времени).
Слайд 42 2. В основе закона сохранения импульса лежит однородность пространства, т.
е. одинаковость свойств пространства во всех точках (симметрия по отношению
к сдвигу начала координат).
Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы.
Слайд 43 3. В основе закона сохранения момента импульса лежит изотропия пространства,
т. е. одинаковость свойств пространства по всем направлениям (симметрия по
отношению к повороту осей координат).
Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.
Слайд 44 Так, если задана сила, действующая на материальную точку и начальные
условия, то можно найти закон движения, траекторию, величину и направление
скорости в любой момент времени и т. п. Законы же сохранения не дают нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в природе не происходят.
Таким образом, законы сохранения проявляются как принципы запрета:
Между законами типа основного уравнения динамики и законами сохранения имеется принципиальная разница.
Законы динамики дают нам представление о детальном ходе процесса.
Слайд 45 Любое явление, при котором не выполняются хотя бы один из
законов сохранения, запрещено, и в природе такие явления никогда не
наблюдаются.
Всякое явление, при котором не нарушается ни один из законов сохранения, в принципе может происходить.
Рассмотрим следующий пример. Может ли покоящееся тело за счет внутренней энергии начать двигаться? Этот процесс не противоречит закону сохранения энергии. Нужно лишь, чтобы возникающая кинетическая энергия точно равнялась убыли внутренней энергии.
Принципы запрета:
Слайд 46 На самом деле такой процесс никогда не происходит, ибо он
противоречит закону сохранения импульса. Раз тело покоилось, то его импульс
был равен нулю. А если оно станет двигаться, то его импульс сам собой увеличится, что невозможно. Поэтому внутренняя энергия тела не может превратиться в кинетическую, если тело не распадётся на части.
Если же допустить возможность распада этого тела на части, то запрет, налагаемый законом сохранения импульса, снимается.
Слайд 47 При этом возникшие осколки могут двигаться так, чтобы их центр
масс оставался в покое, – а только этого и требует
закон сохранения импульса.
Итак, для того чтобы внутренняя энергия покоящегося тела могла превратиться в кинетическую, это тело должно распадаться на части. Если же есть еще один какой-либо закон, запрещающий распад этого тела на части, то его внутренняя энергия и масса покоя будут постоянными величинами.
Слайд 48 Фундаментальность законов сохранения заключается в их универсальности:
Они справедливы при
изучении любых физических процессов (механических, тепловых, электромагнитных, и др.).
Они
одинаково применимы в релятивистском и нерелятивистском движении,
в микромире, где справедливы квантовые представления
и в макромире.
Слайд 497. Сходство и различие линейных и угловых
характеристик движения
Формулы кинематики и
динамики вращательного движения легко запоминаются, если сопоставить их с формулами
поступательного движения (см. таблицу 6.1).
Слайд 50Поступательное движение Вращательное движение








![Физические основы механики Или L = [r,p]Здесь L трехмерный момент импульса относительно центра вращения О. Или L = [r,p]Здесь L трехмерный момент импульса относительно центра вращения О.](/img/thumbs/6985f4b6f60167f0ac64cfe7bef900a1-800x.jpg)