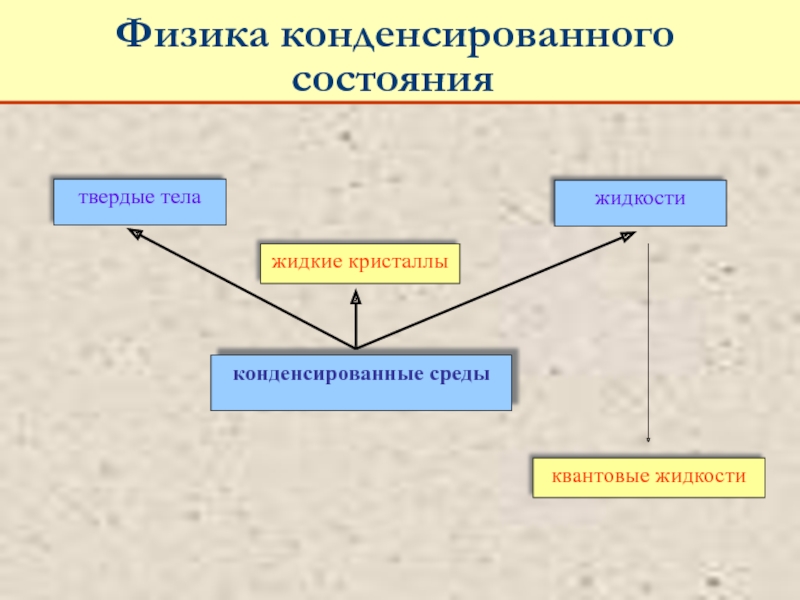
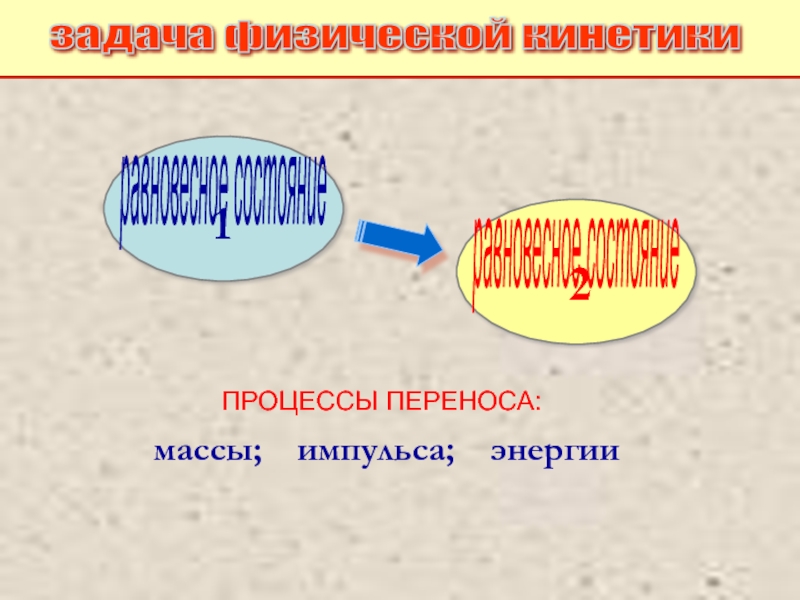
Физика конденсаторного состояния

Содержание

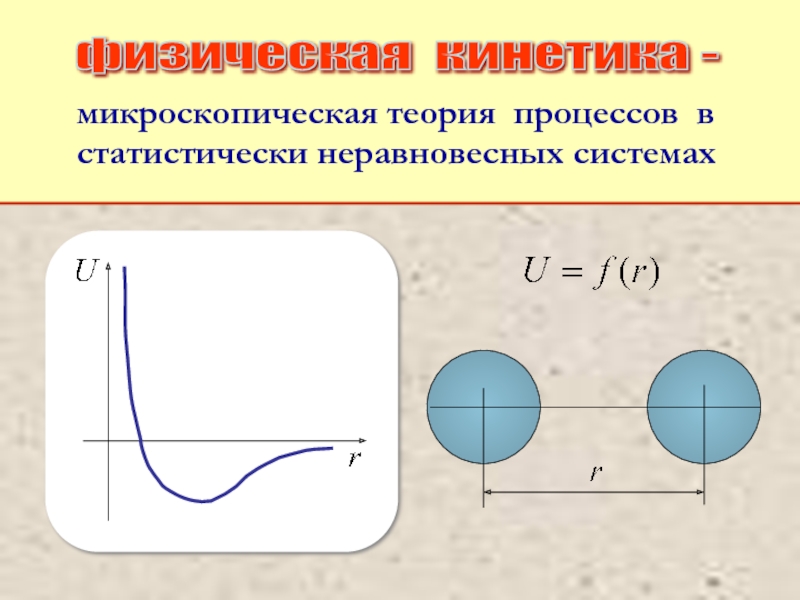
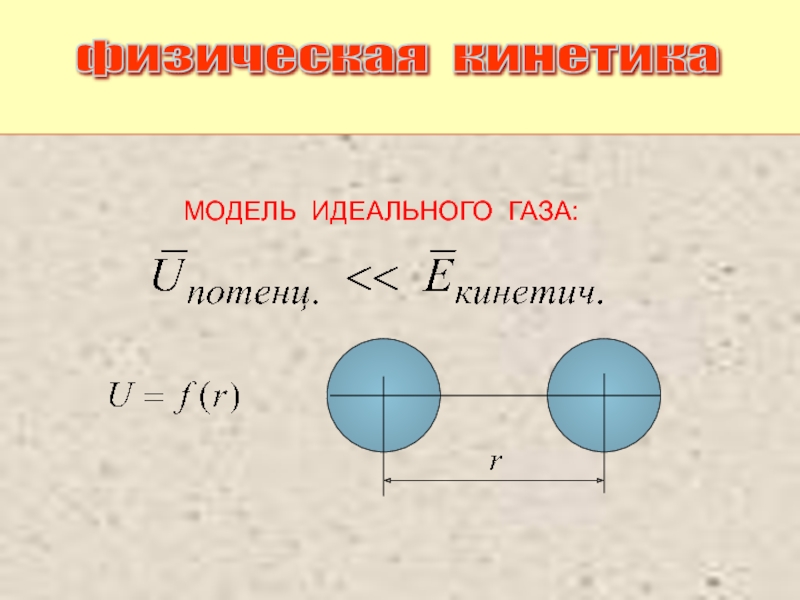
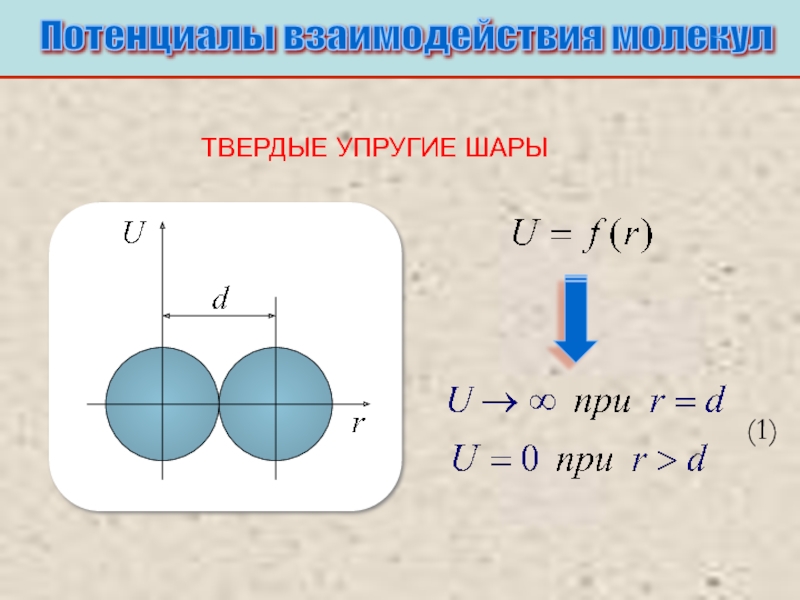
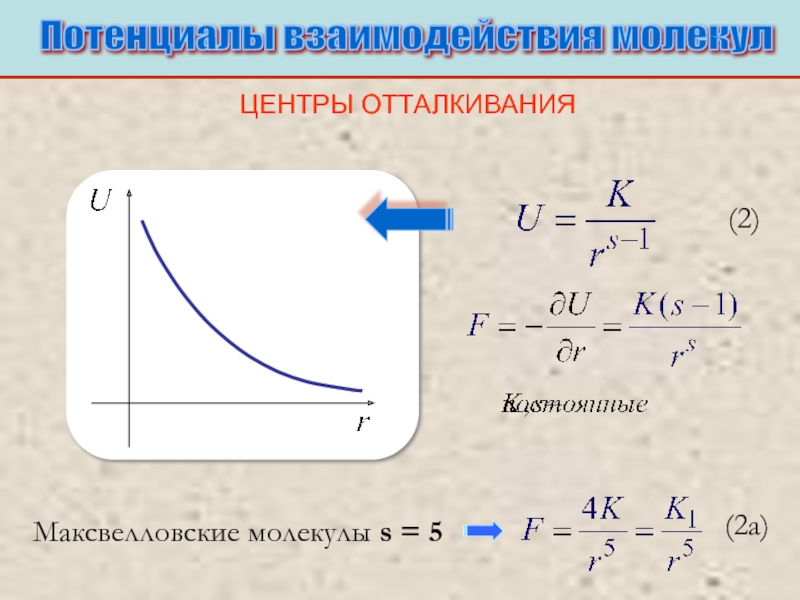
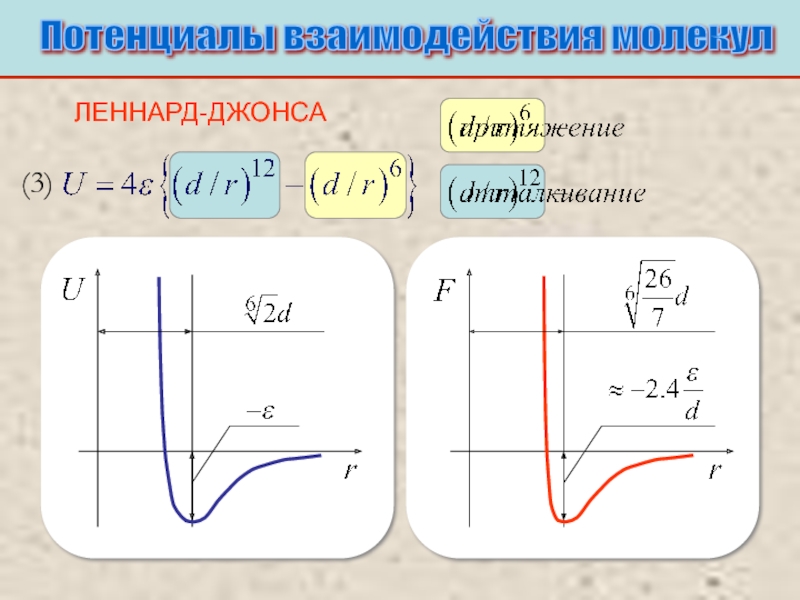
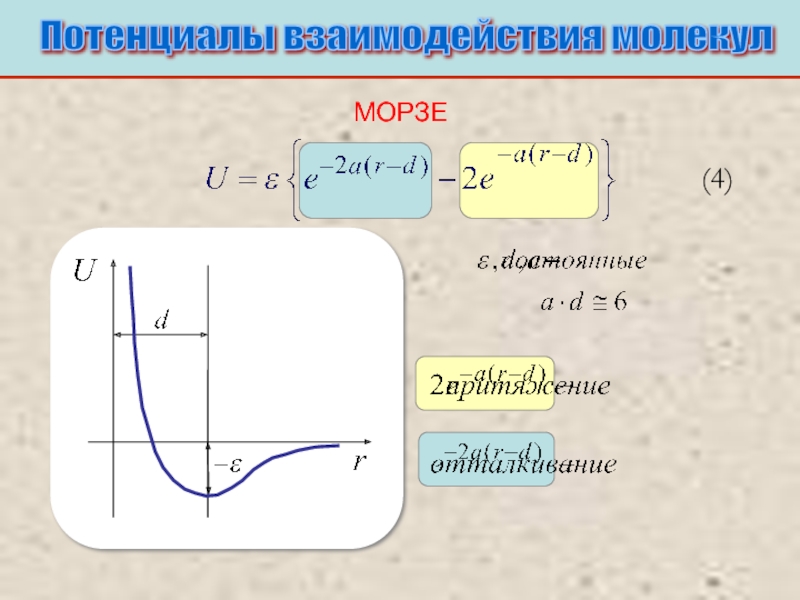
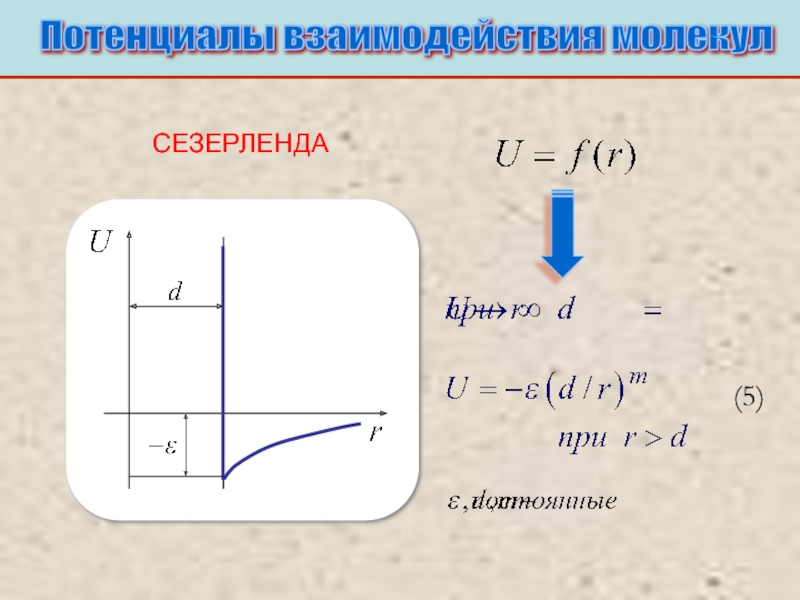
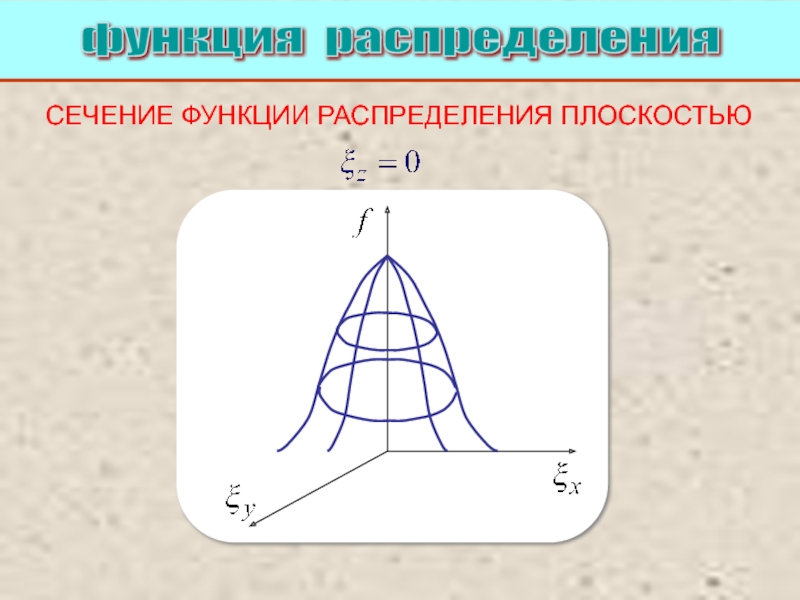
1. Физика конденсаторного состояния
2. ЛитератураФизика конденсированногосостоянияКоган М.Н. Динамика разреженного газа. М.:
3. жидкие кристаллыквантовые жидкостиФизика конденсированногосостояния
4. Физика конденсированного состояния (ФКС)Занимается фундаментальным изучением различных
5. Лауреаты Нобелевской премиив области физики низких температур
6. Физика конденсированного состоянияКонденсированная среда – система частиц, сильно взаимодействующих друг с другом.
7. Состояния веществаФизика конденсированногосостояния
8. Слайд 8
9. Слайд 9
10. микроскопическая теория процессов встатистически неравновесных системах
11. Основныепонятия иопределения
12. физическая кинетика
13. (1)
14. (2)Максвелловские молекулы s = 5(2a)
15. (3)
16. (4)
17. (5)
18. Слайд 18
19. Слайд 19
20. Слайд 20
21. СЕЧЕНИЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПЛОСКОСТЯМИ
22. Моменты функции распределения
23. Моменты функции распределенияПРИМЕРЫ МОМЕНТОВ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
24. ожидаемое число молекул в элементе объема физического
25. Моменты функции распределенияПРИМЕРЫ МОМЕНТОВ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
26. Моменты функции распределения
27. Слайд 27
28. Слайд 28
29. Слайд 29
30. ТРАЕКТОРИЯ ДВИЖЕНИЯ МОЛЕКУЛЫ
31. РАССМОТРЕНИЕ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ В ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ
32. Слайд 32
33. Для сумматорных инвариантов:Инварианты столкновений:Если ϕ - сумматорный инвариант, то
34. Слайд 34
35. Слайд 35
36. МОДЕЛЬНЫЕ УРАВНЕНИЯУравнение Бхатнагара, Гросса, Крукаν — постоянный
37. Слайд 37
38. Принятие аппроксимации функции распределения
39. Слайд 39
40. Слайд 40
41. Слайд 41
42. Слайд 42
43. Слайд 43
44. Слайд 44
45. Слайд 45
46. Слайд 46
47. Слайд 47
48. Слайд 48
49. Слайд 49
50. Слайд 50
51. Соотношение неопределенностей Гейзенберга:Неопределенность (флуктуации) энергии атома:
52. Слайд 52
53. Слайд 53
54. Слайд 54
55. Слайд 55
56. Слайд 56
57. Слайд 57
58. Слайд 58
59. Слайд 59
60. Слайд 60
61. Слайд 61
62. Слайд 62
63. Слайд 63
64. Слайд 64
65. Слайд 65
66. Слайд 66
67. Слайд 67
68. Слайд 68
69. Слайд 69
70. Слайд 70
71. Слайд 71
72. Слайд 72
73. Слайд 73
74. Слайд 74
75. Слайд 75
76. Слайд 76
77. Слайд 77
78. Слайд 78
79. Слайд 79
80. Слайд 80
81. Слайд 81
82. Слайд 82
83. Слайд 83
84. Слайд 84
85. Слайд 85
86. Слайд 86
87. Слайд 87
88. Слайд 88
89. Слайд 89
90. Слайд 90
91. Слайд 91
92. Слайд 92
93. Слайд 93
94. Слайд 94
95. Слайд 95
96. Слайд 96
97. Слайд 97
98. Скачать презентанцию

ЛитератураФизика конденсированногосостоянияКоган М.Н. Динамика разреженного газа. М.: Наука, 1967.Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. Сер. Теоретическая физика. Т.10. М.: Наука, 1979 Аристов В. В. , Черемисин Ф.Г. Прямое численное решение кинетического

Главная
Разное
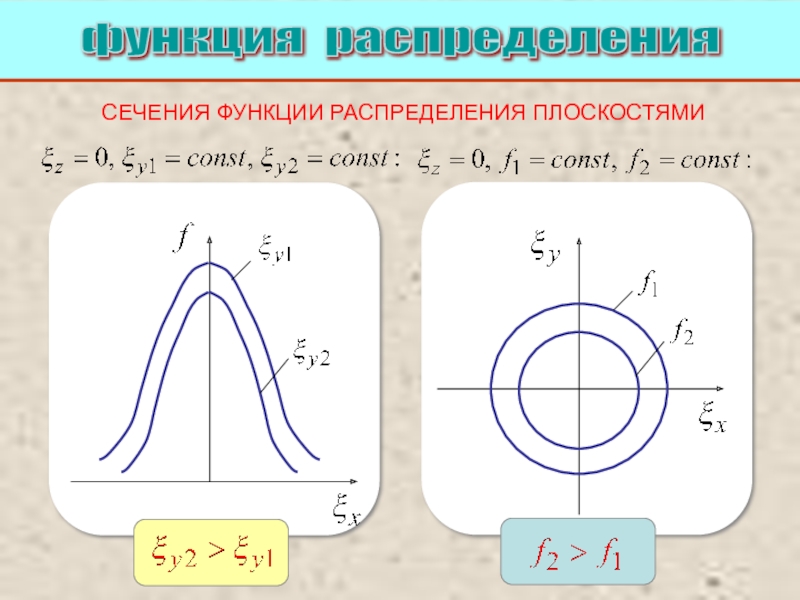
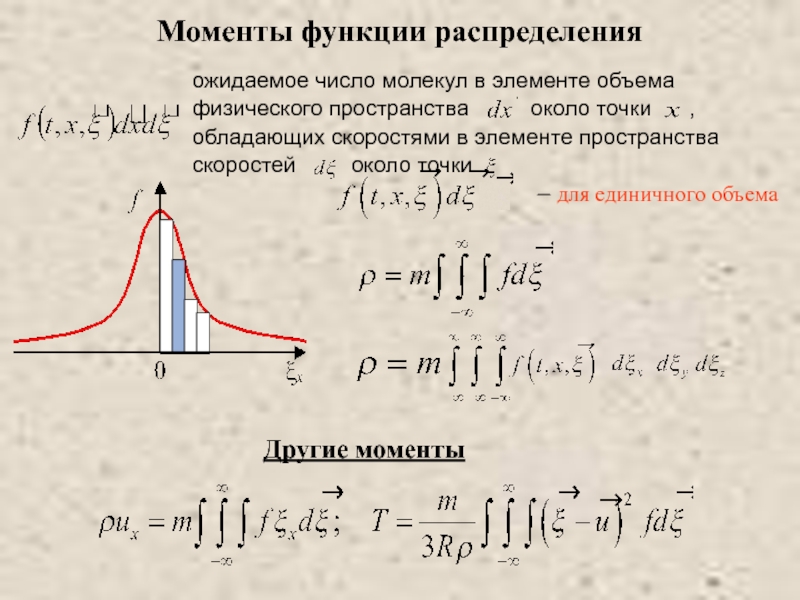
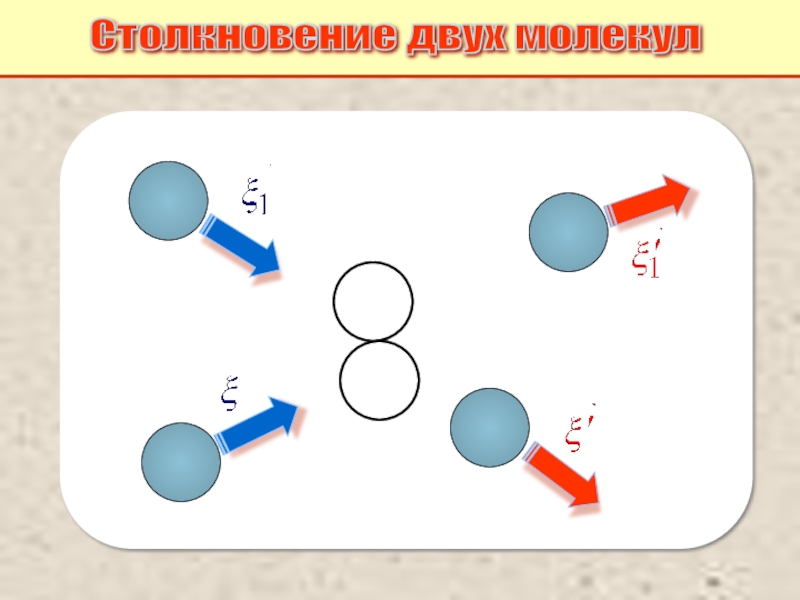
Физика конденсаторного состояния

Слайды и текст этой презентации

Слайд 1

Литература
Физика конденсированного
состояния
Крюков А.П. Элементы физической кинетики: учебное пособие. М.:

МЭИ, 1995.
Крюков А.П. Элементы гидродинамики и теплопереноса в гелии II:

учебное пособие. М.: МЭИ, 2004.
Дмитриев А.С. Основы криофизики конденсированных систем: учебное пособие. М.: МЭИ, 2006.

Основная

ЛитератураФизика конденсированногосостояния Крюков А.П. Элементы физической кинетики: учебное пособие. М.: МЭИ, 1995.Крюков А.П. Элементы гидродинамики и теплопереноса

Слайд 2

Литература
Физика конденсированного
состояния
Коган М.Н. Динамика разреженного газа. М.: Наука, 1967.
Лифшиц Е.М.,

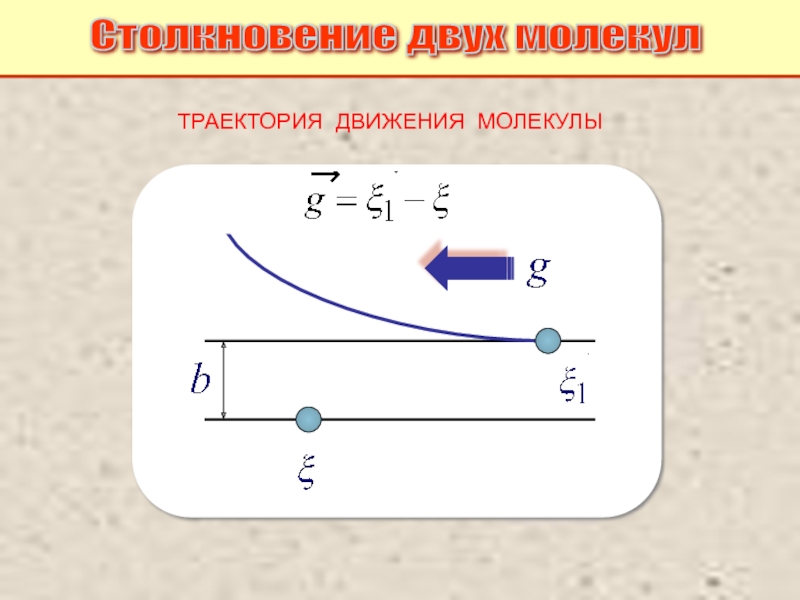
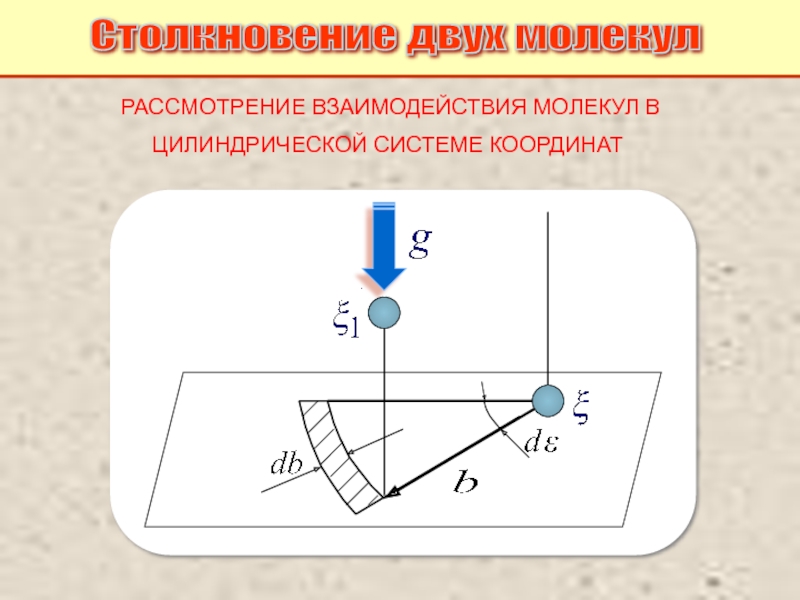
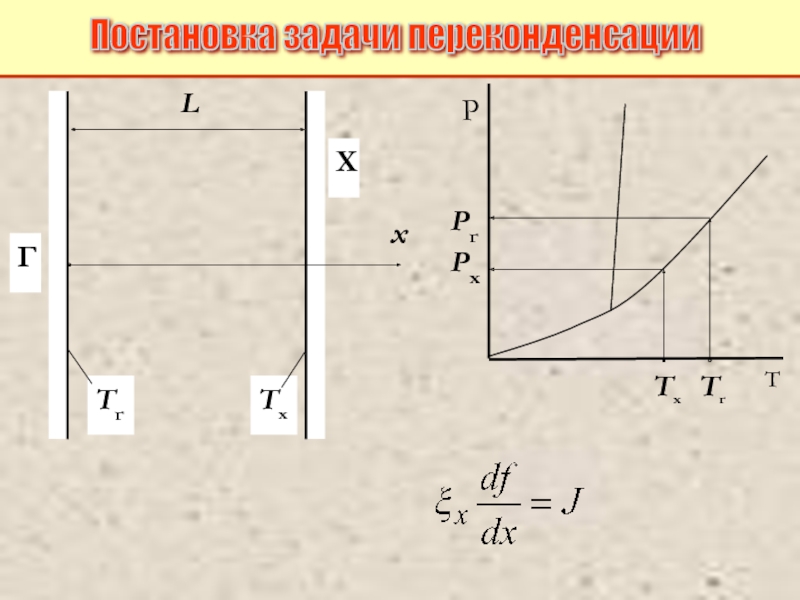
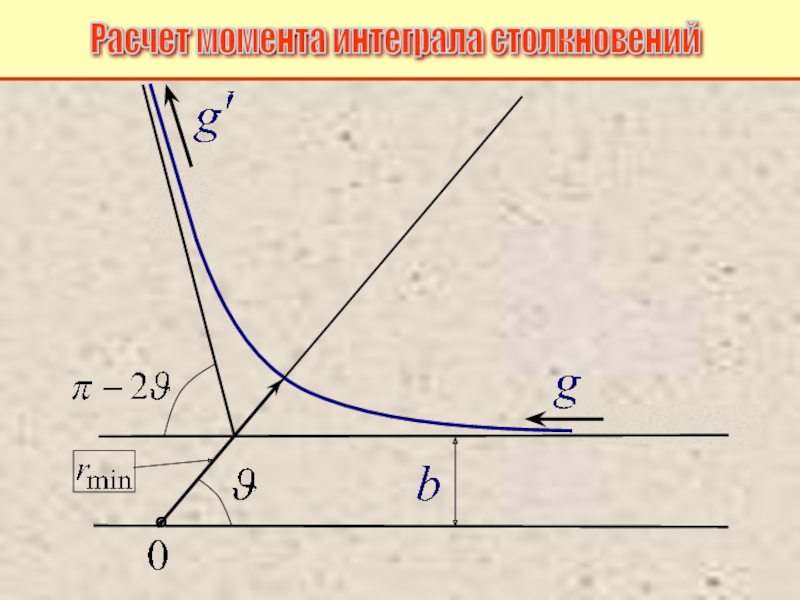
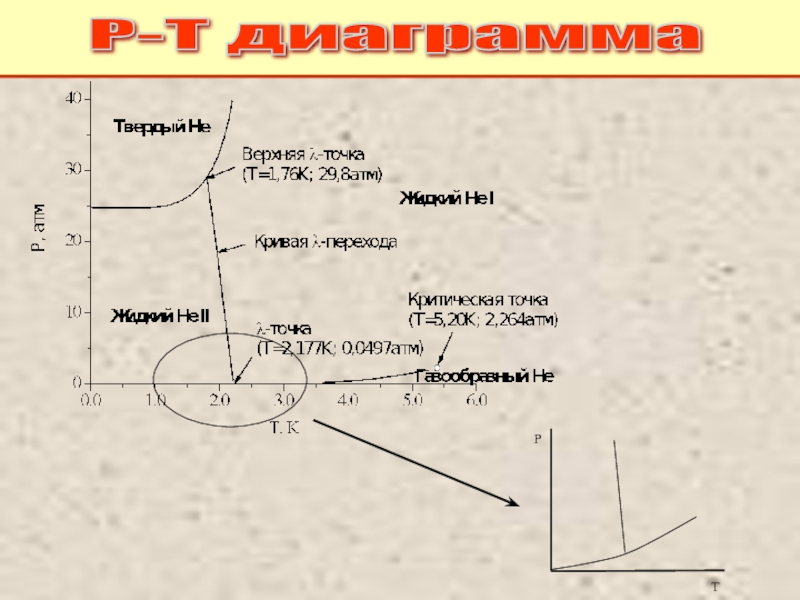
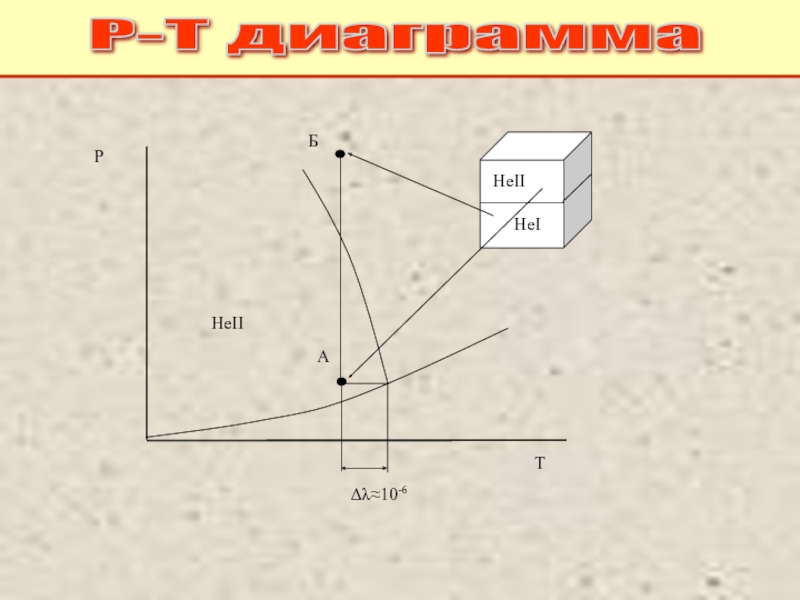
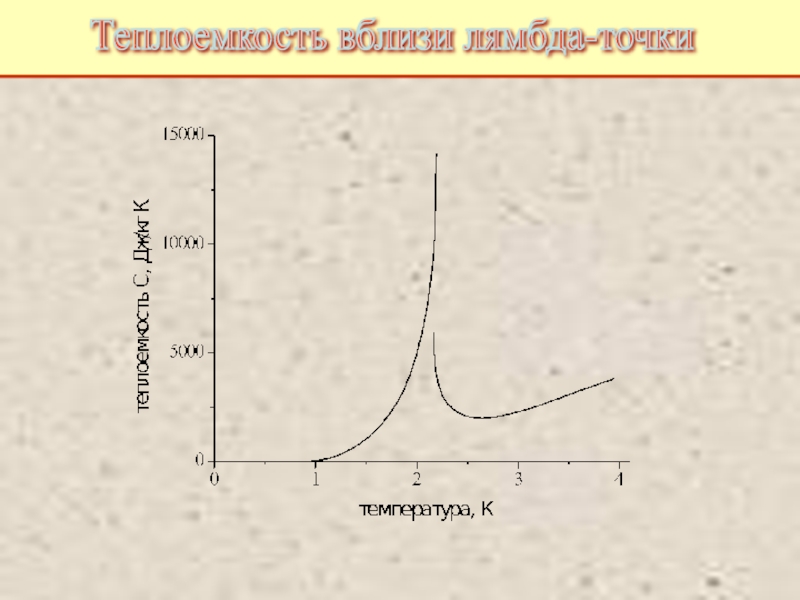
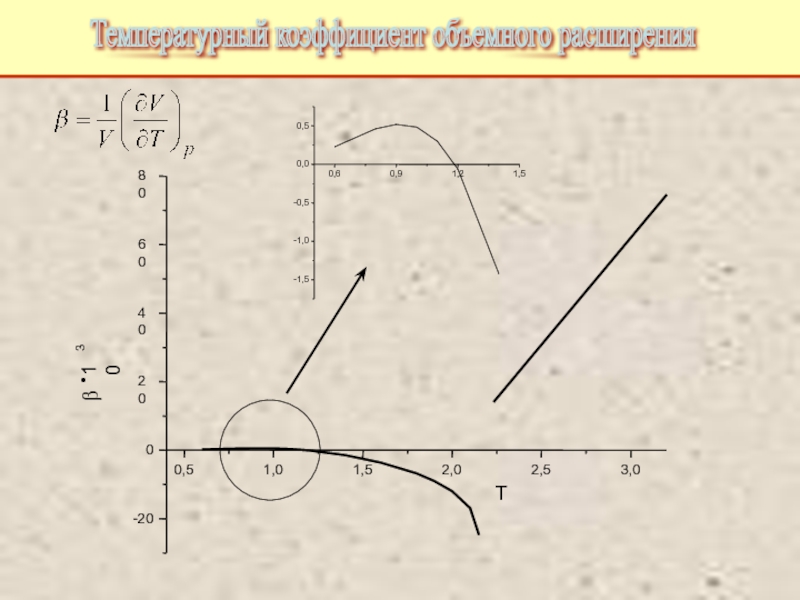
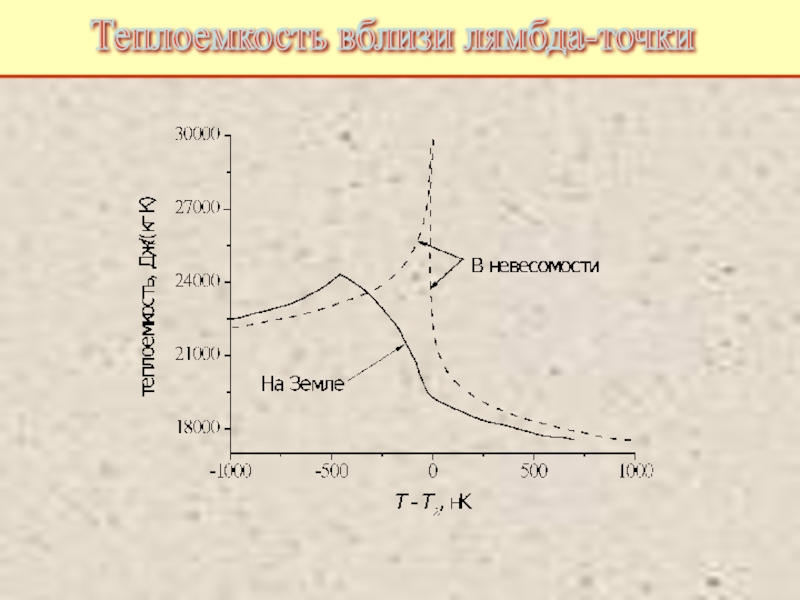
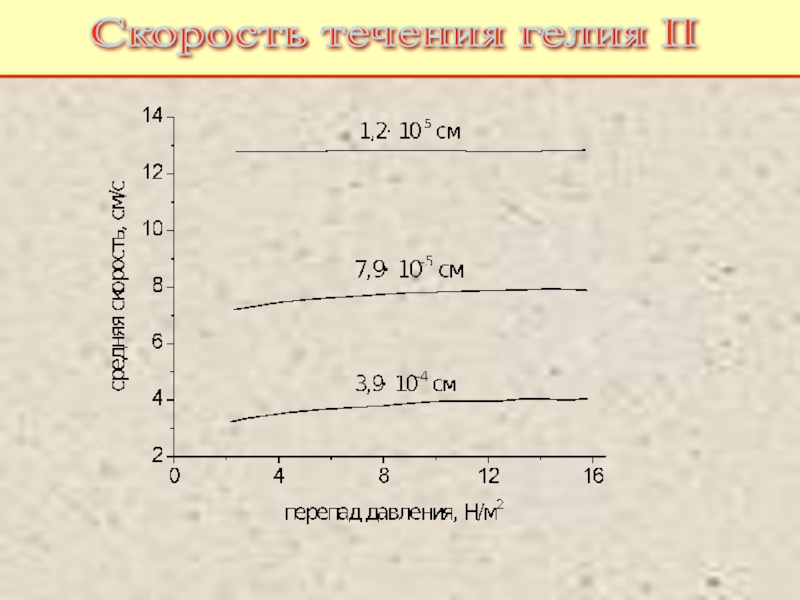
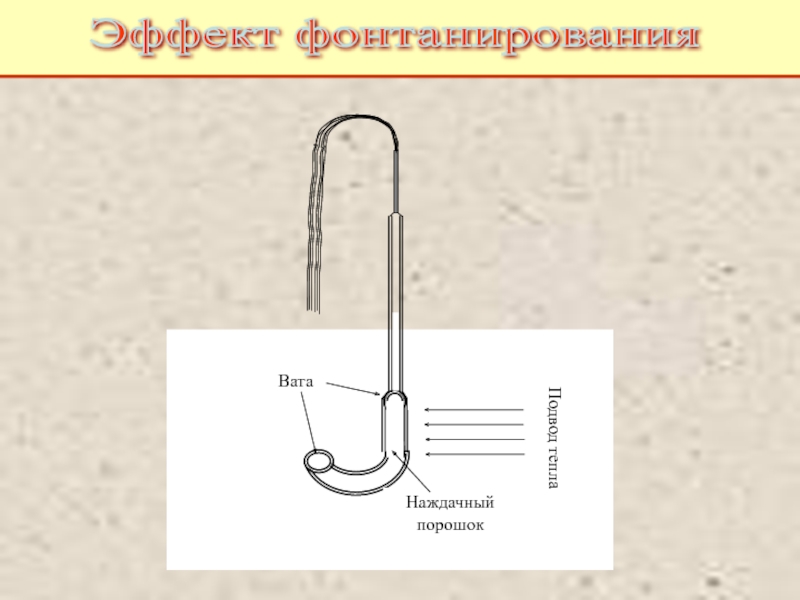
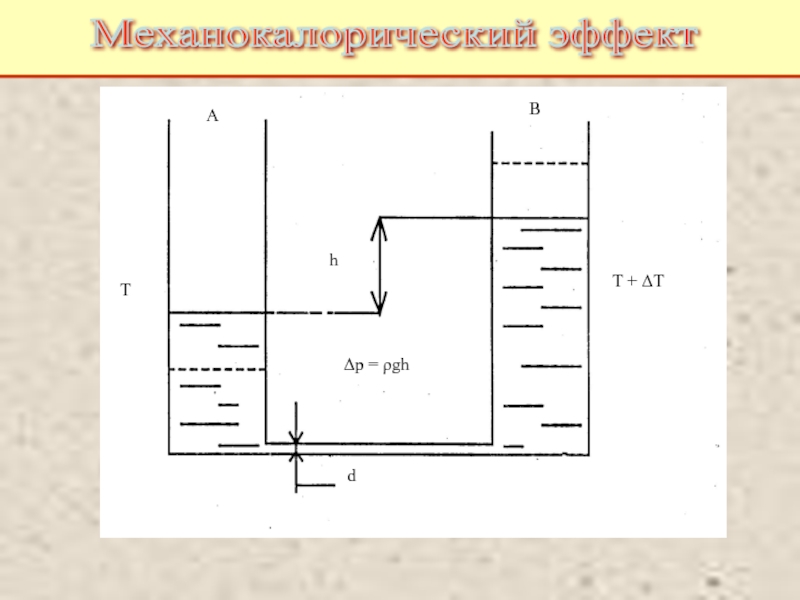
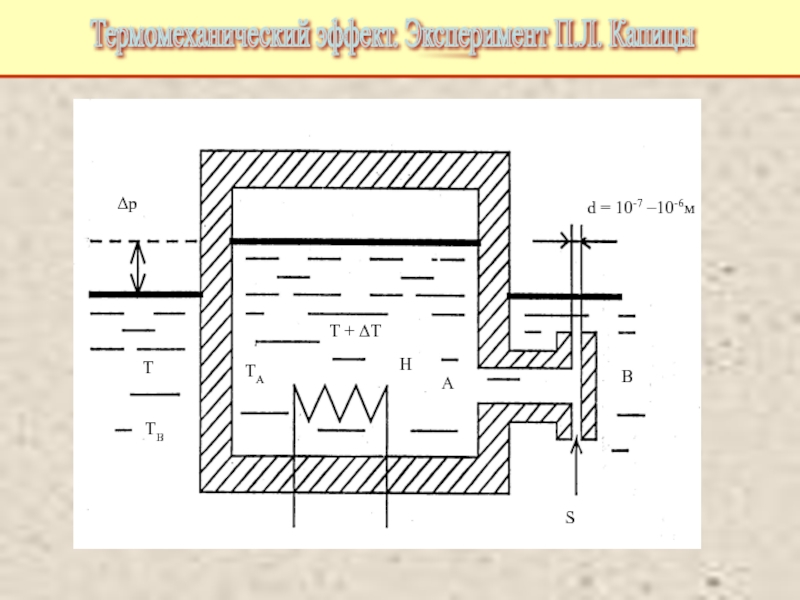
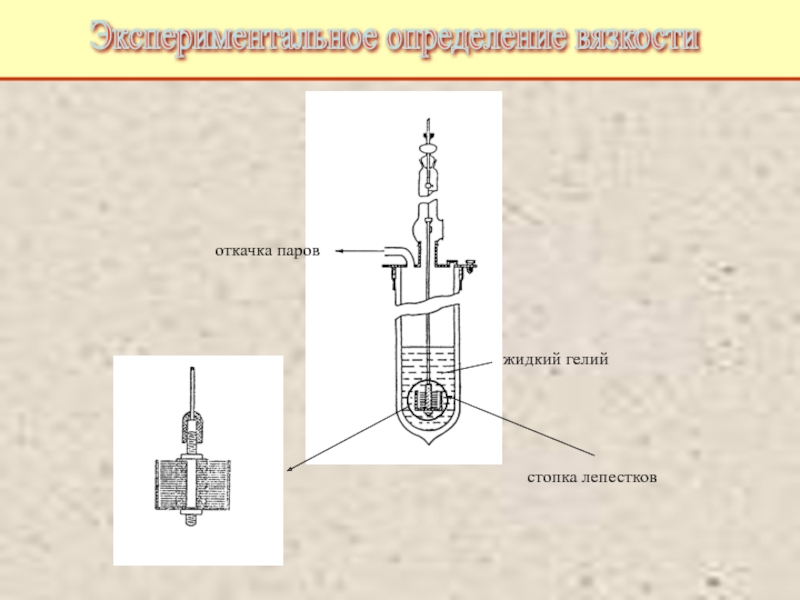
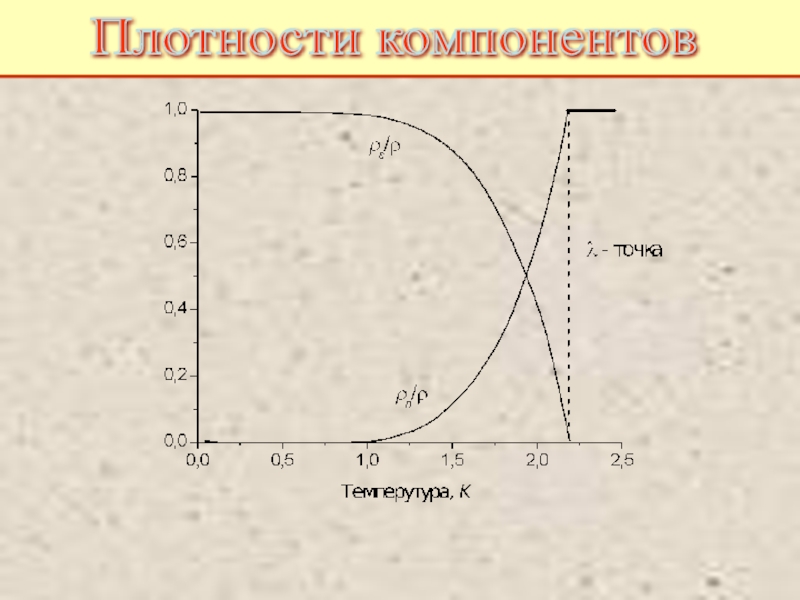
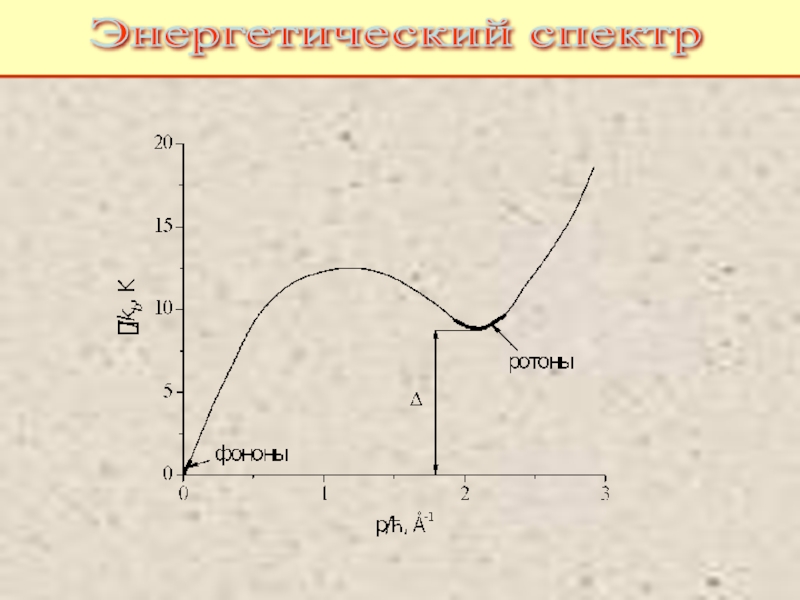
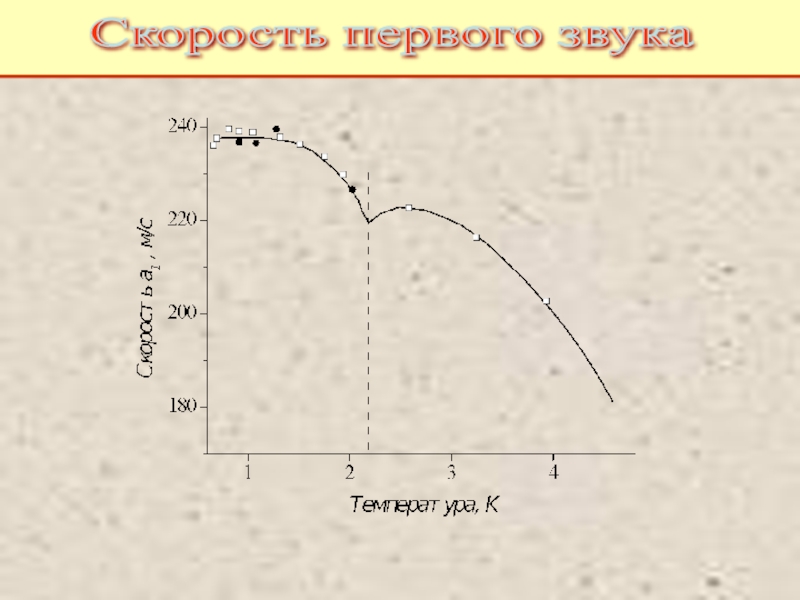
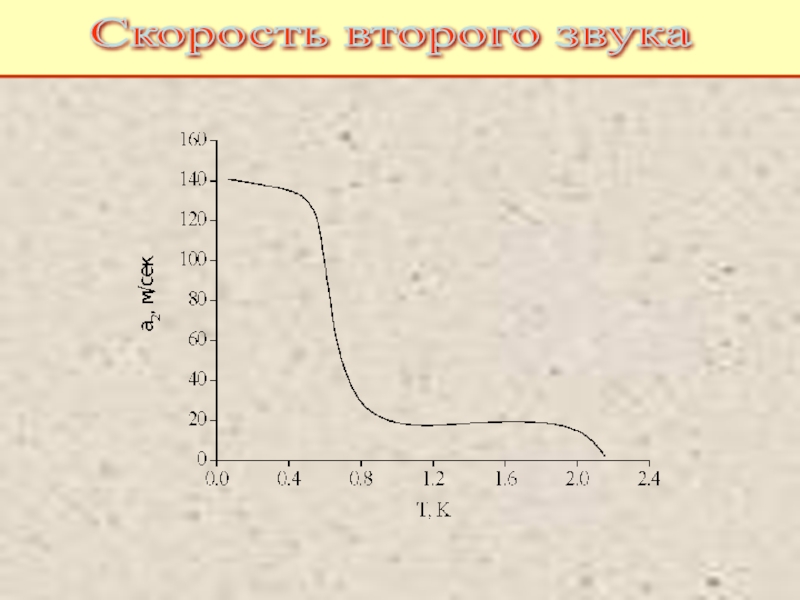
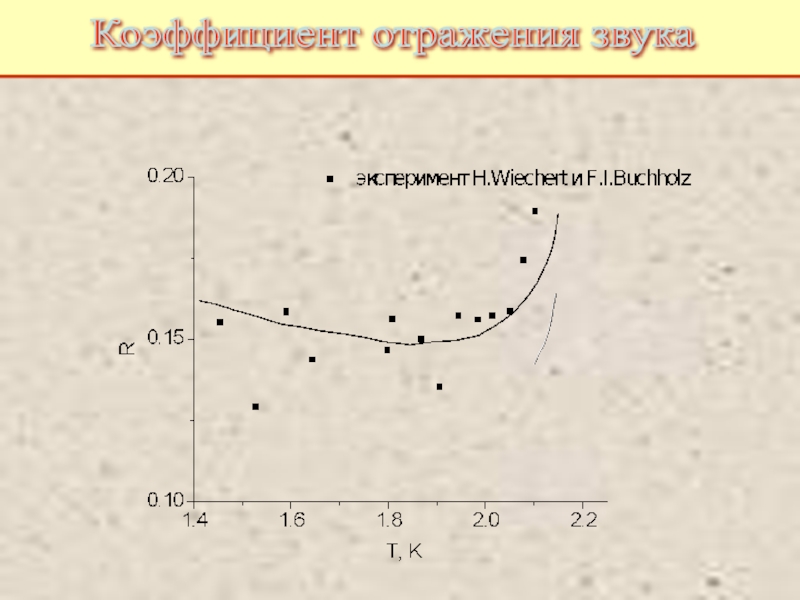
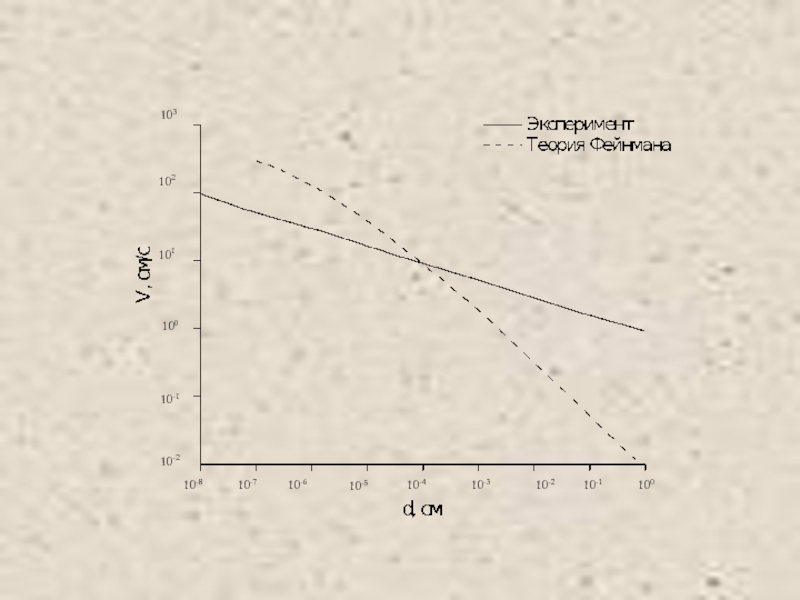
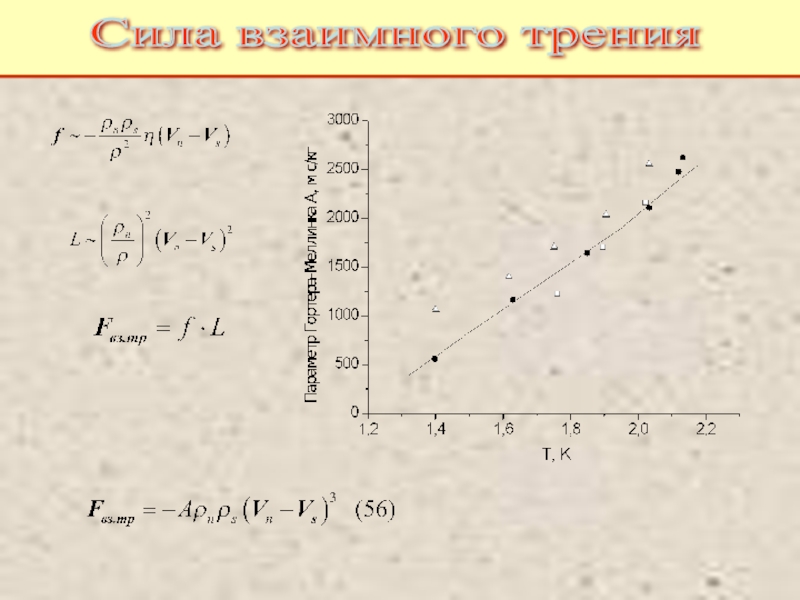
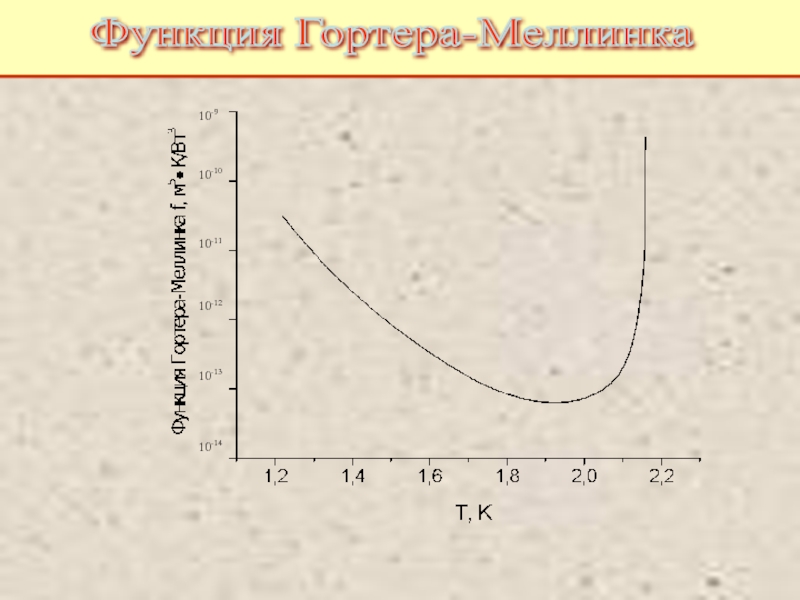
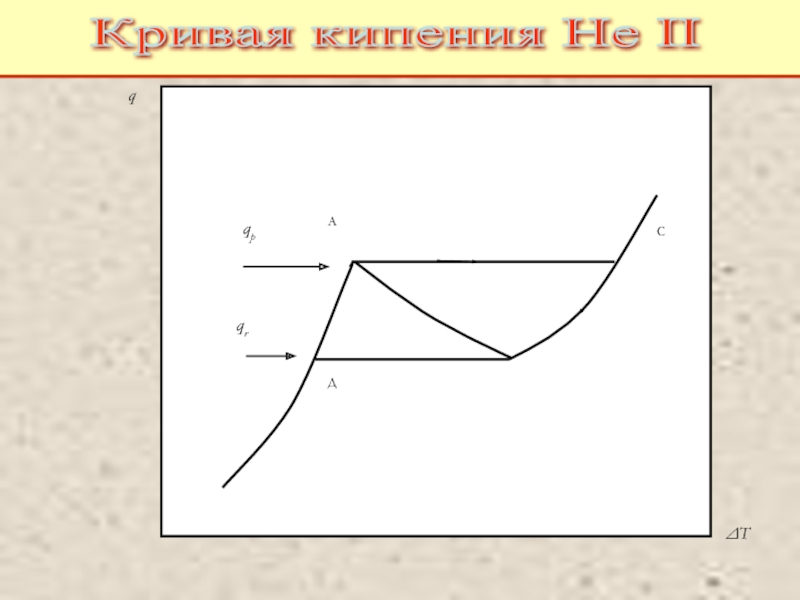
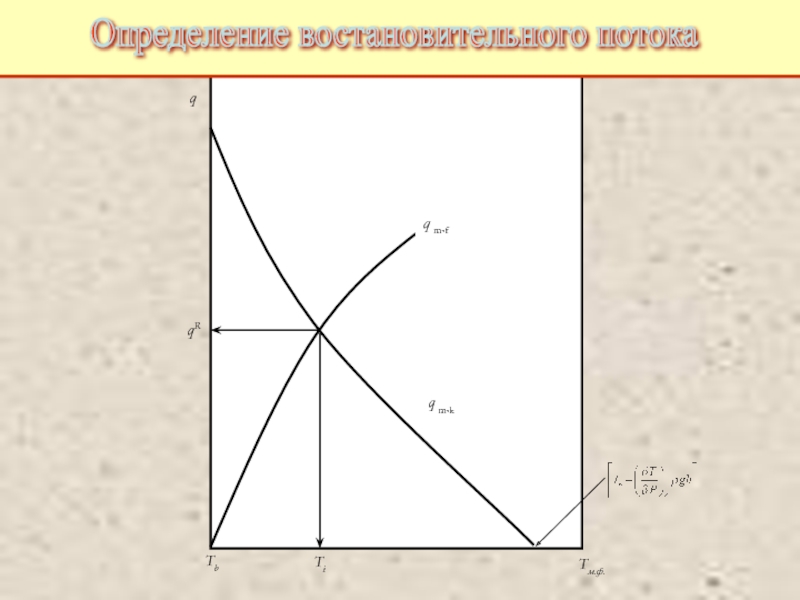
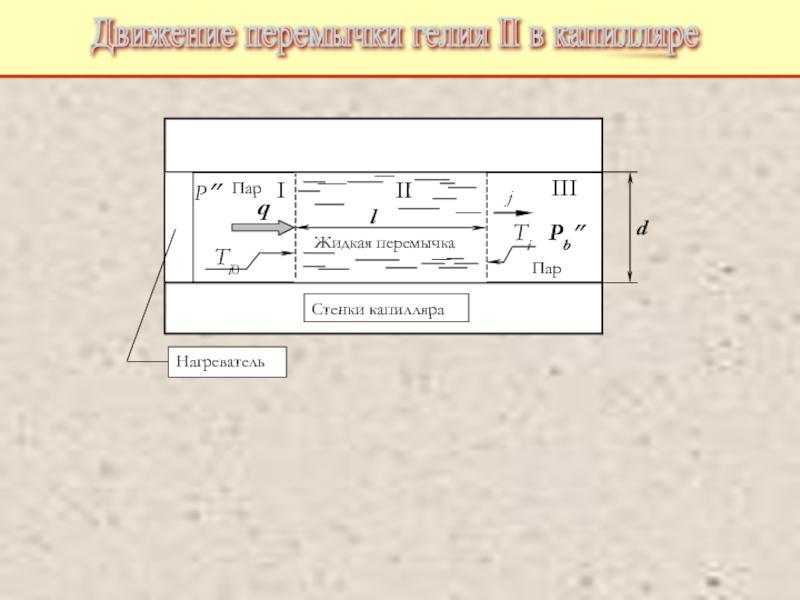
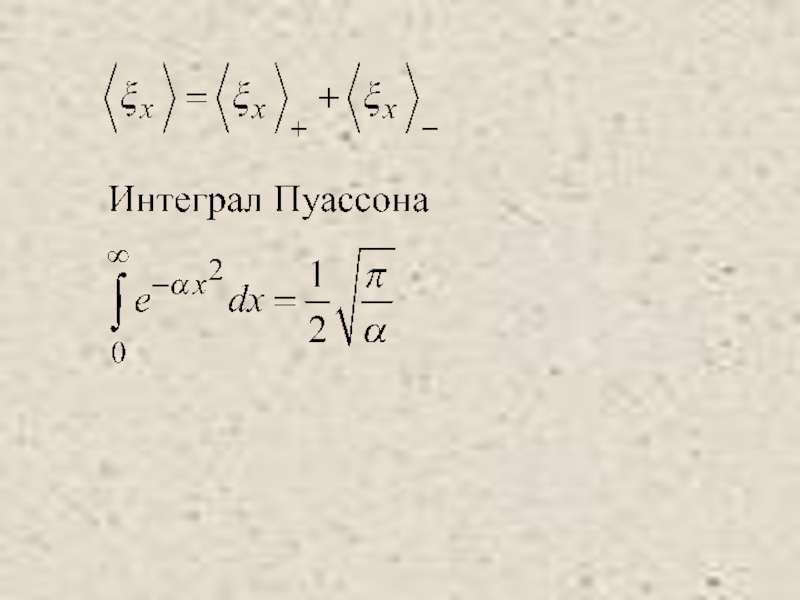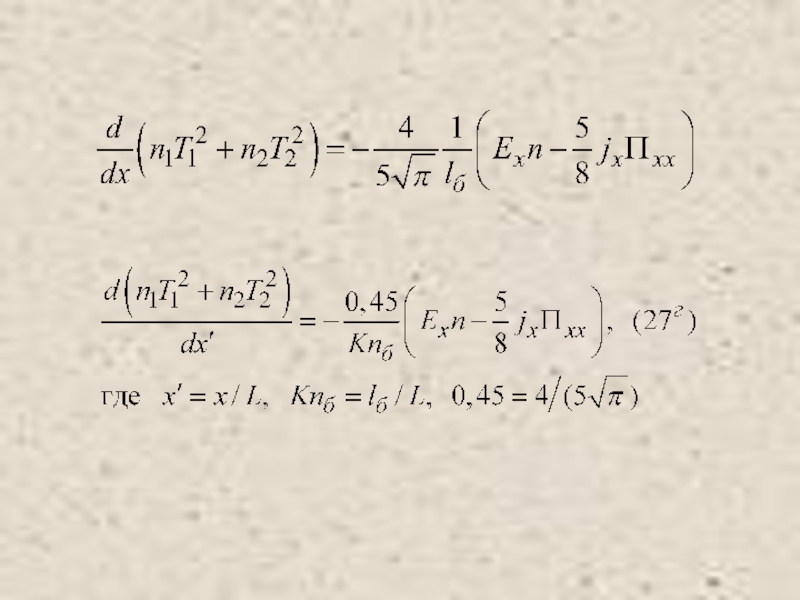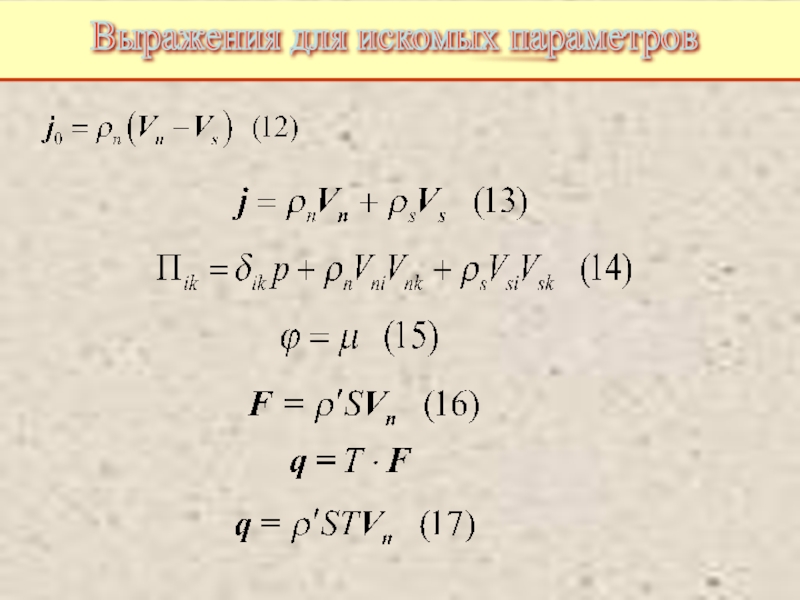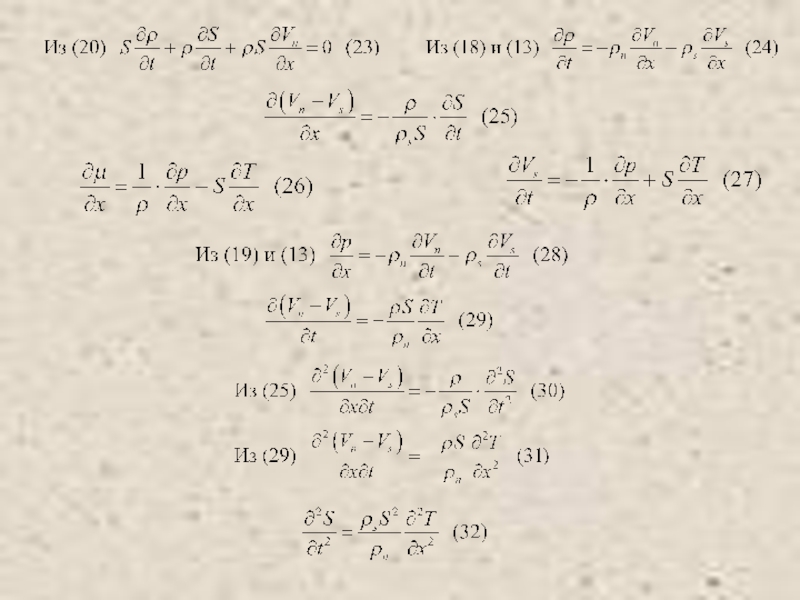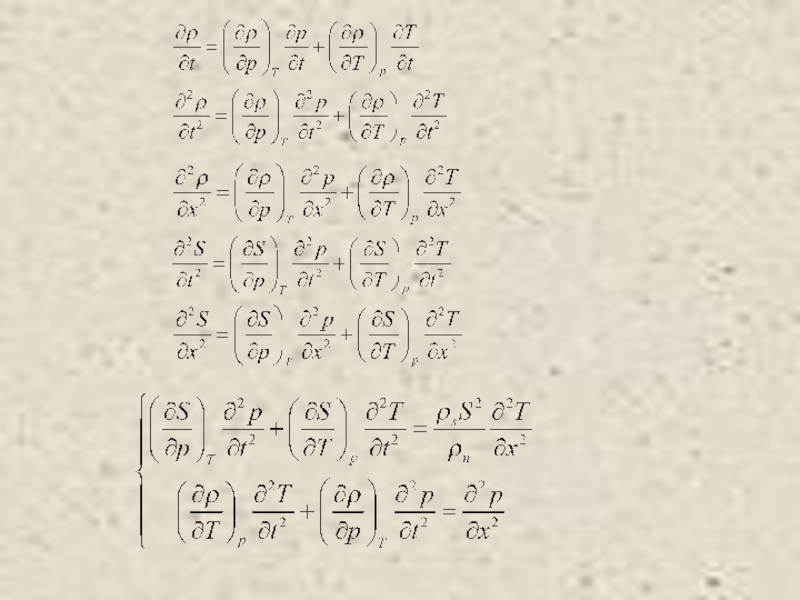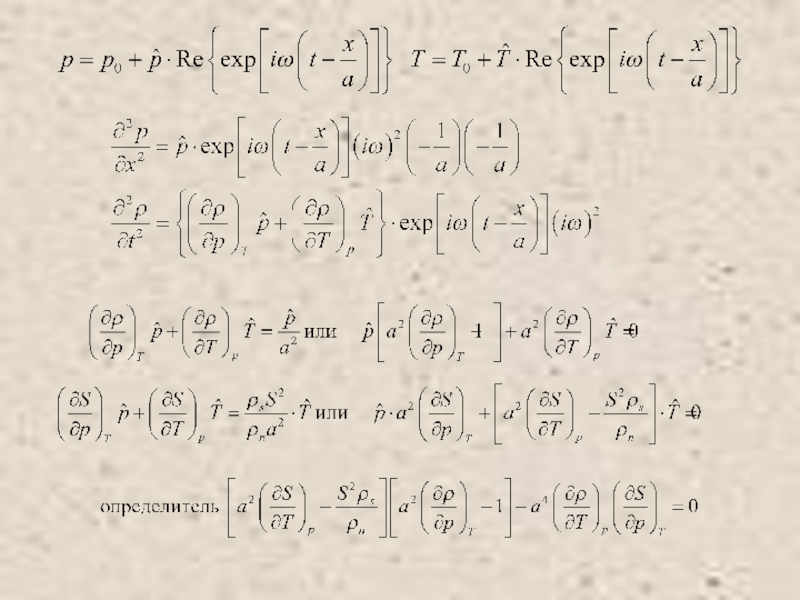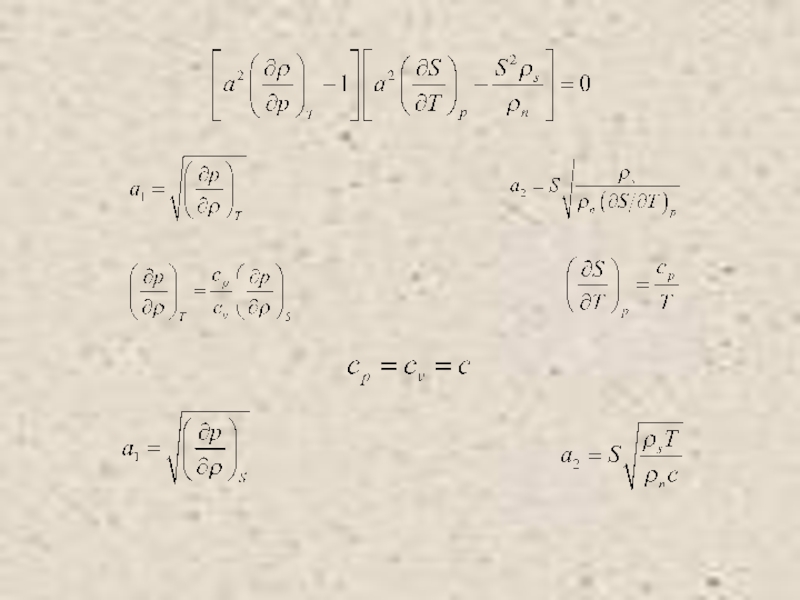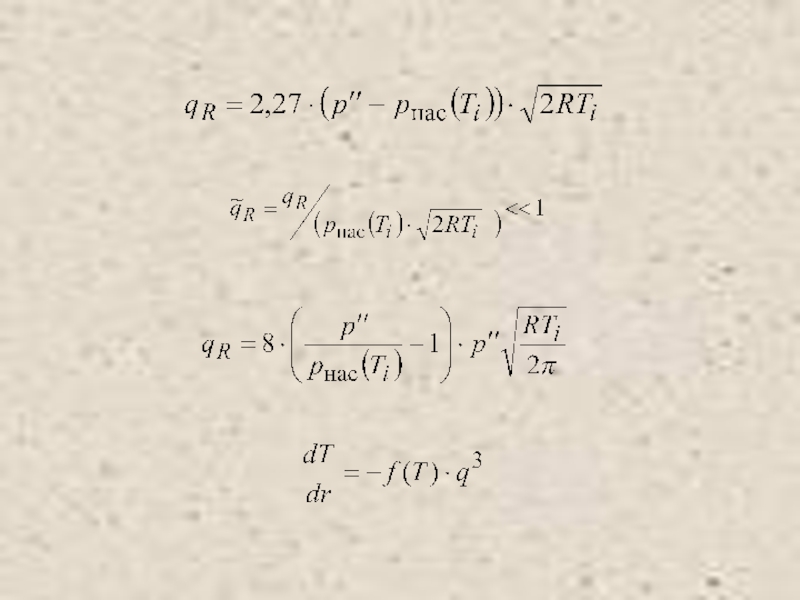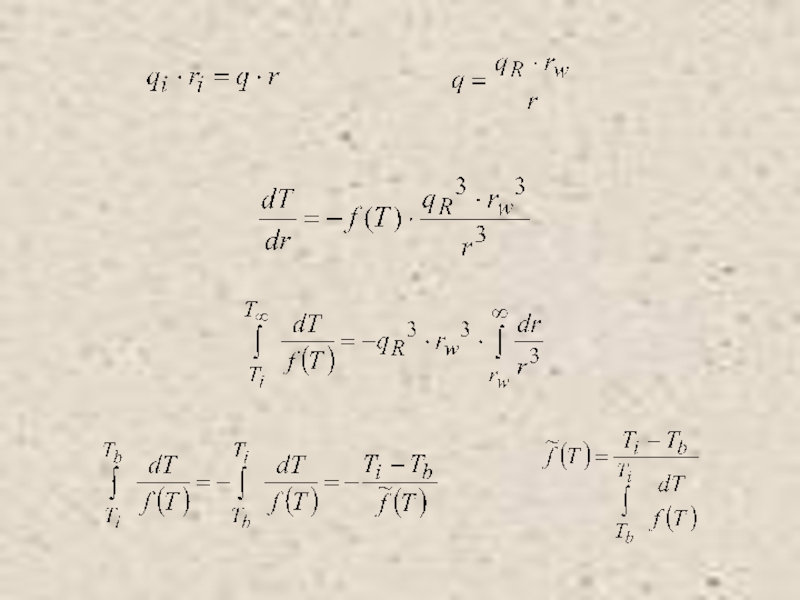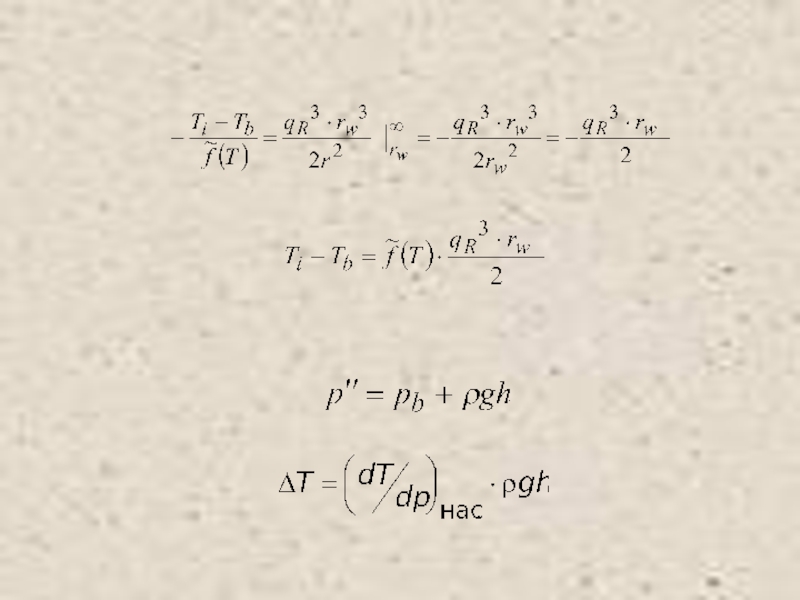Питаевский Л.П. Физическая кинетика. Сер. Теоретическая физика. Т.10. М.: Наука,

1979
Аристов В. В. , Черемисин Ф.Г. Прямое численное решение кинетического уравнения Больцмана. М.: ВЦ РАН, 1992.
Крюков А.П., Левашов В.Ю., Шишкова И.Н., Ястребов А.К. Численное решение кинетического уравнения Больцмана в инженерной практике: учебное пособие. М.: МЭИ, 2005.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. Сер. Теоретическая физика. Т.6. М.: Наука, 1988 (глава XVI, стр.706-730).
Халатников И.М. Теория сверхтекучести. М.: Наука, 1971.
Паттерман С. Гидродинамика сверхтекучей жидкости. М.: Мир, 1978.
Киттель Ч. Введение в физику твердого тела. М.: Наука, 1978.
Займан Дж. Принципы теории твердого тела. М.: Мир, 1974.

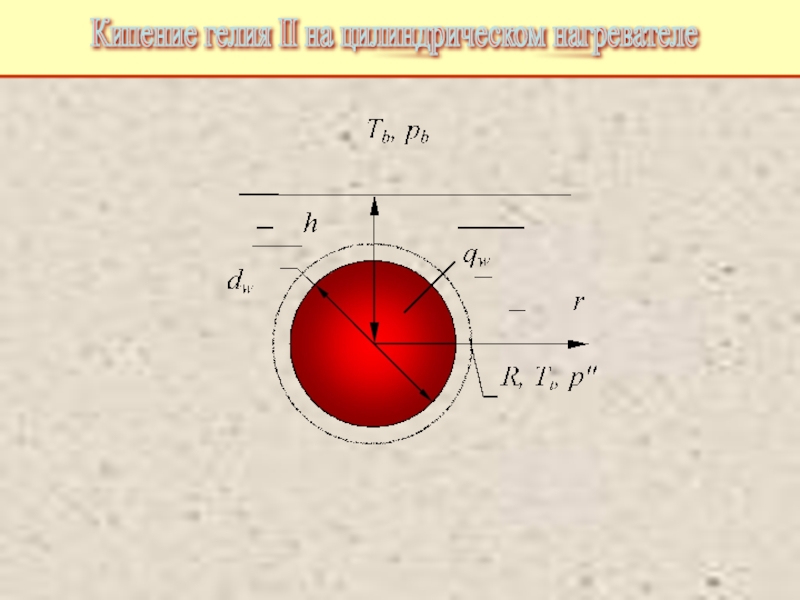
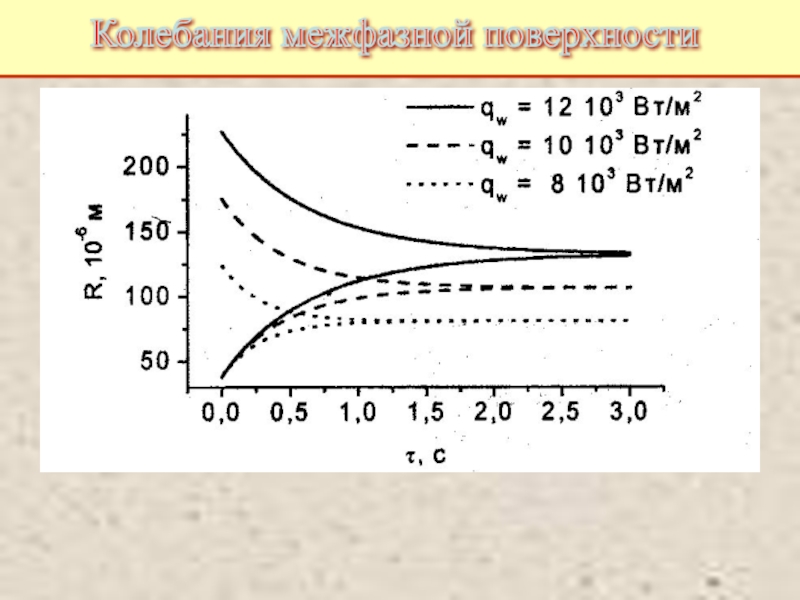
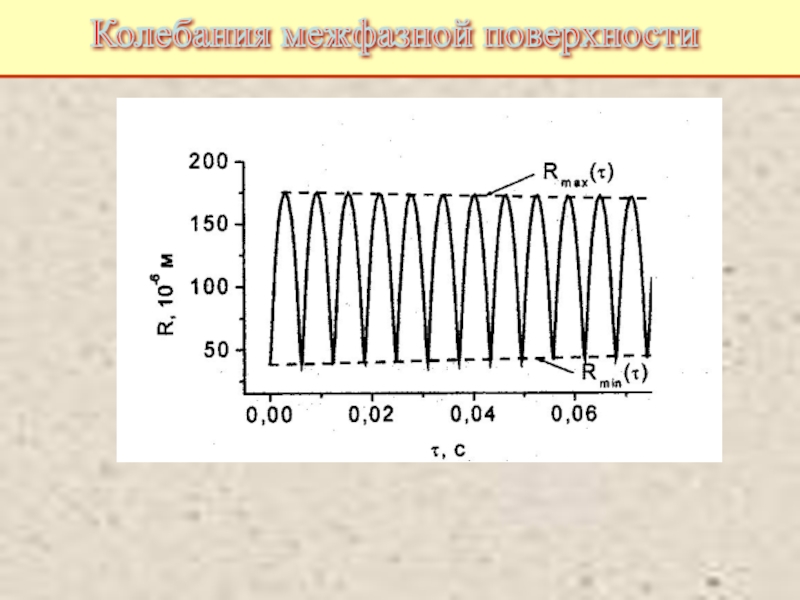
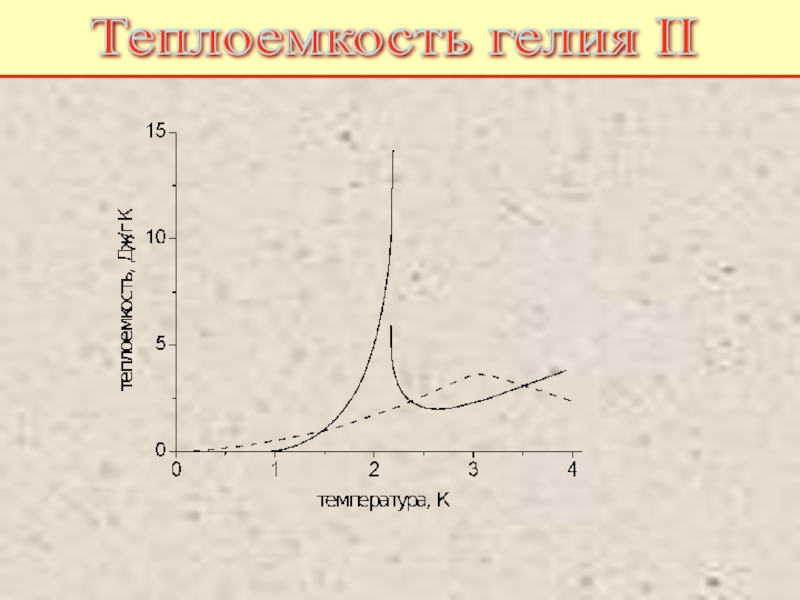
Дополнительная