Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция Суперпозиция Способы задания МНК
Содержание
- 1. Функция Суперпозиция Способы задания МНК
- 2. ФункцияПусть f: X→Y – функция. D(f) область определения функции E(f) область значений функции f.
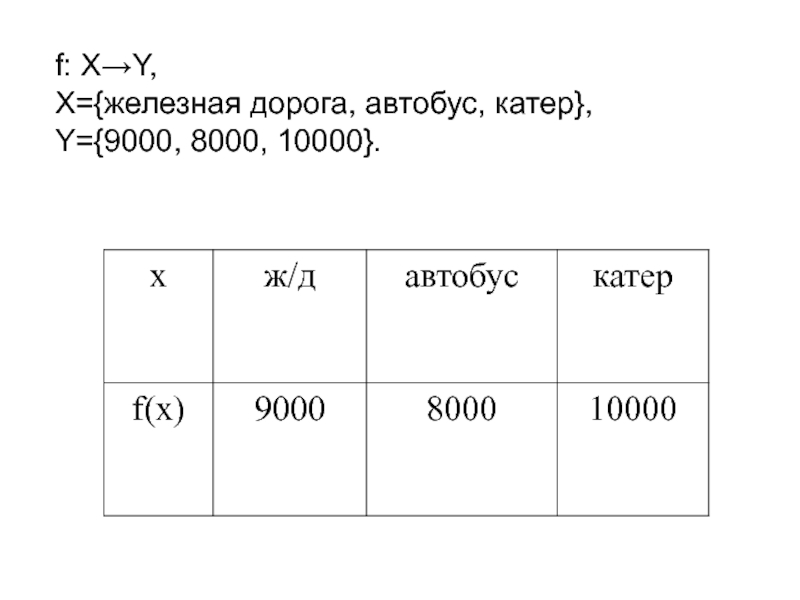
- 3. f: X→Y,Х={железная дорога, автобус, катер}, Y={9000, 8000, 10000}.
- 4. Х:={1, 2, 3}
- 5. ФормулаЕсли f=(X, Y, Qf), тоQf={(x, y)∈X×Y | y=f(x)}={(x, f(x))∈X×Y}
- 6. Композиция функцийf: X→Y и g: Y→Z. Функция h: X→Z является
- 7. Суперпозиция Функция, полученная из f1,…, fn некоторой подстановкой
- 8. f2(x)=x2,.f3(x)=1+x, .f4(x)=x1/2, , f(x)=f4(f3(f2(f1(x))))=f4f3f2f1(x),
- 9. f(х)=|х|
- 10. f: [–1,1]→[0,1], Qf ={(x, y)∈R2 | x2+y2=1}
- 11. Скачать презентанцию
ФункцияПусть f: X→Y – функция. D(f) область определения функции E(f) область значений функции f.
Слайды и текст этой презентации
Слайд 6Композиция функций
f: X→Y и g: Y→Z.
Функция h: X→Z является композицией функций f
и g
h=gf, если для любого x∈X h(x)=g(f(x)).
Часто говорят,
что функция h получена подстановкой f в g.
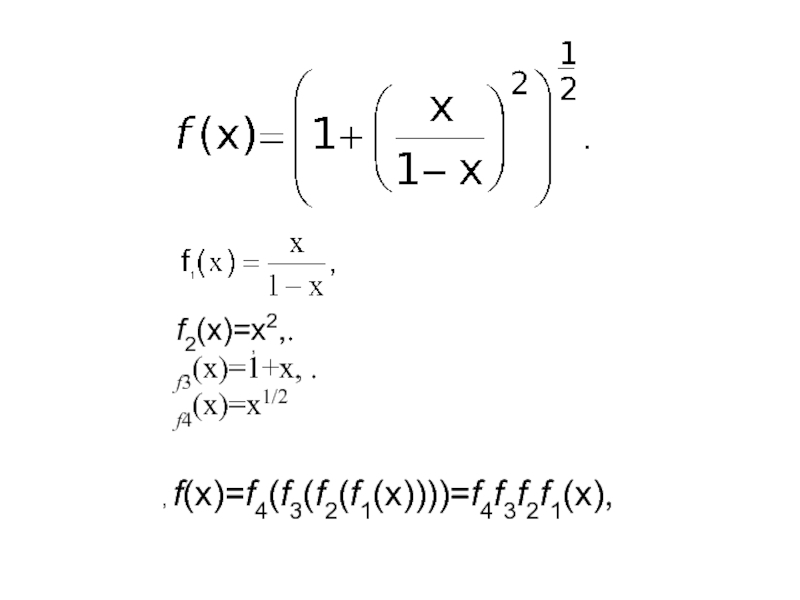
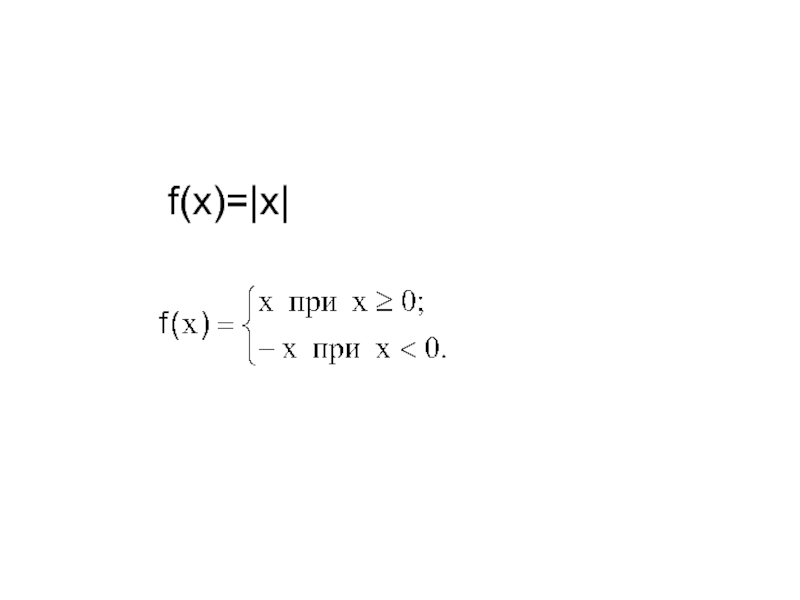
Слайд 7Суперпозиция
Функция, полученная из f1,…, fn некоторой подстановкой их друг в
друга и переименованием аргументов, называется суперпозицией f1,…, fn.
Выражение, описывающее эту
суперпозицию и содержащее функциональные знаки и символы аргументов, называется формулой.
![f: [–1,1]→[0,1], Qf ={(x, y)∈R2 | x2+y2=1}](/img/thumbs/1657157380478dad155c4155ec0500e3-800x.jpg "Функция Суперпозиция Способы задания МНК f: [–1,1]→[0,1], Qf ={(x, y)∈R2 | x2+y2=1}")
