TheSlide.ru

Функции, пределы, непрерывности

Содержание

1. Функции, пределы, непрерывности
2. Основные вопросы:Понятие предела функции.Основные теоремы о пределах
3. Предел функцииПредел – одно из основных понятий
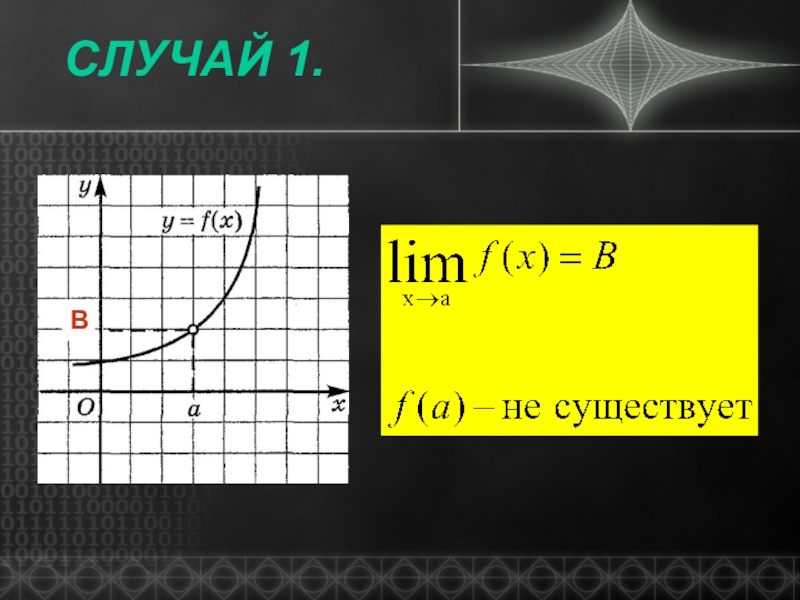
4. Случай 1.В
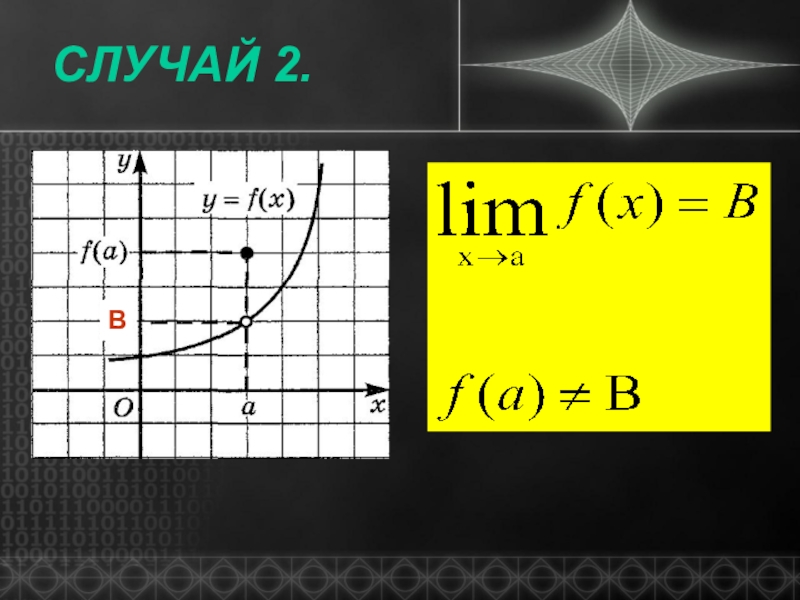
5. Случай 2.В
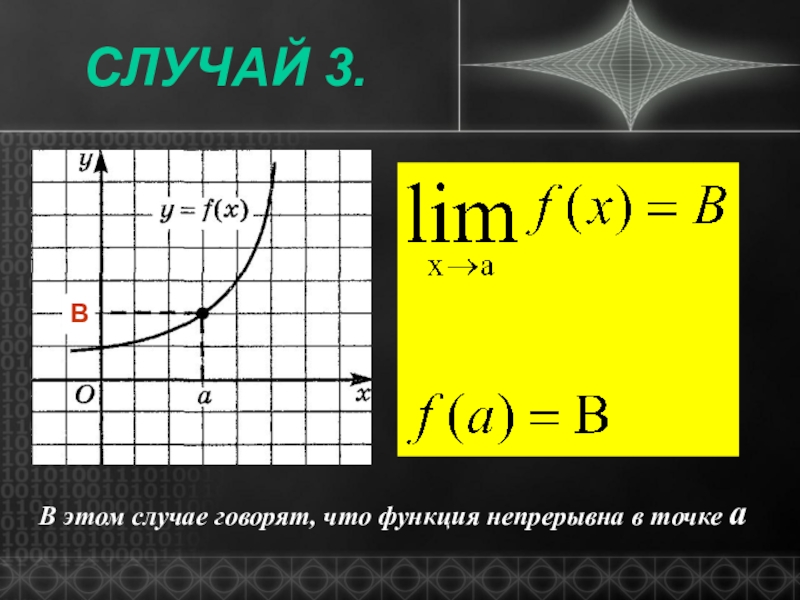
6. Случай 3.ВВ этом случае говорят, что функция непрерывна в точке а
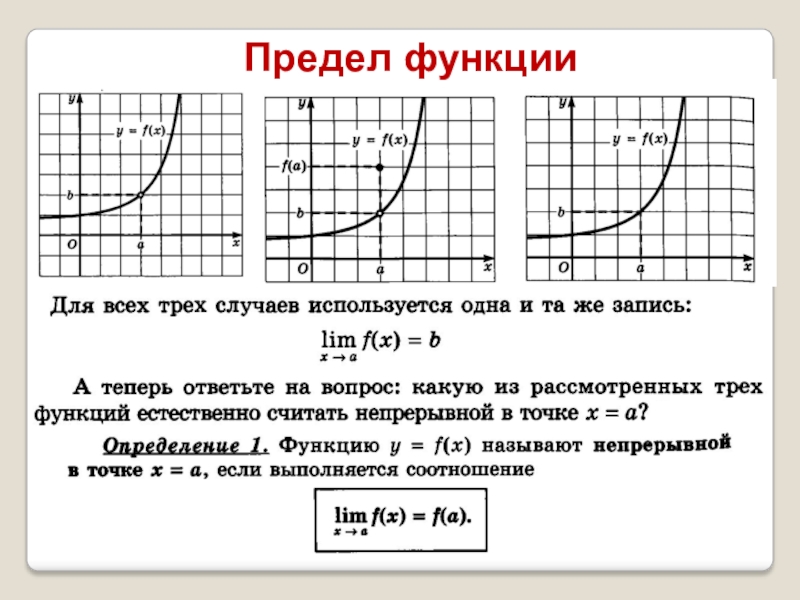
7. Предел функции
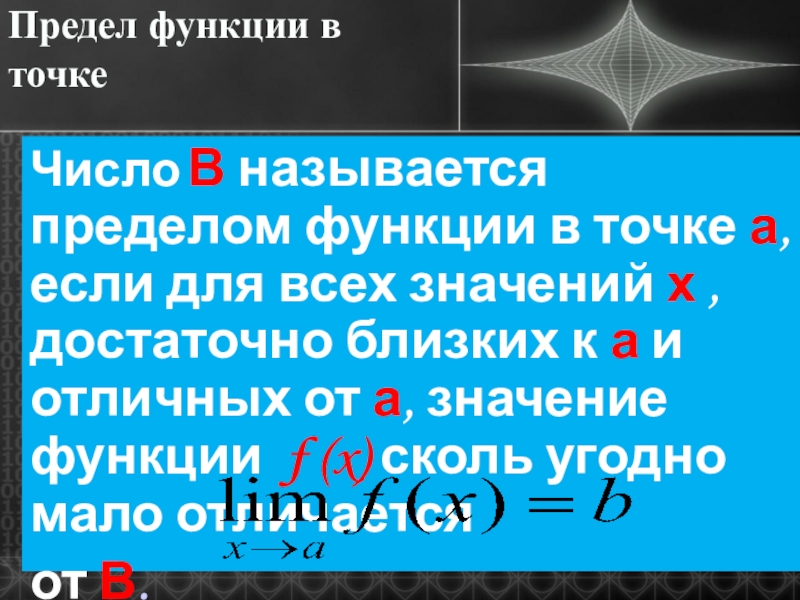
8. Предел функции в точкеЧисло В называется пределом
9. Теорема 1. Предел суммы (разности) 2-х функций равен сумме (разности) их пределов, если последние существуют:
10. Теорема 2. Предел константы равен самой этой константе.
11. Теорема 3. Предел произведения 2-х функций равен произведению их пределов, если последние существуют:
12. Теорема 4. Предел отношения 2-х функций равен
13. Теорема 5. Постоянный множитель можно выносить за знак предела
14. Теорема 6. Предел степени переменного равен той же степени предела основания:
15. Вычисление пределовВычисление предела:начинают с подстановки предельного значения
16. Вычислить пределы:
17. Примеры
18. Последовательности, пределы.
19. Вычисление пределовЧасто при подстановке предельного значения x0
20. Методы вычисления пределов на неопределенность Раскрыть соответствующую
21. В большинстве случаев, чтобы раскрыть неопределенность вида
22. Пример №1: Разложим числитель и знаменатель на множители:
23. Пример № 2:
24. Чтобы раскрыть неопределенность данного вида, зависящую от
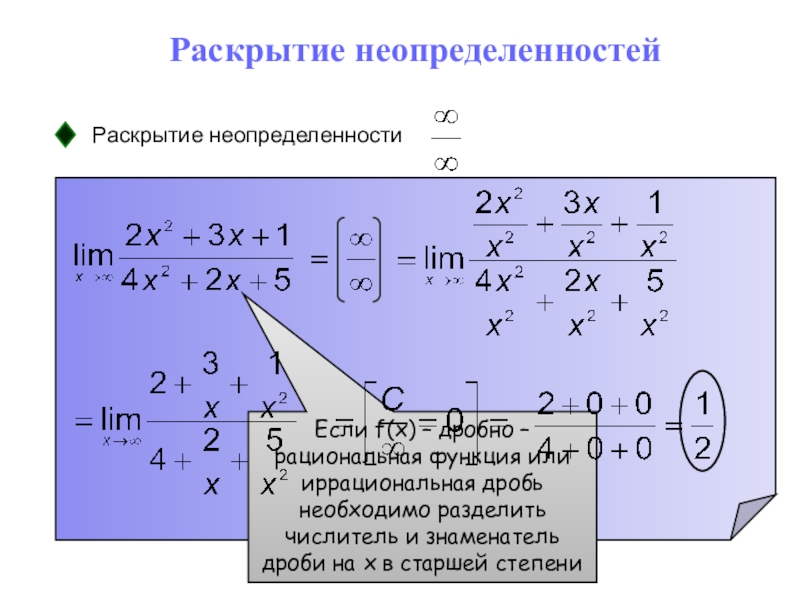
25. Раскрытие неопределенностейРаскрытие неопределенностиЕсли f(x) – дробно –
26. Слайд 26
27. Основные правила раскрытия неопределенностей вида В процессе вычисления пределов функций могут встретиться разные случаи:
28. Прямую подстановку использовать нельзя
29. Бывают неопределённости вида Чтобы раскрыть неопределенность вида
30. Раскрытие неопределенностейРаскрытие неопределенностиЕсли f(x) – дробно –
31. Замечание: если в числителе
32. Например:
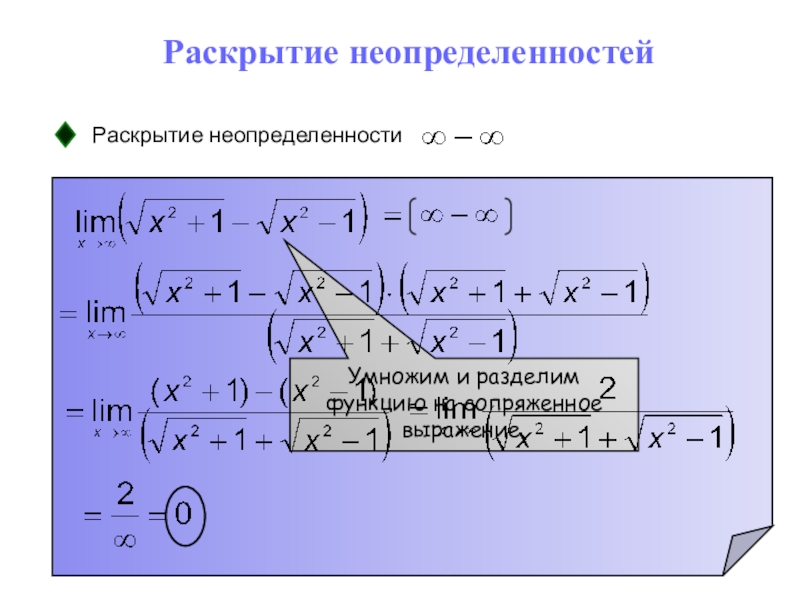
33. Раскрытие неопределенностейРаскрытие неопределенностиУмножим и разделим функцию на сопряженное выражение.
34. Упражнения:
35. Упражнения:
36. Упражнения:
37. Домашнее задание:Колесов В.В. Математика для медицинских колледжей:
38. Скачать презентанцию

Основные вопросы:Понятие предела функции.Основные теоремы о пределах функций (суммы, произведения и частного).Методы вычисления пределов на неопределенность( ).

Главная
Разное
Функции, пределы, непрерывности

Слайды и текст этой презентации

Слайд 1Функции, пределы, непрерывности.

Функции, пределы, непрерывности.

Слайд 2Основные вопросы:
Понятие предела функции.
Основные теоремы о пределах функций (суммы, произведения

и частного).
Методы вычисления пределов на неопределенность( ).

Основные вопросы:Понятие предела функции.Основные теоремы о пределах функций (суммы, произведения и частного).Методы вычисления пределов на неопределенность(

Слайд 3Предел функции
Предел – одно из основных понятий математического анализа. Понятие

предела использовалось еще Ньютоном во второй половине XVII века и

математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.

Различают – предел функции в точке и предел функции на бесконечности.

Предел функцииПредел – одно из основных понятий математического анализа. Понятие предела использовалось еще Ньютоном во второй половине

Слайд 4Случай 1.
В

Случай 1.В

Слайд 5Случай 2.
В

Случай 2.В

Слайд 6Случай 3.
В
В этом случае говорят, что функция непрерывна в точке

Случай 3.ВВ этом случае говорят, что функция непрерывна в точке а

Слайд 7Предел функции

Предел функции

Слайд 8Предел функции в точке
Число В называется пределом функции в точке

а, если для всех значений х , достаточно близких к

а и отличных от а, значение функции f (x) сколь угодно мало отличается
от В.

Предел функции в точкеЧисло В называется пределом функции в точке а, если для всех значений х ,

Слайд 9Теорема 1.

Предел суммы (разности) 2-х функций равен сумме (разности)

их пределов, если последние существуют:

Теорема 1. Предел суммы (разности) 2-х функций равен сумме (разности) их пределов, если последние существуют:

Слайд 10Теорема 2.

Предел константы равен самой этой константе.

Теорема 2. Предел константы равен самой этой константе.

Слайд 11Теорема 3.

Предел произведения 2-х функций равен произведению их пределов,

если последние существуют:

Теорема 3. Предел произведения 2-х функций равен произведению их пределов, если последние существуют:

Слайд 12Теорема 4.

Предел отношения 2-х функций равен отношению) их пределов,

если последние существуют и предел знаменателя отличен от 0:

Теорема 4. Предел отношения 2-х функций равен отношению) их пределов, если последние существуют и предел знаменателя отличен

Слайд 13Теорема 5.

Постоянный множитель можно выносить за знак предела

Теорема 5. Постоянный множитель можно выносить за знак предела

Слайд 14Теорема 6.

Предел степени переменного равен той же степени предела

основания:

Теорема 6. Предел степени переменного равен той же степени предела основания:

Слайд 15Вычисление пределов
Вычисление предела:
начинают с подстановки предельного значения x0 в функцию

f(x).
Если при этом получается конечное число, то предел равен этому

числу.

Если при подстановки предельного значения x0 в функцию f(x) получаются выражения вида:

то предел будет равен:

Вычисление пределовВычисление предела:начинают с подстановки предельного значения x0 в функцию f(x).Если при этом получается конечное число, то

Слайд 16Вычислить пределы:

Вычислить пределы:

Слайд 17Примеры

Примеры

Слайд 18Последовательности, пределы.

Последовательности, пределы.

Слайд 19Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x)

получаются выражения следующих видов:
Эти выражения называются неопределенности, а вычисление пределов

в этом случае называется раскрытие неопределенности.

Вычисление пределовЧасто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов:Эти выражения называются неопределенности,

Слайд 20Методы вычисления пределов на неопределенность
Раскрыть соответствующую неопределенность- это значит

найти предел (если он существует) соответствующего выражения, что, однако не

всегда просто.

Методы вычисления пределов на неопределенность Раскрыть соответствующую неопределенность- это значит найти предел (если он существует) соответствующего выражения,

Слайд 21В большинстве случаев, чтобы раскрыть неопределенность вида

, достаточно
числитель и знаменатель дроби разделить на

множители, и затем сократить на множитель, приводящий к неопределенности.

Правило № 1

В большинстве случаев, чтобы раскрыть неопределенность вида , достаточно числитель и знаменатель дроби

Слайд 22Пример №1:

Разложим числитель и знаменатель на множители:

Пример №1: Разложим числитель и знаменатель на множители:

Слайд 23Пример № 2:

Пример № 2:

Слайд 24Чтобы раскрыть неопределенность данного вида, зависящую от иррациональности, достаточно перевести

иррациональность (или иррациональности) из числителя в знаменатель или из знаменателя

в числитель и сократить на множитель, приводящий к неопределенности.

Правило № 2

Чтобы раскрыть неопределенность данного вида, зависящую от иррациональности, достаточно перевести иррациональность (или иррациональности) из числителя в знаменатель

Слайд 25Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция, необходимо

разложить на множители числитель и знаменатель дроби
Если f(x) – иррациональная

дробь, необходимо умножить числитель и знаменатель дроби на выражение, сопряженное числителю.

Раскрытие неопределенностейРаскрытие неопределенностиЕсли f(x) – дробно – рациональная функция, необходимо разложить на множители числитель и знаменатель дробиЕсли

Слайд 26

Слайд 27Основные правила раскрытия неопределенностей вида
В процессе вычисления пределов

функций могут встретиться разные случаи:

Основные правила раскрытия неопределенностей вида В процессе вычисления пределов функций могут встретиться разные случаи:

Слайд 28 Прямую подстановку использовать нельзя в тех случаях,

когда мы не можем вычислить значение элементарной функции, стоящей под

знаком предела, в данной предельной точке .

Прямую подстановку использовать нельзя в тех случаях, когда мы не можем вычислить значение элементарной

Слайд 29Бывают неопределённости вида
Чтобы раскрыть неопределенность вида

, надо числитель и знаменатель дроби почленно разделить

на переменную в наивысшей степени.

Бывают неопределённости вида Чтобы раскрыть неопределенность вида , надо числитель и знаменатель

Слайд 30Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция или

иррациональная дробь необходимо разделить числитель и знаменатель дроби на x

в старшей степени

Раскрытие неопределенностейРаскрытие неопределенностиЕсли f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить числитель и знаменатель

Слайд 31 Замечание: если в числителе и знаменателе многочлены

одной степени, то предел равен отношению коэффициентов при старших

степенях, если же разной степени, но предел равен 0 или

Например:

Замечание: если в числителе и знаменателе многочлены одной степени, то предел равен отношению

Слайд 32Например:

Например:

Слайд 33Раскрытие неопределенностей
Раскрытие неопределенности
Умножим и разделим функцию на сопряженное выражение.

Раскрытие неопределенностейРаскрытие неопределенностиУмножим и разделим функцию на сопряженное выражение.

Слайд 34Упражнения:

Упражнения:

Слайд 35Упражнения:

Упражнения:

Слайд 36Упражнения:

Упражнения:

Слайд 37Домашнее задание:
Колесов В.В. Математика для медицинских колледжей: учебное пособие/В.В.Колесов, М.Н.

Романов. – Ростов н/Д: Феникс, 2015 – 316 с.: ил.-

(среднее медицинское образование). Гл.5. § 5.1-5.11
СВР: Подготовить реферативное сообщение на тему “Математика и медицина”
Используя презентацию и конспект : Заполнить тема 1.1.- Занятие 1 из Рабочей тетради для аудиторной работы по Математике

Домашнее задание:Колесов В.В. Математика для медицинских колледжей: учебное пособие/В.В.Колесов, М.Н. Романов. – Ростов н/Д: Феникс, 2015 –

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей