Геометрия - 7 Задачи на построение Учебник "Геометрия 7-9" Автор Л.С. Атанасян

Содержание

1. Геометрия - 7 Задачи на построение Учебник "Геометрия 7-9" Автор Л.С. Атанасян
2. В геометрии выделяют задачи
3. АВСПостроение угла, равного данному.Дано: угол А.ОDEТеперь докажем, что построенный угол равен данному.
4. Построение угла, равного данному.Дано: угол А.АПостроили угол
5. биссектрисаПостроение биссектрисы угла.
6. Докажем, что луч АВ – биссектриса
7. ВАПостроение перпендикулярных прямых.
8. Докажем, что а РМАМ=МВ, как радиусы
9. aNМПостроение перпендикулярных прямых.
10. aNBACМПосмотрим на расположение циркулей.АМ=АN=MB=BN, как равные радиусы. МN-общая сторона. MВN= MAN, по трем сторонам
11. Докажем, что О – середина отрезка АВ.Построение середины отрезка
12. ВАТреугольник АРВ р/б.Отрезок РО является биссектрисой, а
13. DСПостроение треугольника по двум сторонам и углу
14. DСПостроение треугольника по стороне и двум прилежащим
15. СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим
16. Скачать презентанцию

В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений. Линейка позволяет провести произвольную

Главная
Разное
Геометрия - 7 Задачи на построение Учебник "Геометрия 7-9" Автор Л.С. Атанасян

Слайды и текст этой презентации

Слайд 1Геометрия - 7
Задачи на построение
Учебник "Геометрия 7-9" Автор Л.С. Атанасян

Слайд 2 В геометрии выделяют задачи на построение, которые

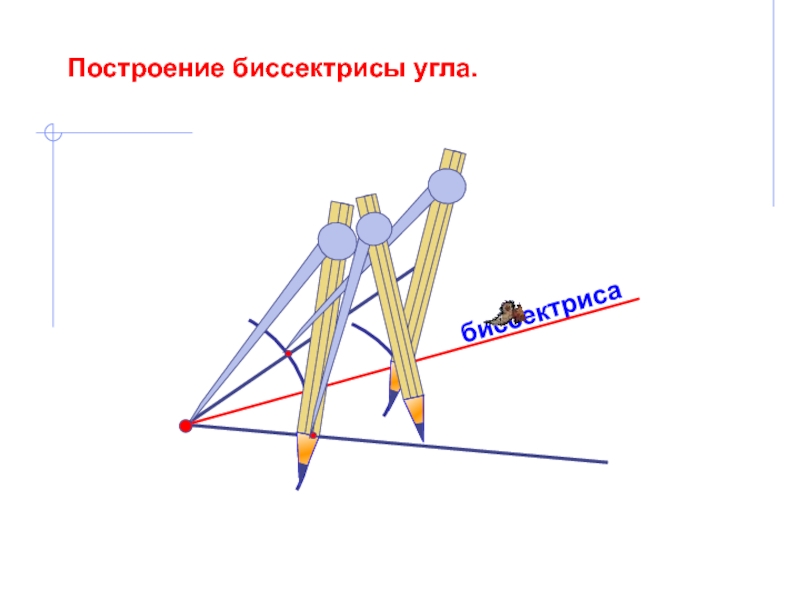
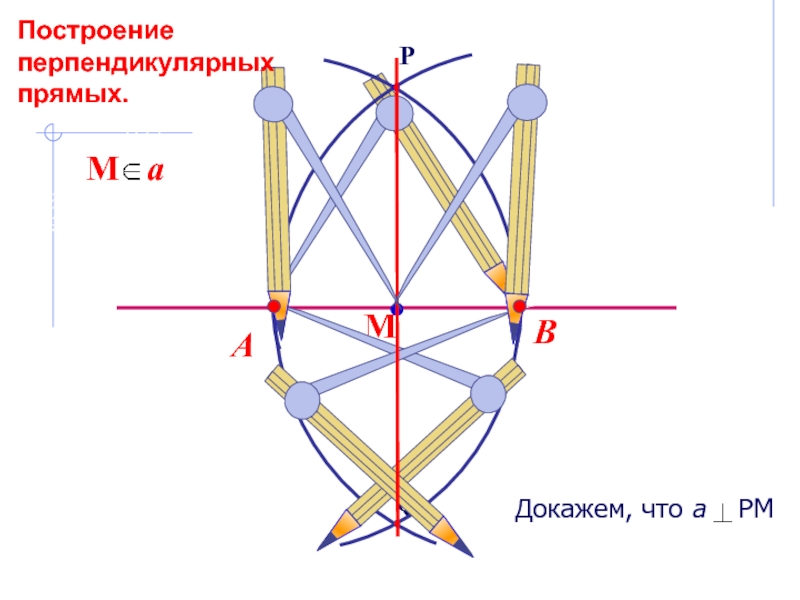
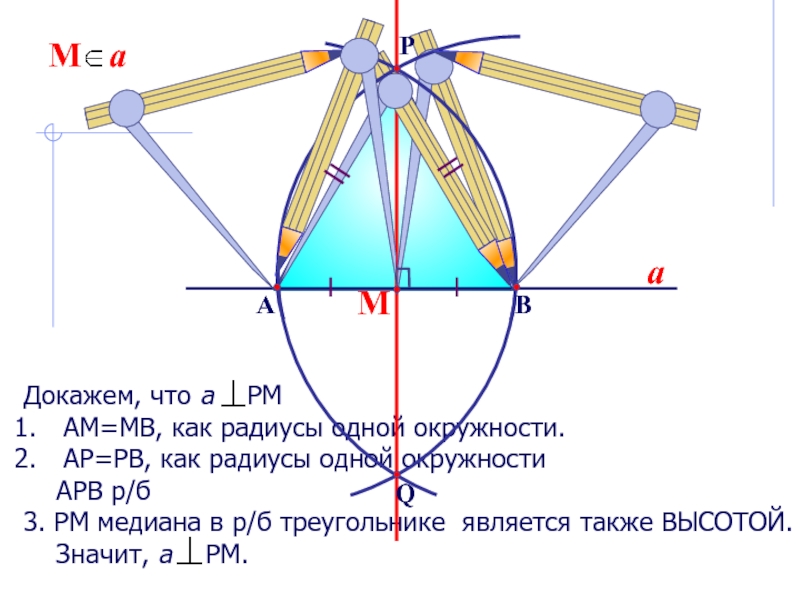
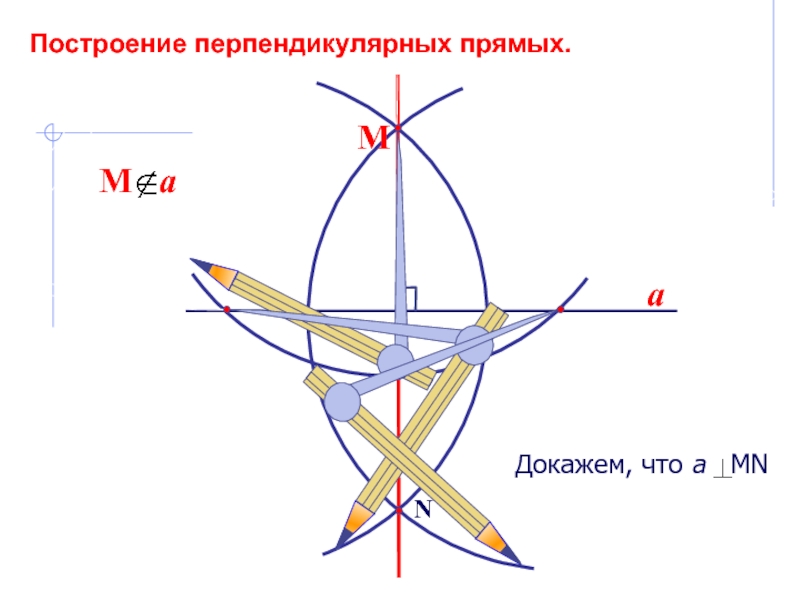
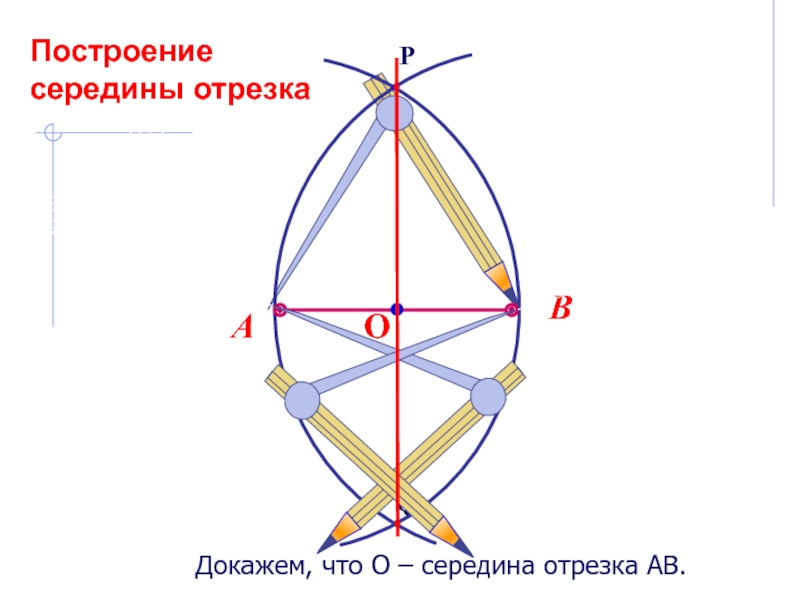
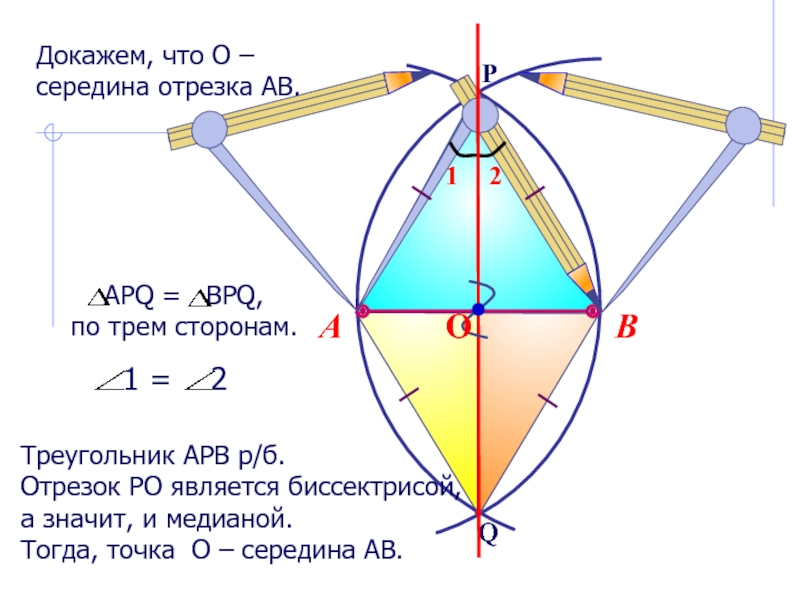
можно решить только с помощью двух инструментов: циркуля и линейки

без масштабных делений.

Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов:

Слайд 3А
В
С
Построение угла, равного данному.
Дано: угол А.
О
D
E
Теперь докажем, что построенный угол

равен данному.

Слайд 4Построение угла, равного данному.
Дано: угол А.
А
Построили угол О.
В
С
О
D
E
Доказать: А

= О
Доказательство: рассмотрим треугольники АВС и ОDE.
АС=ОЕ, как радиусы

одной окружности.
АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О

Построение угла, равного данному.Дано: угол А.АПостроили угол О.ВСОDEДоказать: А = ОДоказательство: рассмотрим треугольники АВС и

Слайд 5биссектриса
Построение биссектрисы угла.

Слайд 6Докажем, что луч АВ – биссектриса А

П Л А Н
Дополнительное построение.
Докажем равенство

треугольников ∆ АСВ и ∆ АDB.

3. Выводы

АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.

∆АСВ = ∆ АDВ, по III признаку
равенства треугольников

Луч АВ – биссектриса

Слайд 7В
А
Построение
перпендикулярных
прямых.

Слайд 8Докажем, что а РМ
АМ=МВ, как радиусы одной окружности.
АР=РВ, как

радиусы одной окружности
АРВ р/б
3. РМ медиана в р/б

треугольнике является также ВЫСОТОЙ.
Значит, а РМ.

Докажем, что а РМАМ=МВ, как радиусы одной окружности.АР=РВ, как радиусы одной окружности АРВ р/б3. РМ

Слайд 9a
N
М
Построение перпендикулярных прямых.

Слайд 10a
N
B
A
C
М
Посмотрим
на расположение
циркулей.

АМ=АN=MB=BN,
как равные радиусы.

МN-общая сторона.

MВN= MAN,
по трем сторонам

Слайд 11Докажем, что О – середина отрезка АВ.
Построение
середины отрезка

Слайд 12В
А
Треугольник АРВ р/б.
Отрезок РО является биссектрисой,
а значит, и медианой.

Тогда, точка О – середина АВ.
Докажем, что О –

середина отрезка АВ.

ВАТреугольник АРВ р/б.Отрезок РО является биссектрисой, а значит, и медианой. Тогда, точка О – середина АВ.Докажем,

Слайд 13D
С
Построение треугольника по двум сторонам и углу между ними.
Угол

hk
h
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному.
Отложим

отрезок АС, равный P2Q2.

Треугольник АВС искомый. Обоснуй, используя I признак.

Дано:

Отрезки Р1Q1 и Р2Q2

DСПостроение треугольника по двум сторонам и углу между ними. Угол hkhПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим

Слайд 14D
С
Построение треугольника по стороне и двум прилежащим к ней углам.

Угол h1k1
h2
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный

данному h1k1.
Построим угол, равный h2k2 .

Треугольник АВС искомый. Обоснуй, используя II признак.

Дано:

Отрезок Р1Q1

DСПостроение треугольника по стороне и двум прилежащим к ней углам. Угол h1k1h2Построим луч а.Отложим отрезок АВ, равный

Слайд 15С
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром

в т. А и
радиусом Р2Q2.
Построим дугу

с центром в т.В и
радиусом P3Q3.

Треугольник АВС искомый. Обоснуй, используя III признак.

Дано:

отрезки
Р1Q1, Р2Q2, P3Q3.

Построение треугольника по трем сторонам.

СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим дугу с центром в т. А и

Скачать презентацию

Разделы презентаций

Геометрия - 7 Задачи на построение Учебник "Геометрия 7-9" Автор Л.С. Атанасян

Содержание

Слайды и текст этой презентации

Слайд 1Геометрия - 7
Задачи на построение
Учебник "Геометрия 7-9" Автор Л.С. Атанасян

Слайд 2 В геометрии выделяют задачи на построение, которые

можно решить только с помощью двух инструментов: циркуля и линейки