Слайд 1ГИДРОЦИКЛОНИРОВАНИЕ
Старший преподаватель
Львов Владимир Анатольевич
курс лекций
Слайд 2Основная литература:
Фролов Ю. Г. Курс коллоидной химии. Поверхностные явления и
дисперсные системы. – М. Химия, 1988. – 464 с.
Разделение
суспензий в химической промышленности/ Малиновская Т. А. и др. – М. Химия, 1983. – 264 с.
Протодьяконов И. О., Люблинская И. Е., Рыжков А. Е. Гидродинамика и массообмен в дисперсных системах жидкость – твердое тело. – Л.: Химия, 1987. – 336 с.
Дополнительная литература:
Терновский И. Г., Кутепов А. М. Гидроциклонирование. – М.: Наука, 1994. – 350 с.
Протодьяконов И. О., Чесноков Ю. Г. Гидромеханические основы процессов химической технологии. – Л.: Химия, 1987. – 360 с.
учебно-методические материалы
Слайд 3ЛЕКЦИЯ 1. Выбор оборудования и материалов для разделения дисперсных систем.
Свойства разделяемой дисперсной системы.
Требования к конечному продукту и шламу.
Особенности производства.
Технологические
возможности конструкций оборудования.
Свойства разделяемой дисперсной системы
В эту группу обычно включают физические и химические свойства дисперсной системы, (агрессивность, взрывоопасность, летучесть, токсичность), термодинамические параметры процесса и их возможные изменения (обычно задаются технологами и очень редко меняются специалистами по разделению), специфические свойства, от которых зависит скорость и эффективность процессов разделения, и качество конечного продукта.
Основные группы общих положений и определяющих факторов
Слайд 4Требования к конечному продукту и шламу
Основной характеристикой является полнота разделения
(допустимое содержание жидкой фазы в осадке (песках) и твердой фазы
в выходе (фильтрате).
Замечание: Обычно эти требования задаются технологами и не подлежат изменению.
Особенности производства
Основными характеристиками здесь являются - заданная мощность производства (необходимая часовая производительность), периодичность или непрерывность технологической схемы производства, способы дальнейшей переработки продуктов, особые условия в цехе (его категорийность, площадь, высота и т.п.).
Технологические возможности конструкций
оборудования
Основу составляют движущая сила, конструктивные особенности, взрывопожарозащищенность, герметичность, применяемые материалы.
Замечание: При решении задач оптимизации необходимо также учитывать удобство обслуживания, надежность работы и технико-экономические показатели. Изменение хотя бы одного фактора может привести не только к изменению характеристик процесса или числа единиц оборудования, но и его типа.
Слайд 5Внимание!!! Для однозначного определения и фиксации всех факторов, составление развернутого
ТЗ является обязательным.
Примерная последовательность
при выборе и расчете оборудования
Анализ
опросного листа-задания (ТТ) разработчика технологии или регламента действующего (нового) производства. Изучение требований, предъявляемых к конечным продуктам, особенностей производства, физических и химических свойств разделяемой дисперсной системы.
Замечание: Данный этап обычно заканчивается расчетом требуемой часовой мощности производства на стадии разделения дисперсной системы.
Определение физико-химических свойств разделяемой дисперсной системы (скорости осаждения, дисперсности и т.п.).
Замечание: Производится по результатам предварительного экспериментального обследования.
Слайд 6Выбор процесса разделения дисперсной системы: осаждение, фильтрование, центробежная очистка (фильтрование
и/или осаждение в центробежном поле).
Замечание: Осуществляется на основе опыта предшествующих
разработок и объективных, исходных количественных данных.
Оценочный расчет производительности аппаратов и сопоставление полученных результатов с требованиями, предъявляемыми к конечному продукту (включая экспериментальные результаты).
Замечание: Заканчивается выбором способа создания движущей силы (перепада давления, разряжения, безнапорного течения, турбины и т.п.) и оценкой возможных вариантов аппаратного оформления процесса.
Решение задачи оптимизации с точки зрения движущей силы с использованием дополнительных данных (экспериментальных, модельных, справочных, каталожных) и определение оптимальных режимов разделения дисперсной системы, включая границы их возможного изменения.
Замечание: Завершается большим количеством возможных вариантов технических решений.
Осуществление выбора конструкционных материалов, включая анализ возможности требований коррозионной и абразивной защиты, герметичности, взрывопожаробезопасности и т.п. выпускаемого оборудования.
Замечание: Заканчивается существенным сокращением возможных вариантов аппаратного и конструктивного оформления процессов.

Слайд 7Проведение экспериментов на лабораторных установках, моделирующих работу промышленного оборудования. Основная
цель – проверка работоспособности отдельных узлов и конструкций выбранного оборудования
применительно к свойствам разделяемой дисперсной системы.
Замечание: Заканчивается подтверждением или исключением предлагаемого варианта аппаратного и конструктивного оформления.
Определение рациональных (оптимальных) режимов работы, обеспечивающих максимальную эффективность (производительность), для выбранных вариантов оборудования, при заданном качестве продуктов разделения.
Замечание: Определение осуществляется на модельной установке экспериментально-расчетным путем с учетом условий конкретной работы данного производства.
Выявление условий воспроизводимости технологического процесса, включая границы применимости.
Замечание: Оценки осуществляются экспериментально-статистическим методом в модельных и/или промышленных условиях.
Слайд 8Оценка экспериментально-расчетным методом ресурсных характеристик, включая снижение расчетных параметров.
Замечание: Заканчивается
определением периодичности обслуживания, регламента и т.п.
Расчет характеристик выбранных типов оборудования
с учетом рекомендованных режимов работы и свойств разделяемой дисперсной системы.
Замечание: Заканчивается технико-экономическим сравнением вариантов аппаратного оформления.
Полный технологический расчет технологического цикла, включая основное и вспомогательное оборудование.
Замечание: Завершается оформлением рекомендаций для проектирования.
Собственно проектирование и компоновка оборудования.
Замечание: Завершается выпуском комплекта рабочих чертежей.
Изготовление, комплектация и сборка отдельных единиц оборудования.
Замечание: Завершается приемо-сдаточными испытаниями отдельных элементов оборудования.
Слайд 9Опытно-промышленная проверка выбранных или разработанных единиц оборудования.
Замечание: Осуществляется для
уточнения масштабного перехода, особенно для многотоннажного производства.
Монтаж и проведение пуско-наладочных
работ.
Замечание: Завершается актом приемо-сдаточных испытаний.
Опытно-промышленная проверка характеристик системы
Замечание: Завершается актом приемки выполненных работ.
Оценка эксплуатационных характеристик оборудования.
Замечание: Осуществляется экспериментально-статистическим методом в процессе эксплуатации оборудования.
Вывод: Составление развернутого ТЗ и подписание его обеими сторонами договорных отношений, на начальной стадии работ, позволяет избежать не обоснованных затрат со стороны исполнителя и исключить потери заказчика.
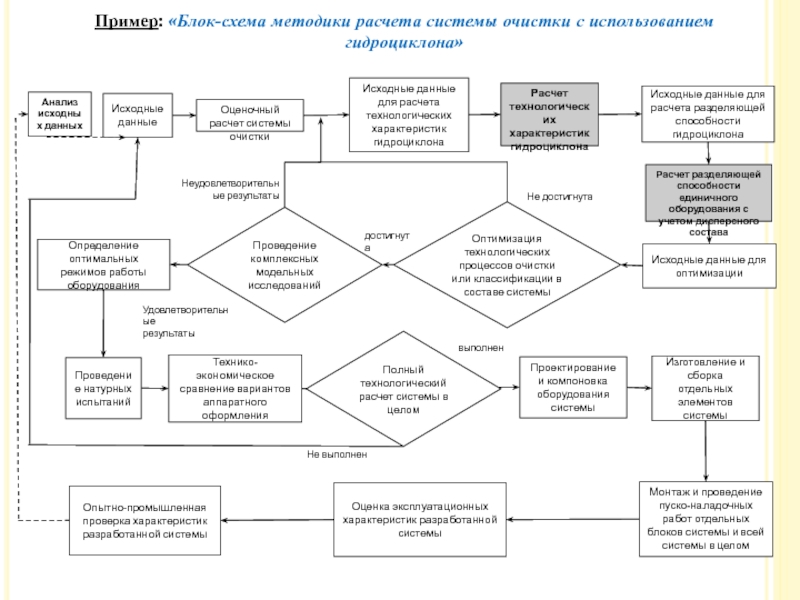
Слайд 10Анализ исходных данных
Исходные данные
Оптимизация технологических процессов очистки или классификации в
составе системы
Исходные данные для расчета разделяющей способности гидроциклона
Оценочный расчет системы
очистки
Расчет разделяющей способности единичного оборудования с учетом дисперсного состава
Исходные данные для оптимизации
Определение оптимальных режимов работы оборудования
Проведение комплексных модельных исследований
Проектирование и компоновка оборудования системы
Технико-экономическое сравнение вариантов аппаратного оформления
Проведение натурных испытаний
Изготовление и сборка отдельных элементов системы
Оценка эксплуатационных характеристик разработанной системы
Опытно-промышленная проверка характеристик разработанной системы
Монтаж и проведение пуско-наладочных работ отдельных блоков системы и всей системы в целом
Расчет технологических
характеристик
гидроциклона
достигнута
Неудовлетворительные результаты
Удовлетворительные
результаты
Не достигнута
Пример: «Блок-схема методики расчета системы очистки с использованием гидроциклона»
Полный технологический расчет системы в целом
выполнен
Не выполнен
Исходные данные для расчета технологических
характеристик гидроциклона
Слайд 11Лекция 2. Основные виды классификаций свободнодисперсных систем
F=K-Ф+2 и F=K-Ф+3
F – число степеней
свободы, К - число компонентов в системе, Ф – число
фаз, 2 - два независимых параметра (давление и температура), 3 - три параметра, один из которых дисперсность.
Общая классификация свободнодисперсных систем
Грубодисперсные – с размером частиц более 100 мкм,
Тонкодисперсные – с размером частиц от 100 до 0,5 мкм,
Мути – с размером частиц то 0,5 мкм до 100 нм,
Золи (коллоидные растворы) – качественно отличающийся вид дисперсных систем – с размером частиц менее 100 нм.
Вывод: При выборе метода разделения дисперсных систем, одним из основных параметров является их дисперсность.
Правило фаз Гиббса для дисперсных систем
Слайд 12Основные классификации фазового состояния
и дисперсности систем
Общая классификация дисперсных систем
в технологических производствах
Грубодисперсные (суспензии, эмульсии, порошки, взвеси и т.д.) с
размером частиц 10-6 – 10-3 м и более.
Коллоидно-дисперсные (коллоидные) с размером частиц 10-9 – 10-6м. К ним относятся золи (гидрозоли, органозоли, аэрозоли), растворы полимеров и т.д.
Молекулярные или ионные (истинные) растворы с размером частиц менее 10-9 м.
Вывод: применительно к рассматриваемой проблеме представленная классификация носит слишком общий характер, поскольку не позволяет производить объективного выбора и расчета того или иного технологического (промышленного) метода очистки воды в конкретных условиях.
Слайд 13Детальная классификация дисперсных систем
в технологических процессах
Грубодисперсные – с размером
частиц более 10-5 м
Среднедисперсные – с размером частиц 10-5 –
10-7 м
Высокодисперсные – с размером частиц 10-7 – 10-9 м
Молекулярно-дисперсные – с размером частиц менее 10-9 м
Вывод: Применительно к процедуре выбора метода очистки воды и методики его расчета данная классификация также является ограниченной, поскольку не учитывает специфических особенностей загрязнений гидросферы.
Основные классификации фазового состояния
и дисперсности систем
Слайд 14Классификация дисперсных систем в гидросфере
С размером частиц 10-5 – 10-7
м и более. К этой группе относятся нерастворимые вещества, образующие
грубодисперсные примеси, в виде суспензий или эмульсий, а также планктон и патогенная микрофлора, находящаяся в воде во взвешенном состоянии. Проникновение их в водоемы осуществляется естественной эмиссией и антропогенным путем со сточными водами промышленных, сельскохозяйственных и коммунальных предприятий
С размером частиц 10-7 – 10-8 м. Эта группа представляет собой гидрофильные коллоидные частицы почв, грунтов, гуминовые и фульвокислоты, которые вымываются водой из лесных, торфяных и болотистых почв, а также высокомолекулярные вещества техногенного происхождения
С размером молекул 10-8 – 10-9 м. Эта группа включает растворенные в воде газы, органические и слабо диссоциированные неорганические соединения
С размером загрязнений менее 10-9 м. Образуют в воде молекулярные или ионные (истинные) растворы. Вещества этой группы представлены сильными электролитами (соли, кислоты, основания).
Вывод: Данная классификация наиболее полно отражает реальные потребности специалистов в области защиты окружающей среды. На ее основе становится возможным обоснованный выбор необходимого метода очистки воды и нахождение расчетных зависимостей с учетом фазово-дисперсных состояний загрязняющих веществ.

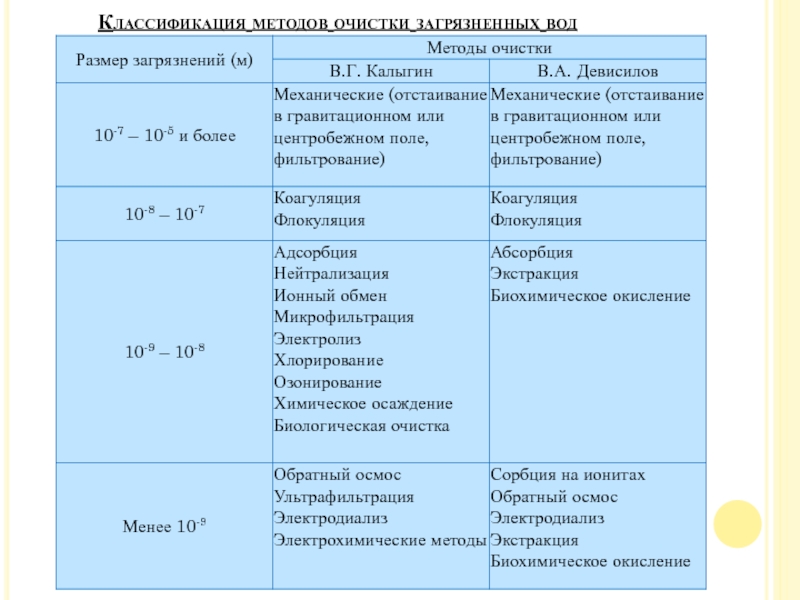
Слайд 15Классификация методов очистки загрязненных вод
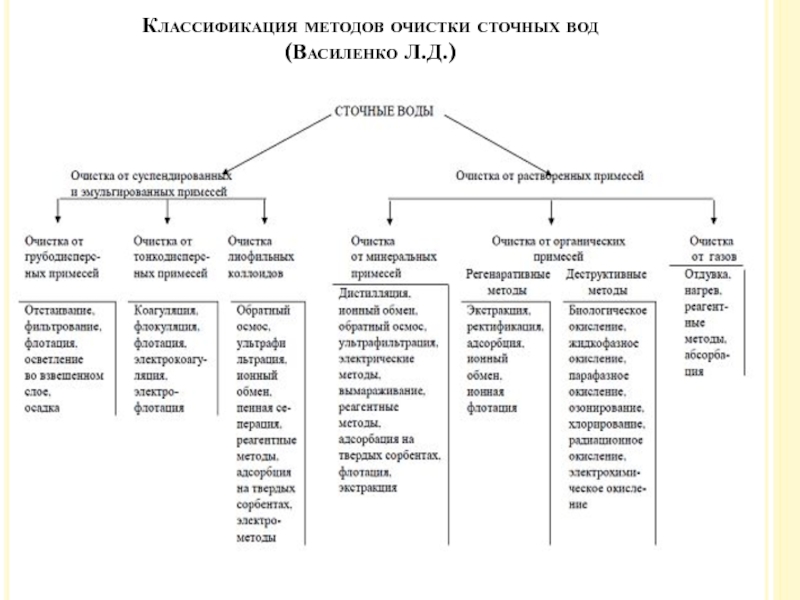
Слайд 16Классификация методов очистки сточных вод
(Василенко Л.Д.)
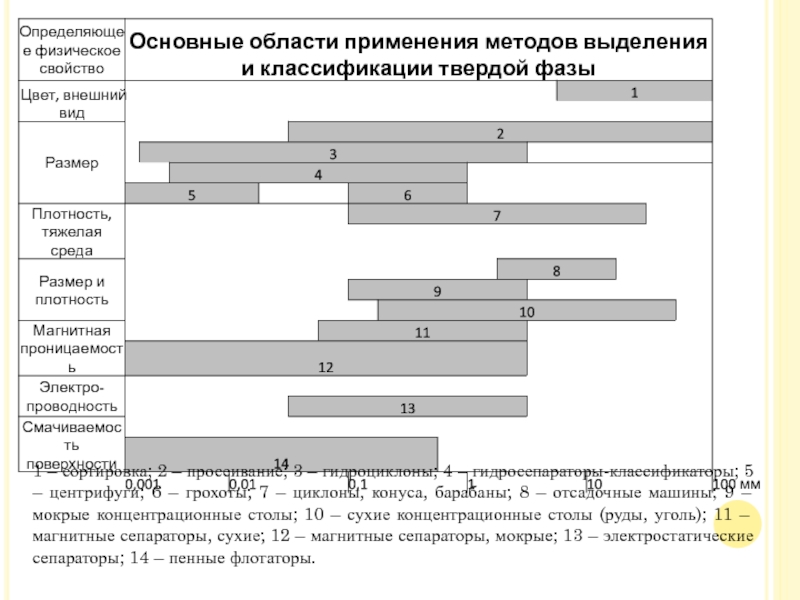
Слайд 171 – сортировка; 2 – просеивание; 3 – гидроциклоны; 4
– гидросепараторы-классификаторы; 5 – центрифуги; 6 – грохоты; 7 –
циклоны, конуса, барабаны; 8 – отсадочные машины; 9 – мокрые концентрационные столы; 10 – сухие концентрационные столы (руды, уголь); 11 – магнитные сепараторы, сухие; 12 – магнитные сепараторы, мокрые; 13 – электростатические сепараторы; 14 – пенные флотаторы.
Слайд 18Лекция 3. Теоретические основы разделения дисперсных систем
Седиментация
Условия:
Оседания -
Всплытия -
Плавания
внутри жидкости –
где Fg – сила тяжести, Fa – сила
Архимеда, Fсеd – движущая сила процесса седиментации, V – объем частицы, m – масса частицы, ρ – плотность частиц дисперсной фазы, ρ0 – плотность дисперсионной среды, g – ускорение свободного падения.
Слайд 19При ламинарном движении частиц:
Для стоксовской частицы:
Способность к седиментации выражается через
константу седиментации, которая определяется скоростью седиментации:
Для сферических частиц эта константа
равна:
Справочно: Единица измерения – Сведберг (Сб =10-13 с).
Кварц в воде 10-5м = 10мкм S = 325 МСб =3,25*10-5с.
Вывод: Константа седиментации зависит не только от размеров частиц, но и от природы фаз.
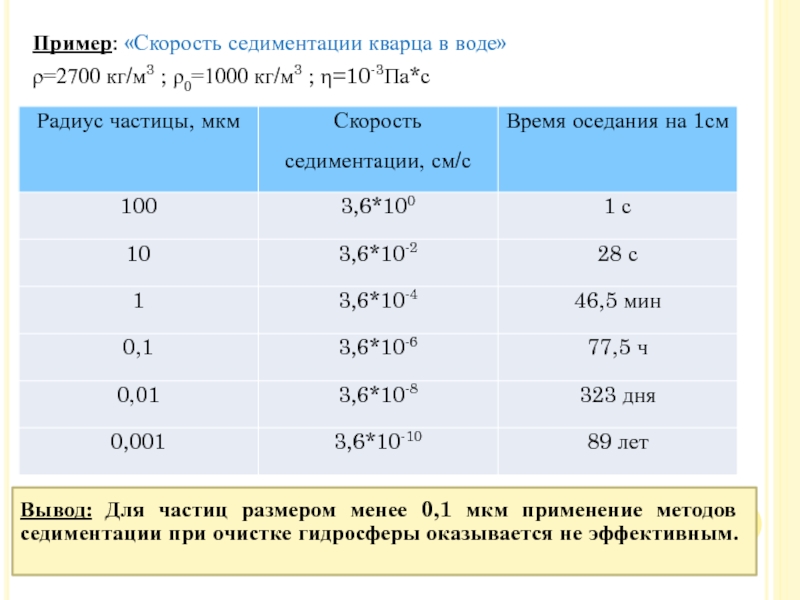
Слайд 20Пример: «Скорость седиментации кварца в воде»
ρ=2700 кг/м3 ; ρ0=1000 кг/м3
; η=10-3Па*с
Вывод: Для частиц размером менее 0,1 мкм применение методов
седиментации при очистке гидросферы оказывается не эффективным.
Слайд 21Внимание! Единичная частица всегда осядет! Учет диффузии необходим только в
том случае, когда дисперсная система представляет собой статистическое множество частиц.
Замечание: При наличии статистического множества частиц оседание приводит к уменьшению их частичной концентрации ν в верхних слоях и увеличению в нижних, т.е. к возникновению градиента концентраций dν/dx.
В соответствии с первым законом Фика:
Количество дисперсной фазы, перенесенное за время τ за счет диффузии, с учетом уравнения Эйнштейна
Градиент концентрации вызывает диффузионный поток (снизу вверх):
При наличии седиментационного потока (сверху вниз):
Вывод: Характер поведения частиц в дисперсных системах определяется их размером и разностью плотностей. Чем больше разность, тем значительней влияние седиментации на тепловое движение частиц.
Условие седиметационно-диффузионного равновесия
Слайд 22Замечание: С увеличением размера частиц быстро растет поток седиментации ic
≈ r2 и снижается диффузионный поток iD ≈ 1/r.
Вывод:
Если iD >> ic (ультрамикрогетерогенные системы) седиментацией можно пренебречь, в противном случае (микрогетерогенные системы) диффузию можно не учитывать.
Внимание! В грубодисперсных системах (10…40 мкм и более) седиментация идет, как правило, с ускорением.
Справочно: Коэффициент диффузии:
для коллоидных частиц D = 5*10-9 см2/с,
для растворов в воде 0,3…1,1*10-5 см2/с,
для газов в воздухе 0,1…0,7 см2/с.
Вывод: Соотношение между диффузией и седиментацией служит одной из основ для классификации дисперсных систем по дисперсности.
Условие седиметационно-диффузионного равновесия
Слайд 23Пусть iD = ic - условие седиментационно-диффузионного равновесия. Исходя из
опыта Перрена
В поле действия центробежных сил также достигается седиментационно-диффузионное
равновесие:
Справочно: При ν/ν0=2 характерная высота составляет:
для газов в атмосфере 5…5,5 км,
для полимеров порядка - 20 м,
для золей золота - 2,15 м,
для микронных частиц ~10 мкм.
Вывод: В сосудах обычных размеров концентрация грубо- и мелко- дисперсной фазы практически не изменяется по высоте.
Условие седиметационно-диффузионного равновесия
Слайд 24Замечание: Если сравнить седиментацию при наличии диффузии и без нее,
то обращает на себя внимание различие факторов, обеспечивающих устойчивость дисперсных
систем к осаждению – седиментационную устойчивость.
Вывод: Различают кинетическую седиментационную устойчивость (КСУ) и термодинамическую седиментационную устойчивость (ТСУ).
Внимание! Для ТСУ характерно термодинамическое равновесие, которого может и не быть при КСУ. ТСУ обуславливается статическими законами диффузии и непосредственно связана с седиментационно-диффузионным равновесием.
Мерой КСУ является величина обратная константе седиментации:
КСУ=1/Sced =B/mot = 9η/ 2r2(ρ-ρ0) - обратный Сведберг =1013с-1
Мерой ТСУ является гипсометрическая высота, которую удобно определять как:
Вывод: Гипсометрическая высота и ТСУ не зависят от вязкости среды, а повышение температуры способствует устойчивости. КСУ с повышением температуры обычно снижается из-за уменьшения вязкости.
Условие седиметационно-диффузионного равновесия
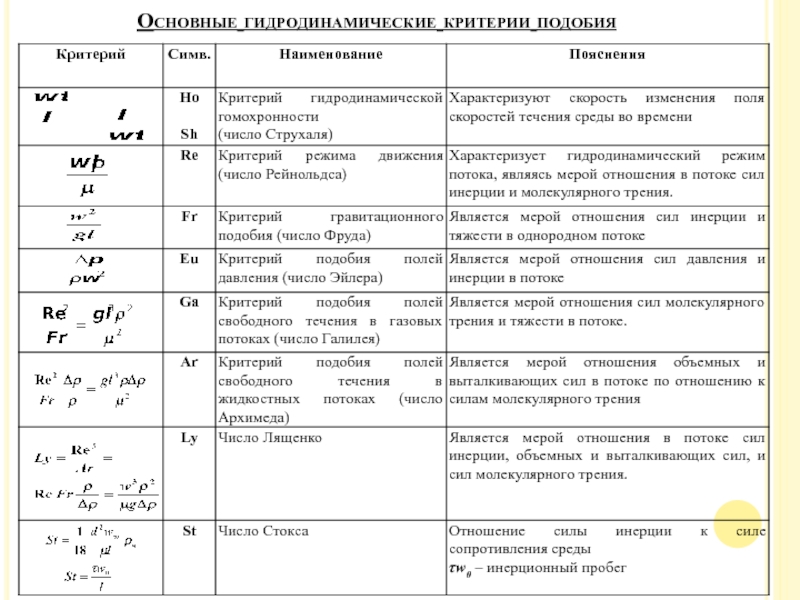
Слайд 25Основные гидродинамические критерии подобия
Слайд 26Примечание: Для более точных расчетов можно использовать формулы, сведенные в
таблицу
Применение закона Ньютона-Риттенгера
Закон Ньютона-Риттенгера:
где λ – коэффициент сопротивления; S –
площадь проекции частицы на плоскость, перпендикулярную направлению движения (для сферы S=πd2/4); ψ =λπ/8 – фактор сопротивления; u – скорость осаждения.
Fr = u2/dg – число Фруда
Замечание: Для ламинарного режима величина ψ зависит от режима относительного движения твердой частицы в жидкости, т.е. от Re = udρ/η.
При ψ =3π/Re, u=d2∆ρg/18η
Для турбулентного режима значение фактора сопротивления ψ не зависит от Re и равно 0,17.
Вывод: Это и есть искомое уравнение Ньютона-Риттенгера
Для всех режимов осаждения в рамках проведения инжереных расчетов:
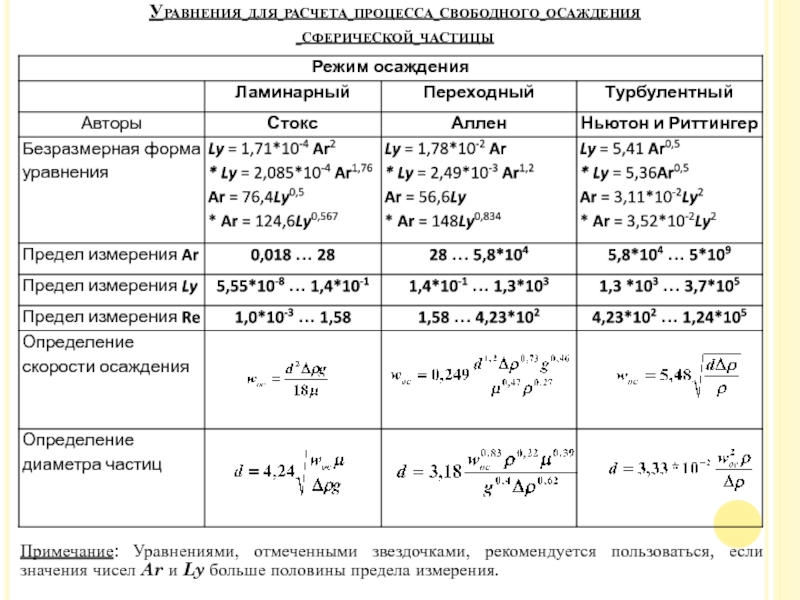
Слайд 27Уравнения для расчета процесса свободного осаждения
сферической частицы
Примечание: Уравнениями, отмеченными
звездочками, рекомендуется пользоваться, если значения чисел Ar и Ly больше
половины предела измерения.
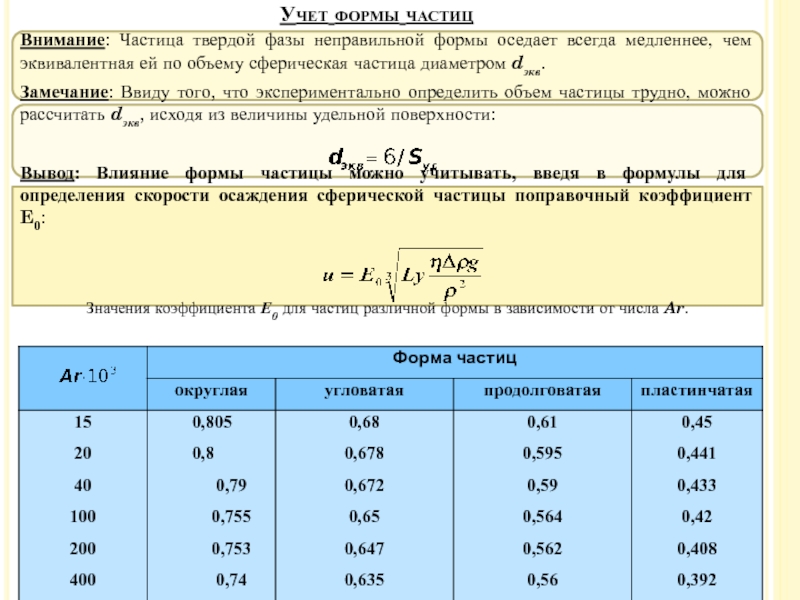
Слайд 28Внимание: Частица твердой фазы неправильной формы оседает всегда медленнее, чем
эквивалентная ей по объему сферическая частица диаметром dэкв.
Замечание: Ввиду того,
что экспериментально определить объем частицы трудно, можно рассчитать dэкв, исходя из величины удельной поверхности:
Вывод: Влияние формы частицы можно учитывать, введя в формулы для определения скорости осаждения сферической частицы поправочный коэффициент E0:
Значения коэффициента Е0 для частиц различной формы в зависимости от числа Ar.
Учет формы частиц
Слайд 29Учет стесненного осаждения
Замечание: При увеличении содержания твердой фазы в суспензии
свободное осаждение переходит в стесненное и коллективное.
Вывод: В этом случае
сопротивление, оказываемое жидкостью частицам твердой фазы, зависит от их содержания в суспензии.
Влияние содержания твердой фазы суспензии cv на сопротивление движущимся частицам учитывается введением в уравнение закона Ньютона-Реттингера функции пористости:
Для имеем:
Внимание! Процесс осаждения концентрированной суспензии, т.е. движение твердой фазы относительно жидкой, иногда рассматривают как движение жидкой фазы относительно твердой, т.е. как движение жидкости через пористую среду.
Если учесть, что где Р – давление слоя суспензии высотой δ, преодолевающее силы трения жидкости при ее движении относительно твердой фазы, то получаем уравнение Козени-Кармана.
– удельное сопротивление осадка
где А’, A” – const; ψ – коэффициент, зависящий от формы частиц.
Слайд 30Лекция 4. Теоретические основы разделения дисперсных систем. Движение по окружности.
Центрифугирование
Вывод: Строго говоря, равновесие сил, действующих на частицу, при центробежном
осаждении не может наступить, т.к. всегда будет соблюдаться условие Fсеd > Fтр.
Замечание: В инженерных расчетах определяется максимально возможная скорость центробежного осаждения, которую можно найти исходя из условия Fсеd = Fтр
При ламинарном движении , В – коэффициент трения.
Для стоксовских частиц:
Слайд 31Используя закон Ньютона-Риттенгера, получаем:
Для ламинарного, турбулентного и переходного режимов имеем:
где
- фактор разделения (аналог числа Фруда)
Внимание! Соотношения, описывающие закономерности осаждения в центробежном поле, сходны с соответствующими соотношениями гравитационного осаждения. Различие заключается лишь в том, что в первом случае в формулы входит центробежное ускорение, а во втором – ускорение силы тяжести.
При центробежном осаждении для чисел Архимеда (Ar’) и Лященко (Ly’) получаем:
Произведение этих чисел равно произведению чисел Архимеда (Ar) и Лященко (Ly)
Вывод: Для расчетов процесса центробежного осаждения можно использовать безразмерные уравнения для процесса седиментации, подставляя в них значения Ar’ и Ly’.
Движение частиц по окружности
Слайд 32Расчетные зависимости методов очистки
Седиментация
g
Очистка в центробежном поле
При ламинарном движении частиц
Стоксовские
частицы
Слайд 33Особенности движения частиц по окружности
Пример: Определить предельные диаметры частиц d1
и d2, для которых применимы законы свободного осаждения Стокса и
Ньютона-Реттингера.
Кризис ламинарного осаждения наступает при
Переход к турбулентному осаждению осуществляется при
Для этих значений соответственно имеем:
при гравитационном осаждении:
при центробежном осаждении:
Вывод: Предельные диаметры в центробежном поле в раз меньше, чем в гравитационном.
Замечание: Частица, осаждающаяся по турбулентному закону в центрифуге с , в гравитационном поле будет оседать в ламинарном режиме.
Внимание! В промышленной практике в центробежном поле обычно разделяют полидисперсные и концентрированные суспензии при стесненном осаждении.
Скорость такого процесса должна быть в раз меньше, чем при свободном осаждении. Однако коагуляция может увеличить скорость процесса.
Слайд 34Замечание: Ввиду того, что теория процесса разделения полидисперсных концентрированных суспензий
еще не достаточно разработана, для решения практических вопросов следует прибегать
к эксперименту, базирующемуся на процессах моделирования.
Моделирование процессов разделения осуществляется путем обеспечения их подобия в экспериментальных условиях за счет:
Равенства чисел Фруда модели и натуры, точнее, обеспечивая равенство отношений , для чего создают пропорциональность скорости течения величине .
Выполнения равенства чисел Рейнольдса, т.е. искусственный загрязнитель, выбирают со средним диаметром обратно пропорциональным , при одинаковой плотности частиц.
Выполнения равенства т.е. пропорциональность величине ( )3
Выполнение условий одинаковости средней объемной концентрации С0.
Вывод: Следовательно, определяющими в процессе моделирования можно считать величины:
Особенности моделирования процессов разделения полидисперсных концентрированных суспензий
Слайд 35Центрифугирование
Справочно: Центрифугирование – разделение неоднородных систем (напр., жидкость – твердое
тело) при помощи центробежных сил. Применяется для разделения суспензий, осветления
загрязненных жидкостей, гидравлической классификации шламов по крупности твердых частиц и т.п.
Процесс центрифугирования осуществляется в центрифугах, основная рабочая часть которых - быстро вращающийся вокруг своей оси барабан (ротор).
По направлению движения жидкости во вращающемся роторе центрифуги подразделят на:
Трубчатые, очищаемый поток движется параллельно оси ротора;
Тарельчатые, очищаемый поток движется в плоскости наклонной (перпендикулярной) оси ротора (в радиальном направлении);
Прочее, с более сложным движением, например, шнековые.
По конструкции центрифуги обычно подразделяют на:
Осадительными (со сплошными стенками);
Фильтрующими (с перфорированными стенками, покрытыми тканью или ситами);
Комбинированные.
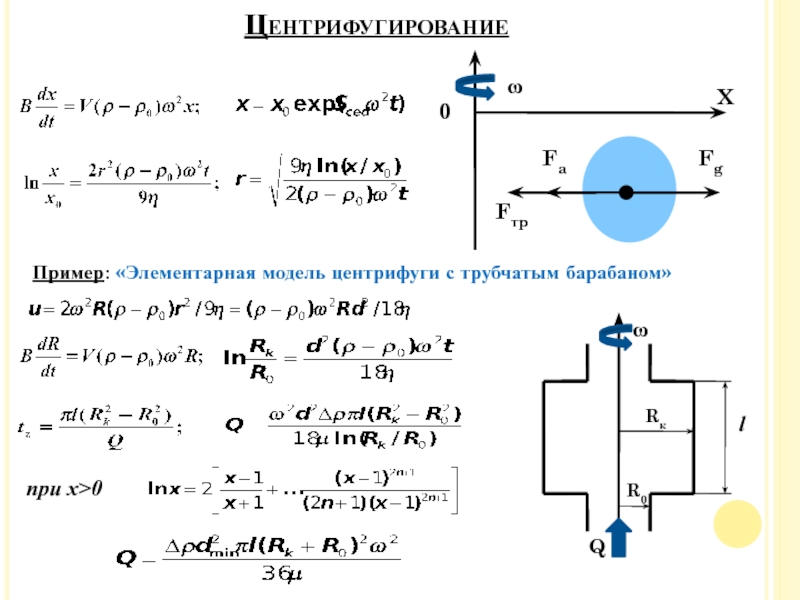
Слайд 36Пример: «Элементарная модель центрифуги с трубчатым барабаном»
Центрифугирование
l
Rк
R0
ω
Q
при х>0
Слайд 37Основные преимущества центрифуг по сравнению с механическими фильтрами:
Увеличение тонкости очистки
по мере возрастания частоты вращения ротора центрифуги.
Замечание: При очень
высокой тонкости очистки возможен выигрыш в трудоемкости и затратах на очистку.
Более высокая тонкость очистки при большом расходе жидкости.
Замечание: Центрифуги становятся конкурентоспособными при очистке частиц меньше 12 мкм.
Во много раз большая грязеёмкость, что в сотни раз увеличивает ресурс работы центрифуги.
Простота удаления осадка и возможность автоматизации процесса.
Удаление в первую очередь частиц с большой плотностью, т.е. наиболее абразивных.
Возможность отделения воды и воздуха.
Нечувствительность к смолистым образованиям.
Постоянство перепада давления и пропускной способности.
Возможность совмещения с насосами, обеспечивающую тонкую очистку на всасывании.
Центрифугирование
Слайд 38Внимание! Многие, но далеко не все, недостатки центрифуг могут быть
скомпенсированы за счет их конструктивного оформления.
Пример: «Модель тарельчатой центрифуги»
где z
– число межтарельчатых зазоров, расстояние между которыми Δz =0,7…0,8 мм, α - угол наклона тарелок к вертикали.
Основные недостатки центрифуг, ограничивающие область их применения:
Наличие подвижных частей и сложность конструкции, уплотнений и привода, особенно при больших угловых скоростях (ω > 500 рад/с).
Необходимость балансировки, высокая трудоемкость изготовления, больше габариты и масса.
Большие затраты энергии на привод при работе в затопленном состоянии.
Малая величина давления на сливе.
Вывод: Многие модели гидроциклонов могут составлять конкуренцию не только отстойникам, но и центрифугам.
Центрифугирование
Слайд 39Лекция 5. Гидроциклонирование
Справочно: Гидроциклонирование - разделение неоднородных систем (напр., жидкость
– твердое тело) при помощи центробежных сил, возникающих за счет
тангенциального движения жидкостного потока.
Применяется для разделения суспензий, эмульсий, осветления загрязненных жидкостей, гидравлической классификации шламов по крупности твердых частиц и т.п.
Процесс гидроциклонирования осуществляется в гидроциклонах, основные подходы к разработке которых базируются, в первую очередь, на различиях в их целевом назначении.
По этому признаку гидроциклоны обычно подразделяют на следующие основные группы:
гидроциклоны для проведения массообменных процессов;
гидроциклоны для разделения эмульсий и несмешивающихся жидкостей;
гидроциклоны-осветлители;
гидроциклоны-сгустители;
гидроциклоны-классификаторы.
Слайд 40Основные группы гидроциклонов
Замечание: Аппараты первых двух групп имеют свои специфические
особенности и, образуя самостоятельные направления в технике гидроциклонирования, в настоящем
курсе лекций детально не анализируются.
Гидроциклоны-осветлители преимущественно используются для очистки сред от твердых включений при обработке сточных вод, а также в технологических процессах, связанных с очисткой целевых жидкостей от сопутствующей твердой фазы.
Гидроциклоны-сгустители применяются для выделения твердой фазы из суспензий и пульп и сгущения ее до высоких концентраций порядка 50-70%.
Гидроциклоны-классификаторы в основном предназначены для фракционного разделения в жидкостных потоках твердых частиц и зернистых материалов по крупности.
Вывод: Для решения экологических задач в том или ином виде все группы гидроциклонов находят все более широкое применение при обработке, очистке, разделении, обогащении, сгущении, осветлении и классификации самых разнообразных по составу и свойствам водных дисперсных систем.
Слайд 41Основные типы конструкций гидроциклонов
турбоциклоны;
Замечание: Использование турбоциклонов в промышленной
экологии сдерживается целым рядом обстоятельств. При этом применение аппаратов указанного
типа при решении экологических задач в настоящее время следует признать недостаточно обоснованным.
конические;
Замечание: Конические гидроциклоны имеют в промышленной экологии весьма ограниченную область применения, поскольку главным образом предназначены для разделения лишь грубых суспензий.
цилиндрические (прямоточные и противоточные);
Замечание: Цилиндрические гидроциклоны используют чаще всего для проведения процессов двухфракционной или многофракционной классификации, осветления и сгущения суспензий. Однако при решении экологических задач вопрос обоснованного их применения является неоднозначным, поскольку разделение по крупности твердой фазы в данных аппаратах происходит не достаточно четко.
цилиндроконические.
Вывод: Гидроциклоны цилиндроконического типа применяют для осветления, сгущения, обогащения и классификации разнообразных водных суспензий. Эти аппараты нашли наиболее широкое применение в различных отраслях промышленности и экологии.

Слайд 42Эрозионный износ внутренних поверхностей при длительной эксплуатации.
Замечание: Этот недостаток устраняется
за счет соответствующего выбора конструкционных материалов и защитных покрытий.
Изменение показателей
разделения при колебаниях расхода, концентрации и состава твердой фазы в питании аппарата;
Этот недостаток устраняется за счет:
Введения дополнительных конструктивных элементов;
Основные недостатки гидроциклонов и
пути их устранения
а) с осевым вводом разделяемой смеси и винтовым коробом для вывода промежуточного продукта;
а)
б)
в)
б) с "раздвижным" конусом и
эластичными элементами;
в) с фильтрующими сетками в разгрузочных камерах
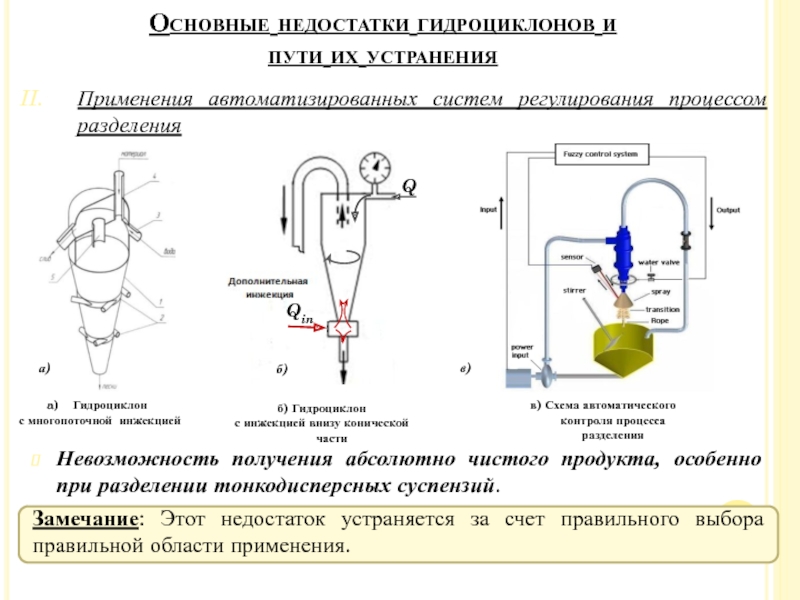
Слайд 43Применения автоматизированных систем регулирования процессом разделения
Невозможность получения абсолютно чистого продукта,
особенно при разделении тонкодисперсных суспензий.
Замечание: Этот недостаток устраняется за
счет правильного выбора правильной области применения.
Основные недостатки гидроциклонов и
пути их устранения
Гидроциклон
с многопоточной инжекцией
б) Гидроциклон
с инжекцией внизу конической части
в) Схема автоматического контроля процесса разделения
б)
в)
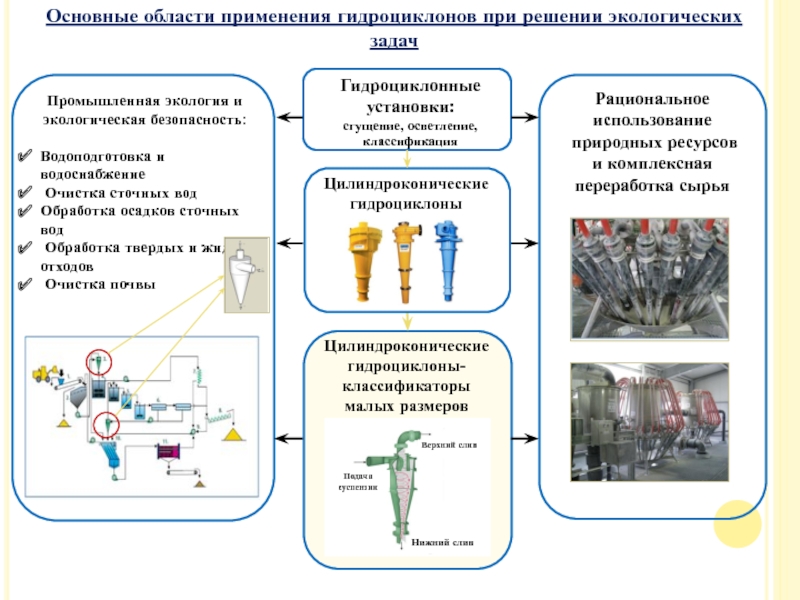
Слайд 44Основные области применения гидроциклонов при решении экологических задач
Цилиндроконические
гидроциклоны- классификаторы
малых размеров
Верхний слив
Нижний слив
Подача суспензии
Гидроциклонные установки:
сгущение, осветление, классификация
Рациональное
использование
природных
ресурсов
и комплексная
переработка сырья
Промышленная экология и
экологическая безопасность:
Водоподготовка и водоснабжение
Очистка сточных вод
Обработка осадков сточных вод
Обработка твердых и жидких отходов
Очистка почвы
Цилиндроконические гидроциклоны
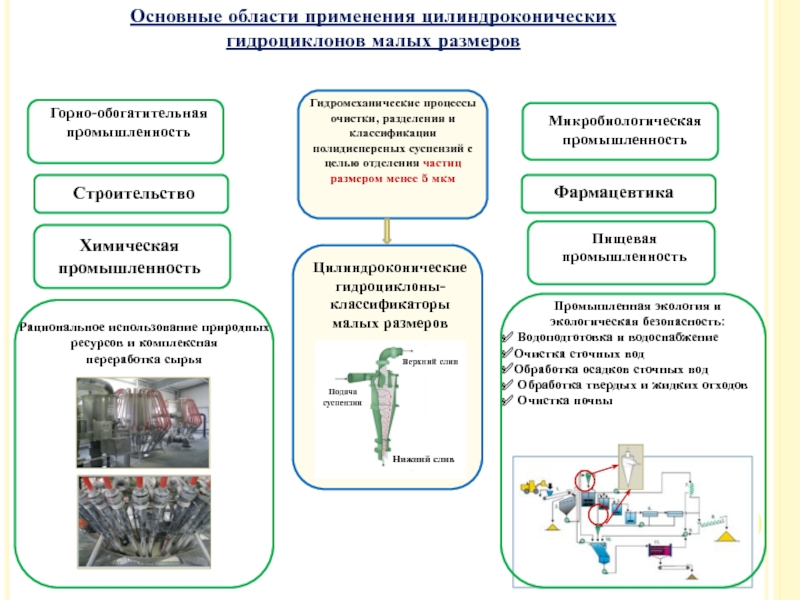
Слайд 45Основные области применения цилиндроконических
гидроциклонов малых размеров
Цилиндроконические
гидроциклоны- классификаторы
малых
размеров
Верхний слив
Нижний слив
Подача суспензии
Промышленная экология и
экологическая безопасность:
Водоподготовка и
водоснабжение
Очистка сточных вод
Обработка осадков сточных вод
Обработка твердых и жидких отходов
Очистка почвы
Рациональное использование природных ресурсов и комплексная
переработка сырья
Строительство
Фармацевтика
Микробиологическая
промышленность
Горно-обогатительная промышленность
Пищевая
промышленность
Химическая
промышленность
Гидромеханические процессы очистки, разделения и классификации полидисперсных суспензий с целью отделения частиц размером менее 5 мкм
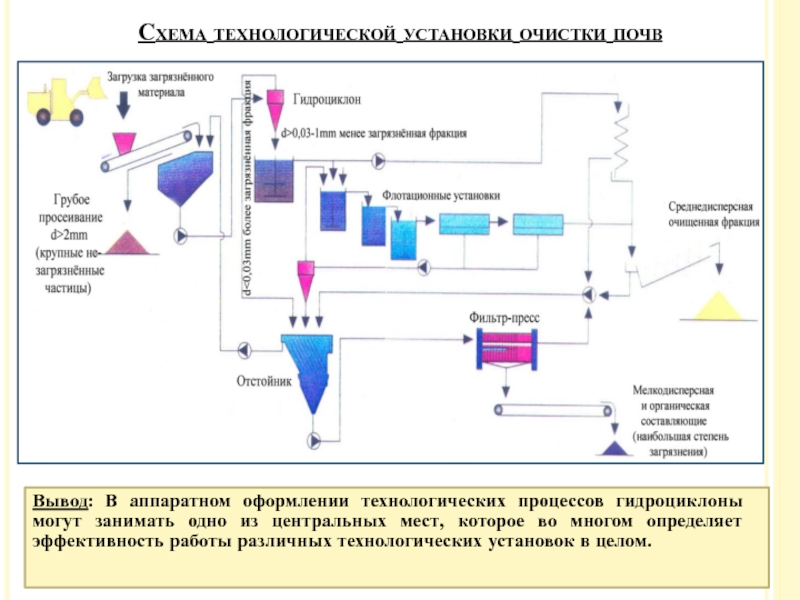
Слайд 46Схема технологической установки очистки почв
Вывод: В аппаратном оформлении технологических процессов
гидроциклоны могут занимать одно из центральных мест, которое во многом
определяет эффективность работы различных технологических установок в целом.
Слайд 47Принято выделять следующие методы расчета гидроциклонов:
Прямые методы - решают задачу
анализа, какие показатели разделения можно получить использую конкретную конструкцию циклона
с заданными геометрическими размерами при различных (заданных) давлениях питания дисперсной системы с известным составом и свойствами фаз.
Замечание: Данные методы подразумевают определение основных технологических показателей разделения, когда в качестве исходных данных заданы все физико-механические свойства разделяемой суспензии, известна функция распределения частиц дисперсной фазы по размерам, известен диаметр и все конструктивные размеры аппарата.
Вывод: К прямым методам относятся методы, базирующиеся на понятии граничного зерна включая графоаналитический метод, критериальные методы и стохастические методы.
Обратные методы - решают задачи синтеза, т.е. определения оптимальных геометрических размеров гидроциклонов и давления питания, необходимые для получения строго регламентированных показателей.
Вывод: К обратным методам относятся методы, определяющие унос твердой фазы, соотношение расходов, количество единиц оборудования и т.п.
Замечание: Поскольку при использовании обратных методов определяющих параметров достаточно много, задачи синтеза применительно к гидроциклонам обычно не имеют однозначного решения.
Лекция 6. Методы расчета гидроциклонов

Слайд 48Определяющие конструктивные параметры
цилиндроконических гидроциклонов
1 – цилиндрический корпус;
2 –
крышка;
3 – коническая часть аппарата;
4 – питающий (входной)
патрубок;
5 – верхний сливной патрубок для вывода мелкодисперсного продукта разделения;
6 – нижний сливной патрубок для выгрузки крупнодисперсного продукта разделения.
Схема цилиндроконического
гидроциклона
Примечание: Данные таблицы используется, в основном, для расчетов аппаратов с диаметром цилиндрической части от 20 мм до 500 мм
Вывод: Геометрия циклонов с тангенциальным входом определяется восьмью величинами. Семь относительных параметров определяют конфигурацию аппарата, и один параметр – диаметр цилиндрического корпуса определяет его размер.
Слайд 49Внимание! Можно выбрать и другие варианты геометрии, но при этом
следует иметь ввиду следующие указания:
Для того, чтобы предотвратить "короткое замыкание»
входного потока на выходную трубу высота входного канала должна быть меньше длины выходного канала:
Во избежание необоснованных потерь давления необходимо, чтобы
Для удержания кончика вихря в пределах конуса необходимо, чтобы общая длина гидроциклона превышала величину трех диаметров его цилиндрической части:
Для более эффективного удаления высокодисперсных загрязнений угол конуса должен находиться в пределах 5…8о ;
Максимальная эффективность работы гидроциклона обычно достигается при:
Замечание: Меньшее значение угла конусности соответствует режиму осветления: - диаметр воздушного столба
Большее значение угла конусности: соответствует режиму сгущения.
Обычно диаметр воздушного столба определяют в виде:
Определяющие конструктивные параметры
цилиндроконических гидроциклонов
Слайд 50Общая производительность гидроциклонов
Можно выделить несколько основных расчетных схем при выводе
зависимостей для определения значения Qобщ.
Гидроциклон рассматривается как местное сопротивление.
Значение Qобщ
рассчитывают на основе формулы истечения через водослив, образованной краями сливной трубки.
Производительность аппарата определяется по общей формуле истечения жидкости из затопленного отверстия.
Обработка экспериментальных данных по Qобщ с применением теории подобия и метода размерности.
Замечание: Выделяют несколько групп формул для расчета гидравлических характеристик гидроциклонов, которые отличаются друг от друга,
количеством входящих в них параметров;
трудоемкостью расчета;
точностью получаемых результатов.
Внимание! Большинство формул получены на основе результатов индивидуального эксперимента и, как правило, имеют один или несколько коэффициентов значение которых необходимо определять опытным путем, если рабочие параметры вновь проектируемого аппарата отличаются от изучаемого в этих экспериментах.
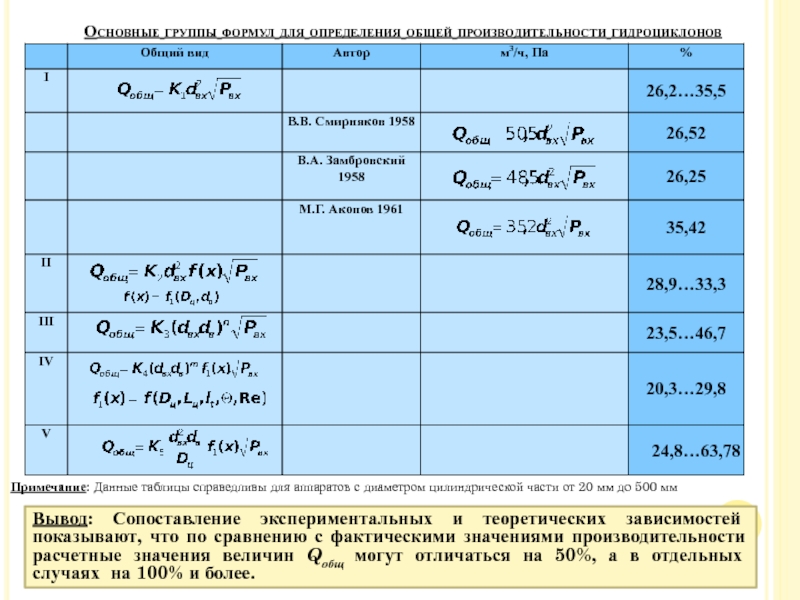
Слайд 51Вывод: Сопоставление экспериментальных и теоретических зависимостей показывают, что по сравнению
с фактическими значениями производительности расчетные значения величин Qобщ могут отличаться
на 50%, а в отдельных случаях на 100% и более.
Основные группы формул для определения общей производительности гидроциклонов
Примечание: Данные таблицы справедливы для аппаратов с диаметром цилиндрической части от 20 мм до 500 мм
Слайд 52Методика расчета основных размеров гидроциклона
Определяем расход в [дм3/мин] через
единичный гидроциклон:
При заданном давлении Рвх определяем сечение входного патрубка аппарата
в [см2]:
Эквивалентный диаметр входного отверстия находим по формуле:
Определяем диаметр цилиндрической части гидроциклона исходя из: в или
Замечание: При выполнении питающего отверстия прямоугольным отношение ширины отверстия a к его высоте b принимается (в зависимости от диаметра аппарата) равным:
далее определяются конкретные размеры из выражения: с учетом того, что а ≤ 5…10 δмах , где δмах – максимальный размер частиц.
Принимая угол наклона питания 3о…5о, остальные геометрические размеры определяют по известным пропорциям.
Внимание! Если размеры гидроциклона не соответствуют его функциональному назначению и особенностям технологического цикла (слишком большой диаметр, для разделения тонких суспензий) число единиц оборудования определяют исходя из выражений:
где n – отношение диаметров большого и малого циклона, m - число малых циклонов. Далее,
Слайд 53в периферийной части аппарата:
Лекция 7. Характеристики основных потоков
и структура дисперсионной среды в цилиндроконических гидроциклонах
Отвод мелкодисперсного
продукта классификации
Отвод крупнодисперсного
продукта классификации
4 зоны: 1 - нисходящий поток,
2 - восходящий поток, 3 - зона
циркуляции (20-30% объемной пропускной способности
гидроциклона),
4 - воздушный столб
Зависимость для определения тангенциальной скорости дисперсионной среды:
в центральной части аппарата :
Зависимость для определения радиальной скорости в периферийной части гидроциклона:
в известных методиках hрз= h= const;
Подвод
суспензии
Особенности осевой скорости потока:
в периферийной части
в центральной части
Особенности детерминированно-стохастической природы потоков:
Оценки величины интенсивности случайных составляющих процесса:
εφ εr - степени турбулентности потока в радиальном и окружном направлении
Слайд 54Уравнение движения
Теорема Кориолиса определяет силы инерции и описывает движение
частицы при ускоренном произвольном движении подвижной системы отсчета S относительно
неподвижной системы отсчета S1.
Это движение можно разложить на два:
поступательное движение со скоростью , равной скорости движения начала координат 0,
вращательное движение вокруг мгновенной оси, проходящей через это начало.
Замечание: Угловая скорость этого вращения может меняться как по модулю, так и по направлению. Единичные орты координатных осей системы S ортогональны, длины неизменны, но направление каждого из них с течением времени может изменяться (переменные векторы). При этом каждый из них может вращаться с угловой скоростью .
Тогда:
Слайд 55Уравнение движения
В первой скобке
- скорость
в системе отсчета S, во второй –
Таким образом
где
Эту величину равную абсолютной скорости покоящейся точки в движущейся системе отсчета S часто называют переносной скоростью или скоростью переноса.
Переносная скорость состоит из двух частей:
скорости движения начала координат 0;
скорости возникающей из-за вращения системы S вокруг этого начала.
Применительно к ускорениям по аналогии со скоростями имеем:
Далее и
Окончательно:
где и
Вывод: Теорема Кориолиса- абсолютное ускорение является векторной суммой относительного, кориолисова и переносного ускорения.
Слайд 56Если рассматривать криволинейное движение стоксовской сферической частицы массы mч и
диаметра dч в подвижной системе координат, то скорость частицы
где – скорость дисперсионной среды (потока), – относительная скорость движения частицы, а ее ускорение определяется теоремой Кориолиса в виде:
Вывод: Каждый член левой части уравнения представляет собой некоторый компонент силы, с которой частица действует на поток, стремящийся искривить траекторию частицы и изменить ее скорость. В правой части уравнения представлена гидродинамическая сила, действием которой объясняется указанный эффект, т.е. внешняя сила сопротивления, определяемая формулой Стокса.
Уравнение движения
где t – время, ρч и ρс – плотность частиц и среды соответственно, R – текущий радиус вращения (расстояние от оси аппарата), – угловая скорость вращения, µc – динамическая вязкость дисперсионной среды, Σ – прочие силы, включая случайные составляющие всех сил.
Слайд 57Первый член уравнения связан с ускорением классификационного движения и может
быть равен нулю при условии vс = const. Это возможно
только для практически безынерционных частиц, размеры которых не превышают 100 мкм. Для этих частиц, также можно считать пренебрежимо малыми величинами, составляющие силы сопротивления, обусловленные нестационарностью движения частиц, которые включены в состав сил Σ.
Второй член представляет собой центробежную силу (с учетом вытеснения частицей соответствующего объема дисперсионной среды), направленную по радиусу закругления потока.
Третий член уравнения выражает реакцию частицы, на тормозящее влияние среды при переходе частицы в более замедленные слои. Этот вектор по направлению всегда совпадает с . Для безынерционных частиц его можно исключить из рассмотрения.
Четвертый член представляет собой силу Кориолиса, которой также можно пренебречь, т.к. ωR >> dR/dt (скорость окружного движения много больше радиальной скорости частицы).
В пятый член, при необходимости, могут быть включены дополнительные силы, например, сила динамического сопротивления среды:
сила, учитывающая структурно-механические свойства разделяемой системы, обусловленные динамическим напряжением сдвига и т.п.
Уравнение движения

Слайд 58В результате для радиального движения частиц получаем:
где u’=u’(Q,R) – средняя
скорость радиального движения дисперсионной среды.
Для граничного зерна разделения δ
скорость u=0
по Тарьяну имеем:
где l – высота зоны сепарации, равная расстоянию между осью питающего патрубка и нижнего выходного отверстия.
В результате получаем:
крупнее в пески, мельче в слив.
Уравнение движения
Слайд 59Существует три основных определения понятия граничного зерна:
Граничным зерном δгр50 является
зерно узкого класса, содержание которого в сливе и песках составляет
50%.
Граничным зерном δгр является зерно узкого класса, такое что суммарное содержание зерен крупнее его в питании аппарата соответствует выходу песков.
Граничным зерном dгр является зерно узкого класса, содержание которого в сливе, песках и питании одинаково, а извлечение в слив и пески равно выходам этих продуктов.
Вероятностно-статистическая модель процесса классификации
При изучении изменения гранулометрического состава примесей в технологических процессах, ограничимся рассмотрением унарной функции fп = N f, зависящей от пространственных переменных {R}, характерного размера частиц {δ} и времени t.
Будем нормировать fп таким образом, что
fп ({R},{δ}, t) d{δ} = n ({R}, t); n ({R}, t) d{R} = N (t) (1.1)
где n({R}, t) - плотность распределения частиц в пространстве системы (штучная концентрация частиц в системе); N (t) - полное число частиц.
Граничное зерно разделения
Слайд 60Основные характеристик разделения цилиндроконических гидроциклонов-классификаторов малых размеров с инжекцией
Эффективность
улавливания частиц всех фракций в нижнем сливе гидроциклона:
Эффективность извлечения частиц
все фракций в верхний слив гидроциклона:
Эффективность разделения высокодисперсных частиц i-ой фракции в гидроциклоне:
Эффективность разделения частиц i-ой фракции в гидроциклоне:
масса частиц всех фракций на входе в гидроциклон, в нижнем и верхнем сливах аппарата соответственно ;
расход суспензии на входе в гидроциклон, в нижнем и верхнем сливах аппарата соответственно ;
концентрация суспензии на входе в гидроциклон, в нижнем и верхнем сливах аппарата соответственно ;
время отбора суспензии на входе в гидроциклон, в нижнем и верхнем сливах аппарата соответственно ;
сплит-параметр, показывает распределение основного потока между выходными патрубками.
Считается, что , тогда
масса частиц i-ой фракции на входе в гидроциклон и в нижнем сливе аппарата.
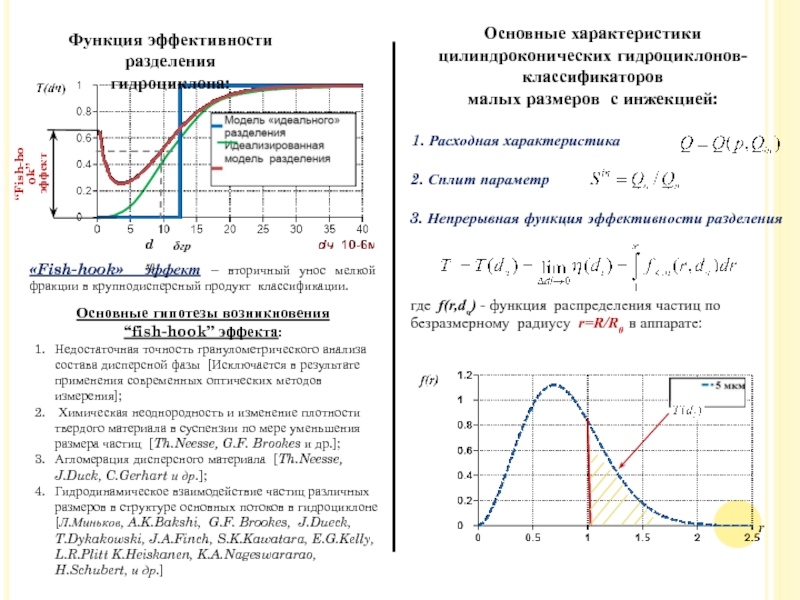
Функция эффективности
разделения частиц
всех фракций:
Слайд 61«Fish-hook» эффект – вторичный унос мелкой фракции в крупнодисперсный продукт
классификации.
d50
“Fish-hook” эффект
δгр
Основные гипотезы возникновения
“fish-hook” эффекта:
Недостаточная точность гранулометрического анализа состава
дисперсной фазы [Исключается в результате применения современных оптических методов измерения];
Химическая неоднородность и изменение плотности твердого материала в суспензии по мере уменьшения размера частиц [Th.Neesse, G.F. Brookes и др.];
Агломерация дисперсного материала [Th.Neesse, J.Duck, C.Gerhart и др.];
Гидродинамическое взаимодействие частиц различных размеров в структуре основных потоков в гидроциклоне [Л.Миньков, A.K.Bakshi, G.F. Brookes, J.Dueck, T.Dykakowski, J.A.Finch, S.K.Kawatara, E.G.Kelly, L.R.Plitt K.Heiskanen, K.A.Nageswararao, H.Schubert, и др.]
где f(r,dч) - функция распределения частиц по
безразмерному радиусу r=R/R0 в аппарате:
Основные характеристики цилиндроконических гидроциклонов-классификаторов
малых размеров с инжекцией:
1. Расходная характеристика
2. Сплит параметр
3. Непрерывная функция эффективности разделения
Функция эффективности разделения
гидроциклона:
Слайд 62Тогда функция:
f ({R},{δ}, t) d{δ}d{R} = fп ({R},{δ}, t) d{δ}d{R}/
N (t)
(1.2)
будет характеризовать вероятность попадания произвольной частицы с размером в интервале от {δ} до {δ}+d{δ} в момент времени t в достаточно малый объем d{R} с постоянным содержанием дисперсной фазы, в котором расположена точка с координатами {R}. В результате имеем:
f ({R},{δ}, t) d{δ} = n0 ({R}, t); n0 ({R}, t) d{R} = 1 (1.3)
где n0 ({R}, t) - плотность распределения вероятности в пространстве системы (относительная штучная концентрация частиц в системе);
Функции fп ({R},{δ},t) и f ({R},{δ},t) являются функциями плотности распределения вероятности в фазном пространстве ({R},{δ}) в момент времени t. При этом согласно (1.1) и (1.2.) fп ({R},{δ}, t) - нормирована на число частиц в системе, а f ({R},{δ}, t) – на единицу.
Кроме того, можно записать:
fп ({R},{δ}, t) d{R} = fпΣ ({δ}, t); fпΣ ({δ}, t) d{δ} = N (t) (1.4)
f ({R},{δ}, t) d{R} = fΣ ({δ}, t); fΣ ({δ}, t) d{δ} = 1 (1.5)
где fпΣ ({δ}, t) и fΣ ({δ}, t) - плотности распределения всех частиц по размерам в системе, нормированные соответственно на число частиц в системе и на единицу.
Вероятностно-статистическая модель процесса классификации

Слайд 63По определению условной плотности распределения одной из случайных величин, входящих
в систему ? можно записать:
fп ({R}, {δ}, t) = n
({R}, t) fпΣ ({δ}{R0}, t) = fпΣ ({δ}, t) n ({R}{δ0}, t) (1.6)
f ({R},{δ}, t) = n0 ({R}, t) fΣ ({δ}{R0}, t) = fΣ ({δ}, t) n0 ({R}{δ0}, t) (1.7)
где fпΣ ({δ}{R}, t) и fΣ ({δ}{R}, t) – условные плотности распределения частиц по размерам {δ} в точке с координатой {R0}, т.е. при условии, что случайная величина {R} приняла значение {R0}; n ({R}{δ0}, t) и n0 ({R}{δ0}, t) – условная плотность распределения концентрации частиц с размером {δ0} в пространстве {R}, т.е. при условии, что случайная величина {δ} приняла значение {δ0}.
Внимание! Корректное описание происходящих в системе процессов возможно только на основании кинетических уравнений отражающих изменение гранулометрического состава примесей в технологических процессах, т.е. в пространстве и во времени. Выбор же определяющих параметров зависит от стоящих перед разработчиком задач.
Вероятностно-статистическая модель процесса классификации
Слайд 64Для описания изменения гранулометрического состава примесей нас в большей мере
будет интересовать функция f ({R},{δ}, t).
В результате, поставленная задача
может быть сведена к парному отысканию функций n0 ({R}, t) и fΣ ({δ}{R0}, t) или fΣ ({δ}, t) и n0 ({R}{δ0}, t).
Для упрощения изложения будем считать, что каждый из аргументов {R} и {δ} полностью характеризоваться только одним параметром. Другими словами, мы будем анализировать изменение искомых функций не более чем в двухмерном пространстве случайных величин R и δ.
Обозначим через D+(δ-δ) некоторый параметр, определяющий интенсивность случайного перехода частиц из класса с характерным размером (δ-δ) в класс с характерным размером (δ) за единицу времени.
Аналогично, обозначим через D-(δ) - некоторый параметр, определяющий интенсивность случайного перехода частицы из класса с характерным размером (δ) в класс с характерным размером (δ-δ).
Тогда, для нестационарного состояния, правая часть выражения:
J (δ, t) = fΣ (δ-δ, t) D+(δ-δ) - fΣ (δ, t) D-(δ) (1.8)
будет характеризовать избыток или недостаток доли частиц, которые в единицу времени переходят из класса (δ-δ) в класс δ, над долей частиц, которые в то же самое время переходят из класса δ в класс(δ-δ).
Вероятностно-статистическая модель процесса классификации

Слайд 65Для нахождения кинетического уравнения функции fΣ (δ, t) введем в
рассмотрение функцию ее стационарного распределения fсΣ (δ). При этом будем
считать, что система может достигнуть стационарного состояния, при котором доля частиц любого размера остается постоянной.
Тогда, взаимосвязь между D+(δ-δ) и D-(δ) получим из условия:
fсΣ (δ-δ) D+(δ-δ) = fсΣ (δ) D-(δ) или
D+(δ-δ) = fсΣ (δ) D-(δ)/ fсΣ (δ-δ) (1.9)
Подставляя (1.9) в выражение (1.8) получаем:
J (δ, t) = fсΣ (δ) D-(δ) [fΣ (δ-δ, t)/ fсΣ (δ-δ) – fΣ (δ, t)/ fсΣ (δ)] (1.10)
Считая, что при любых значениях δ, δ по сравнению с δ, – весьма малая величина, J (δ, t) в (1.10) можно трактовать как функцию непрерывного аргумента δ.
В результате имеем:
J (δ, t) = - fсΣ (δ) D-(δ) ∂ [ fΣ (δ, t)/ fсΣ (δ)]/ ∂δ (1.11)
Полагая, D-(δ) = D(δ) получим:
J (δ, t) = - D(δ) ∂fΣ (δ, t)/ ∂δ + D(δ) fΣ (δ, t) ∂ ln fсΣ (δ)/ ∂ δ (1.12)
Вероятностно-статистическая модель процесса классификации
Слайд 66Если принять ln fсΣ (δ) = const - kU(δ), то
выражение (1.12) формально становится тождественным известному уравнению для потока частиц
с плотностью fΣ (δ, t), вызванного с одной стороны, диффузией, а с другой – действием некоторой внешней силы F, соответствующей потенциальной энергии - U(δ), т.е. можно записать:
J (δ, t) = - D(δ) ∂ fΣ (δ, t)/ ∂δ - k D(δ) fΣ (δ, t) dU(δ)/dδ (1.13)
Тогда скорость изменения - ∂fΣ (δ, t)/ ∂t можно определить следующим образом:
∂fΣ (δ, t)/ ∂t = J (δ, t) - J (δ+δ , t) = - ∂J (δ, t)/ ∂δ (1.14)
В результате, из совместного рассмотрения (1.13) и (1.14) получаем искомое кинетическое уравнение рассматриваемого процесса:
∂fΣ (δ,t)/ ∂t = k∂[D(δ) fΣ (δ,t) dU(δ)/dδ]/∂δ + ∂[D(δ) ∂fΣ (δ,t)/∂δ]/∂δ (1.15)
Уравнение (1.15) совпадает с известным уравнением Фоккера – Планка при условии:
wΣ(δ) = k D(δ) dU(δ)/dδ (1.16)
где wΣ (δ) = dδ/dt - средняя скорость систематического изменения величины δ.
Вероятностно-статистическая модель процесса классификации
Слайд 67Тогда кинетическое уравнение (1.15) для функции fΣ (δ, t), полученное
исходя из вероятностных предпосылок, позволяет рассматривать процесс изменения гранулометрического состава
всей совокупности частиц как некоторый случайный марковский процесс вхождения в рассматриваемую систему и выхода из нее.
Стационарное распределение fсΣ (δ) может быть получено из (1.15) при условии:
∂fΣ (δ, t)/ ∂t = - ∂J(δ, t)/ ∂δ = 0,
которое выполняется при J (δ, t) = const. С учетом принятого раннее допущения о постоянстве доли частиц любого размера получаем:
J (δ, t) = - D(δ) ∂fΣ (δ, t)/ ∂δ - k D(δ) fΣ (δ, t) dU(δ)/dδ = 0 или
d fсΣ (δ)/dδ = - k fсΣ (δ) dU(δ)/dδ
После интегрирования, с учетом (1.5) получаем:
fсΣ (δ) = k exp ( - k U(δ)) (1.17)
Вывод: Функция fсΣ (δ), определяется энергией системы U(δ).
Вероятностно-статистическая модель процесса классификации
Слайд 68При этом, используя принцип максимума энтропии и считая, равновесные и
стационарные состояния совпадающими между собой можно утверждать, что распределение (1.17)
соответствует такой системе, где помимо ограничения (1.15) существует еще одно:
U(δ) fсΣ (δ) dδ = Uср(δ) (1.18)
где Uср(δ) – средняя энергия рассматриваемой системы.
Замечание: Мы пришли к каноническому распределению закрытой макросистемы показывающему, что никаких ограничений на вид функции fсΣ (δ), кроме условия нормировки и фиксированности среднего значения энергии системы не существует. При этом элементы системы будут находиться в наиболее вероятном состоянии, соответствующем распределению (1.17).
Стохастическая природа происходящих процессов проявляется в наличии флуктуаций скорости изменения какого-либо параметра системы. При этом флуктуации происходят около среднего значения, что в свою очередь приводит к флуктуациям функции плотности распределения.
Указанное обстоятельство позволяет представить величину скорости wп(R) для функции n0 (Rδ0, t) в виде:
wп(R) = wп(R) + wпф(R) (1.18)
где wп(R) = dR/dt - средняя скорость систематического изменения величины R, а wпф(R) – флуктуационная составляющая скорости wп(R).
Вероятностно-статистическая модель процесса классификации

Слайд 69Соответственно имеем:
n0 (Rδ0, t) = n0 (Rδ0, t) + n0
ф (Rδ0, t)
(1.19)
где n0 (Rδ0, t) - средняя плотность концентрации, а n0 ф (Rδ0, t) – флуктуационная составляющая n0 (Rδ0, t).
Принимая wп(R) n0 (Rδ0, t) = J (R, t), по аналогии с (1.14) можно записать:
∂n0 (Rδ0,t)/∂t = J(R,t) - J (R+R,t) = - ∂J(R,t)/∂R = -∂[Jwп(R) n0 Rδ0,t)]/ ∂R (1.20)
В результате, с учетом (1.18)…(1.20) получаем:
∂[n0 (Rδ0, t) + n0 ф (Rδ0, t)]/ ∂t =
- ∂[wп(R) n0 (Rδ0, t) + wп(R) n0 ф (Rδ0, t) + n0 (Rδ0, t) wпф(R) + n0 ф (Rδ0, t) wпф(R)]/ ∂R
Проводя осреднение за конечный промежуток времени, с учетом:
wпф(R) = n0 ф (Rδ0, t) = 0, можно записать:
∂[n0 (Rδ0, t)]/ ∂t = - ∂[wп(R) n0 (Rδ0, t) + n0 ф (Rδ0,t) wпф(R)]/∂R (1.21)
Вероятностно-статистическая модель процесса классификации
Слайд 70В уравнении (1.21) величина n0 ф (Rδ0, t) wпф(R) отлична
от нуля из-за наличия нелинейности между флуктуационными составляющими.
Если n0 ф
(Rδ0, t) wпф(R) представить как:
n0 ф (Rδ0, t) wпф(R) = - ∂[ D(R) n0 (Rδ0, t)]/ ∂R
то окончательно получаем:
∂n0 (Rδ0,t)/∂t = -∂[wп(R) n0 (Rδ0,t)]/ ∂R + ∂2[D(R) n0 (Rδ0,t)]/ ∂R2 (1.22)
Мы пришли к частному случаю уравнения (уравнение ФПК), где D(R) – коэффициент диффузии на прямой параметра R. При этом уравнение (1.15) после элементарных преобразований может быть приведено к виду (1.22).
Вывод: В результате мы получили необходимые кинетические уравнения в виде (1.15) и (1.22). При этом мы считали, что частицы дисперсной фазы не оказывают друг на друга взаимного влияния. Подобное допущение позволяет распространить полученные результаты только на малоконцентрированные дисперсные системы.
Вероятностно-статистическая модель процесса классификации
Слайд 71Уравнения (1.15) и (1.22) при наличии граничных и начальных условий
могут быть решены численными методами, более того во многих случаях
они допускают аналитические решения на основе задачи Штурма – Лиувилля, методом разделения переменных.
Однако, мы ограничимся рассмотрением случаев когда:
∂fΣ (δ, t)/ ∂t = ∂n0 (Rδ0, t)/ ∂t = 0
Физически это означает, что состояние системы соответствует установившемуся движению, которое достигается после затухания всех переходных процессов, связанных с влиянием начальных условий.
Замечание: Разумеется, стационарные функции распределения могут существовать лишь при условии постоянства во времени параметров системы и стационарных, случайных возмущений, но эти условия в общем случае еще не являются достаточными.
Вывод: Обратимся к рассмотрению асимптотических свойств модели при t ∞ и одновременно сопоставим полученные результаты с известными аппроксимационными функциями распределения, применяемыми для описания гранулометрического состава примесей.
Вероятностно-статистическая модель процесса классификации






































![ГИДРОЦИКЛОНИРОВАНИЕ Методика расчета основных размеров гидроциклона Определяем расход в [дм3/мин] через единичный Методика расчета основных размеров гидроциклона Определяем расход в [дм3/мин] через единичный гидроциклон:При заданном давлении Рвх определяем сечение](/img/thumbs/da8763378361dfb4d1944d1044541868-800x.jpg)






































