Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ГЛАВА I. МЕХАНИКА § 8. Работа и энергия
Содержание
- 1. ГЛАВА I. МЕХАНИКА § 8. Работа и энергия
- 2. I. Кинетическая энергияКинетическая энергия — энергетическая характеристика
- 3. §8. Работа и энергия Доказательство4. Кинетическая энергия
- 4. §8. Работа и энергия ДоказательствоРазобьём тело на
- 5. §8. Работа и энергия II. Работа и
- 6. 3. Работа при вращательном движении ТТ4. МощностьМощность
- 7. — скорость точки приложения силыIII. Теорема об
- 8. Теперь рассмотрим механическую систему. Для i-ой материальной
- 9. ДоказательствоПо определению потенциального поляИзменением потенциальной энергии МТ
- 10. Примеры расчёта работы и потенциальной энергии1. Работа
- 11. При Wп(0) = 03. Работа силы тяжестиСила тяжести потенциальна.При
- 12. Центральная сила потенциальна.Частный случайГравитационное полеПри Wп(∞) = 0V. Связь
- 13. В декартовой системе координат— частная производная функции
- 14. ПримерДана зависимость потенциальной энергии МТ в некотором
- 15. ПримерПотенциальная энергия системы двух гравитирующих телДва тела
- 16. Закон изменения механической энергии: изменение механической энергии
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ГЛАВА I. МЕХАНИКА
§8. Работа и энергия
О. И. Лубенченко
НИУ МЭИ
Кафедра физики
им. В. А. Фабриканта
Слайд 2I. Кинетическая энергия
Кинетическая энергия — энергетическая характеристика движения.
[Wк] = Дж
(джоуль).
1. Кинетическая энергия МТ:
2. Кинетическая энергия механической системы:
Кинетическая энергия тела,
совершающего поступательное движение:(m — масса тела, v — модуль его скорости)
3. Кинетическая энергия ТТ, вращающегося вокруг неподвижной оси:
§8. Работа и энергия
Слайд 3§8. Работа и энергия
Доказательство
4. Кинетическая энергия ТТ, совершающего плоское движение
Теорема
Кёнига: кинетическая энергия ТТ, совершающего плоское движение, равна сумме кинетической
энергии поступательного движения этого тела со скоростью, равной скорости Цм тела, и вращения тела вокруг оси, проходящей через ЦМ тела перпендикулярно плоскости движения:Слайд 4§8. Работа и энергия
Доказательство
Разобьём тело на малые фрагменты массой Δmi.
Вычислим кинетическую энергию тела по определению:
Слайд 5§8. Работа и энергия
II. Работа и мощность
Работа — скалярная ФВ
— энергетическая характеристика взаимодействия.
[A] = Дж
1. Элементарная работа:
2. Работа:
l —
траектория точки приложения силы Графический смысл работы: площадь под кривой Fl(l) равна модулю работы при перемещении точки приложения этой силы по траектории l.
Слайд 63. Работа при вращательном движении ТТ
4. Мощность
Мощность — скалярная ФВ
— энергетическая характеристика взаимодействия (или тела, совершающего работу), равная скорости
совершения работы.[N] = Вт (ватт)
Средняя мощность:
Мгновенная мощность:
§8. Работа и энергия
Слайд 7— скорость точки приложения силы
III. Теорема об изменении кинетической энергии
Изменение
кинетической энергии механической системы равно сумме работ внешних и внутренних
сил:Доказательство
Рассмотрим МТ массы m, которая испытывает воздействие, описываемое силой
§8. Работа и энергия
Слайд 8Теперь рассмотрим механическую систему. Для i-ой материальной точки
IV. Потенциальная энергия
материальной точки
Поле (в математике) — величина как функция радиуса-вектора (или
координат). Задать силу как функцию радиуса-вектора материальной точки, воздействие на которую описывается этой силой, значит задать силовое поле.Поле в физике — физический объект.
Поле потенциально (сила потенциальна), если работа поля при перемещении МТ по любой замкнутой траектории равна нулю (иначе говоря, циркуляция силы по произвольному замкнутому контуру равна нулю):
Работа потенциального поля по перемещению МТ не зависит от формы её траектории, а зависит только от начального и конечного положения МТ.
§8. Работа и энергия
Слайд 9Доказательство
По определению потенциального поля
Изменением потенциальной энергии МТ при перемещении МТ
из положения 1 в положение 2 называется работа потенциального поля,
совершаемая при этом перемещении, взятая с обратным знаком:Потенциальная энергия МТ — ФВ — энергетическая характеристика взаимодействия, равная работе потенциального поля по перемещению МТ в данное положение из точки, где потенциальная энергия принята равной нулю, взятая с обратным знаком:
Потенциальная энергия определяется с точностью до произвольной постоянной.
§8. Работа и энергия
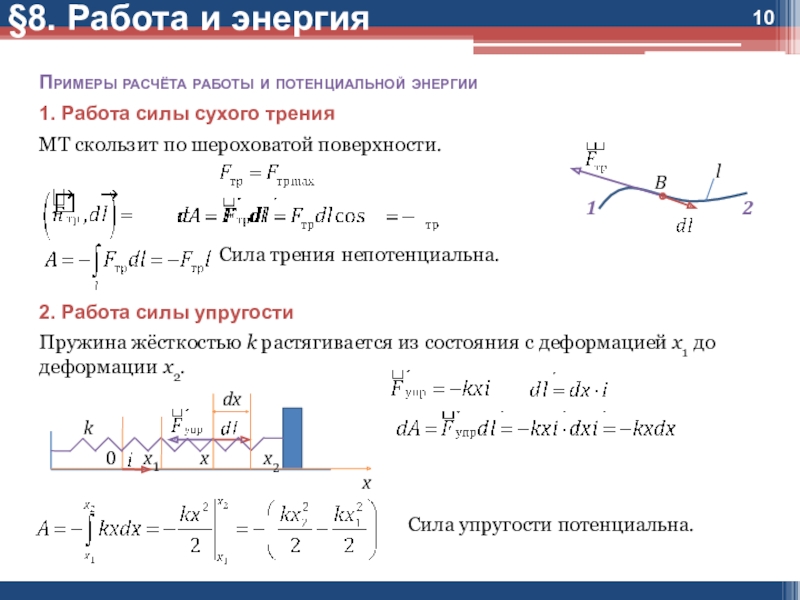
Слайд 10Примеры расчёта работы и потенциальной энергии
1. Работа силы сухого трения
МТ
скользит по шероховатой поверхности.
Сила трения непотенциальна.
2. Работа силы упругости
Пружина жёсткостью
k растягивается из состояния с деформацией x1 до деформации x2.Сила упругости потенциальна.
§8. Работа и энергия
Слайд 11
При Wп(0) = 0
3. Работа силы тяжести
Сила тяжести потенциальна.
При Wп = 0 при h = 0
4.
Поле центральных сил
Центральная сила — сила, модуль которой зависит только
от расстояния от точки, называемой силовым центром (центром силы), направленная вдоль радиуса-вектора, соединяющего центр силы с точкой приложения силы:§8. Работа и энергия
Слайд 12
Центральная сила потенциальна.
Частный случай
Гравитационное поле
При Wп(∞) = 0
V. Связь силы и потенциальной
энергии. Градиент
— оператор «набла» (оператор векторного дифференцирования)
§8. Работа и энергия
Слайд 13
В декартовой системе координат
— частная производная функции трёх переменных (x,
y, z) по x и т. д.
Градиент — произведение вектора ∇
на скалярную функцию — векторная функция скалярного аргумента; в декартовых координатахНаправление градиента — направление наиболее быстрого возрастания скалярной функции.
grad Wп = 0 — положение равновесия
Устойчивое равновесие — min Wп
Неустойчивое равновесие — max Wп
§8. Работа и энергия
Слайд 14Пример
Дана зависимость потенциальной энергии МТ в некотором поле от декартовых
координат: Wп = axyz, где a — постоянная. Найти силу, с которой
поле действует на МТ, как функцию координат.в любой точке на осях x, y, z — устойчивое равновесие при a > 0 и неустойчивое при a < 0.
VI. Потенциальная энергия механической системы
Потенциальная энергия механической системы равна работе внешних и внутренних потенциальных сил при переходе системы из данной конфигурации в конфигурацию, где потенциальная энергия системы принята равной нулю (конфигурация системы — это совокупность координат тел (МТ), входящих в эту систему):
§8. Работа и энергия
Слайд 15Пример
Потенциальная энергия системы двух гравитирующих тел
Два тела массами M и
m взаимодействуют гравитационно. Расстояние между центрами масс этих тел равно
r. Найти потенциальную энергию системы.Положим Wп(∞) = 0.
VII. Закон сохранения и изменения механической энергии
Рассмотрим механическую систему. По т. об изменении кинетической энергии
Механическая энергия системы — ФВ — сумма кинетической и потенциальной энергии:
§8. Работа и энергия
Слайд 16Закон изменения механической энергии: изменение механической энергии системы равно сумме
работ внешних и внутренних непотенциальных сил:
Закон сохранения механической энергии: механическая
энергия системы не изменяется с течением времени, если сумма работ внешних и внутренних непотенциальных сил равна нулю, а все внешние потенциальные силы стационарны (т. е. не зависят явным образом от времени).Консервативные силы — потенциальные силы и непотенциальные силы, работа которых равна нулю.
Диссипативные силы — непотенциальные силы, работа которых меньше нуля.
Диссипация энергии — переход энергии упорядоченных процессов (в данном случае —механической энергии) в энергию неупорядоченных процессов (внутреннюю энергию).
§8. Работа и энергия

![ГЛАВА I. МЕХАНИКА § 8. Работа и энергия I. Кинетическая энергияКинетическая энергия — энергетическая характеристика движения.[Wк] = Дж (джоуль).1. I. Кинетическая энергияКинетическая энергия — энергетическая характеристика движения.[Wк] = Дж (джоуль).1. Кинетическая энергия МТ:2. Кинетическая энергия механической](/img/tmb/7/624744/f914fe58b70275a0b017eedf857a4601-800x.jpg)


![ГЛАВА I. МЕХАНИКА § 8. Работа и энергия §8. Работа и энергия II. Работа и мощностьРабота — скалярная ФВ §8. Работа и энергия II. Работа и мощностьРабота — скалярная ФВ — энергетическая характеристика взаимодействия.[A] = Дж1.](/img/tmb/7/624744/4a33a21e9656a46d13c11ef5b7c5b4d8-800x.jpg)