Графическая иллюстрация свойств дискретного преобразования Фурье

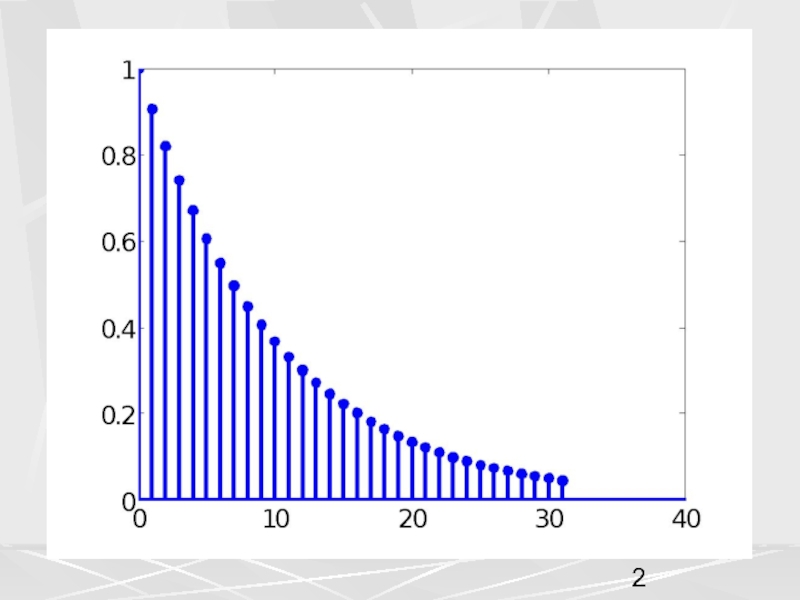
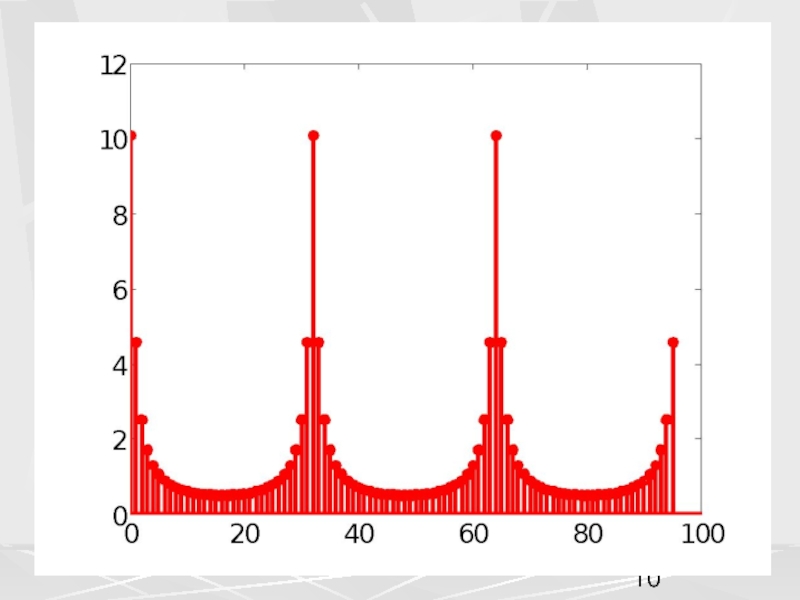
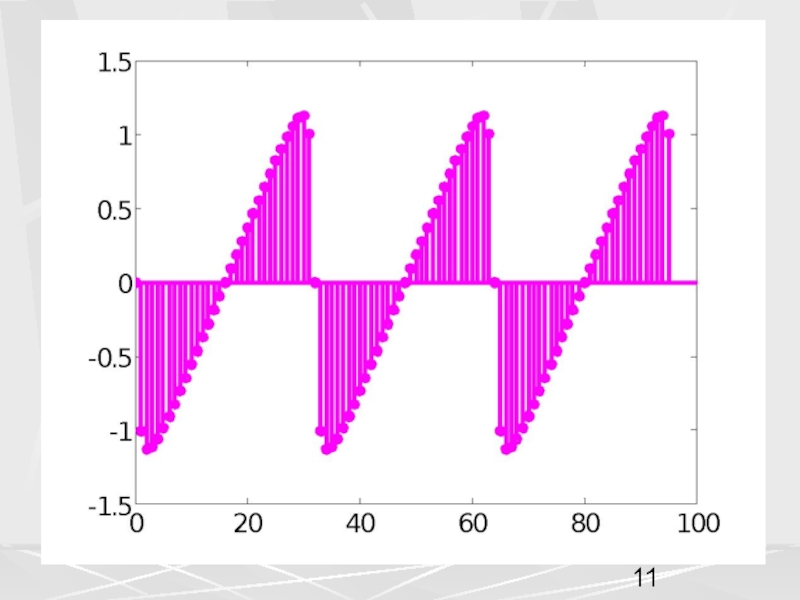
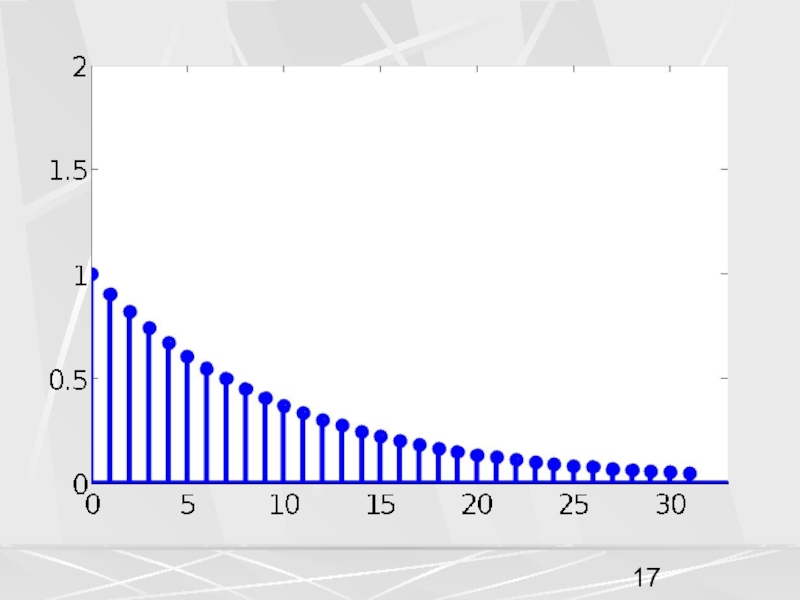
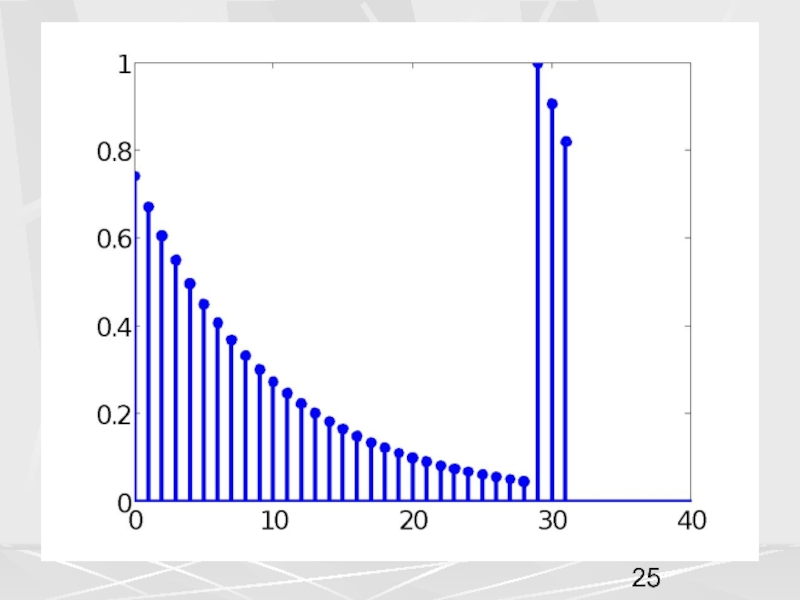
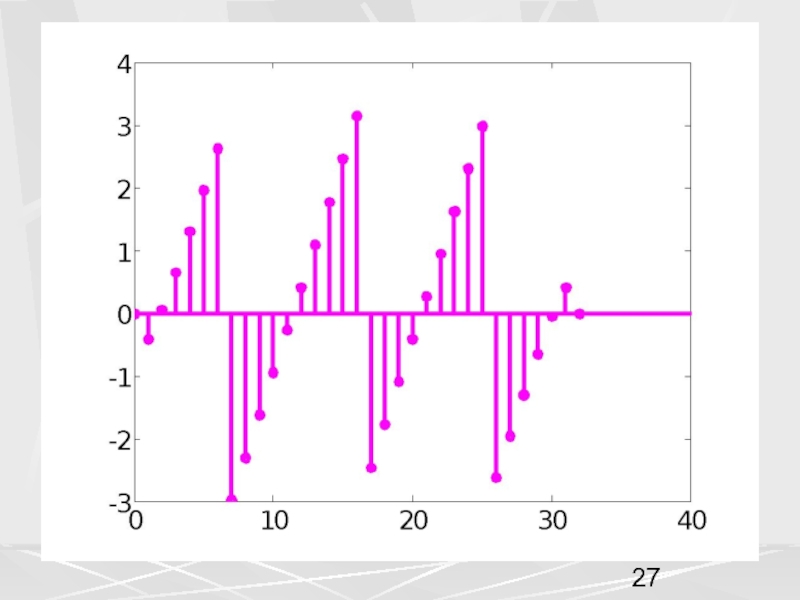
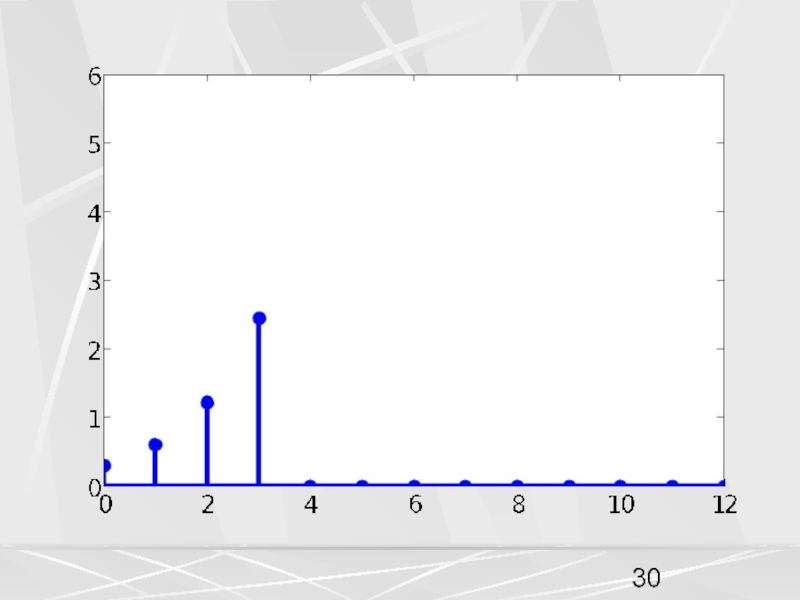
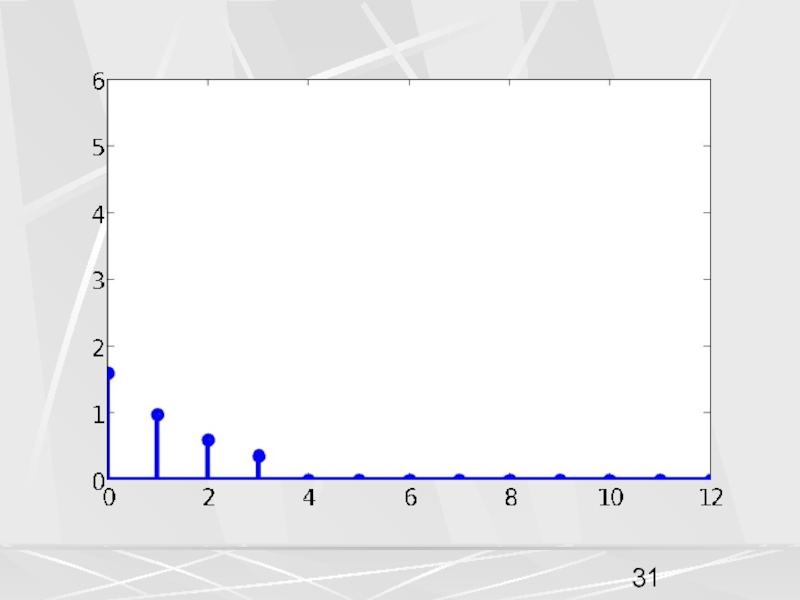
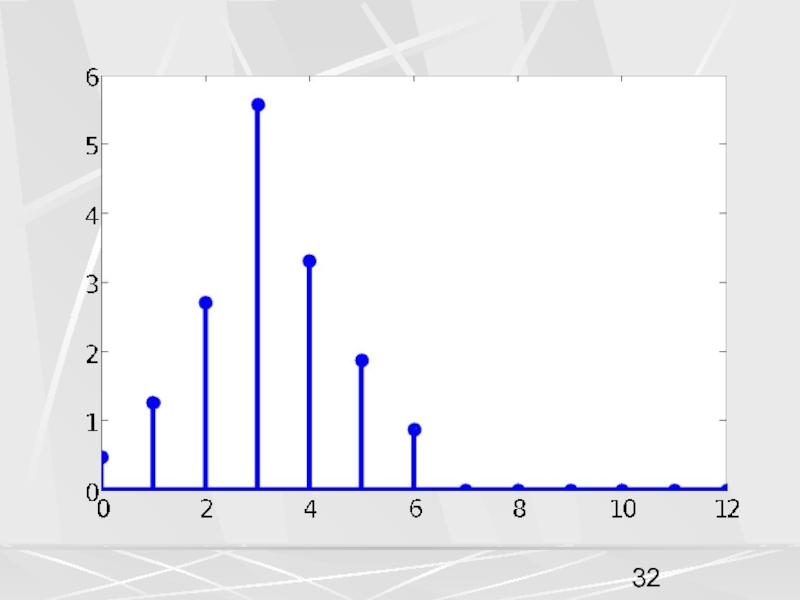
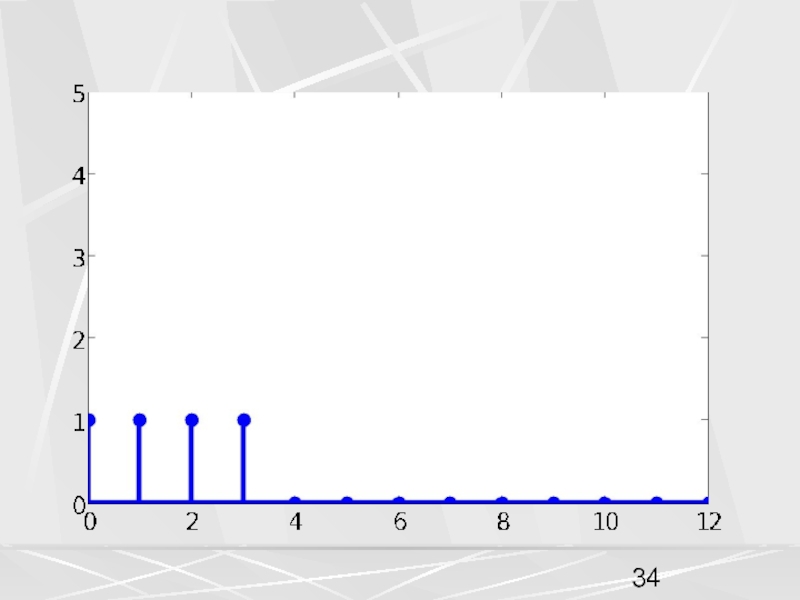
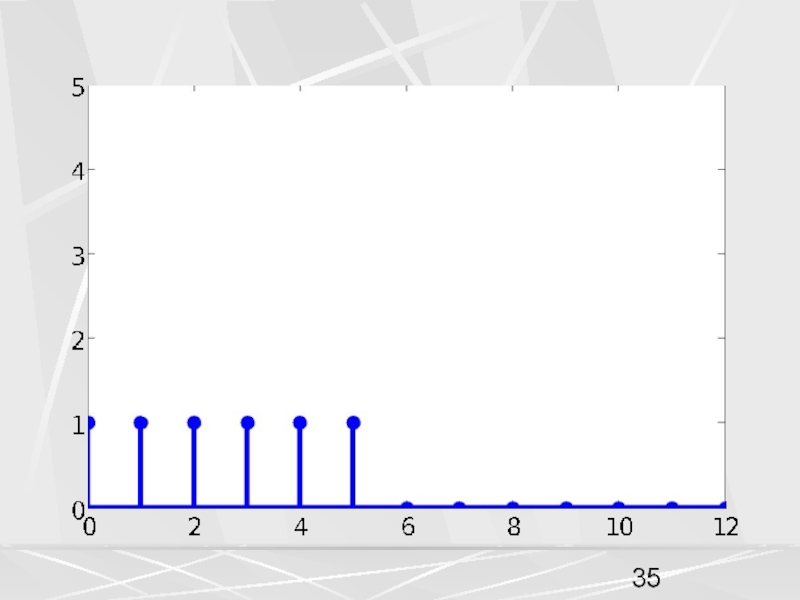
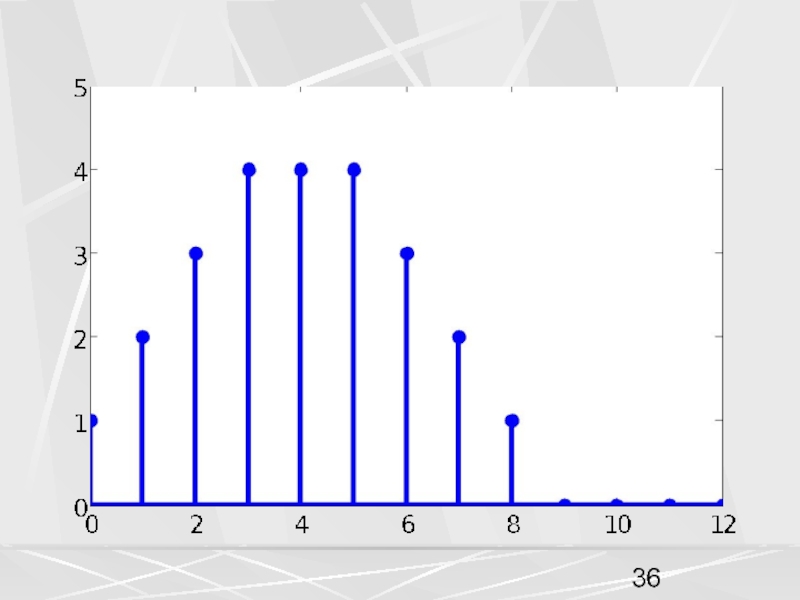
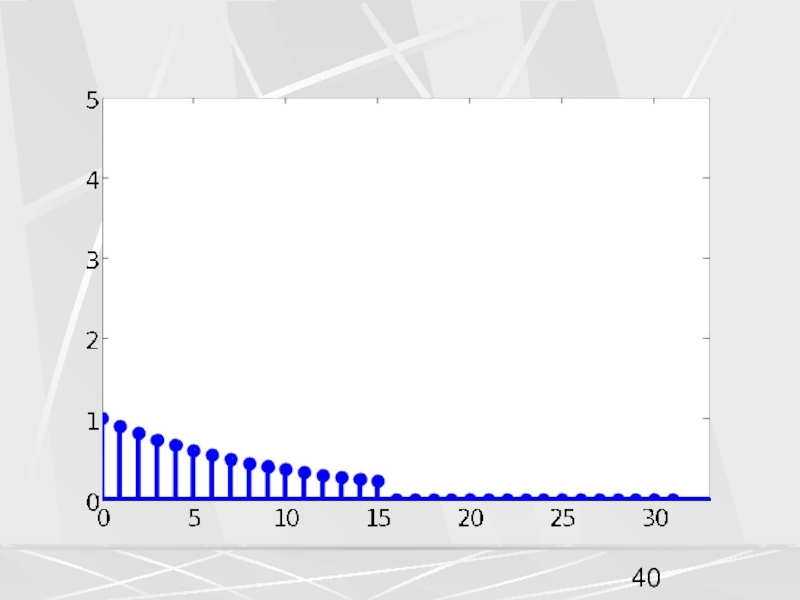
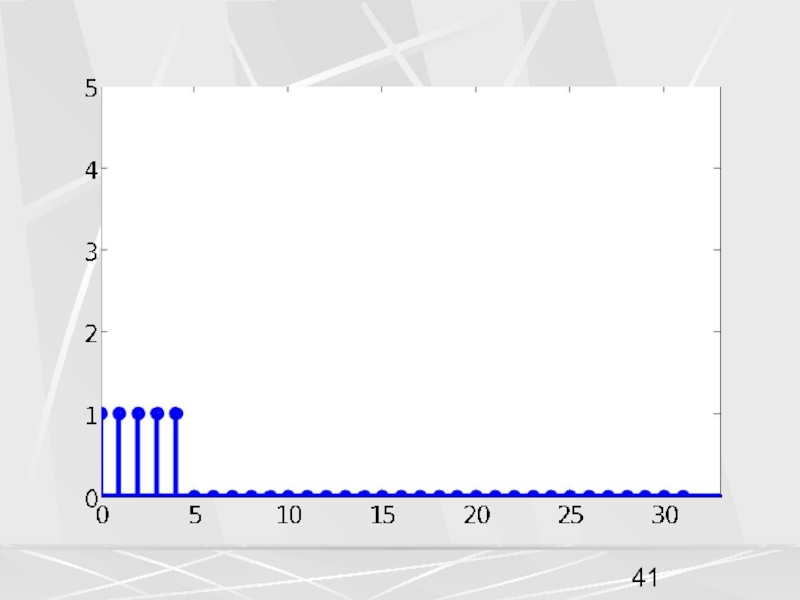
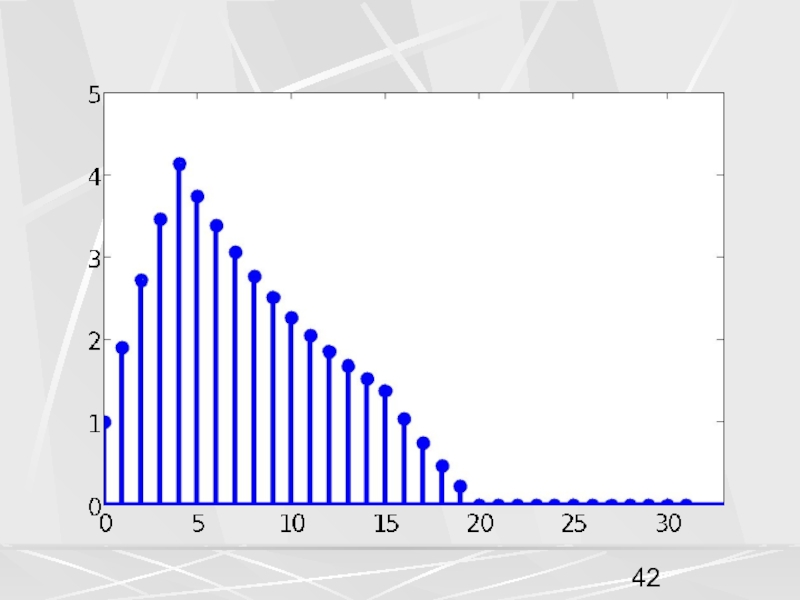
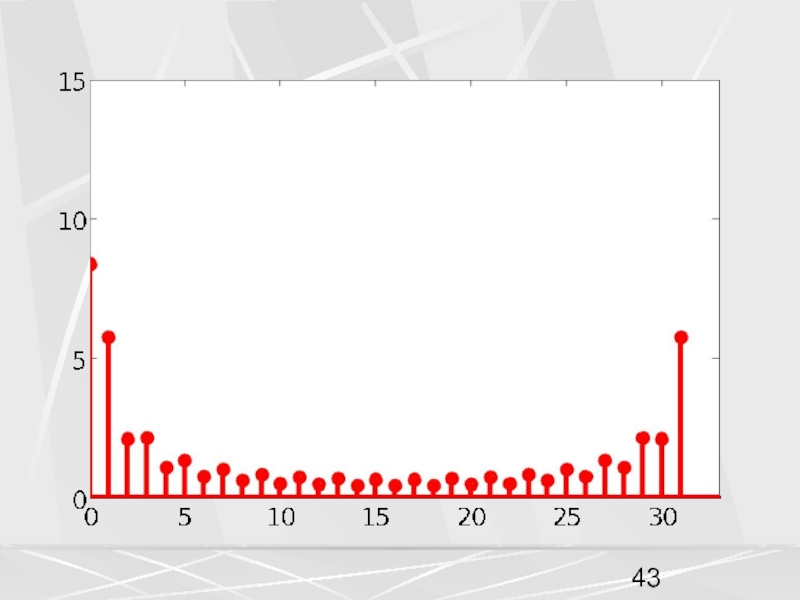
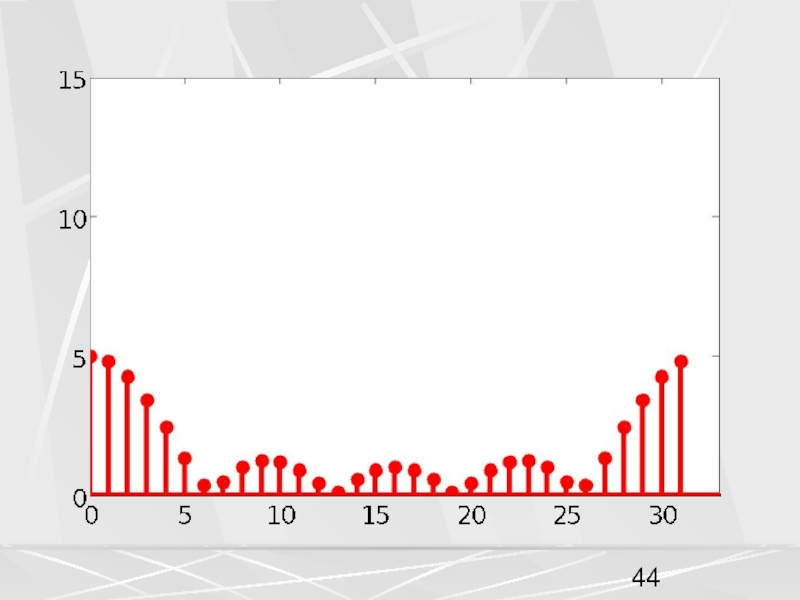
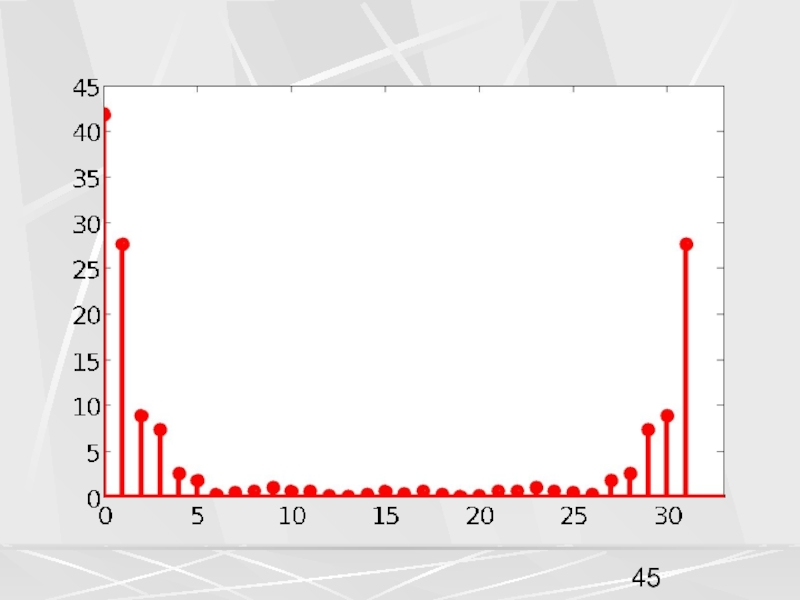
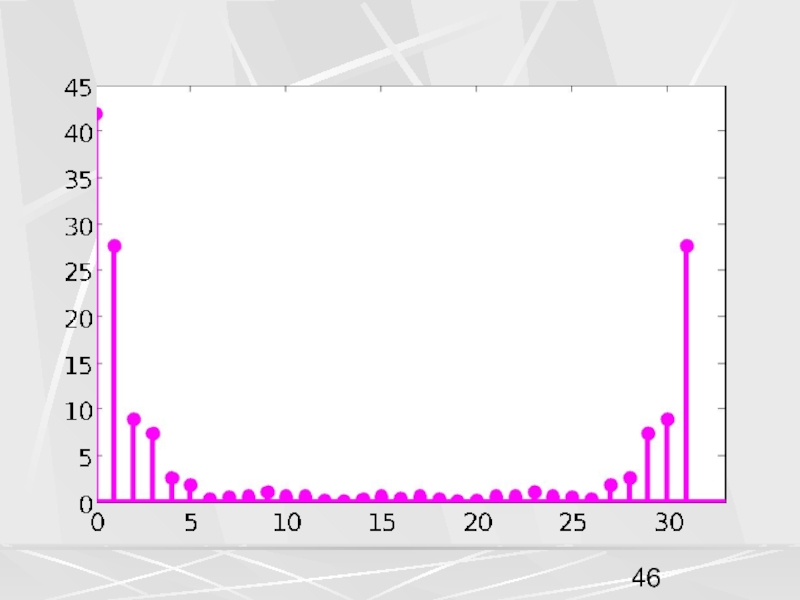
примера, рассмотрим вектор x, компоненты которого убывают по экспоненциальному закону.

(1)

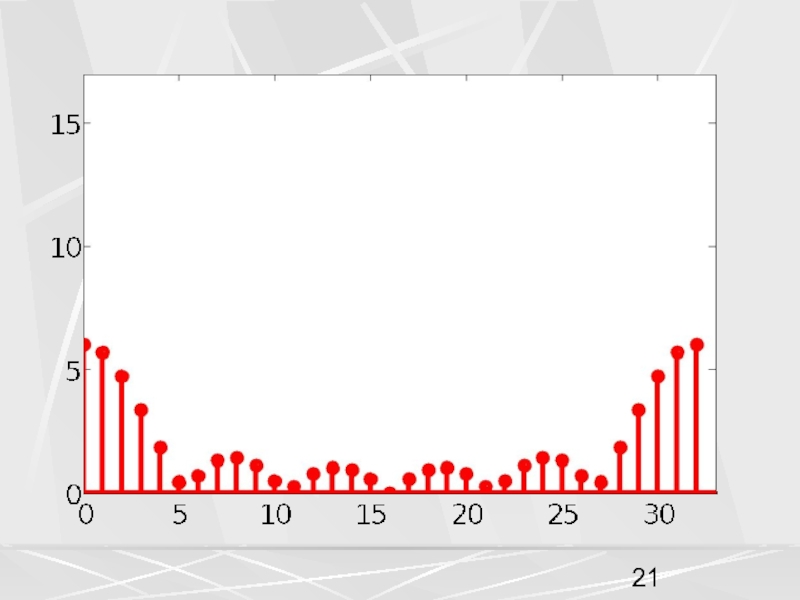
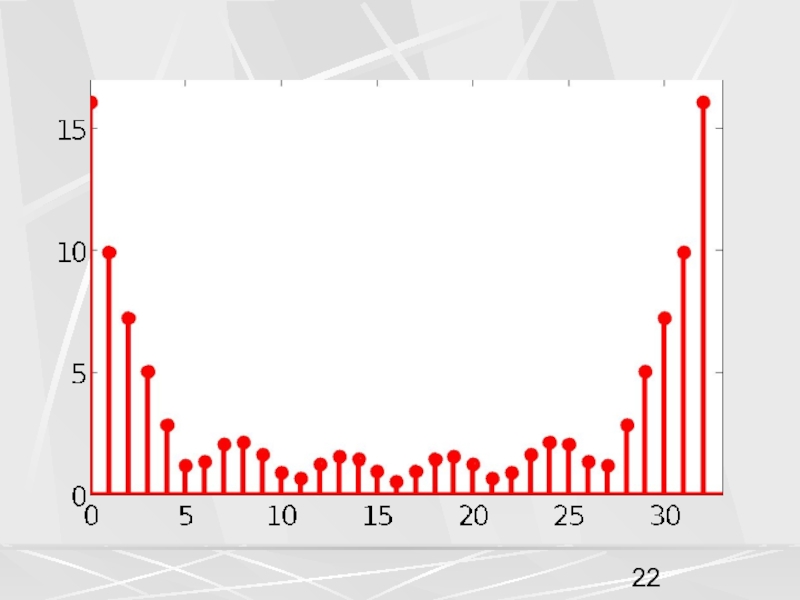
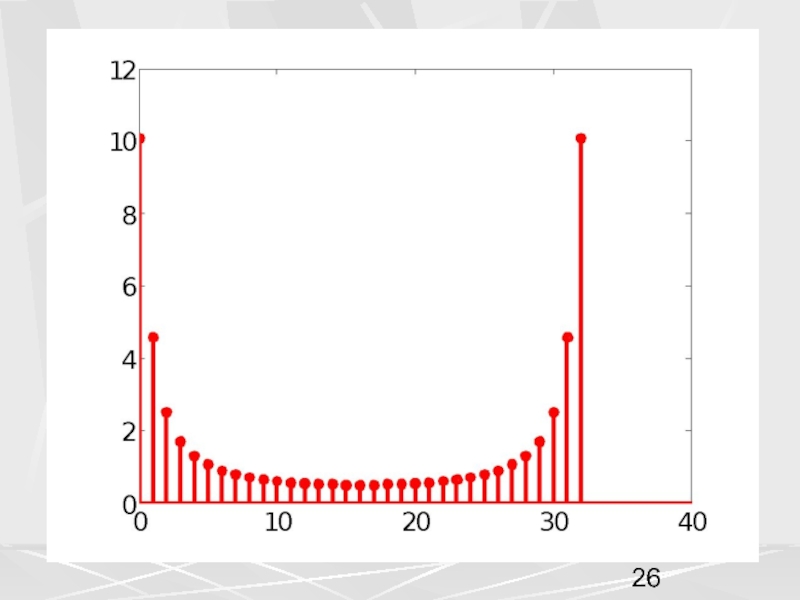
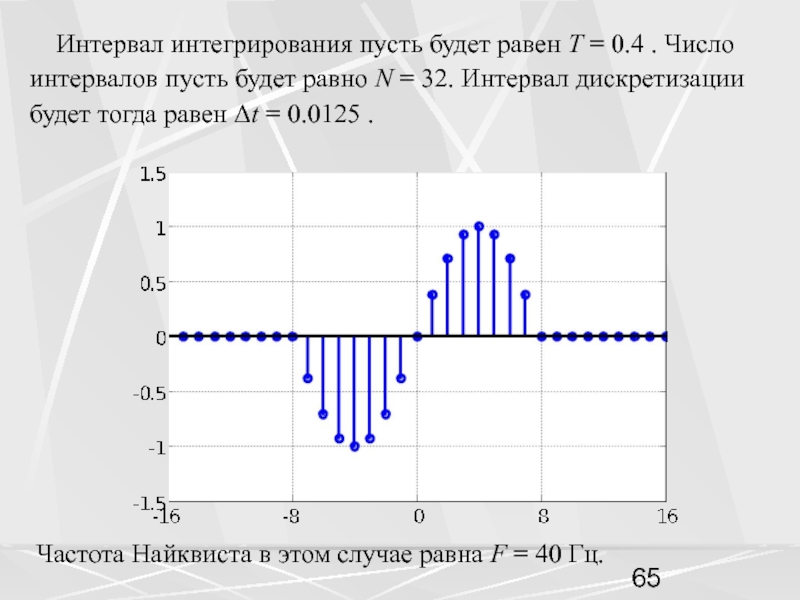
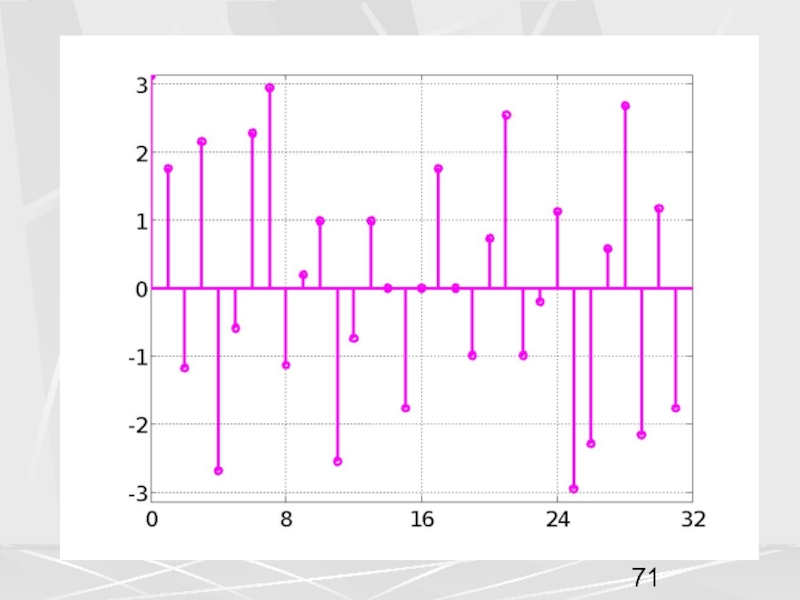
Совокупность компонент вектора, часто будем называть числовой последовательностью. Пусть период числовой последовательности равен N =32 , а коэффициент в экспоненте a = 0.1. График этой последовательности показан на рисунке. На горизонтальной оси отложены номера компонент.

что символически выражается следующим образом.

Компоненты вектора X

(2)

Эта сумма называется прямое ДПФ.

говоря, последовательностью комплексных чисел. Поэтому интересно построить графики для модуля

(3)

В формуле (3) первое соотношение является аналогом АЧХ, а второе аналогом ФЧХ. В нашем примере графики амплитуды и аргумента показаны на рисунках.

индекса k, то обнаруживаются интересные свойства ДПФ.
Во-первых, легко показать, что

(4)

На рисунке показана эта ситуация.

свойство. График АЧХ симметричен относительно 17-ого элемента. В общем случае

(5)

если N - четное число (в нашем случае это 32), если N - нечетное число, то такого элемента не существует.

Во-вторых, последовательность ДПФ является периодической последовательностью, с периодом равным числу N .

(6)

! Доказать самостоятельно свойство (6).

лекции.
1. Свойства симметрии. Если вещественный вектор x с периодом

(7)

для модуля и аргумента будет означать следующее.

(8)
Это же можно

В качестве первой последовательности возьмем последовательность, рассмотренную выше

(10)

на m позиций компонент вектора-сигнала, соответствует умножение компонент вектора-сигнала на

(11)

Следствие. Инвариантность амплитудного спектра относительно циклических сдвигов. При любом циклическом сдвиге амплитуда компонентов ДПФ не меняется.

у которой компоненты убывают по экспоненциальному закону. Возьмем период равный

Результат показан на следующих трех рисунках.

(13)

Здесь предполагается, что компоненты векторов a и b равны нулю для следующих значений индексов.

(12)

a и b одинаковые и равны N , то период

Второе, как легко показать из формул (12), (13) последняя компонента свертки всегда равна нулю.

(14)

! Доказать самостоятельно свойство (14)

и , то период

имеет ДПФ равный произведению ДПФ исходных векторов.

(28)
Важное замечание!! В

(29)

b, c строится не по периоду N , а по

(30)

Возьмем два вектора с периодом N = 16 . Пусть первый вектор имеет компоненты, убывающие по экспоненциальному закону.

(31)

Эти два вектора дополняем нулями до векторов с

имеются средства для вычисления дискретного преобразования Фурье. Преобразование ДПФ, например,

X = fft(x);

. Вызов этой функции осуществляется следующим образом.
x = ifft(X);

(33)

Отличие этих формул связано с тем, что нумерация

пор дискретное преобразование Фурье рассматривалось формально как некоторое линейное преобразование

(35)

отсчеты дискретного сигнала. Предположим, что дискретный сигнал определен конечным

Другими словами для n < 0 или для n > N – 1 можно считать . Поэтому ряд (35) заменяется конечной суммой.

(36)

с периодом 2F . На периоде [0, 2F] выберем N

(37)

В формуле (37) величина Δf называется шагом частотной дискретизации. Подставим дискретные значения частоты (37) в формулу спектра (36). В результате получим.

(38)

является ДПФ для последовательности .


(39)
Сравнивая формулы (38)

(40)

дискретного сигнала

то связь (40) можно изобразить в виде.

(41)

является по сути дела, дискретным спектром дискретного сигнала.

(44)

задача нахождения спектра сигнала решается просто. Чаще всего этого сделать

равен интегралу с конечными пределами.

(45)
Этот интеграл можно

сигнала берем в

В методе прямоугольников интеграл (45) заменяем следующей суммой

(46)

дискретного сигнала. Мы видим, что формулы очень похожи.

(48)

В формуле (47) нумерация другая.

(49)

мы рассматриваем непрерывный сигнал для положительных и отрицательных моментов времени.

Обычно нас интересует спектр, как для положительных значений частоты f > 0 ,так и для отрицательных значений частоты f < 0. Поэтому, определим дискретные значения частоты следующим образом

(50)

получаем

(51)
Рассмотрим для примера, непрерывный сигнал заданный

(52)

а длительность импульса равна соответственно a = 0.2 с. График этого сигнала

. Число интервалов пусть будет равно N = 32. Интервал дискретизации будет

Частота Найквиста в этом случае равна F = 40 Гц.

было похоже на последовательность, для которой можно найти ДПФ.

(53)
Для

(54)

с помощью ДПФ (54)

(55)
Построим график спектра (55).

дискретного спектра (51) непрерывного сигнала и ДПФ (54) осуществляется простыми

(56)

! Доказать самостоятельно первую формулу (56).

надо иметь алгоритмы быстрого вычисления дискретного преобразования Фурье. Здесь мы

Запишем ДПФ в следующем виде:

(57)

N суммы (57). Рассмотрим ДПФ размерности

(58)

Тогда ДПФ примет вид.

(59)

видеть, требуется около комплексных сложений с

Введем вектор

(60)

который является вектором четных отсчетов вектора X.

следующее соотношение

(62)

четными и нечетными членами. При этом учтем формулы (60), (61),

(63)

Две суммы в (63) обозначим следующим образом.

(64)

что первая формула (64) – это ДПФ вектора

Учитывая (64) формулу (63) можно переписать в следующем виде.

(65)

Далее можно показать, что имеют место следующие соотношения.

замену

(67)

помощи уравнений (68) мы выразили коэффициенты ДПФ размерности



(69)

Таким образом, вычисление - точечного

с использованием уравнений (68) потребует порядка

операция сведения к двум ДПФ меньшей размерности выполняется