Слайд 1Первичная обработка данных
статистического наблюдения
Слайд 2Результатом первичной группировки собранных статистических данных является построение ряда распределения,
под которым понимают группировку наблюдений за значениями одного и того
же показателя в один и тот же момент времени по разным единицам совокупности.
Ряд распределения всегда состоит из двух частей: значений вариант и соответствующих им частот (или частостей).
Вариантой называется значение, которое может принимать признак в ряду распределения, частотой – количество единиц наблюдения, обладающих значением данной варианты. Сумма частот всегда равна объему совокупности. Иногда вместо частот рассчитывают частости – это частоты, выраженные либо в долях единицы (тогда сумма всех частостей равна 1), либо в процентах к объему совокупности (сумма частостей будет равна 100 %).
Слайд 3Ряды распределения делятся на атрибутивные и вариационные в зависимости от
признака, положенного в основу построения ряда.
Если признак качественный, то ряд
распределения называется атрибутивным.
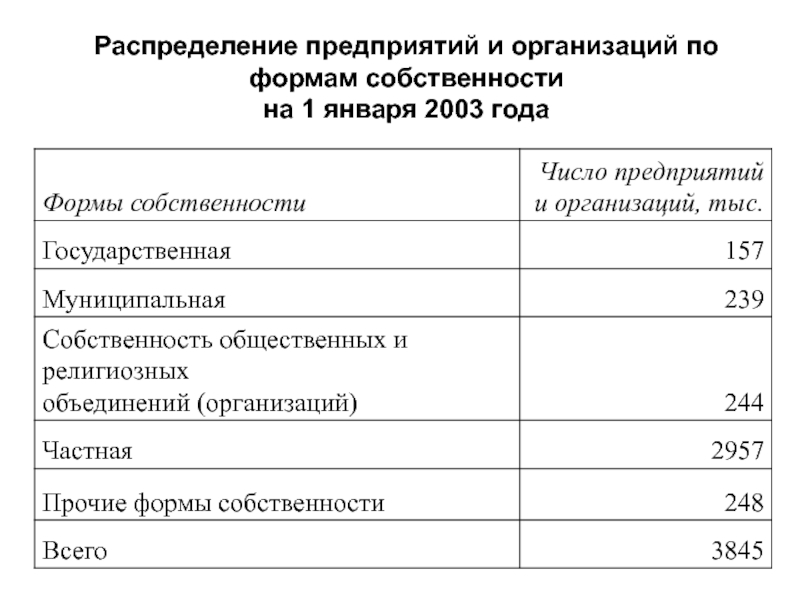
Примером атрибутивного ряда является распределение предприятий и организаций по формам собственности.
Слайд 4Распределение предприятий и организаций по формам собственности
на 1 января
2003 года
Слайд 5Если признак, по которому строится ряд распределения, количественный, то ряд
называется вариационным.
Вариационные ряды бывают дискретные и интервальные.
У дискретных
рядов значения признака выражены конкретными числами, чаще всего целыми (варианты представляют собой перечень чисел), у интервальных рядов значения показателя задаются в виде интервалов.
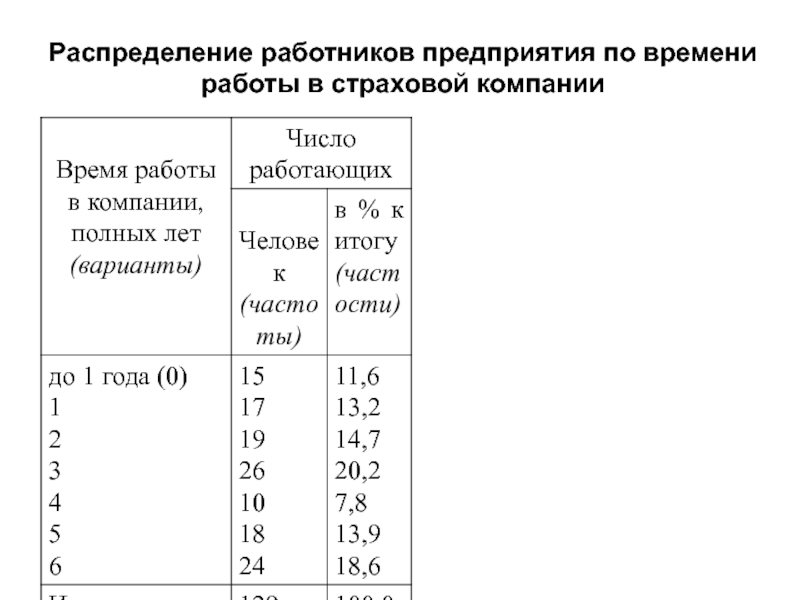
Слайд 6Распределение работников предприятия по времени
работы в страховой компании
Слайд 7
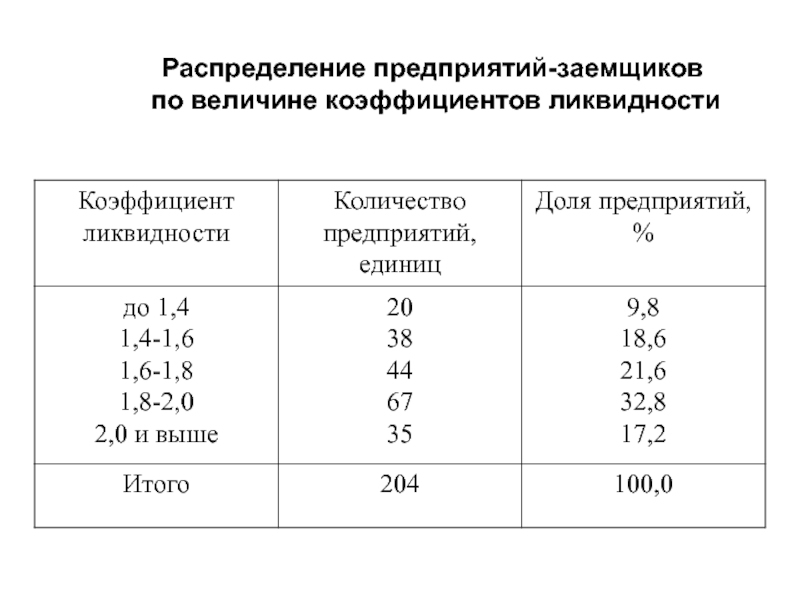
Распределение предприятий-заемщиков
по величине коэффициентов ликвидности
Слайд 8Интервалы интервального вариационного ряда имеют две границы: нижнюю и верхнюю.
Интервалы могут быть открытыми и закрытыми. У открытых нет одной
из границ.
При построении интервального ряда в зависимости от характера разброса значений признака используют как равные интервальные промежутки, так и неравные.
Слайд 9Если признак принимает ограниченное число значений, обычно не больше 10,
строят дискретные ряды распределения.
Если вариант больше, то дискретный ряд
теряет свою наглядность и уже целесообразно использовать интервальную форму вариационного ряда.
Кроме того, при непрерывной вариации признака, когда его значения в определенных пределах отличаются друг от друга на сколь угодно малую величину, также строят интервальный ряд распределения.
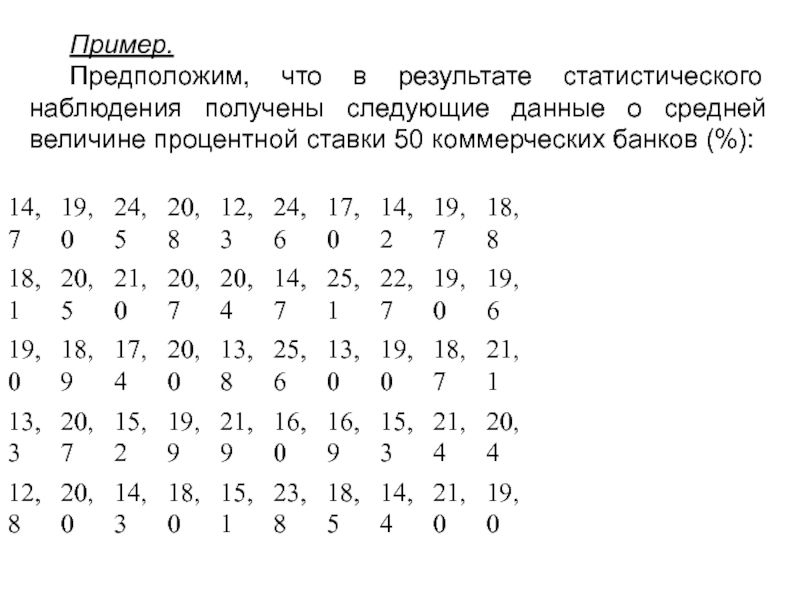
Слайд 10Пример.
Предположим, что в результате статистического наблюдения получены следующие данные о
средней величине процентной ставки 50 коммерческих банков (%):
Слайд 11Ход построения интервального ряда распределения с равными интервалами
1. Определим число
интервалов.
Число интервалов на практике часто задается самим исследователем исходя из
задач каждого конкретного наблюдения, но может вычисляться и математически, если распределение значений признака близко к нормальному закону распределения, по формуле Стерджесса:
где п – число интервалов,
N – объем совокупности (число единиц наблюдения).
Для нашего примера:
Слайд 122. Определим величину интервалов (i) по формуле:
Для нашего примера:
Интервалы
вариационного ряда наглядны, если их границы имеют «круглые» значения, поэтому
округлим величину интервала «1,9» до «2», а минимальное значение признака «12,3» до «12,0».
Слайд 133. Определим границы интервалов.
Интервалы, как правило, записывают таким образом, чтобы
верхняя граница одного интервала являлась одновременно нижней границей следующего интервала.
Для нашего примера получим:
12,0 – 14,0; 14,0 – 16,0; 16,0 – 18,0; 18,0 – 20,0; 20,0 – 22,0; 22,0 – 24,0; 24,0 – 26,0.
Подобная запись означает, что признак непрерывный.
Если же варианты признака принимают строго определенные значения, например, только целые, но их количество слишком велико для построения дискретного ряда, то можно создать интервальный ряд, где нижняя граница интервала не будет совпадать с верхней границей следующего интервала.
Кроме того, в нашем примере мы могли бы сделать первый и последний интервалы открытыми, т.е. записать: «до 14,0», «24,0 и выше».
Слайд 144. Подсчитаем частоты.
При подсчете частот, если значение признака попадает
на границу интервала, то данная единица приписывается к тому интервалу,
для которого ее значение является верхней границей, например, значение «16,0» в нашем примере будет относиться ко второму интервалу.
Слайд 15Результаты группировки:
Распределение коммерческих банков
по величине кредитной ставки