Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Изучение статистических связей между явлениями
Содержание
- 1. Изучение статистических связей между явлениями
- 2. План урокаТипы и характеристики связейВиды и формы
- 3. Типы и характеристика связейБалансовая связьКомпонентные связиФакторные связи
- 4. Типы и характеристика связейБалансовая связь показателей коммерческой
- 5. Типы и характеристика связейКомпонентные связи показателей коммерческой
- 6. Типы и характеристика связейФакторные связи в коммерческой
- 7. Виды и формы связей Существующие виды и
- 8. Виды и формы связей По направлению:Прямая -
- 9. Виды и формы связей По аналитическому выражению
- 10. Виды и формы связей По тесноте связи
- 11. Корреляционные связи и их виды Понятие теории
- 12. Корреляционные связи и их видыКорреляционно-регрессионный метод исследования
- 13. Корреляционные связи и их виды Корреляционный метод
- 14. Корреляционные связи и их виды Задачи корреляционного
- 15. Корреляционные связи и их виды Корреляционный метод
- 16. О тесноте связи свидетельствует абсолютная величина коэффициента
- 17. Корреляционные связи и их видыВ основе исчисления
- 18. УРАВНЕНИЯ РЕГРЕССИИ Регрессионный метод анализаЗависимости между признаками
- 19. Практика применения корреляционно-регрессионного метода анализаПРИМЕР:Имеются следующие данные
- 20. Практика применения корреляционно-регрессионного метода анализа1. Для подтверждения
- 21. Практика применения корреляционно-регрессионного метода анализаВывод: На основе
- 22. Практика применения корреляционно-регрессионного метода анализа2. Для определения
- 23. Практика применения корреляционно-регрессионного метода анализа
- 24. Практика применения корреляционно-регрессионного метода анализаЛинейный коэффициент корреляции
- 25. Практика применения корреляционно-регрессионного метода анализа3. В целях
- 26. Практика применения корреляционно-регрессионного метода анализаСпособом наименьших квадратов
- 27. Практика применения корреляционно-регрессионного метода анализаПодставляют значение а1
- 28. Практика применения корреляционно-регрессионного метода анализа4. Используя полученную
- 29. Практика применения корреляционно-регрессионного метода анализаТак как уравнение
- 30. Практика применения корреляционно-регрессионного метода анализаῩх=а0+ а1х1+а2х2+…+апхп, которое
- 31. Общие вопросы к изученной темеИзучение взаимосвязей
- 32. Вопросы для самопроверкиКакие виды связей показателей коммерческой
- 33. Скачать презентанцию
План урокаТипы и характеристики связейВиды и формы связиКорреляционные связи и их видыУравнения регрессииПрактика применения корреляционно-регрессионного метода анализа
Слайды и текст этой презентации
Слайд 4Типы и характеристика связей
Балансовая связь показателей коммерческой деятельности характеризует зависимость
между источниками формирования ресурсов (средств) и их использованием.
Он+П=В+Ок
Он — остаток
товаров на начало изучаемого периода;П—поступление товаров за период;
В — выбытие товаров в изучаемом периоде;
Ок — остаток товаров на конец периода.
Слайд 5Типы и характеристика связей
Компонентные связи показателей коммерческой деятельности характеризуются тем,
что изменение статистического показателя определяется изменением компонентов, входящих в этот
показатель, как множителиIqp = IP * Iq.
Iqp — индекс товарооборота в фактических ценах;
IP — индекса товарооборота в сопоставимых ценах;
Iq — индекс цен.
Слайд 6Типы и характеристика связей
Факторные связи в коммерческой деятельности характеризуются тем,
что они проявляются в согласованной вариации изучаемых показателей:
При функциональной связи
изменение результативного признака у всецело обусловлено действием факторного признака х: y=f(x).
При корреляционной связи изменение результативного признака у обусловлено влиянием факторного признака х не всецело, а лишь частично, так как возможно влияние прочих факторов Ɛ:
у = ψ (х)+ɛ
Слайд 7Виды и формы связей
Существующие виды и формы связей могут
различаться по:
существу
характеру
направлению
тесноте
аналитическому выражению.
Слайд 8Виды и формы связей
По направлению:
Прямая - это связь, при
которой с ростом значений факторного признака растут значения результативного признака.
Обратная - это связь с увеличением значений одного признака величина другого признака, от него зависящего, уменьшается.
Слайд 9Виды и формы связей
По аналитическому выражению :
Линейная - связь,
которая может быть выражена аналитическим уравнением прямой линии.
Криволинейная – связь,
которая может быть выражена уравнением какой-либо кривой линии (гиперболы, параболы, логарифмической, степенной, показательной и др.).Слайд 10Виды и формы связей
По тесноте связи между социальными или
экономическими явлениями выделяют связи слабые и сильные (тесные), которые измеряются
с помощью специальных коэффициентов. Связь двух признаков выявляет парную корреляцию, а влияние нескольких факторных признаков на результативный - выявляет многофакторную (множественную) связь.Слайд 11Корреляционные связи и их виды
Понятие теории корреляции
корреляционно-регрессионный метод исследования нацелен
на:
выявление зависимости признаков;
выбор формы связи и нахождение её аналитического выражения;
измерение
степени тесноты связи;расчет теоретических уровней;
анализ полученных результатов.
Слайд 12Корреляционные связи и их виды
Корреляционно-регрессионный метод исследования состоит из двух
этапов. К первому этапу относится корреляционный анализ, а ко второму
- регрессионный анализ.Корреляционный метод исследования:
выявляет зависимость между признаками;
устанавливает форму связи и находит ее аналитическое выражение;
измеряет степень тесноты связи.
К задачам регрессионного анализа относится:
выражение аналитической формы связи в виде построения уравнения связи (регрессии);
расчет на основе этого уравнения теоретических уровней, т.е. ожидаемые, планируемые или прогнозируемые показатели на предстоящий период.
Слайд 13Корреляционные связи и их виды
Корреляционный метод анализа
Задачи, поставленные перед корреляционным
методом исследования, разрешаются с помощью следующих методов анализа:
качественного анализа
с отбором взаимосвязанных признаков (факторов);графического метода;
метода определения тесноты связи.
Слайд 14Корреляционные связи и их виды
Задачи корреляционного анализа
Выявление зависимости между признаками
– предполагает качественный анализ в обработке первичного материала, отбор факторов,
а выявление зависимостей определяется в основном с помощью метода группировок.выбор формы связи осуществляется с помощью графического метода с последующим нанесением на этот же график результатов, полученных на основании построенной корреляционно-регрессионной модели.
Слайд 15Корреляционные связи и их виды
Корреляционный метод анализа
а) прямая линейная зависимость;
б)
обратная линейная зависимость;
в) зависимость отсутствует
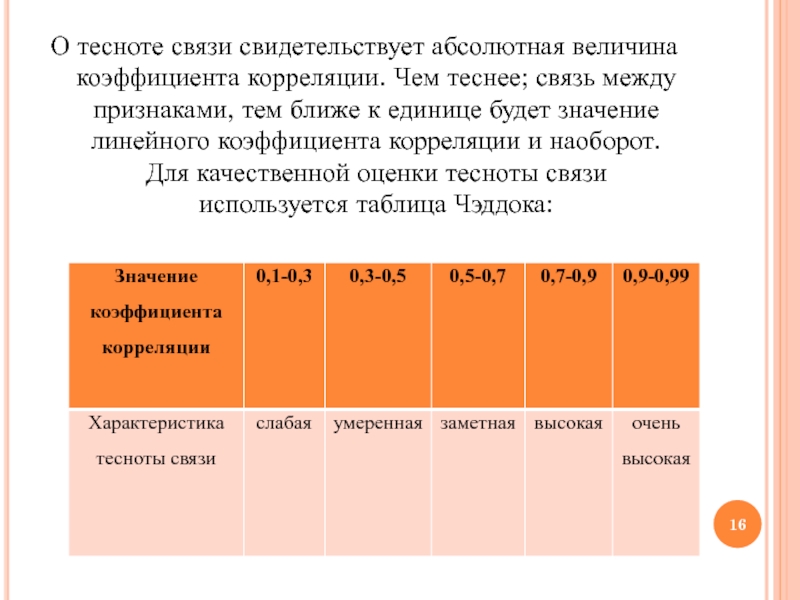
Слайд 16О тесноте связи свидетельствует абсолютная величина коэффициента корреляции. Чем теснее;
связь между признаками, тем ближе к единице будет значение линейного
коэффициента корреляции и наоборот. Для качественной оценки тесноты связи используется таблица Чэддока:Слайд 17Корреляционные связи и их виды
В основе исчисления корреляционного отношения лежит
правило сложения дисперсий
σ2y = σ2i + σ ᷈ 2y
σ2i – внутригрупповая дисперсия;
σ ᷈ 2y – межгрупповая дисперсия.
Отношение показывает, какую долю обшей дисперсии составляет дисперсия под влиянием изучаемого фактора. Извлекая квадратный корень из величины этого отношения, получаем корреляционное отношение:
Слайд 18УРАВНЕНИЯ РЕГРЕССИИ
Регрессионный метод анализа
Зависимости между признаками выражаются следующими уравнениями:
Прямой
ух = а0 + а1х;
Гиперболы
ух = а0 + а1*1/xЛогарифмической ух = а0 + а1lgx ;
Параболы 2-го порядка ух = а0 + а1х+ а2х2 и др.
Слайд 19Практика применения корреляционно-регрессионного метода анализа
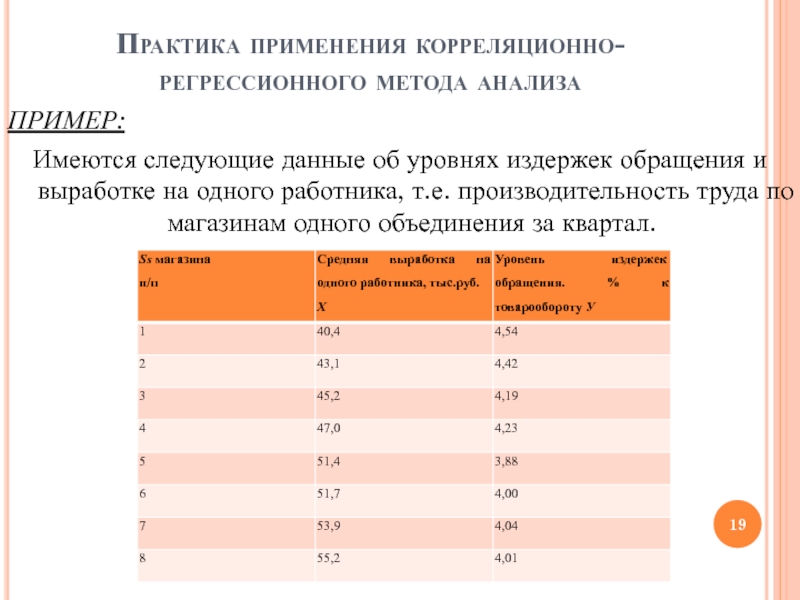
ПРИМЕР:
Имеются следующие данные об уровнях издержек
обращения и выработке на одного работника, т.е. производительность труда по
магазинам одного объединения за квартал.Слайд 20Практика применения корреляционно-регрессионного метода анализа
1. Для подтверждения положений логического (качественного)
анализа о наличии прямой зависимости между уровнем издержек обращения и
средней выработкой нанесите исходные данные на график корреляционного поля и сделайте выводы о форме связи.Решение: Для получения модели, соответствующей экономическому явлению, в расчеты необходимо брать не менее тридцати магазинов, чтобы в массе наблюдений погасить случайные явления и выявить общую закономерность.
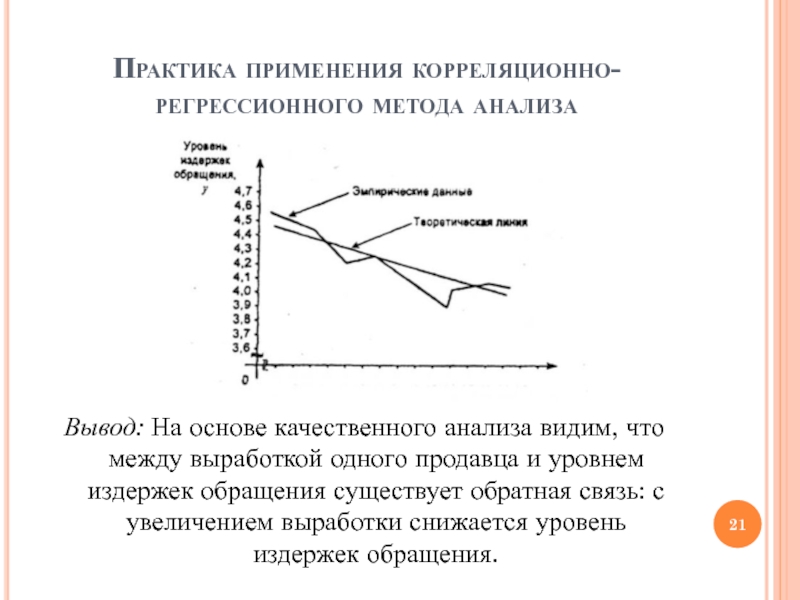
Слайд 21Практика применения корреляционно-регрессионного метода анализа
Вывод: На основе качественного анализа видим,
что между выработкой одного продавца и уровнем издержек обращения существует
обратная связь: с увеличением выработки снижается уровень издержек обращения.Слайд 22Практика применения корреляционно-регрессионного метода анализа
2. Для определения тесноты связи между
изучаемыми признаками вычислите линейный коэффициент корреляции.
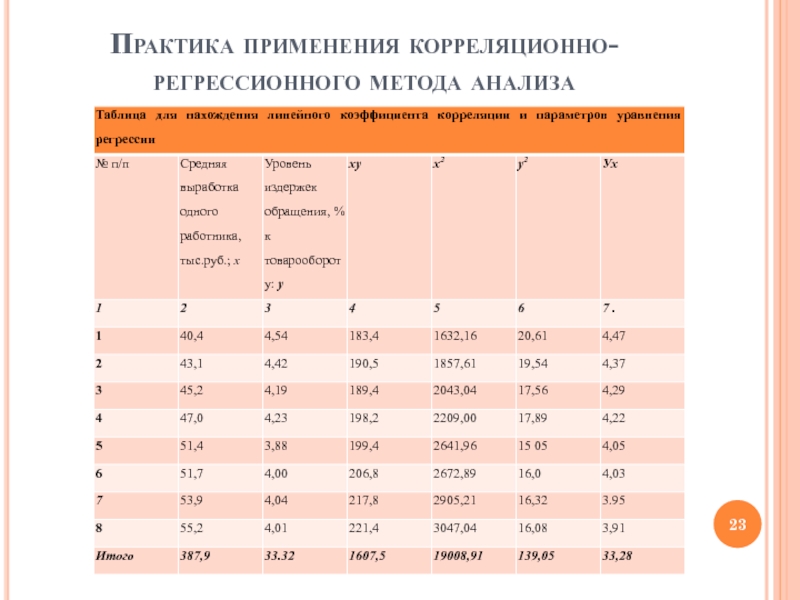
Решение: Для вычисления линейного
коэффициента корреляции произведем необходимые расчеты. Так как для расчета r и построения уравнения регрессии (связи) требуются одни и те же показатели, рассчитаем таблицу (графы 4-6).Слайд 24Практика применения корреляционно-регрессионного метода анализа
Линейный коэффициент корреляции для парной зависимости
исчисляется по следующей формуле:
Подставим значения в формулу и получим:
Вывод: Абсолютная величина линейного коэффициента коррекции свидетельствует о высокой тесноте связи между изучаемыми признаками, а знак "минус" при коэффициенте - об обратной связи.
Слайд 25Практика применения корреляционно-регрессионного метода анализа
3. В целях синтезирования модели зависимости
уровня издержек обращения от средней выработки определите уравнение прямолинейной связи
и нанесите полученную при этом теоретическую линию регрессии на график корреляционного поля.Уравнение прямой линии имеет вид:
ух = а0 + а1х;
где ух - индивидуальные значения результативного признака;
х - индивидуальные значения факторного признака;
а0 и a1 - параметры уравнения регрессии.
Слайд 26Практика применения корреляционно-регрессионного метода анализа
Способом наименьших квадратов решим систему нормальных
уравнений, находя параметры а0 и a1:
na0
+ a1Ʃx = Ʃya0Ʃx + a1Ʃx2 = Ʃxy
Подставляют значения из таблицы:
8*a0 + 387,9*a1 = 33,31
387,9*a0 + 190008,91*a1 = 1607,5
Делят каждое уравнение на коэффициенты при а0 и получают:
a0 + 48,49*a1 = 4,16
a0 + 49,0*a1 = 4,14
Вычитают из второго уравнения первое и получают:
0,51*а1 = -0,02.
Откуда а1 = -0,039
Слайд 27Практика применения корреляционно-регрессионного метода анализа
Подставляют значение а1 в первое уравнение
и получают:
а0+48,49*(-0,039)=4,16;
а0-1,89=4,16;
а0 =4,16+1,89;
а0=6,05.
Вывод: Уравнение корреляционной связи принимает вид:
ух= б,05-0,039х.Свободный член а0 характеризует уровень издержек обращения, не зависящий от выработки. Коэффициент регрессии а1 уточняет связь между у и х. Он показывает, на сколько единиц увеличивается результативный признак при измерении факторного признака на единицу в пределах установленной вариации. При увеличении выработки на 1 млн. руб. уровень издержек обращения снижается на 0,039% к обороту.
Слайд 28Практика применения корреляционно-регрессионного метода анализа
4. Используя полученную информационную модель, определите
возможное значение уровня издержек обращения для открываемого в городе нового
магазина с выработкой на одного работника 60 тыс. руб. Уровень издержек при этом составит 3,71% к товарообороту за квартал при прочих равных условиях (ух = 6,05 - 0,039 * 60 = 371).Слайд 29Практика применения корреляционно-регрессионного метода анализа
Так как уравнение регрессии составлено на
основе фактической информации по данным о восьми магазинах объединения за
квартал, то можно исчислить по нему теоретические уровни, т.е. в уравнение ух = 6,05 - 0,039 * х вместо значений х будем подставлять фактические данные о выработке каждого из восьми магазинов:№1 ух=6,05-0,039*40,4=4,47;
№2 ух=6,05-0,039*43,1=4,37
и т.д. (см. таблицу, графа 7)
Полученные значения наносим на график корреляционного поля - это будет прямая линия. Основной смысл модели - ее практическая значимость и применение в целях планирования и краткосрочного прогнозирования экономических показателей.
Слайд 30Практика применения корреляционно-регрессионного метода анализа
Ῡх=а0+ а1х1+а2х2+…+апхп, которое более полно отразит
экономический процесс и будет в полной мере являться экономико-математической моделью
при условии значимости специальных критериев.Изучение качественных показателей хозяйственно-финансовой деятельности предприятий и организаций путем моделирования экономических процессов способствует совершенствованию системы прогнозирования и планирования.
Слайд 31 Общие вопросы к изученной теме
Изучение взаимосвязей между экономическими явлениями
необходимо для планирования и прогнозирования предстоящей деятельности предприятия или отрасли.
Для
получения объективной информации выявленные связи должны иметь математическую определенность. Это осуществляется с помощью применения аппарата экономико-статистического анализа. Важнейшей особенностью экономического исследования является математическое моделирование процессов и явлений. Корреляционно-регрессионный анализ является одним методов моделирования.
Слайд 32Вопросы для самопроверки
Какие виды связей показателей коммерческой деятельности Вы можете
назвать?
Дайте понятие теории корреляции.
Какие задачи решает корреляционно-регрессионный метод исследования?
Каковы методы
анализа при корреляционном исследовании?Как графически изображаются различные виды связи показателей?
В чем смысл корреляционного анализа?
С какой целью производится регрессионный анализ?