Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Класс точности Си. Экспериментальное нормирование инструментальной погрешности
Содержание
- 1. Класс точности Си. Экспериментальное нормирование инструментальной погрешности
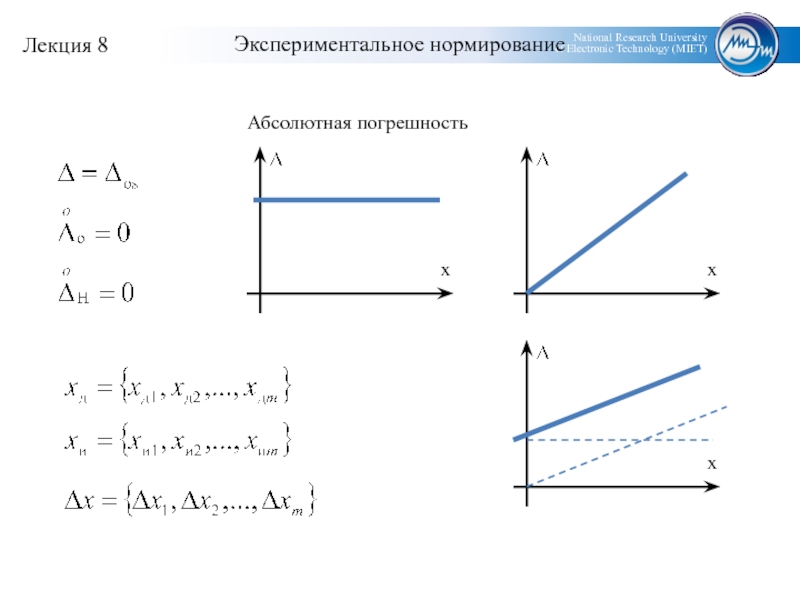
- 2. Экспериментальное нормирование
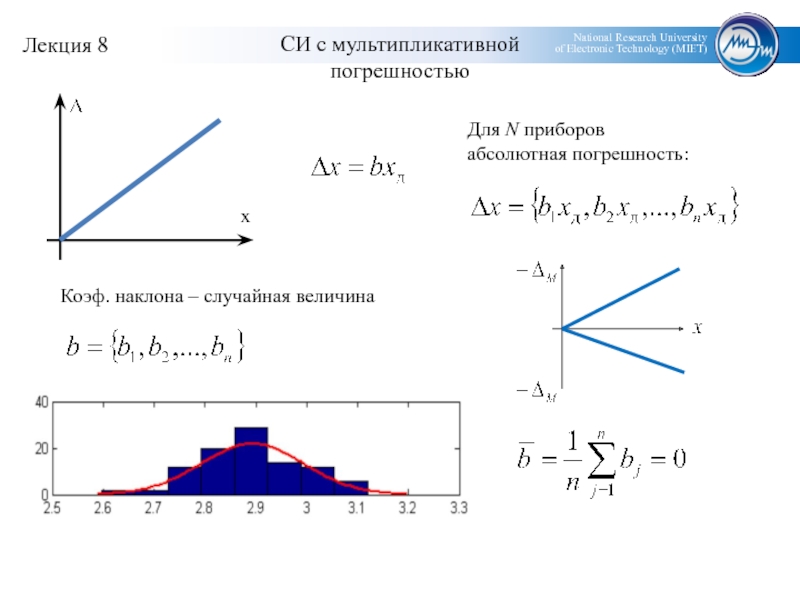
- 3. СИ с мультипликативнойпогрешностьюДля N приборов абсолютная погрешность:Коэф. наклона – случайная величина
- 4. СИ с мультипликативнойпогрешностьюНормативная документацияГраницы предельнойабсолютной погрешности:Предельное значение
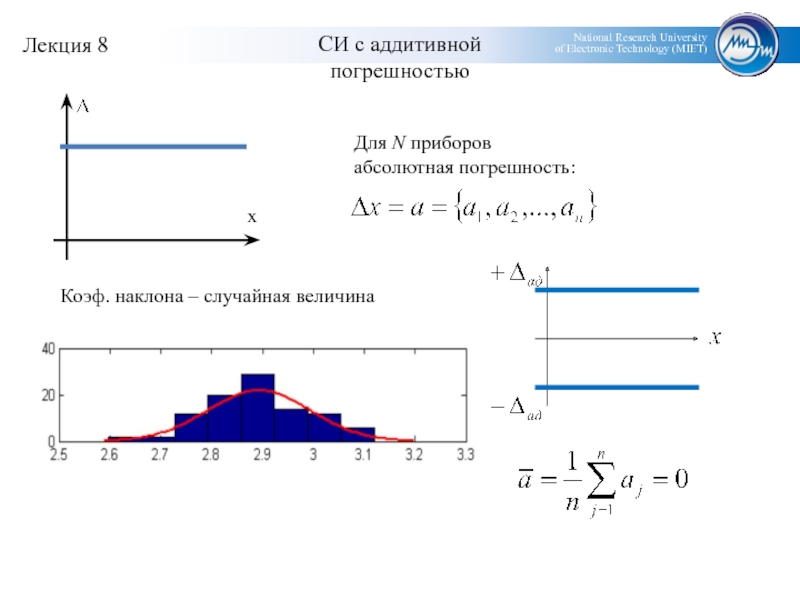
- 5. СИ с аддитивнойпогрешностьюДля N приборов абсолютная погрешность:Коэф. наклона – случайная величина
- 6. СИ с мультипликативнойпогрешностьюНормативная документацияПредельное значение Приведенной погрешности:Если
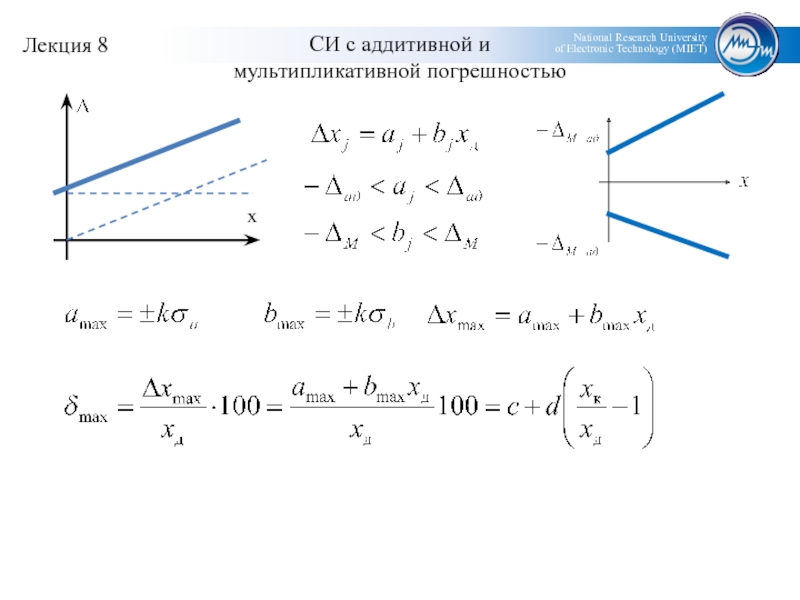
- 7. СИ с аддитивной и мультипликативной погрешностью
- 8. СИ с аддитивной и мультипликативной погрешностьюДля N приборов:
- 9. СИ с аддитивной и мультипликативной погрешностью
- 10. СИ с аддитивной и мультипликативной погрешностью
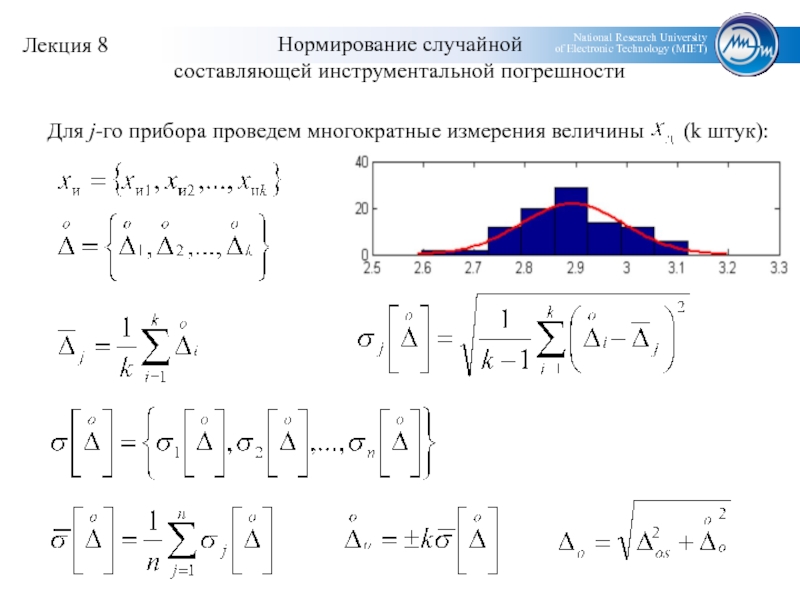
- 11. Нормирование случайной составляющей инструментальной погрешности
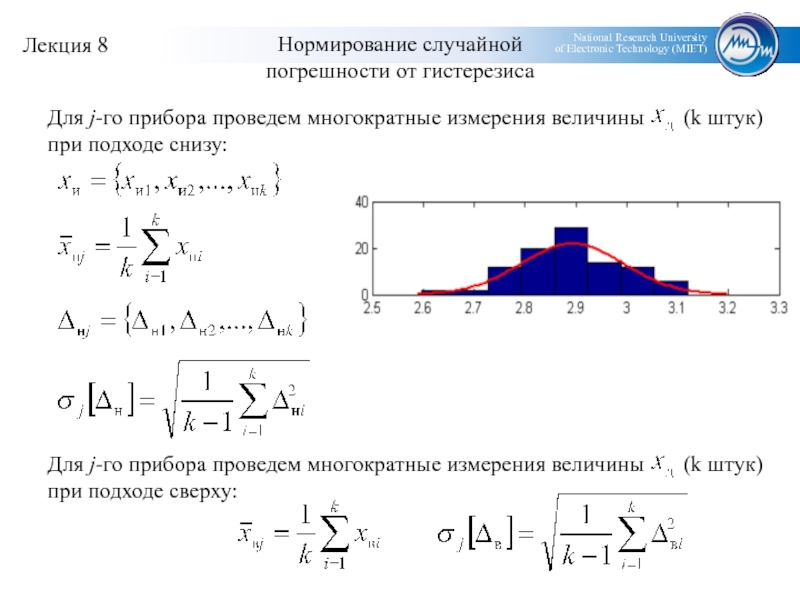
- 12. Нормирование случайной погрешности от гистерезиса
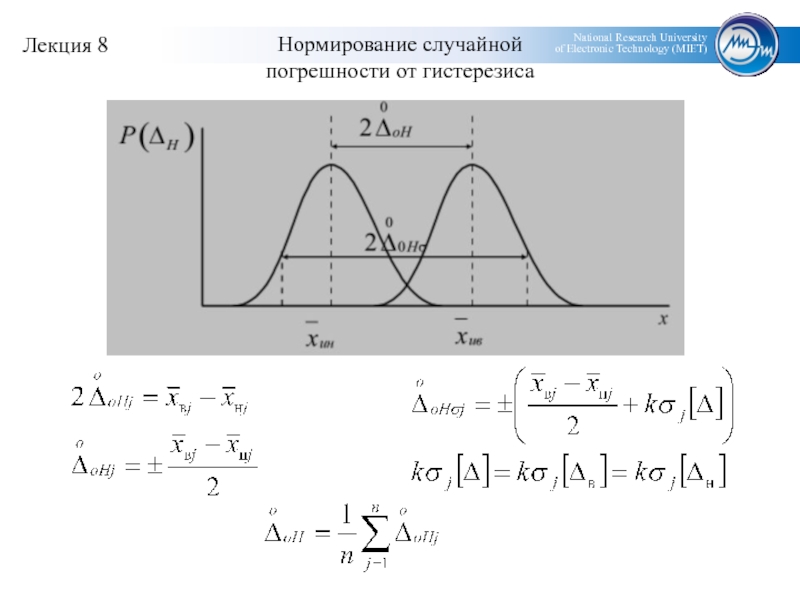
- 13. Нормирование случайной погрешности от гистерезиса
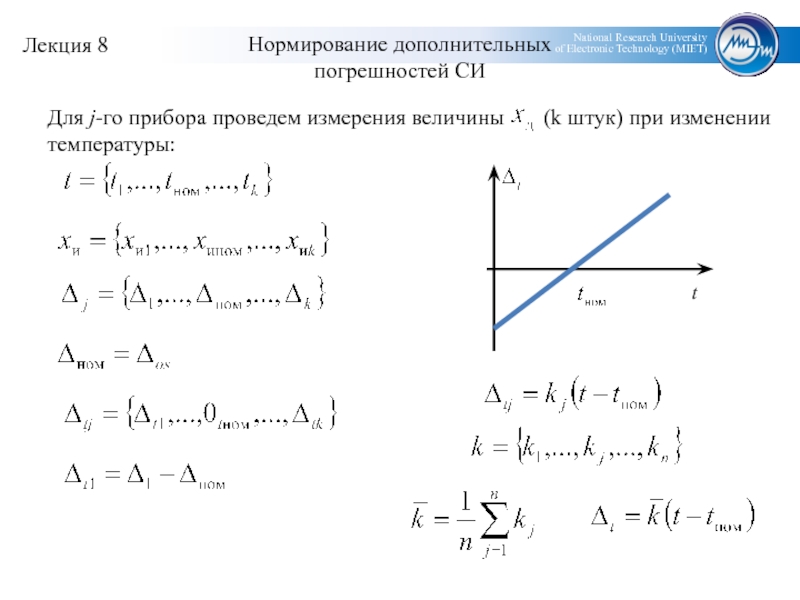
- 14. Нормирование дополнительныхпогрешностей СИ
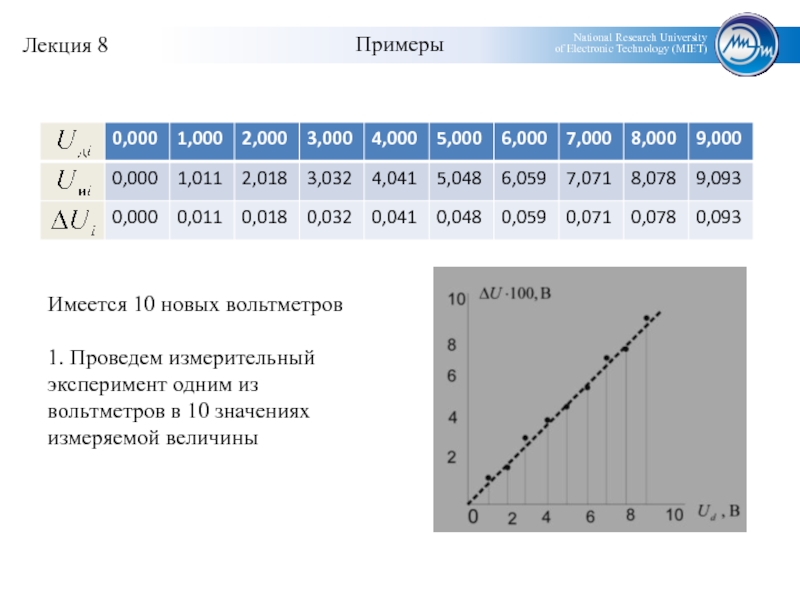
- 15. ПримерыИмеется 10 новых вольтметров1. Проведем измерительный эксперимент одним из вольтметров в 10 значениях измеряемой величины
- 16. ПримерыВторое измерение:
- 17. ПримерыПри k = 2, P = 0,9551
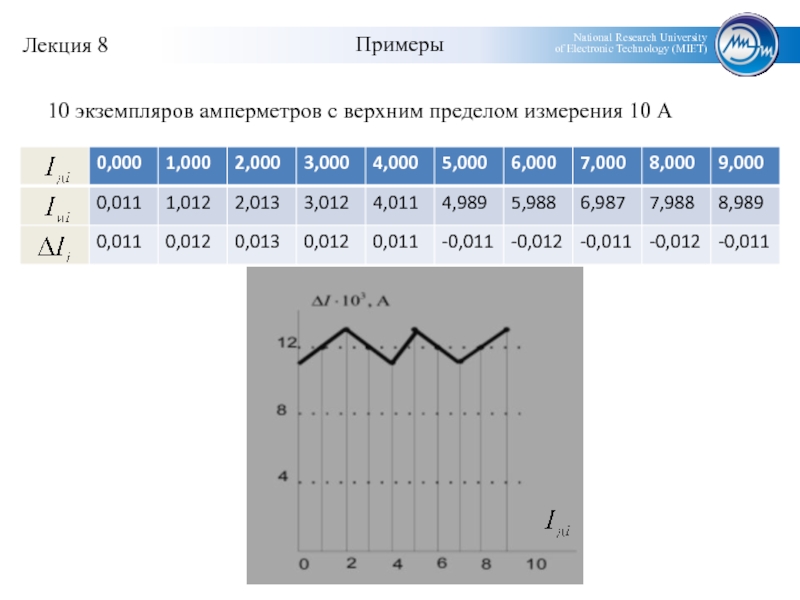
- 18. Примеры10 экземпляров амперметров с верхним пределом измерения 10 А
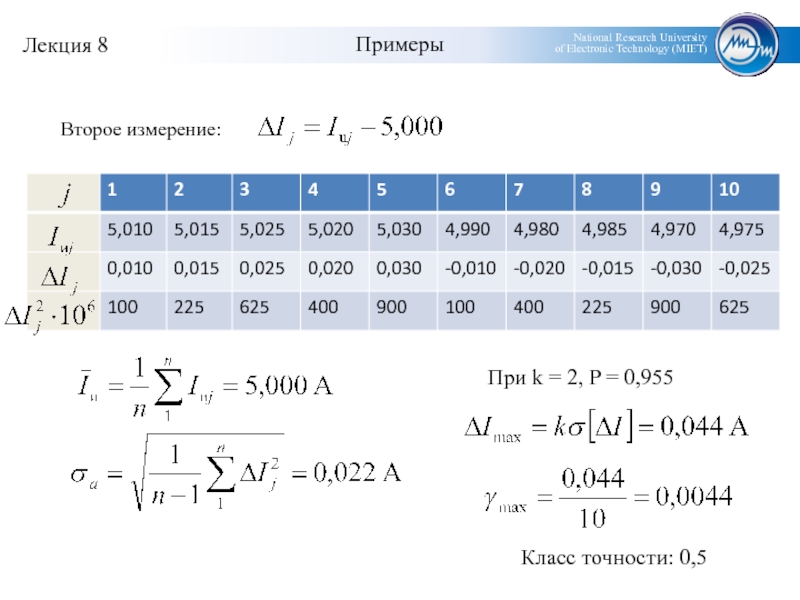
- 19. ПримерыВторое измерение:При k = 2, P = 0,955Класс точности: 0,5
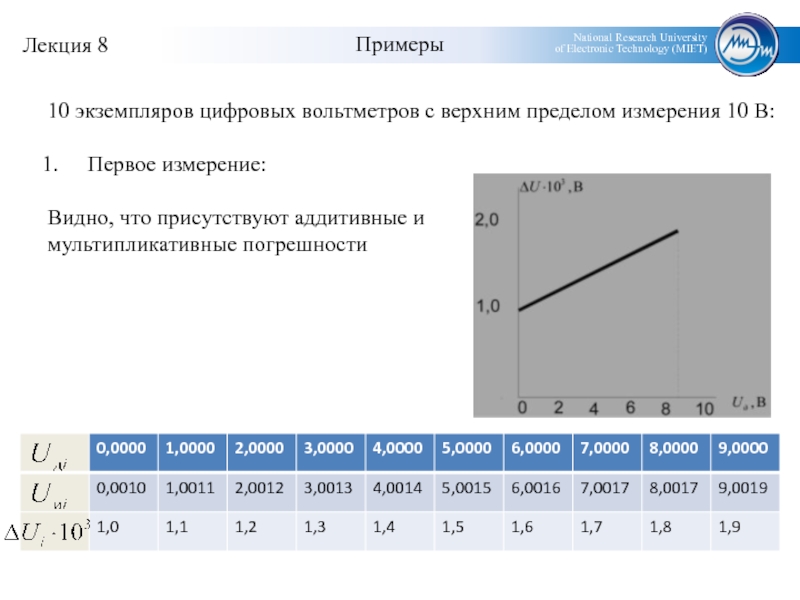
- 20. Примеры10 экземпляров цифровых вольтметров с верхним пределом измерения 10 В:Первое измерение:Видно, что присутствуют аддитивные имультипликативные погрешности
- 21. ПримерыВторое измерение – находим аддитивную составляющую
- 22. ПримерыТретье измерение:
- 23. ПримерыКласс точности: 0,6/0,025При k = 2, P = 0,955
- 24. ИсточникиОсновы метрологии. Бурдун Г.Д.ru.wikipedia.orgРМГ 29-99Основы метрологии и электрические измерения. Душин Е.М.Жуков В.К. Метрология. Теория измерений
- 25. Скачать презентанцию
Экспериментальное нормирование
Слайды и текст этой презентации
Слайд 1
Метрология,
стандартизация и сертификация
Калеев Дмитрий Вячеславович
кафедра ВТ
Лекции 8
«Класс точности СИ.
Экспериментальное нормирование инструментальной погрешности»
Слайд 3
СИ с мультипликативной
погрешностью
Для N приборов
абсолютная погрешность:
Коэф. наклона – случайная
величина
Слайд 4
СИ с мультипликативной
погрешностью
Нормативная документация
Границы предельной
абсолютной погрешности:
Предельное значение
относительной погрешности:
N
Если k
= 1, тогда P=0,683
Если k = 2, тогда P=0,955
Слайд 5
СИ с аддитивной
погрешностью
Для N приборов
абсолютная погрешность:
Коэф. наклона – случайная
величина
Слайд 6
СИ с мультипликативной
погрешностью
Нормативная документация
Предельное значение
Приведенной погрешности:
Если k = 1,
тогда P=0,683
Если k = 2, тогда P=0,955
N
Слайд 15
Примеры
Имеется 10 новых вольтметров
1. Проведем измерительный эксперимент одним из вольтметров
в 10 значениях измеряемой величины
Слайд 20
Примеры
10 экземпляров цифровых вольтметров с верхним пределом измерения 10 В:
Первое
измерение:
Видно, что присутствуют аддитивные и
мультипликативные погрешности
Слайд 24Источники
Основы метрологии. Бурдун Г.Д.
ru.wikipedia.org
РМГ 29-99
Основы метрологии и электрические измерения. Душин
Е.М.
Жуков В.К. Метрология. Теория измерений
