КРАТКАЯ ТЕОРИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ, ОСНОВНЫЕ ЭЛЕМЕНТЫ АЛГЕБРЫ

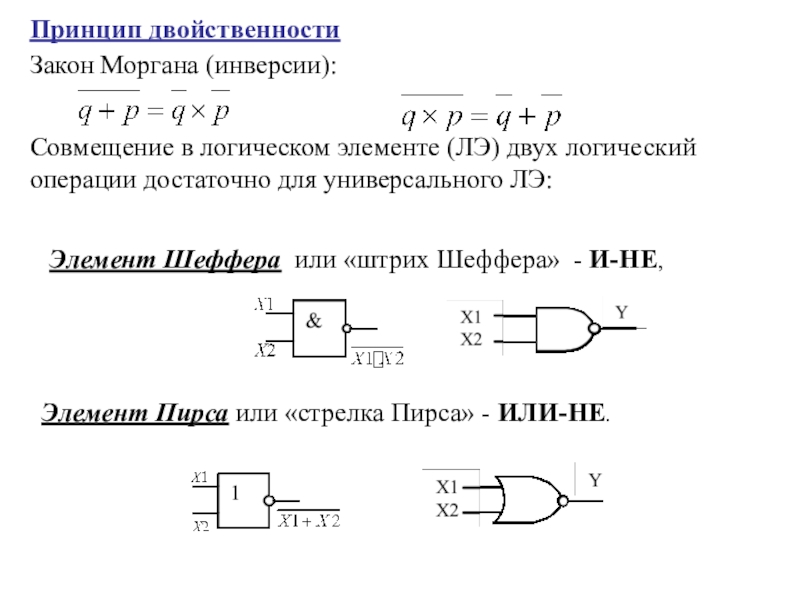
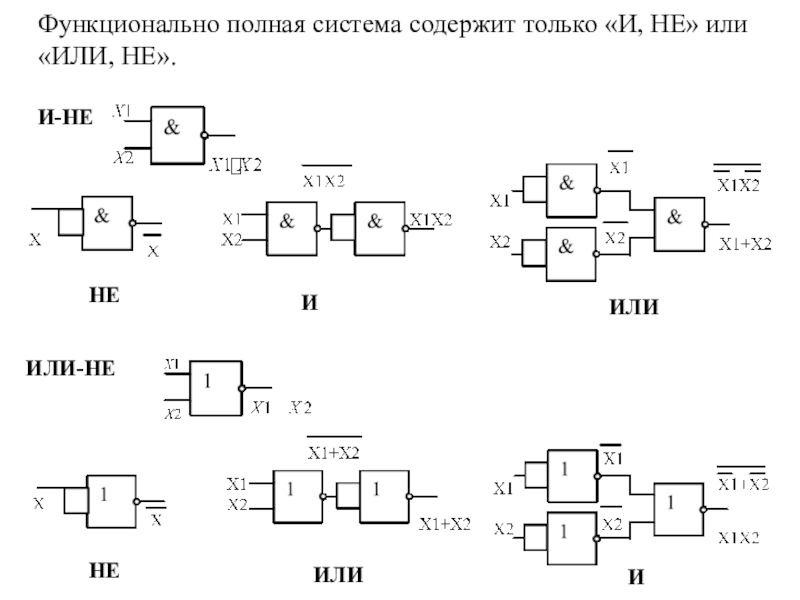
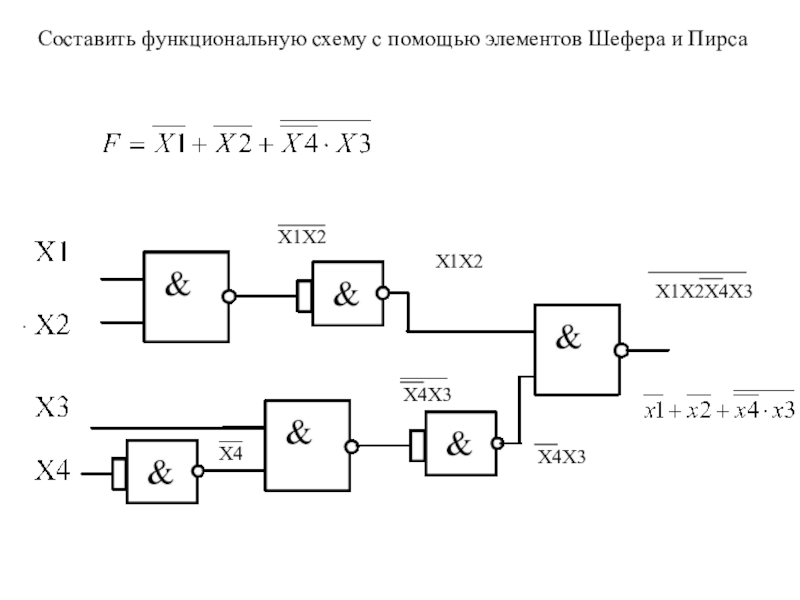
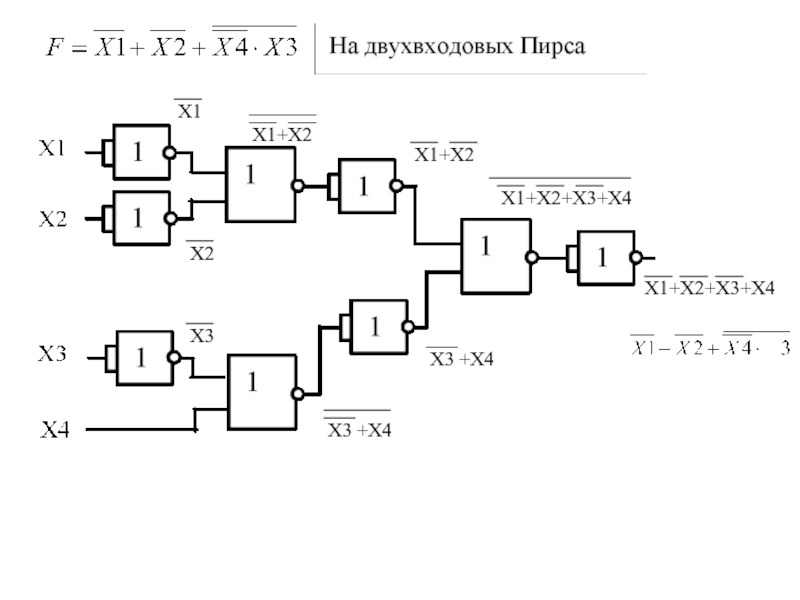
алгебры логики
Джорж Буль, 19 век, «Алгебра логики»

В устройствах ЛОC сигналы

принимают два состояния: логического «0» и логической «1» при этом
если Х=1, то Х 0 и наоборот, если Х=0, то Х1.

Высказывание - всякое утверждение относительно, которого можно сказать, оно является «истинным» или «ложным» и имеет значение истинности, равное соответственно либо «1» либо «0».
Простое высказывание или логическая переменная не зависит от истинности других высказываний.
Сложное высказывание или логическая функция - зависит от истинности составляющих его простых высказываний

высказываний (переменных).

Y=1 (истинно), если хотя бы одна из n переменных

Х =1 (если одна истинна).
Y=0 (ложно), если все из n переменных Х =0 (если все ложны)
Y=X1 или Х2 или Х3 или…или Хn
Y = Х1  Х2…  Хn Y =Х1+Х2+…+Хn.

Основные простые функции (элементы) алгебры логики.

нескольких высказываний.
Y = 1 (истинно), если все n переменные Х

= 1 ( все истинны).
Y = 0 (ложно), если хотя бы одна n переменная Х = 0 (одна ложна)

Y = Х1 и Х2 и … и Хn
Y = Х1  Х2  …  Хn или Y =Х1 ∙ Х2 ∙ … ∙ Хn.

Y =
Логическую функцию можно представить таблицей истинности

ПФ.

ПФ могут быть представлена: аналитически (формулой), таблицей истинности, принципиальной

логической схемой.

Дополнение.

Если q переменная, то ее дополнением будет переменная

Если Y= (q+p+R ) функция, то ее дополнением будет функция

которые устанавливают эквивалентность логических функций и образованных логических связей с

помощью простых логических функций И, ИЛИ НЕ.

p + q = q + p

(p+q)+R = p+(q+R)

p×q = q×p

(p×q) ×R = p× (q× R)

q×p+R = (p+R) ×(q+R)

(p+q)×R= p×R+q×R

умножения
p

+ 1 = 1 p × 0 = 0;
p + = 1 p × = 0
p= p + 0; p = p × 1
p= p + p + p… p= p × p × p…

p =

Теоремы склеивания для 2-х переменных:

p × q + × q=q;

(p + q) × ( + q)=q;

Доказательство для первой и второй теоремы:
если р=1, то результат зависит от q,
если р=0, то результат зависит от q

p(р +q) = p;

p + q = p

+ q;

Для трех и более переменных всегда справедливы высказывания:

(p + q) (p +r ) (q +r) = pq + pr + qr ;

Доказательство для первой и второй теоремы:
если , p=1 то результат не зависит от q,
если р=0, то результат не зависит от q

=1

=1

задается в виде таблиц истинности

произведений переменных,
произведения сумм переменных.
Конъюнктивная нормальная форма (КНФ).
Дизъюнктивная

нормальная форма (ДНФ) Y=f (x1,x2,x3).

Для каждой ЛФ может существовать несколько ДНФ и КНФ
Существует только один вид ДНФ и КНФ, в котором функция может быть записана единственным образом - совершенные нормальные формы СДНФ и СКНФ.
СНФ содержит все переменные (с инверсиями и без них) и нет одинаковых слагаемых для СНДФ и одинаковых произведений для СНКФ

Сумма минтерм и определяет ее СНДФ:
СНДФ и СНКФ записи ЛФ

формируются из таблиц истинности.

СНДФ

определяет СНКФ.

+ q) (p +r ) (q +r) = pq +

pr + qr

и аксиомы АЛ.
Теорема поглощения
Закон Моргана
Закон Моргана

таким методам относятся карты Карно.
КК для 2-х переменных
0
0
Карту Карно

заполняют минтермами

на один элемент, который является его дополнением.

расположены в соседних клетках, то говорят, что они «склеиваются».
Правила

группирования:

Карта Карно не имеет границ. Крайние верхние и нижние, правые и левые - соседние.
Группирование (объединение) производят по 2, 4, 8 и более соседних клеток.
Сколько объединений (групп) столько и слагаемых будет в упрощенной форме функции.
Одна клетка может входить в несколько групп.
Каждое слагаемое упрощенной функции включает только произведения переменных, которые входят во все клетки объединения.

y2

y3 y4 y5

аксиом и законов АЛ.
=1
=1
=1

y3

y4 y5

неравнозначность).
ЛФ (переключательную) можно составить из И, ИЛИ, НЕ
Функциональные логические

схемы

или «стрелка Пирса» - ИЛИ-НЕ.
Совмещение в логическом элементе (ЛЭ) двух

логический операции достаточно для универсального ЛЭ:

Закон Моргана (инверсии):

X1X2