Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 1. Векторы, линейные операции над векторами, скалярное, векторное,
Содержание
- 1. Лекция 1. Векторы, линейные операции над векторами, скалярное, векторное,
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Векторное произведение. Определение. Свойства.Определение. Упорядоченная тройка некомпланарных
- 7. Определение 1. Векторным произведением
- 8. Направление вектора с можно определить по правилу
- 9. Замечание: Определение 1 однозначно определяет вектор
- 10. ДоказательствоНеобходимость. Пусть
- 11. Теорема 2. Модуль векторного произведения равняется площади
- 12. Алгебраические свойства векторного произведения1) Антипереместительное 2) Сочетательное
- 13. § 2. Векторное произведение в координатной форме
- 14. Итак Пусть в прямоугольной декартовой системе координат
- 15. По распределительному свойству и
- 16. Раскрывая символический определитель третьего порядка по элементам
- 17. § 3. Условие колинеарности двух векторов в
- 18. § 4. Смешанное произведение трёх векторов Определение.
- 19. Доказательствоправая тройка
- 20. То есть в смешанном произведении безразлично какие
- 21. По определению 1:
- 22. § 6. Смешанное произведение в координатной формеТеорема.
- 23. Доказательство.Известно:Ч.т.д.
- 24. Скачать презентанцию
Векторное произведение. Определение. Свойства.Определение. Упорядоченная тройка некомпланарных векторов называется правой, если из конца вектора кратчайший поворот от к кажется происходящим против часовой стрелки.
Слайды и текст этой презентации
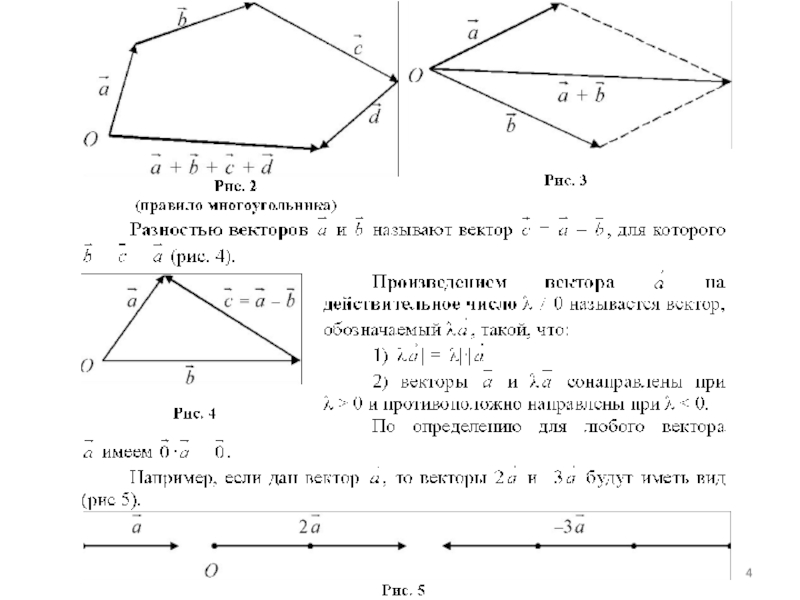
Слайд 1Лекция 1. Векторы, линейные операции над векторами, скалярное, векторное, смешанное
произведения векторов, условие компланарности векторов.
Слайд 6Векторное произведение.
Определение.
Свойства.
Определение. Упорядоченная тройка некомпланарных векторов называется правой, если из
конца вектора кратчайший поворот от
к кажется происходящим против часовой стрелки. В противном случае тройка левая.; ; ; ; ; .
Если есть две тройки либо обе правые, либо обе левые, то они называются одной ориентации.
Слайд 7Определение 1. Векторным произведением
называется третий вектор , который удовлетворяет трем условиям:
1.
2.
3.
Векторы образуют правую тройку.Обозначают: : или: [ ] ,
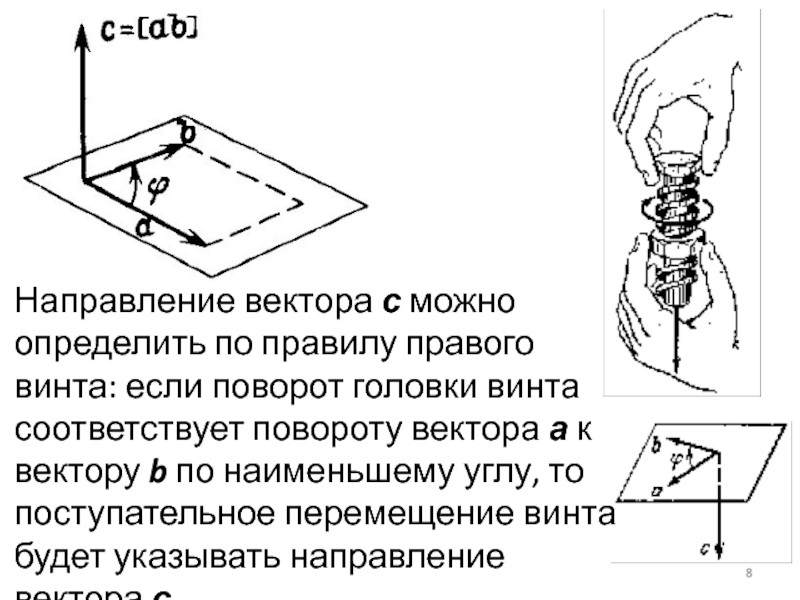
Слайд 8Направление вектора с можно определить по правилу правого винта: если
поворот головки винта соответствует повороту вектора а к вектору b
по наименьшему углу, то поступательное перемещение винта будет указывать направление вектора с.Слайд 9Замечание: Определение 1 однозначно определяет вектор в том случае,
если не один из множителей не равен 0. В случае,
если хоть один множитель = 0 , то - коллинеарны и [ ] - равно нулевому вектору.Теорема 1. Для того чтоб и были коллинеарны необходимо чтоб их векторное произведение равнялось нулевому вектору .
Геометрические свойства векторного произведения
Слайд 10Доказательство
Необходимость. Пусть
(по определению
1).Достаточность . Пусть .
Из определения 1 , либо ,
либо .
а) ,
б) пусть хотя бы один из и нуль тогда
указанный вектор нулевой, он не имеет определенного направления, следовательно, его можно считать коллинеарным любому вектору.
Слайд 11Теорема 2. Модуль векторного произведения равняется площади параллелограмма, построенного на
и , как на сторонах.
Действительно, из
определения 1 следует:Следствие:
Слайд 12Алгебраические свойства векторного произведения
1) Антипереместительное
2) Сочетательное свойства относительно скаляра
(ассоциативность)
3) Распределительное свойство относительно суммы (дистрибутивность)
Д/З: доказать одно из свойств!
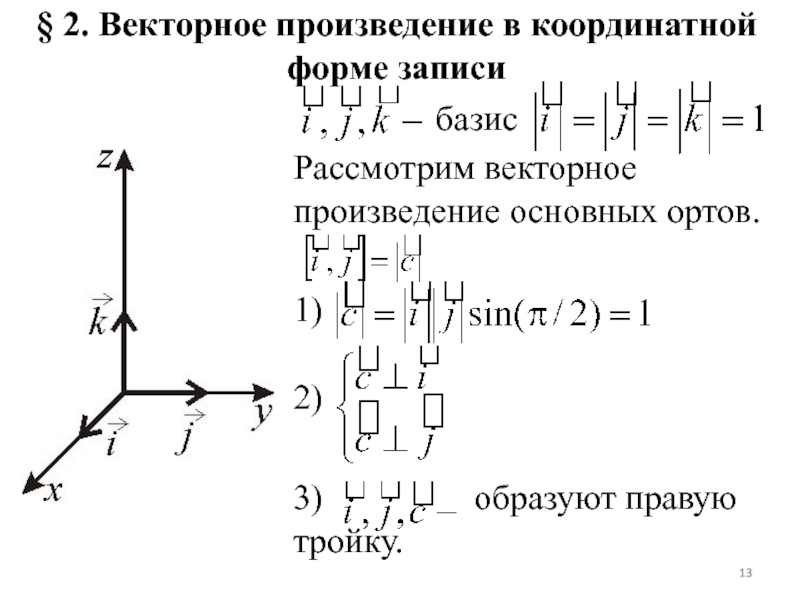
Слайд 13§ 2. Векторное произведение в координатной форме записи
базис
Рассмотрим векторное произведение основных ортов.
1)
2)
3) образуют правую тройку.
Слайд 15По распределительному свойству и можно перемножать по
правилу многочленов. По сочетательному свойству (2) можно выносить постоянный множитель за
знак векторного произведения. По антипереместительному свойству при перестановке сомножителей следует изменять знакСлайд 16Раскрывая символический определитель третьего порядка по элементам 1-ой строки мы
получим координаты в форме (**)
Слайд 17§ 3. Условие колинеарности двух векторов в координатной форме
Пусть
Значит все
три координаты этого вектора в соотношении (**) - нули. То
естьто есть если коллинеарен , то их одноимённые координаты пропорциональны.
Слайд 18§ 4. Смешанное произведение трёх векторов
Определение. Смешанным или векторно-скалярным
произведением трёх векторов , , называют число,
равное скалярному произведению на и обозначаетсяГеометрический смысл смешанного произведения
Теорема. Смешанное произведение трёх некомпланарных векторов , , равно объему параллепипеда , построенного на этих векторах как на ребрах, взятому со знаком «+» , если - правая и со знаком «-» если - левая тройка
Слайд 20То есть в смешанном произведении безразлично какие из векторов перемножаются
векторно, лишь бы не нарушить порядок сомножителей
§ 5. Условие компланарности
трёх векторов Для того чтобы были компланарными, необходимо и достаточно:
Доказательство
Достаточность. Пусть - компланарны.
Слайд 21По определению 1:
ч.т.д.
Необходимость. Пусть
По опреде-
лению 1:
Ч.т.д.
Так как их
скалярное произведение = 0
Слайд 22§ 6. Смешанное произведение в координатной форме
Теорема. Если
заданы в прямоугольной декартовой системе координат своими
координатамито их смешанное произведение
равняется определителю 3-го порядка, строками которого являются координатные строки данных векторов.