Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 15. Явления переноса в газах
Содержание
- 1. Лекция 15. Явления переноса в газах
- 2. 1. Термодинамические потоки Термодинамические потоки, связанные с
- 3. Теплопроводность - это явление, приводящее к выравниванию
- 4. На рисунке схематически изображен процесс переноса некоторой
- 5. Тогда плотность потока величины Ω можно вычислить
- 6. Диффузия Проведем описание диффузии примеси одного газа
- 7. Соответственно выражение для потока частиц Jn1 принимает
- 8. 3. Теплопроводность При описании теплопроводности в качестве
- 9. Из этой формулы следует, что с повышением
- 10. 4. Вязкость Явление вязкости газа может быть
- 11. Величина Jp имеет смысл силы, с которой
- 12. Слайд 12
- 13. Сравнивая выражения для коэффициентов переноса, получим следующие
- 14. 5. Эффузия в разреженном газе Состояние газа,
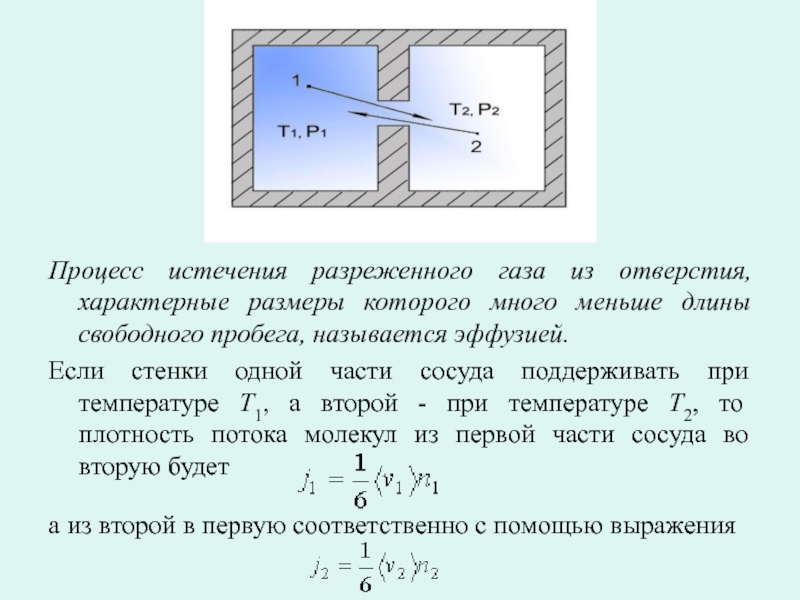
- 15. Процесс истечения разреженного газа из отверстия, характерные
- 16. где: ‹v1› и ‹v2› - средние скорости
- 17. Если температуры стенок в двух частях рассматриваемого
- 18. Скачать презентанцию
1. Термодинамические потоки Термодинамические потоки, связанные с переносом вещества, энергии или импульса из одной части среды в другую, возникают в случае, если значения тех или иных физических параметров различны в различных
Слайды и текст этой презентации
Слайд 1Лекция 15.
Явления переноса в газах.
1. Термодинамические потоки
2. Диффузия.
3. Теплопроводность.
4.Вязкость.
5. Эффузия
в разреженном газе
Слайд 21. Термодинамические потоки
Термодинамические потоки, связанные с переносом вещества, энергии
или импульса из одной части среды в другую, возникают в
случае, если значения тех или иных физических параметров различны в различных точках среды. При наличии в среде различной концентрации какой-либо примеси возникают диффузионные потоки, в случае разной температуры - тепловые потоки, при различной скорости течения - потоки импульса, или количества движения. В первом случае говорят о явлении диффузии, во втором - о явлении теплопроводности, в третьем - о явлении вязкости.Диффузией называется процесс самопроизвольного выравнивания концентраций веществ в смесях. Она наблюдается в различных средах, но её скорость сильно зависит от агрегатного состояния вещества. В газах это явление происходит достаточно быстро, что мы можем, в частности, наблюдать по тому, как происходит распространение запахов в воздухе. В жидкостях явление диффузии происходит значительно медленнее и проявляется, например, при растворении в них твердых тел или при взаимном смешивании различных жидкостей. Для наблюдения диффузии в твердых телах обычно требуется очень большое время.
Слайд 3Теплопроводность - это явление, приводящее к выравниванию температуры в различных
точках среды. Интенсивность тепловых потоков при теплопроводности в твердых телах
сильно зависит от свойств тела. Наибольшую теплопроводность имеют металлы, а наименьшую - различные теплоизоляционные материалы, такие как асбест, пенопласт и т.д. Достаточно большая теплопроводность металлов связана с тем, что в них перенос теплоты осуществляется не вследствие хаотического движения атомов и молекул, как, например, в газах или жидкостях, а свободными электронами, имеющими гораздо большие скорости теплового движения.Явление вязкости или внутреннего трения наблюдается как в газах и жидкостях, так и в твердых телах. Оно приводит к возникновению силы сопротивления при движении тела в жидкости или газе, и к затуханию звуковых волн при прохождении их через различные среды. В частности, с явлением вязкого трения связан процесс затухания колебаний в механических осцилляторах.
Для количественного описания термодинамического потока вводят величину J, численно равную количеству физической величины, переносимой за одну секунду через выбранную поверхность.
Процессы переноса в газах могут быть описаны с использованием молекулярно-кинетической теории. Такое описание дает правильные выражения для уравнений переноса и приближенные формулы для расчета коэффициентов переноса.
Слайд 4На рисунке схематически изображен процесс переноса некоторой физической величины Ω
через площадку S. Будем считать, что величина Ω изменяется в
зависимости от координаты x. В качестве переносимой величи ны может выступать масса, энергия, импульс и т.д. При этом считаем, что переносимую величину можно отнести к одной молекуле.Через площадку S в направлении оси OX будет проходить поток молекул J' = j'S, а в противоположном направлении соответственно поток J'' = j''S. Переносимый в направлении оси OX поток величины Ω отличается от потока этой величины, переносимого в обратном направлении. Это связано с тем, что в рассматриваемом газе через площадку S в направлении оси OX будут проходить молекулы, характеризуемые величиной Ω(x–λ), а в противоположном - соответственно величиной Ω(x+λ), где λ – длина свободного пробега молекул газа, численно равная перемещению, которое молекула газа проходит без соударения с другими молекулами.
Слайд 5Тогда плотность потока величины Ω можно вычислить по формуле:
Считая длину
свободного пробега λ малой величиной, функцию Ω можно представит так:
Окончательно
получаем уравнение переноса для плотности потока физической величины Ω:а соответственно для потока JΩ имеем:
Стоящие в полученных выражениях величины средней скорости
Полученное уравнение переноса применимо для описания явлений диффузии, теплопроводности и вязкости в газах при отсутствии в них макроскопического перемешивания.
Слайд 6Диффузия
Проведем описание диффузии примеси одного газа в другом. Для
простоты будем считать, что оба газа имеют практически одинаковые молекулы
и их суммарная концентрация постоянна и равна величине n: n1 + n2 = n, где n1 и n2 - концентрации газов. Введение последнего условия необходимо для того, чтобы в системе не возникало макроскопическое перемешивание газов, а их взаимное проникновение происходило только за счет диффузии.Пусть концентрация диффундирующего газа n1 зависит только от одной координаты x: n1 = n1(x). Тогда физической величиной, перенос которой в данном случае осуществляется вследствие диффузии, является относительная концентрация газа, которая также зависит только от переменной x:
Подстановка этого выражения в формулу
дает уравнение диффузии в виде:
Слайд 7Соответственно выражение для потока частиц Jn1 принимает форму:
,
где введенный коэффициент D называется коэффициентом диффузии:
.
Аналогичные выражения могут быть записаны и для второго газа, имеющего концентрацию n2.
Учтя, что Jρ1 = mJn1 имеем:
,
где: ρ1 = mn1 - плотность диффундирующего газа.
С учетом формулы для длины свободного пробега:
где σ - эффективное сечение молекулы газа, и выражения для средней скорости:
выражение для коэффициента диффузии приобретает вид:
Как следует из этой формулы, коэффициент диффузии растет с повышением температуры: и уменьшается при увеличении концентрации: D ~ 1/n. Уменьшение коэффициента диффузии при увеличении концентрации молекул связано с уменьшением длины свободного пробега λ, что приводит к более частым соударениям диффундирующих частиц с молекулами газа.
Слайд 83. Теплопроводность
При описании теплопроводности в качестве переносимой величины Ω
выступает энергия теплового движения молекулы газа:
где: I - число степеней
свободы молекулы, а температура считается зависящей только от координаты x: T = T(x). Тогда выражение
дает уравнение теплопроводности:
Если учесть соотношение ikn/2 = cVρ, где: cV - удельная теплоемкость газа при постоянном объеме. Учтя, что ρ = mn - плотность газа, то уравнение теплопроводности приобретет вид:
κ = ⅓‹v›λcVρ.
При подстановке в эту формулу выражений для длины свободного пробега и средней скорости имеем:
Слайд 9Из этой формулы следует, что с повышением температуры, коэффициент теплопроводности
тоже увеличивается:
.
Но в отличие от коэффициента диффузии, этот коэффициент не зависит от концентрации молекул газа.Эта особенность связана с тем, что в более плотном газе в теплопроводности участвует большее количество молекул. Но при этом, вследствие меньшей длины свободного пробега λ, энергия передается на меньшие расстояния. Для более разреженного газа ситуация обратная: в переносе энергии участвует меньшее число молекул, но этот перенос осуществляется на большие расстояния.
Независимость теплопроводности от концентрации молекул газа справедлива только в том случае, если в нем отсутствует макроскопическое перемешивание, и перенос энергии осуществляется без переноса вещества.
Слайд 104. Вязкость
Явление вязкости газа может быть описано с помощью
уравнения
при подстановке в него в качестве переносимой величины Ω
импульса молекулы при упорядоченном движении газа в направлении, перпендикулярном оси OX: Ω(x) = mu(x), где: u(x) - скорость течения газа в направлении, перпендикулярном оси OX, в точке с координатой x: u = u(x). С учетом этого уравнение вязкости будет иметь виде: Тогда формула для расчета потока импульса Jp приобретет вид
где коэффициент вязкости η определяется с помощью следующего выражения
η = ⅓‹v›λρ
Слайд 11Величина Jp имеет смысл силы, с которой слои газа, двигающиеся
в направлении, перпендикулярном оси OX, действуют друг на друга.
Температурная зависимость
коэффициента вязкости аналогична зависимости для коэффициента теплопроводности: ,и этот коэффициент, также как и теплопроводность, не зависит от концентрации молекул газа (плотности газа).
Независимость коэффициента вязкости от плотности газа имеет то же объяснение, что и для теплопроводности. С повышением плотности увеличивается число молекул, переносящих импульс, но уменьшаются расстояния, на которые этот перенос осуществляется.
Слайд 13Сравнивая выражения для коэффициентов переноса, получим следующие соотношения между ними:
η = ρD, κ = cVη = cVρD.
Все три коэффициента
(вязкости, теплопроводности и диффузии) зависят от средней длины свободного пробега молекул газа. Поэтому из опытов по диффузии, теплопроводности или вязкости газа можно вычислить ‹λ› и подсчитать эффективное поперечное сечение соударения молекул σ.Слайд 145. Эффузия в разреженном газе
Состояние газа, при котором длина
свободного пробега его молекул λ становится порядка или более характерного
размера сосуда L, в котором находится газ, называется вакуумом.Различают низкий вакуум, при котором λ < L, средний, когда λ ≈ L и высокий (или глубокий), при котором λ >> L.
Отметим, что газ при одной и той же плотности в сосудах разного размера может находиться в обычном состоянии при λ >> L и описываться полученными выше уравнениями переноса, а может представлять собой вакуум при λ > L, для описания которого эти уравнения не применимы. Так в частности воздух при нормальном атмосферном давлении в небольших порах дерева или почвы может находиться в состоянии вакуума, в отличие от того же воздуха в макроскопическом сосуде.
Рассмотрим процесс переноса в разреженном газе. Пусть имеется заполненный разреженным газом сосуд, разделенный перегородкой с небольшим отверстием. Будем считать, что размер отверстия и толщина перегородки много меньше длины свободного пробега молекул газа.
Слайд 15Процесс истечения разреженного газа из отверстия, характерные размеры которого много
меньше длины свободного пробега, называется эффузией.
Если стенки одной части сосуда
поддерживать при температуре T1, а второй - при температуре T2, то плотность потока молекул из первой части сосуда во вторую будета из второй в первую соответственно с помощью выражения
Слайд 16где: ‹v1› и ‹v2› - средние скорости молекул в первой
и во второй частях сосуда, зависящие от температур T1 и
T2, n1 и n2 - соответственно концентрации молекул в этих частях сосуда.Будем считать, что молекулы, движущиеся в отверстии навстречу друг другу, не сталкиваются между собой. Тогда учитывая выражения для средней скорости молекул и зависимости концентрации молекул n от давления P и температуры T для идеального газа, позволяет определить суммарную плотность потока j = j1 – j2 из первой части сосуда во вторую
где: P1 и P2 - давления газа в первой и во второй частях сосуда соответственно.
Эта формула описывает процесс эффузии разреженного газа через маленькое отверстие в перегородке между двумя частями сосуда, газ в которых имеет соответственно температуры T1 и T2 и давления P1 и P2.
Из этой формулы можно получить условие, при котором разреженный газ в двух частях сосуда будет находиться в равновесии. Полагая в формуле плотность потока j = 0, имеем
Слайд 17Если температуры стенок в двух частях рассматриваемого сосуда различны, то
в состоянии равновесия давление разреженного газа в этих частях будет
так же различным. В части сосуда с большей температурой стенок давление газа так же будет большим.Если давления Р1 и Р2 были первоначально одинаковыми, то вследствие эффузии газ начнет перетекать из области с более низкой температурой, в область с более высокой. Это явление называется тепловой эффузией.
Примером природного явления, в котором проявляется тепловая эффузия, может служить процесс выхода воздуха из почвы днем и всасывания его в почву ночью. В дневные часы верхний слой почвы нагревается, и воздух по небольшим порам и отверстиям в почве выходит наружу. В ночные часы, вследствие охлаждения верхнего слоя почвы процесс происходит в обратном направлении.
Для разделения газовых смесей, в частности смесей изотопов, нашло применение явление изотермической эффузии. Это явление заключается в том, что газ из смеси, молекулы которого имеют меньшую массу, более интенсивно проходит через пористую перегородку, чем газ, имеющий более тяжелые молекулы. Изотермическая эффузия нашла применение, в частности, для разделения изотопов урана при его обогащении.
В разреженном газе имеет место радиометрический эффект - отталкивание от нагретой поверхности (пластины) другой, более холодной пластины. Если длина свободного пробега молекул газа сравнима или меньше расстояния между пластинами, то происходит непосредственный перенос импульса молекулами газа от горячей пластины к холодной, что и приводит к появлению силы отталкивания.