Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛЕКЦИЯ 2 Экономика Робинзонады: основные характеристики производства и
Содержание
- 1. ЛЕКЦИЯ 2 Экономика Робинзонады: основные характеристики производства и
- 2. Основные вопросыИсходные условия и суть проблемыПроизводствоФункция полезности и ее свойства
- 3. 1. Исходные условия и суть проблемы
- 4. Общая постановка задачиРобинзон стремится максимизировать степень своего благосостояния («максимизация счастья»)В его распоряжении имеются:Время собственной жизниПриродные ресурсы
- 5. Эффект и издержкиКонкретизация задачи: показать закономерности распределения
- 6. Наличие «размена» между источниками благосостоянияПроизводственная деятельность позволяет
- 7. 2. Производство
- 8. Факторы производства и производственная деятельностьСубъективный фактор производства
- 9. Технология производства и производственная функцияТехнология производства -
- 10. Ограниченные и неограниченные факторы производстваНеограниченный ресурс –
- 11. Граница производственных возможностейx1,…,xn – вектор производимых потребительских
- 12. Графическое представление границы производственных возможностейВремя производства (T)
- 13. 3. Функция полезности и ее свойства
- 14. Проблема измерения полезностиДолгое время считалось, что величина
- 15. Кардиналистская модель оценки полезности Ранг
- 16. Недостатки кардиналистского подходаВозможность точного измерения полезности в
- 17. Ординалистская концепция маржинализмаАвтор – выдающийся итальянский экономист
- 18. Гипотезы в отношении системы индивидуальных преференцийМонотонность (принцип
- 19. Количественное представление системы предпочтений Количественное представление системы
- 20. Свойства функции индивидуальной полезности U(x1, x2)Возрастающий характер - Ui=U/xi>0)Выпуклость вверх Примечание: строгая выпуклость вверх – f(ax+(1-a)y)>af(x)+(1-a)f(y)Дифференцируемость
- 21. Форма кривых безразличия, отвечающая гипотезам в отношении
- 22. Свойство субституцииИз выпуклости функции полезности вытекает свойство
- 23. Построение кривых безразличия на основе функции полезностиПусть
- 24. Скачать презентанцию
Основные вопросыИсходные условия и суть проблемыПроизводствоФункция полезности и ее свойства
Слайды и текст этой презентации
Слайд 1ЛЕКЦИЯ 2
Экономика Робинзонады: основные характеристики производства и потребления
Введение в
общую экономическую теорию
М.В.ЛомоносоваСлайд 4Общая постановка задачи
Робинзон стремится максимизировать степень своего благосостояния («максимизация счастья»)
В
его распоряжении имеются:
Время собственной жизни
Природные ресурсы
Слайд 5Эффект и издержки
Конкретизация задачи: показать закономерности распределения (аллокации) Робинзоном своего
времени между производством необходимых для него потребительских благ и свободным
временем в условиях максимизации уровня благосостоянияЭффект – степень удовлетворения потребностей Робинзона
Издержки (затраты) – жизнь Робинзона (измеряется временем)
Слайд 6Наличие «размена» между источниками благосостояния
Производственная деятельность позволяет Робинзону преобразовывать природные
ресурсы в потребительские блага и тем самым повышать степень своего
благосостоянияСвободное время - время отдыха и развлечений – также является источником благосостояния
Суть «размена» (trade-off): увеличение времени, выделяемого на производственную деятельность, уменьшает время досуга и наоборот
Альтернативные издержки как упущенная выгода от неиспользования времени по другому направлению
Слайд 8Факторы производства и производственная деятельность
Субъективный фактор производства (категория запаса) –
способность человека к труду (рабочая сила). Труд – как функционирующая
рабочая сила (категория потока)Объективный фактор производства (категория запаса) – природные ресурсы (предметы труда)
Производственная деятельность – взаимодействие субъективных и объективных факторов производства, результатом которого является полезное для человека благо
Невозможность выявления роли отдельных факторов в создании продукта
Слайд 9Технология производства и производственная функция
Технология производства - комбинация времени функционирования
рабочей силы и натуральных количеств предметов труда, необходимых для создания
потребительского благаТехнически эффективная технология – технология, по отношению к которой не существует иной технологии, использующей для производства единицы изделия меньшее количество одного фактора производства при том же или меньшем количестве всех иных факторов производства
Производственная функция – множество всех технически эффективных технологий
Математическая структура производственной функции: Qi=f(z1,…, zm), где Qi – величина выпуска i-того блага,
z1,…, zm – количества различных факторов производства, включая рабочую силу. При этом Q / zj > 0
Слайд 10Ограниченные и неограниченные факторы производства
Неограниченный ресурс – такой ресурс, количество
которого не лимитирует выпуск производимого с его использованием продукта
Предположение о
неограниченности всех природных ресурсов означает, что лимитирующим фактором производства является рабочая сила РобинзонаУдельные затраты труда - количество времени, расходуемое на производство одной единицы блага; обратный показатель – производительность труда
В условиях неограниченности природных ресурсов и при заданном уровне производительности труда величина выпуска любого блага становится функцией времени, выделяемого Робинзоном на его производство: Qi=f(L)
Слайд 11Граница производственных возможностей
x1,…,xn – вектор производимых потребительских благ
Граница производственных возможностей
– максимально достижимые при фиксированных количествах факторов производства наборы выпускаемых
товаровПусть природные ресурсы неограниченны, T – дневная продолжительность рабочего времени, ai – удельные затраты труда на производство –i-того блага, i=1,2. Тогда:
T=x1•a1+ x2•a2
x2=T/ a2-(a1/ a2)• x1
Последняя формула определяет границу производственных возможностей Робинзона при рассматриваемых условиях
Коэффициент k=-(a1/ a2) характеризует «размен» между производством второго и первого блага
Слайд 12Графическое представление границы производственных возможностей
Время производства (T) - 8, 6
и 4 часов
Удельные затраты времени: a1=0,1 часа, a2=1,2 часа
Наклон
функции производственных возможностей - показатель «размена» (trade-off) блага 2 на благо 1Слайд 14Проблема измерения полезности
Долгое время считалось, что величина полезности не поддается
квантификации
Маржиналистская революция последней трети XIX века (Менгер, Визер, Бем-Баверк –
в Австрии, Джевонс – в Великобритании) и возникновение кардиналистской концепцииОсобенность кардиналистской концепции:
объективной меры человеческих потребностей нет, но существует соизмеримость субъективная;
потребности любого человека могут быть ранжированы с точки зрения их важности (“еда важнее развлечений”);
ранжированию подлежат и степени удовлетворения одной и той же потребности (с усилением насыщения соответствующей потребности ее значение для индивида снижается) – концепция убывающей предельной полезности
Слайд 15Кардиналистская модель оценки полезности
Ранг
Степень удовлетворения потребности
потребности I II III IV V VI VII VIII IX X
1 10 9 8 7 6 5 4 3 2 1
2 9 8 7 6 5 4 3 2 1 0
3 8 7 6 5 4 3 2 1 0
4 7 6 5 4 3 2 1 0
5 6 5 4 3 2 1 0
6 5 4 3 2 1 0
7 4 3 2 1 0
8 3 2 1 0
9 2 1 0
10 1 0
11 0
Слайд 16Недостатки кардиналистского подхода
Возможность точного измерения полезности в «ютилях» индивидами крайне
сомнительна
Не учитывается влияние на предельную полезность блага наличия других благ
Слайд 17Ординалистская концепция маржинализма
Автор – выдающийся итальянский экономист Парето
Гипотеза о способности
индивида ранжировать имеющиеся наборы благ [x1=(x11, … , x1n), …
, xk=(xk1, … , xkn)], то есть выявлять предпочтения в отношении любых двух наборов xi и xj при помощи одного из трех взаимоисключающих утверждений: набор xi более предпочтителен, чем набор xj (xi xj); набор xi менее предпочтителен, чем набор xj (xi xj ); оба набора равноценны (xi ≈ xj)Кривая безразличия – представляет множество наборов благ, имеющих одинаковую ценность
f
p
Слайд 18Гипотезы в отношении системы индивидуальных преференций
Монотонность (принцип «предпочтения большего меньшему»)
Преференции
являются монотонными в том случае, когда потребитель при сравнении любых
двух наборов x и y таких, что все элементы набора x не меньше по количеству, чем соответствующие элементы набора y (x ≥ y), рассматривает набор x как не менее предпочтительный, чем набор yВыпуклость
Преференции являются выпуклыми, если для любой пары наборов x и y, где набор x является не менее предпочтительным, чем набор y, и для любого числа a из интервала [0,1] ax+(1-a)y ≈ f y
Непрерывность
Для любого набора x и любого наперед заданного числа ε > 0 найдется набор y такой, что |xj- yj |≤ ε
Слайд 19Количественное представление системы предпочтений
Количественное представление системы предпочтений в виде
функции полезности U= U(x1,…,xn) возможно, если xi xj
тогда и только тогда, когда U(xi) > U(xj ).Функция полезности носит индивидуальный характер (невозможность межличностного сопоставления полезностей)
Величина полезности товарного набора рассматривается как индекс, абсолютная величина которого не имеет никакого значения (ординалистская трактовка). Монотонная трансформация этой функции (т.е. функция V(U(x1,…,xn)), такая что dV/dU=F’(U)>0), сохраняет то же самое ранжирование товарных наборов
f
Слайд 20Свойства функции индивидуальной полезности U(x1, x2)
Возрастающий характер - Ui=U/xi>0)
Выпуклость вверх
Примечание:
строгая
выпуклость вверх –
f(ax+(1-a)y)>af(x)+(1-a)f(y)
Дифференцируемость
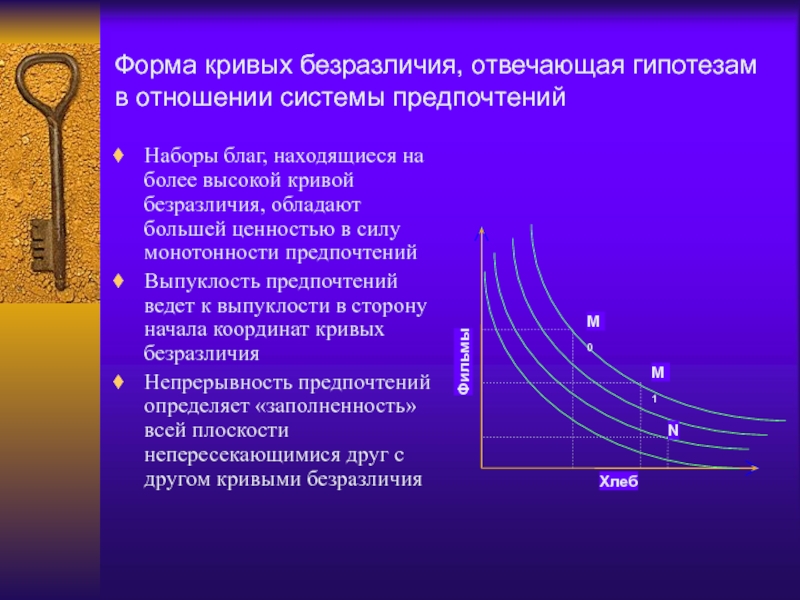
Слайд 21Форма кривых безразличия, отвечающая гипотезам в отношении системы предпочтений
Наборы благ,
находящиеся на более высокой кривой безразличия, обладают большей ценностью в
силу монотонности предпочтенийВыпуклость предпочтений ведет к выпуклости в сторону начала координат кривых безразличия
Непрерывность предпочтений определяет «заполненность» всей плоскости непересекающимися друг с другом кривыми безразличия
Слайд 22Свойство субституции
Из выпуклости функции полезности вытекает свойство субституции (замещения) одних
благ другими: готовность к отказу от потребления одного блага в
случае увеличения количества другогоПредельная норма субституции (замещения) блага x благом y показывает от какого максимального количества блага y потребитель готов отказаться, чтобы получить больше на 1 единицу блага x
В двумерном пространстве (i=1,2)действует принцип убывающей предельной нормы замещения блага по мере роста его потребления: (2xi / xj2)U0> 0, i,j = 1, … ,n, i j.
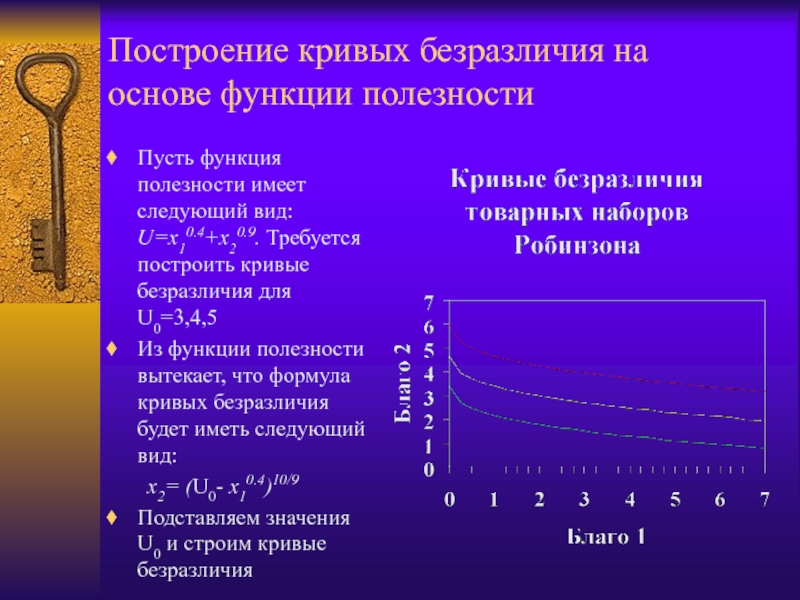
Слайд 23Построение кривых безразличия на основе функции полезности
Пусть функция полезности имеет
следующий вид: U=x10.4+x20.9. Требуется построить кривые безразличия для U0=3,4,5
Из функции
полезности вытекает, что формула кривых безразличия будет иметь следующий вид:x2= (U0- x10.4)10/9
Подставляем значения U0 и строим кривые безразличия