Слайд 1Лекция 4.
Дифракция Фраунгофера
4.1. Дифракция Фраунгофера на длинной и двух
узких щелях. Дифракция от прямоугольного отверстия
4.2. Дифракционная картина вблизи фокуса
линзы Дифракция и оптические приборы
4.3. Дифракционная решетка. Спектральное разложение
4.4. Характеристики решетки как спектрального прибора: дисперсия, разрешающая сила, дисперсионная область
4.5. Закон сохранения энергии в явлениях дифракции
Слайд 24.1. Дифракция Фраунгофера на длинной и двух узких щелях. Дифракция
от прямоугольного отверстия
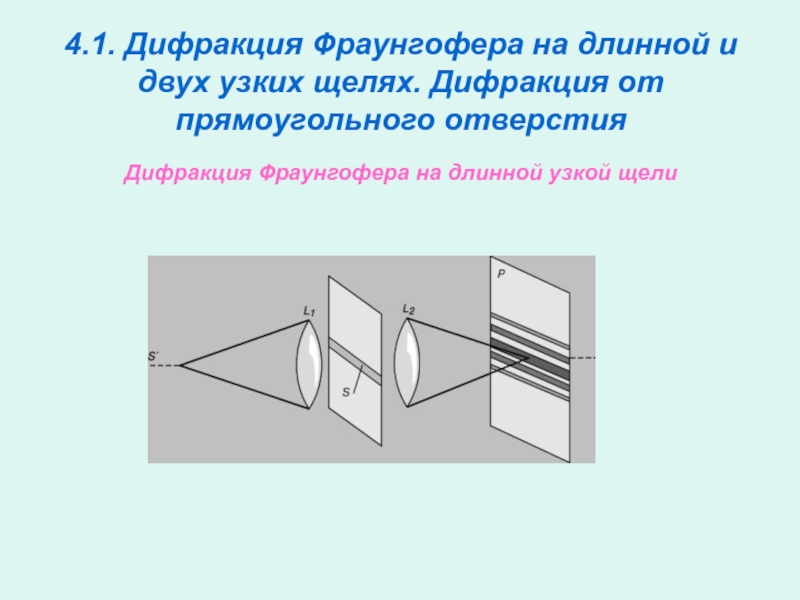
Дифракция Фраунгофера на длинной узкой щели
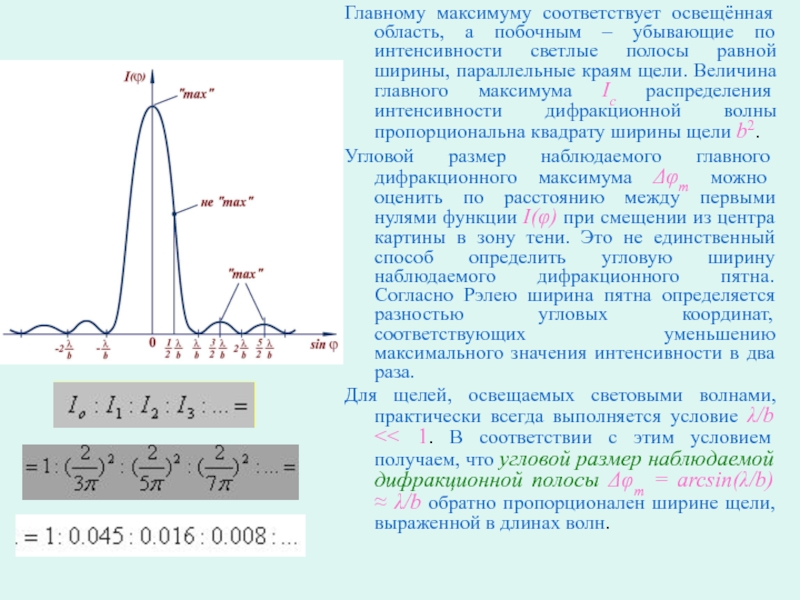
Слайд 4Главному максимуму соответствует освещённая область, а побочным – убывающие по
интенсивности светлые полосы равной ширины, параллельные краям щели. Величина главного
максимума Ic распределения интенсивности дифракционной волны пропорциональна квадрату ширины щели b2.
Угловой размер наблюдаемого главного дифракционного максимума Δφm можно оценить по расстоянию между первыми нулями функции I(φ) при смещении из центра картины в зону тени. Это не единственный способ определить угловую ширину наблюдаемого дифракционного пятна. Согласно Рэлею ширина пятна определяется разностью угловых координат, соответствующих уменьшению максимального значения интенсивности в два раза.
Для щелей, освещаемых световыми волнами, практически всегда выполняется условие λ/b << 1. В соответствии с этим условием получаем, что угловой размер наблюдаемой дифракционной полосы Δφm = arcsin(λ/b) ≈ λ/b обратно пропорционален ширине щели, выраженной в длинах волн.
Слайд 596% мощности светового потока при его дифракции на щели сосредоточено
в пределах телесного угла Δφm.
Если для наблюдения дифракции Фраунгофера используется
линза с фокусным расстоянием f, позволяющая видеть дифракционную картину в её фокальной плоскости на конечном расстоянии от препятствия, то найденному значению угловой ширины дифракционного пятна соответствует его «линейная» ширина Δxm = λf/b.
Отсюда следует, что использование для наблюдения дифракции длиннофокусных линз с большим f позволяет получить на экране визуально различимые светлые и тёмные дифракционные полосы.
Слайд 6Дифракция на двух щелях
Главные минимумы (щели не посылают свет):
Добавочные
минимумы (щели посылают свет, но происходит взаимное гашение когерентных пучков
– деструктивная интерференция):
Главные максимумы (щели посылают свет, происходит взаимное усиление когерентных пучков – конструктивная интерференция):
разность хода пучков 1 и 2.
Рассмотрим экран с двумя щелями, на которые нормально падает плоская монохроматическая волна. Расчеты показывают, что интенсивность света за экраном будет зависеть от угла φ между направлением распространения света и перпендикуляром к экрану.
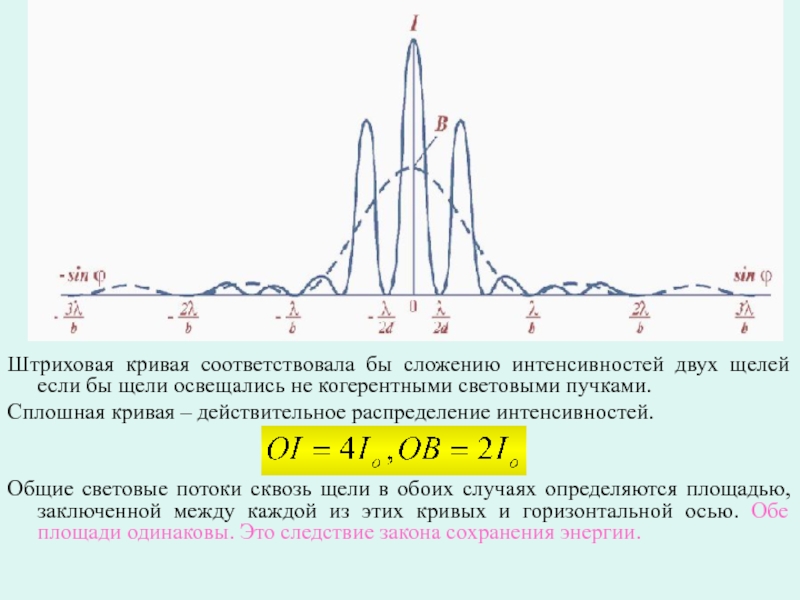
Слайд 7Штриховая кривая соответствовала бы сложению интенсивностей двух щелей если бы
щели освещались не когерентными световыми пучками.
Сплошная кривая – действительное распределение
интенсивностей.
Общие световые потоки сквозь щели в обоих случаях определяются площадью, заключенной между каждой из этих кривых и горизонтальной осью. Обе площади одинаковы. Это следствие закона сохранения энергии.
Слайд 8Дифракция от прямоугольного отверстия
Дифракционный луч характеризуется углами и между направлениями.
где n и m – целые числа, соответствуют минимумам
интенсивности
I0 - интенсивность в центре картины, т.е. ψ = 0, φ = 0.
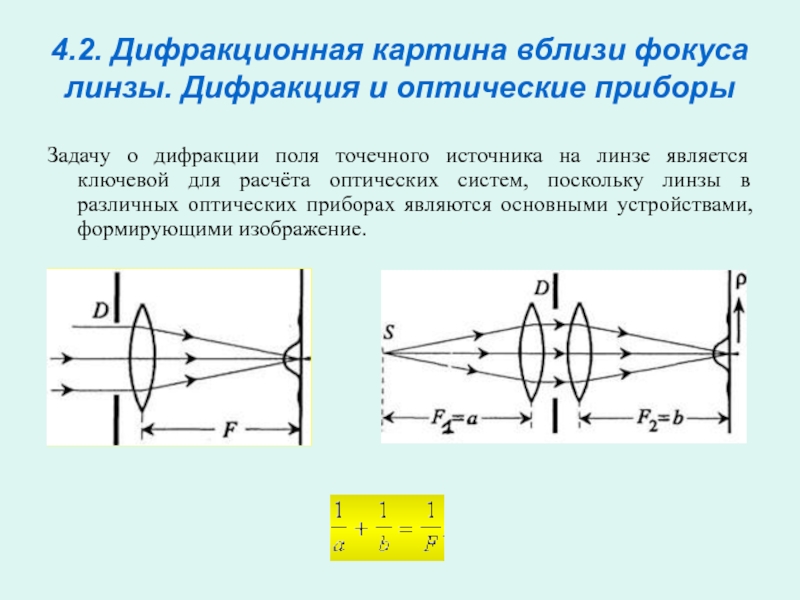
Слайд 94.2. Дифракционная картина вблизи фокуса линзы. Дифракция и оптические приборы
Задачу
о дифракции поля точечного источника на линзе является ключевой для
расчёта оптических систем, поскольку линзы в различных оптических приборах являются основными устройствами, формирующими изображение.
Слайд 10Дифракция Фраунгофера на круглом отверстии
Расчет фраунгоферовой дифракции на круглом
отверстии оказывается достаточно громоздким и приводит к бесселевым функциям первого
порядка J1.
Распределение интенсивности света при дифракции Фраунгофера на круглом отверстии диаметра D выражается формулой
Картина дифракции на круглом отверстии имеет вид
концентрических колец. Центральное светлое
пятно носит название пятна Эйри.
При оценке разрешающей способности оптических
инструментов важно знать размер центрального
дифракционного максимума. Угловой радиус
пятна Эйри выражается соотношением
Слайд 11Интенсивность света в фокусе линзы
Линейный размер дифракционного пятна пропорционален
1/D, а его площадь в фокальной плоскости ~1/D2. При этом
полный поток световой энергии, проходящий через линзу, изменяется пропорционально ее площади (~D2). Таким образом, интенсивность света в фокусе (в центре пятна Эйри) изменяется прямо пропорционально D4. Этот результат можно строго получить методом зон Френеля. Линзу следует рассматривать, как зонную пластинку, которая компенсирует фазовые сдвиги световых колебаний в фокусе как от различных зон Френеля так и от разных элементов одной и той же зоны. На языке векторных диаграмм это означает, что линза «выпрямляет» цепочку элементарных векторов, образующих векторную диаграмму для кольцевых зон Френеля.
Число зон Френеля, укладывающихся на линзе, в случае, когда точка наблюдения совпадает с главным фокусом, равно m = D2/4λF. Вклад одной зоны равен πA0, где A0– амплитуда волны от источника. Пренебрегая закручиванием спирали, то есть считая вклады всех зон одинаковыми, получим A = mπA0. Следовательно, выигрыш от фокусировки
где S – площадь линзы. Из-за малого значения оптической длины волны отношение I/I0 оказывается весьма значительным. Например, для линзы диаметром D = 5 см и фокусным расстоянием F = 50 см выигрыш от фокусировки оказывается порядка 108.

Слайд 12При дифракции Фраунгофера электромагнитной волны на произвольном препятствии, размер которого
равен b, угловой размер области главного максимума дифракционного поля от
препятствия, может быть оценён с помощью формулы φ ~ λ/b.
Дифракционное изображение точечного источника (дифракция на круглом отверстии). В центральное пятно попадает приблизительно 85 % энергии света.
Слайд 13Дифракционный предел разрешения оптических инструментов
Никакая оптическая система не может
дать точечного изображения.
На самом деле изображение точечного предмета оказывается
размытым из-за дифракции. В этом проявляется волновая природа света.
В случае дифракции Фраунгофера на круглом отверстии диаметра D дифракционное изображение состоит из центрального светлого пятна (диск Эйри), и окружающих его светлых и темных колец.
Это дифракционное пятно и принимается за изображение точечного источника. Радиус центрального пятна в фокальной плоскости линзы равен
Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм.
Таким образом существует дифракционный предел качества изображений. Вследствие дифракционного размытия изображения двух близких точек объекта могут оказаться неотличимы от изображения одной точки.
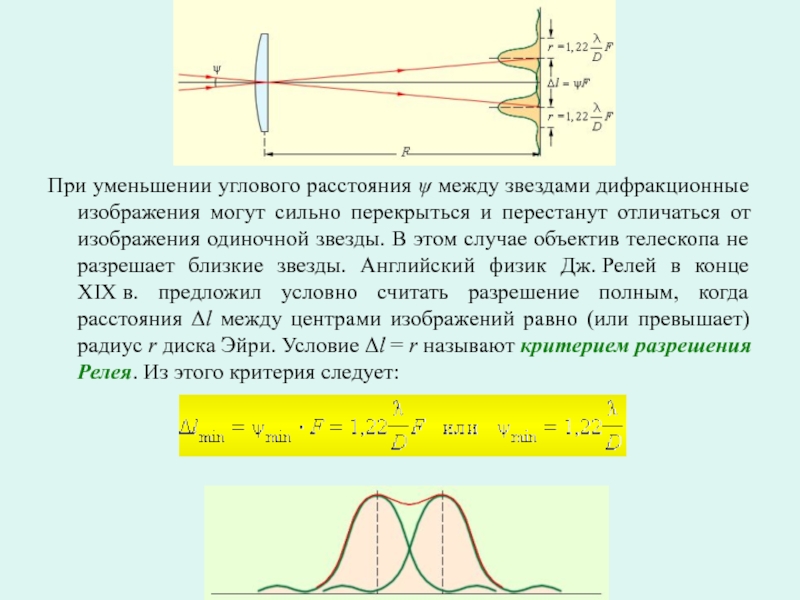
Слайд 14При уменьшении углового расстояния ψ между звездами дифракционные изображения могут
сильно перекрыться и перестанут отличаться от изображения одиночной звезды. В
этом случае объектив телескопа не разрешает близкие звезды. Английский физик Дж. Релей в конце XIX в. предложил условно считать разрешение полным, когда расстояния Δl между центрами изображений равно (или превышает) радиус r диска Эйри. Условие Δl = r называют критерием разрешения Релея. Из этого критерия следует:
Слайд 15Разрешающая способность микроскопа
С помощью микроскопа наблюдают близко расположенные объекты,
поэтому его разрешающаяся способность характеризуется не угловым, а линейным расстоянием
между двумя близкими точками, которые еще могут восприниматься раздельно. Наблюдаемый объект располагается вблизи переднего фокуса объектива. Часто пространство перед объективом заполняется специальной прозрачной жидкостью – иммерсией.
Впервые предел разрешения объектива микроскопа был определен немецким физиком Г. Гельмгольцем (1874 г.). Формула Гельмгольца имеет вид:
здесь λ – длина волны, n – показатель преломления
иммерсионной жидкости, α – так называемый
апертурный угол. Величина nsinα называется числовой апертурой.
У хороших микроскопов апертурный угол α близок к своему
пределу: α ≈ π/2. Как видно из формулы Гельмгольца,
применение иммерсии несколько улучшает предел разрешения.
Полагая для оценок sinα ≈ 1, n ≈ 1,5, получим:
lmin ≈ 0,4λ.
Таким образом, с помощью микроскопа принципиально
невозможно рассмотреть какие-либо детали, размер которых
значительно меньше длины света. Волновые свойства света
определяют предел качества изображения объекта,
полученного с помощью любой оптической системы.

Слайд 164.3. Дифракционная решетка. Спектральное разложение
В состав видимого света входят монохроматические
волны с различными значениями длин волн. Если длины волн от
источника излучения непрерывно заполняют весь диапазон видимого света, то такое излучение называется белым светом. Свет, испускаемый, например, газоразрядными лампами и многими другими источниками, содержит в своем составе отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн. Совокупность монохроматических компонент в излучении называется спектром. Белый свет имеет непрерывный спектр, излучение источников, в которых свет испускается атомами вещества, имеет дискретный спектр. Приборы, с помощью которых исследуются спектры излучения источников, называются спектральными приборами.
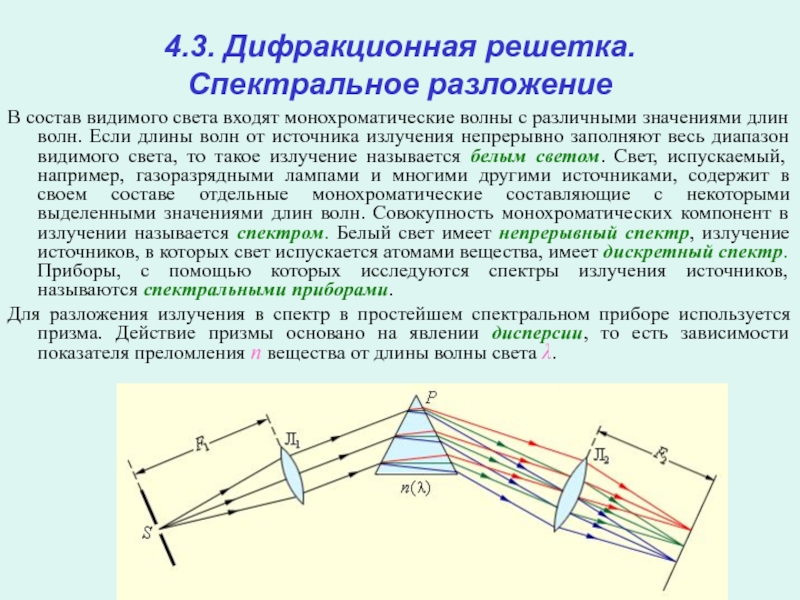
Для разложения излучения в спектр в простейшем спектральном приборе используется призма. Действие призмы основано на явлении дисперсии, то есть зависимости показателя преломления n вещества от длины волны света λ.
Слайд 17В спектральных приборах высокого класса вместо призм применяются дифракционные решетки.
Решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на
поверхности стеклянной или металлической пластинки. У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий.
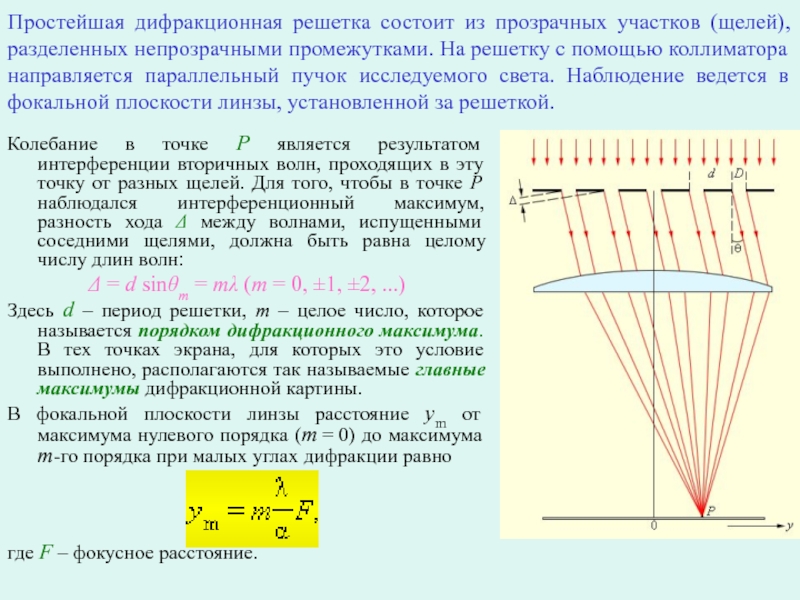
Слайд 18Простейшая дифракционная решетка состоит из прозрачных участков (щелей), разделенных непрозрачными
промежутками. На решетку с помощью коллиматора направляется параллельный пучок исследуемого
света. Наблюдение ведется в фокальной плоскости линзы, установленной за решеткой.
Колебание в точке P является результатом интерференции вторичных волн, проходящих в эту точку от разных щелей. Для того, чтобы в точке P наблюдался интерференционный максимум, разность хода Δ между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн:
Δ = d sinθm = mλ (m = 0, ±1, ±2, ...)
Здесь d – период решетки, m – целое число, которое называется порядком дифракционного максимума. В тех точках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины.
В фокальной плоскости линзы расстояние ym от максимума нулевого порядка (m = 0) до максимума m-го порядка при малых углах дифракции равно
где F – фокусное расстояние.
Слайд 19Следует обратить внимание на то, что в каждой точке фокальной
плоскости линзы происходит интерференция N волн, приходящих в эту точку
от N щелей решетки. Это так называемая многоволновая (или «многолучевая») интерференция. Распределение световой энергии в плоскости наблюдения резко отличается от того, которое наблюдается в обычных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, потому амплитуда колебаний возрастает в N раз, а интенсивность в N2 раз по сравнению с колебанием, которое возбуждает волна только от одной щели.
При смещении из главных максимумов интенсивность колебаний быстро спадает. Чтобы N волн погасили друг друга, разность фаз должна измениться на 2π/N, а не на π, как при интерференции двух волн. На рисунке изображена векторная диаграмма колебаний, возбуждаемых волнами от всех N щелей при условии, что сдвиг фаз волн от соседних щелей равен 2π/N, а соответствующая разность хода равна λ/N. Вектора, изображающие N колебаний, образуют в этом случае замкнутый многоугольник. Таким образом, при переходе из главного максимума в соседний минимум разность хода Δ = dsinθ должна измениться на λ/N. Из этого условия можно оценить угловую полуширину δθ главных максимумов: δΔ = δ(dsinθ) = (dcosθ)δθ ≈ dδθ = λ/N δθ = λ/dN.
dN – полный размер решетки. Это соотношение находится в полном согласии с
теорией дифракции в параллельных лучах, согласно которой дифракционная
расходимость параллельного пучка
лучей равна отношению длины
волны λ к поперечному размеру
препятствия.

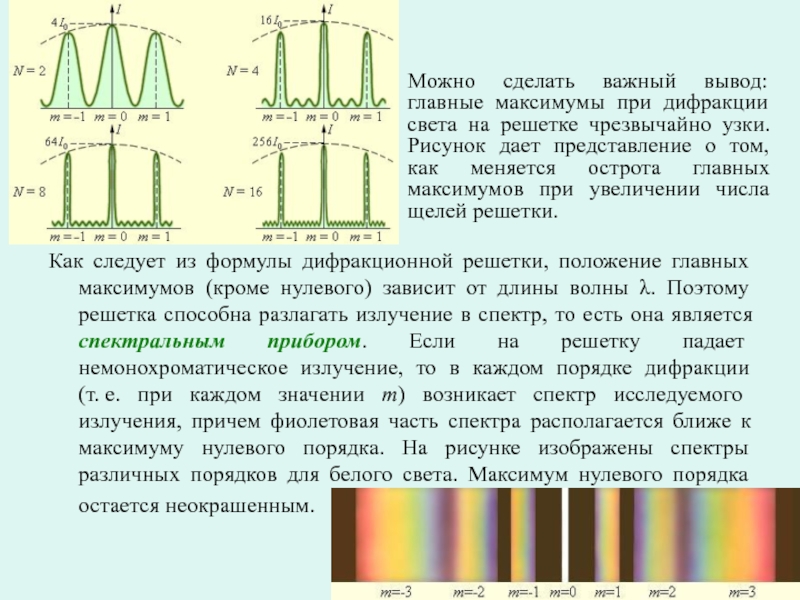
Слайд 20Как следует из формулы дифракционной решетки, положение главных максимумов (кроме
нулевого) зависит от длины волны λ. Поэтому решетка способна разлагать
излучение в спектр, то есть она является спектральным прибором. Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (т. е. при каждом значении m) возникает спектр исследуемого излучения, причем фиолетовая часть спектра располагается ближе к максимуму нулевого порядка. На рисунке изображены спектры различных порядков для белого света. Максимум нулевого порядка остается неокрашенным.
Можно сделать важный вывод: главные максимумы при дифракции света на решетке чрезвычайно узки. Рисунок дает представление о том, как меняется острота главных максимумов при увеличении числа щелей решетки.
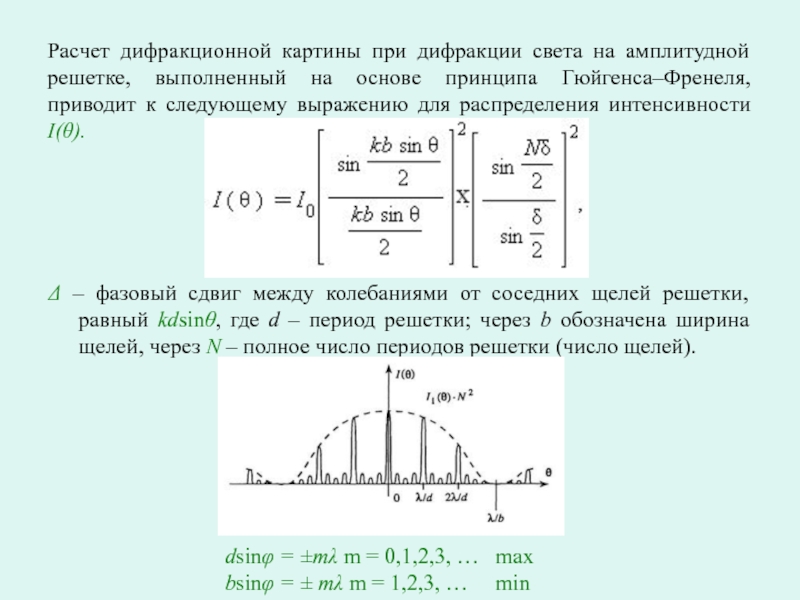
Слайд 21Расчет дифракционной картины при дифракции света на амплитудной решетке, выполненный
на основе принципа Гюйгенса–Френеля, приводит к следующему выражению для распределения
интенсивности I(θ).
Δ – фазовый сдвиг между колебаниями от соседних щелей решетки, равный kdsinθ, где d – период решетки; через b обозначена ширина щелей, через N – полное число периодов решетки (число щелей).
dsinφ = ±mλ m = 0,1,2,3, … max
bsinφ = ± mλ m = 1,2,3, … min
Слайд 224.4. Характеристики решетки как спектрального прибора: дисперсия, разрешающая сила, дисперсионная
область
Положение узких главных максимумов зависит от длины волны λ. Это
позволяет использовать решетку в качестве спектрального прибора. Решетка способна разлагать свет в спектр. Для этого могут быть использованы дифракционные максимумы различных порядков (кроме m = 0). Практически, однако, используются главные максимумы, расположенные в пределах основного лепестка диаграммы излучения одиночной щели, имеющего полуширину λ/b. Отсюда можно получить оценку: mmax ≤ d/b.
Обычно спектрографы с дифракционной решеткой работают при m = 1 или 2, очень редко при m = 3. Качество решетки как спектрального прибора может быть охарактеризовано рядом параметров. К ним относятся угловая дисперсия, дисперсионная область и разрешающая способность.
Слайд 23Угловая дисперсия
Угловой дисперсией спектральных приборов принято называть величину Dθ
= dθ/dλ. Используем уравнение dsinθ = mλ
В случае решетки, угловая
дисперсия равна
Приближенное выражение m/d справедливо в случае малых дифракционных углов.
Дисперсионная область
Если спектры соседних порядков перекрываются, то спектральный прибор становится непригодным для исследования соответствующих участков спектра. Максимальная ширина спектрального интервала Δλ, при которой еще не происходит перекрытия спектров, называется дисперсионной областью спектрального прибора.
Для случая решетки следует: Δλ = λ/m.
В дифракционных решетках используются спектры низких порядков. Поэтому решетки пригодны для исследования широких участков спектра.
Слайд 24Найдём угловую ширину m дифракционного максимума m-го порядка. Очевидно, m
определяется двумя ближайшими минимумами min–(m), min+(m) к направлению дифракционного максимума
m-го порядка:
m = min+(m) – min–(m).
Направления min–(m), min+(m) определяются из условия образования замкнутой кривой, суммой комплексных амплитуд от всех щелей:
sinm = k/Nd,
где k - принимает все целые значения кроме 0, N, 2N, 3N,…
С учётом того, что ближайшие к m-ому максимуму нули соответствуют значениям k = 1, получаем: m = arcsin[(m + 1/N)/d] – arcsin[(m – 1/N)/d].
При большом числе щелей m >> 1, с помощью дифференцирования находим:
m (2/Nd)/[1 – (m/d)]1/2.
В частности, для центрального максимума m = 0, имеем
m (2/Nd).
Эта формула находится в согласии с общими закономерностями фраунгоферовой дифракции. Как видно из нее, угловая полуширина главного максимума определяется длиной волны и общим размером решетки L = Nd.
Угловая ширина дифракционных максимумов обратно пропорциональна ширине решётки L = Nd и с увеличением m становится все больше. Увеличение связано с тем, что для больших значений m уменьшается эквивалентная ширина дифракционной решётки Lэкв, которая представляет собой проекцию дифракционной решётки на направление, перпендикулярное направлению m-ого дифракционного максимума.

Слайд 25Разрешающая способность
Разрешающей способностью спектрального прибора принято называть отношение R
= λ/δλ, где δλ – минимальный интервал между двумя близкими
спектральными линиями, при котором они могут быть разрешены, то есть отделены одна от другой. В качестве критерия разрешения используется обычно критерий разрешения Рэлея. Спектральные линии с близкими значениями λ и λ + δλ считаются разрешенными, если главный максимум дифракционной картины для одной спектральной линии совпадает по своему положению с первым дифракционным минимумом для другой спектральной линии. Рисунок поясняет критерий Рэлея.
Так как спектральные линии, некогерентны, результирующая интенсивность равна сумме интенсивностей (сплошная кривая на рис.). Наличие провала в центре кривой распределения интенсивности указывает на условный характер критерия Рэлея.
Для разрешающей способности дифракционной решетки это:
dsinθ = mλ dδθcosθ = mδλ
δθ = (mδλ)/(dcosθ) ≈ mδλ/d
λ/Nd = mδλ/d или
R = λ/δλ = mN
Слайд 264.5. Закон сохранения энергии в явлениях дифракции
Теория электромагнитного излучения противоречит
закону сохранения энергии. Периодическое исчезновение электромагнитной волны на графике говорит
о том, что в отдельных точках энергия электромагнитной волны исчезает, потом вновь появляется.
Из графика 9 видно, что существует две точки за период, равный длине волны, в которых масса и энергия волны становится равна 0. Внятного описания, где в этот момент находится масса и энергия электромагнитного излучения, теория не дает.
Если энергия электромагнитной волны в эти моменты исчезает, то это противоречит закону сохранения
энергии. Если в эти моменты энергия
физических полей и сохраняется в
другом виде, то теория обязана
ответить на вопрос - в каком именно
виде она сохраняется. Этого ответа
в ней нет. Противоречие электромагнитной
теории закону сохранения энергии говорит
о её не корректности.
В чем ошибка этих рассуждений?