Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4. Транспортная задача ЛП.Экономические задачи, сводящиеся к
Содержание
- 1. Лекция 4. Транспортная задача ЛП.Экономические задачи, сводящиеся к
- 2. План:1.Постановка транспортной задачи. Экономико-математическая модель. Пример ТЗ.
- 3. Транспортная задача линейного программированияЗаданы m источников ресурса
- 4. Таблица транспортной задачи
- 5. Экономико-математическая модель
- 6. Пример (1) транспортной задачиИмеется три поставщика и
- 7. Найти объёмы перевозок для каждой пары «поставщик-потребитель»,
- 8. Ограничения ТЗX11+X21+X31=20X12+X22+X32= 110X13+X23+X33= 40X14+X24+X34= 110 Потребности удовлетворены.Xij≥0F(X)=
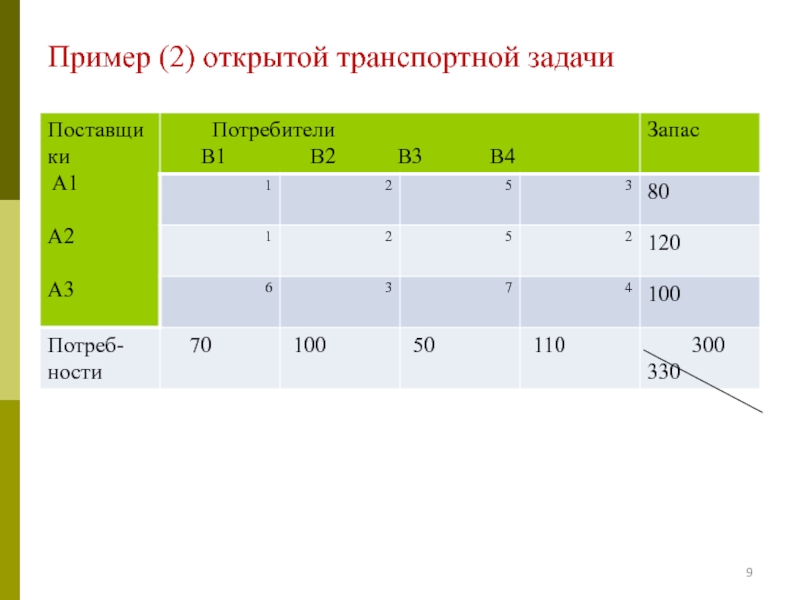
- 9. Пример (2) открытой транспортной задачи
- 10. ai< bj , ТЗ открытого типа Сведём к задаче закрытого типа:
- 11. I этап: Составление первоначального опорного плана1. Метод
- 12. II этап: Улучшение плана перевозок методом потенциаловui
- 13. 1)Проверка условия балансаТЗ является закрытой, если:Если ТЗ является открытой, необходимо ввести фиктивного поставщика или потребителя.
- 14. Пример решения ТЗ
- 15. ЭММ транспортной задачи
- 16. 1А. Определение начального опорного плана методом северо-западного
- 17. 1Б. Метод наименьших элементовk=m+n-1 7=7 – решение невырожденное f(x)=2*80+1*40+2*20+2*60+1*50+4*50+0*30=610
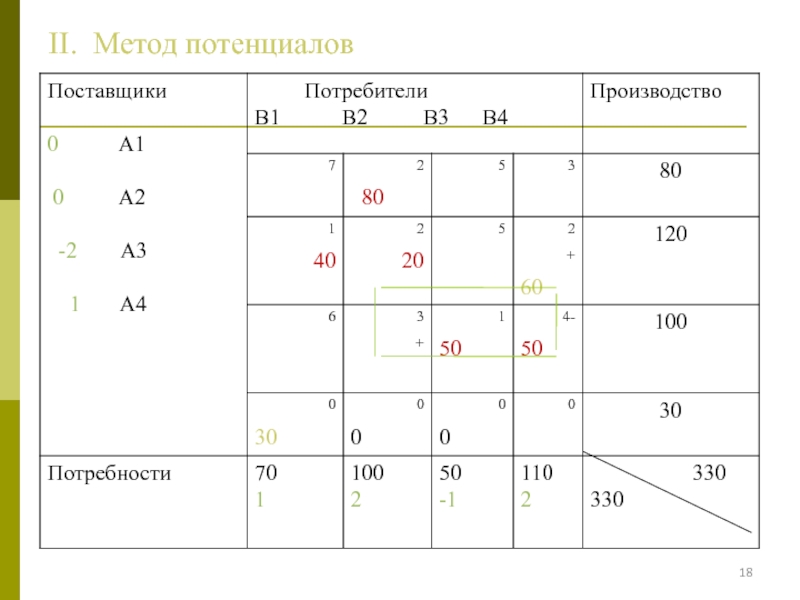
- 18. II. Метод потенциалов
- 19. 2 этап. Применение метода потенциаловДля базисных переменных: vj –ui=cij
- 20. Метод потенциаловвыполняться условие:Для небазисных переменных должно
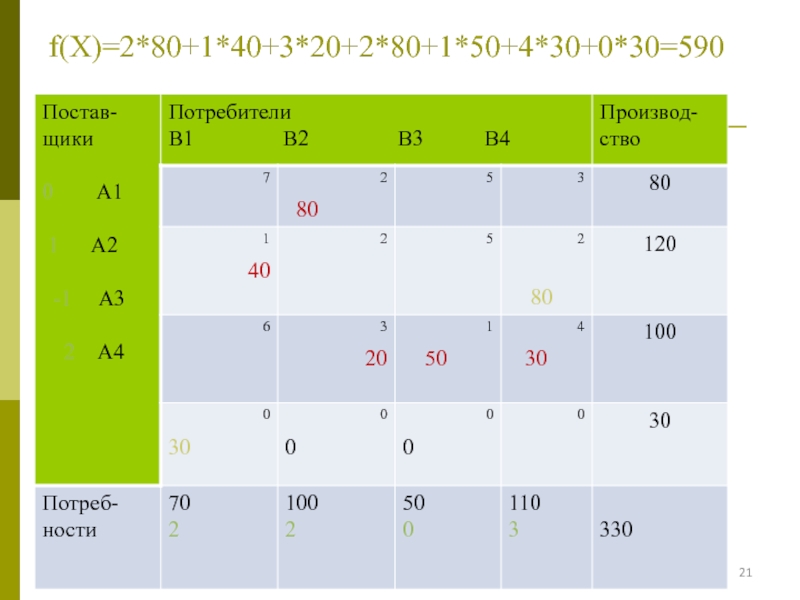
- 21. f(Х)=2*80+1*40+3*20+2*80+1*50+4*30+0*30=590
- 22. План задачи:
- 23. Оптимизационные задачи, сводящиеся к транспортным моделям1.Многопродуктовая транспортная
- 24. 1.Многопродуктовая транспортная модель Организация перевозок в
- 25. Верхний индекс h соответствует типу груза.Получили m*К
- 26. 2. Транспортная модель с промежуточными пунктами.
- 27. 1) m=3; n=2 Транзитная перевозка через собственные пункты отправления и назначения
- 28. Запись транспортной модели как задачи с транзитными перевозками
- 29. 3.Модель производства с запасами.Рассматривается производство, в рамках
- 30. Модель производства с запасамиPi –затраты на производство
- 31. Модель производства с запасами. Аналогия с транспортной задачей
- 32. Модель производства с запасамиCij =pi ,если i=j,
- 33. 4. Оптимальное распределение оборудованияОборудование m различных видов
- 34. Оптимальное распределение оборудования
- 35. 5.Формирование оптимального штата фирмыФирма набирает штат сотрудников.
- 36. Формирование оптимального штата фирмы
- 37. Скачать презентанцию
План:1.Постановка транспортной задачи. Экономико-математическая модель. Пример ТЗ. 2. Методы нахождения начального опорного плана.3. Метод потенциалов.4. Оптимизационные задачи, сводящиеся к транспортным моделям.
Слайды и текст этой презентации
Слайд 1Лекция 4. Транспортная задача ЛП.Экономические задачи, сводящиеся к транспортной.
Денисова С.Т.
Старший
преподаватель
Слайд 2План:
1.Постановка транспортной задачи. Экономико-математическая модель. Пример ТЗ.
2. Методы нахождения
начального опорного плана.
3. Метод потенциалов.
4. Оптимизационные задачи, сводящиеся к транспортным
моделям.Слайд 3Транспортная задача линейного программирования
Заданы m источников ресурса и
n пунктов
потребления.
ai – запасы в пунктах отправления, i=1,2,..m
bj – потребности в
грузах, j=1,2..nСтоимость транспортировки единицы груза от i-го источника к j-му потребителю равна сij
xij - количество груза, транспортируемого от
от i-го поставщика к j-му потребителю. Определить xij , при которых общие транспортные расходы будут минимальными.
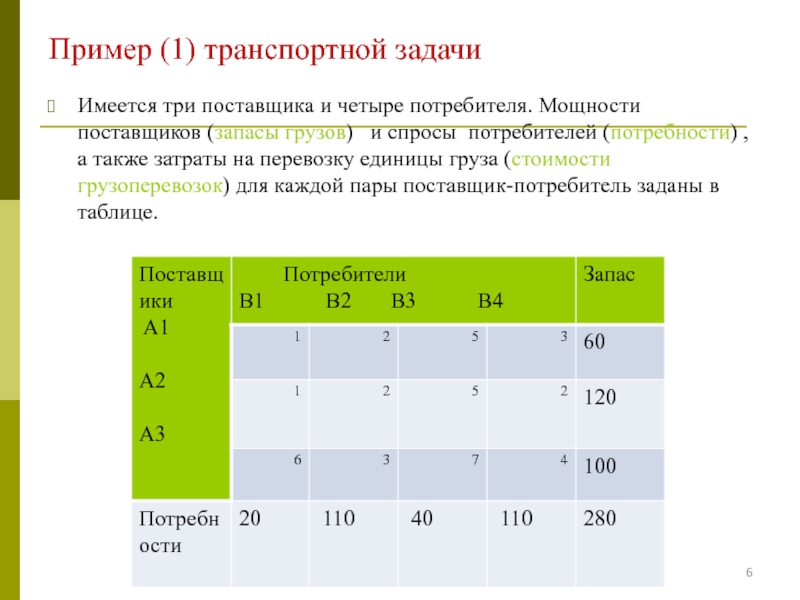
Слайд 6Пример (1) транспортной задачи
Имеется три поставщика и четыре потребителя. Мощности
поставщиков (запасы грузов) и спросы потребителей (потребности) , а
также затраты на перевозку единицы груза (стоимости грузоперевозок) для каждой пары поставщик-потребитель заданы в таблице.Слайд 7Найти объёмы перевозок для каждой пары «поставщик-потребитель», чтобы:
1. мощности поставщиков
были реализованы;
2. спросы всех потребителей были удовлетворены;
3. суммарные затраты на
перевозку были бы минимальны.X11+X12+X13+X14=60
X21+X22+X23+X24= 120
X31+X32+X33+X34= 100 Мощности поставщиков реализованы
Слайд 8Ограничения ТЗ
X11+X21+X31=20
X12+X22+X32= 110
X13+X23+X33= 40
X14+X24+X34= 110 Потребности удовлетворены.
Xij≥0
F(X)= X11+2 X12+5 X13
+3 X14+ X21 +6 X22 +5 X23 +2 X24 +6
X31 +3 X32 +7 X33+4X34min (суммарные затраты на перевозку)Трансп. задача закрытого типа, т.к. ai= bj=280
Слайд 11I этап: Составление первоначального опорного плана
1. Метод северо-западного угла
x11
= min (a1 , b1 ), x12 = min (a1
- x11 , b2 ), если x11 = b1 ,Или x21 = min (b1 - x11 , a2 ), если x11 = a1 и т.д.
2. Метод минимального элемента
сlk = min (cij), где i=1,2,..m, j=1,2,..n
xlk = min (al , bk ),
Слайд 12II этап: Улучшение плана перевозок методом потенциалов
ui - потенциалы строк,
i=1,2,..m
vj - потенциалы столбцов, j=1,2,..n
Для базисных переменных: vj-ui=cij
для небазисных переменных:
vj -ui ≤ cijСлайд 131)Проверка условия баланса
ТЗ является закрытой, если:
Если ТЗ является открытой, необходимо
ввести фиктивного поставщика или потребителя.
Слайд 161А. Определение начального опорного плана
методом северо-западного угла
k=m+n-1
7=7 – решение невырожденное f(x)=7*70+2*10+2*90+5*30+1*20+4*80+0*30=1180
Слайд 171Б. Метод наименьших элементов
k=m+n-1 7=7 –
решение невырожденное f(x)=2*80+1*40+2*20+2*60+1*50+4*50+0*30=610
Слайд 23Оптимизационные задачи, сводящиеся к транспортным моделям
1.Многопродуктовая транспортная модель.
2. Транспортная модель
с промежуточными пунктами.
3.Модель производства с запасами.
4.Оптимальное распределение оборудования.
5.Формирование оптимального штата
фирмы.Слайд 24
1.Многопродуктовая транспортная модель
Организация перевозок в условиях, когда запасами пунктов отправления
являются разнотипные грузы, которые развозятся по пунктам назначения в соответствии
с заявками.К типов груза, для каждого типа груза заданы тарифы перевозок.
Если перевозки разнотипных грузов независимы, то многопродуктовая задача фактически расщепляется на К независимых транспортных моделей.
Чтобы свести многопродуктовую ТЗ к стандартной транспортной модели , будем рассматривать каждый пункт отправления Ai (i=1,2,..m), как К пунктов отправления Aih , (h=1,2,..К), и каждый пункт назначения Bj (j=1,2,..n) как К пунктов назначения Bjh .
Слайд 25Верхний индекс h соответствует типу груза.
Получили m*К – пунктов отправления
и n*К – пунктов назначения. Если между пунктами Aih и
Bjhгруз не перевозится, то этим перевозкам присваивается очень большая стоимость M.
Пример. Даны m =4 пункта отправления Ai (i=1,..4),
в которых содержится до К=3 типов груза, отправляемых в n=2 пункта назначения Bj (j=1,2)
Запасы: а11=200, а13=150, а21=75, а22=100, а23=50, а31=50, а32=100, а41=40, а42=30, а43=50.
Заявки:b11=250, b12=130, b13=150, b21=115, b22=100, b23=100.
Слайд 26
2. Транспортная модель с промежуточными пунктами.
Промежуточные пункты – это дополнительные
площадки, используемые для перегруппировки или хранения груза.
1) Промежуточные пункты
– только пункты отправления и назначения, т.е. груз можно перевозить через любой другой пункт отправления или назначения, пока груз не будет доставлен по назначению.2) Промежуточными пунктами являются только дополнительные пункты.
3) Промежуточными пунктами являются как дополнительные пункты, так и пункты отправления и назначения.
Слайд 293.Модель производства с запасами.
Рассматривается производство, в рамках которого в течение
M периодов (месяцев, недель, дней или иных периодов) планируется выпускать
продукцию в объёмах, равных a1, a2,… aM соответственно. Величина спроса для каждого периода составляет b1,b2,.. bM . Объёмы производства ai и спроса bi могут не совпадать между собой.Спрос на продукцию пр-ва в текущем периоде i может быть удовлетворен:
При реализации продукции, произведённой в текущем периоде i;
При производстве продукции в предыдущие периоды j, j
период i.
Слайд 30Модель производства с запасами
Pi –затраты на производство единицы готовой продукции
в течение периода i;
Si - затраты на хранение единицы
готовой продукции в течение периода i; Задержка в поставке единицы продукции в период i приводит к издержкам, равным ri .
Необходимо составить такой план поставок продукции потребителю, чтобы суммарные затраты f, связанные с производством, хранением и издержками, были минимальны. Обозначим:
Xij – кол-во продукции, изготовляемой в период i и поставляемой в период j.
Слайд 32Модель производства с запасами
Cij =pi ,если i=j, т.е. если продукция
изготовлена и реализуется в период i;
Cij=pi +
,если iСлайд 334. Оптимальное распределение оборудования
Оборудование m различных видов нужно распределить между
n рабочими участками. Производительность единицы оборудования i-го вида на j-м
рабочем участке равна pij , i=1,..m;J=1,..n. Запас оборудования i-го вида равен aI ,
Потребность j-го участка в оборудовании составляет bj . Найти распределение оборудования по рабочим участкам, при котором суммарная производительность максимальна.
Xij – число единиц оборудования i-го вида , выделенное на j-й рабочий участок.
Слайд 355.Формирование оптимального штата фирмы
Фирма набирает штат сотрудников. Она располагает n
группами различных должностей по bj , j=1,..n, вакантных единиц в
каждой группе. По результатам тестирования кандидатов разделяют на m групп поaI кандидатов в каждой группе, i=1,..m. Для каждого кандидата из i-ой группы требуются определённые затраты cIj на обучение для занятия j-й должности.
cIj=0, кандидат полностью соответствует должности,
cIj=∞, кандидат не может занять данную должность.
Требуется распределить кандидатов на должности, затратив минимальные средства на их обучение.