Лекция 5

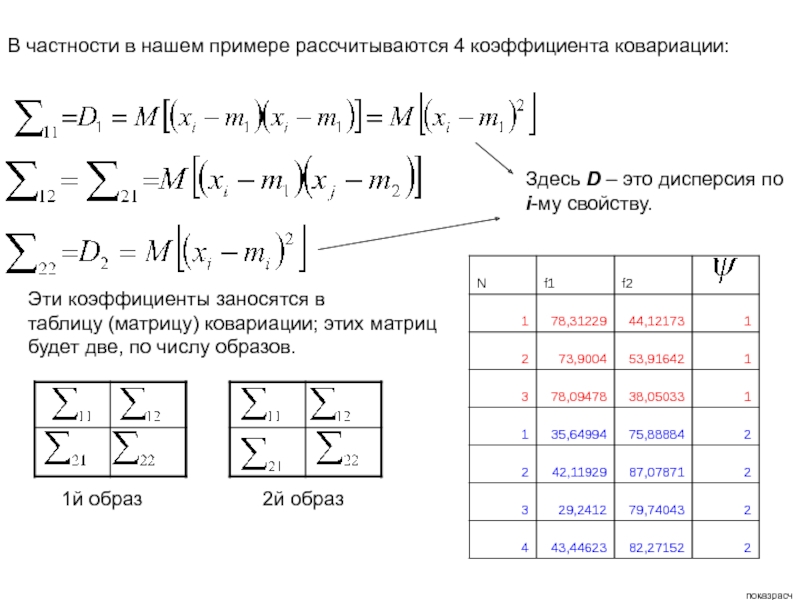
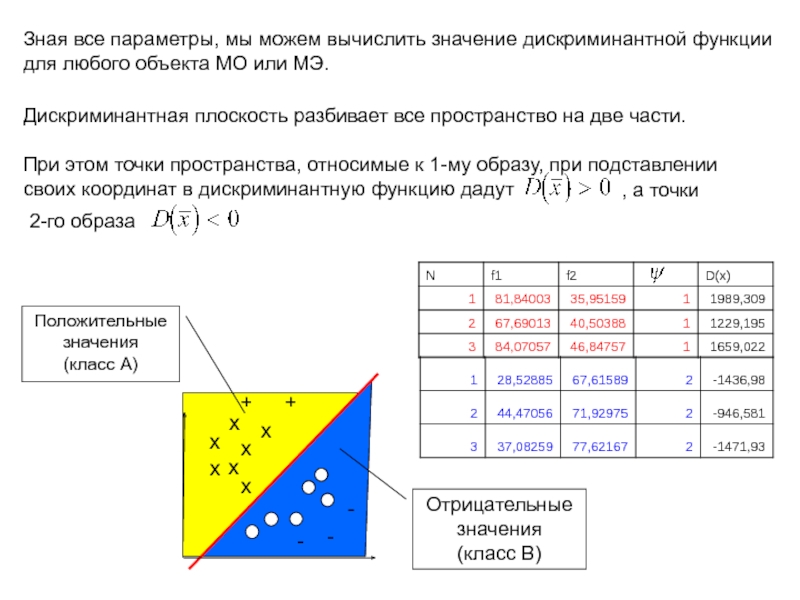
в материале обучения;

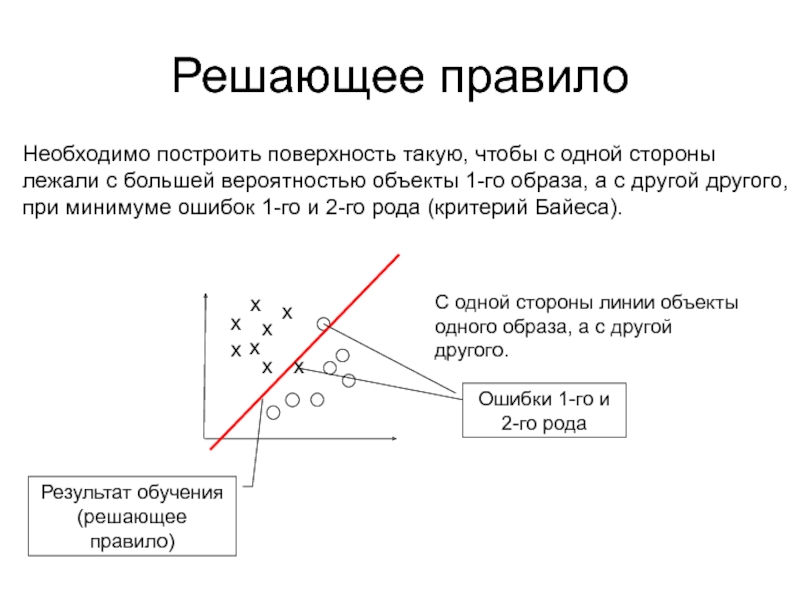
В пространстве «объекты-свойства» объекты обучения имеют

Дискриминантный анализ эффективно использовать при достаточно
близком расположении образов и даже при небольшом их наложении.

всех образов. Для каждого объекта указана его

принадлежность к образу.

с большей вероятностью объекты 1-го образа, а с другой другого,
при

х

х

х

х

х

х

х

С одной стороны линии объекты
одного образа, а с другой
другого.

х

Результат обучения (решающее правило)

образа.
Оказывается, что при равных ковариационных матрицах поверхностью, с одной

, n — размерность пространства.

Уравнение гиперплоскости в общем виде можно записать следующим образом:

Что в привычном двумерном (2 свойства) случае можно представить так:

называется уравнением линейной дискриминантной функции, где
-- n-мерный вектор столбец в

Пример ТОС (2 свойства,
2 образа)
вектор x для 1-го объекта:

(среднее) объектов 2-го образа (вектор);
— транспонирование;
— обратная матрица коэффициентов ковариации.
1е

2е свойство

1е свойство

2е свойство

от того, что в квадратных скобках
, где n - количество

где — математическое ожидание по к-ому свойству.

Коэффициенты ковариации рассчитываются для всех пар свойств
отдельно для объектов 1-го и 2-го образов.

заносятся в
таблицу (матрицу) ковариации; этих матриц
будет две, по числу

Здесь D – это дисперсия по
i-му свойству.

1й образ

2й образ

показрасч

объектов 1-го образа
количество объектов 2-го образа
Обратная матрица к усредненной, обозначается
и

примвыш

объекта МО или МЭ.
х
х
х
х
х
х
х
+
-
-
-
+
Положительные значения
(класс А)
Отрицательные значения
(класс В)

неизвестные. Подробнее как это сделать в Excel
вы рассмотрите на семинарах.

этих образов). Тогда можно построить
линейную дискриминантную функцию для любой

где

образы.

или к области отказа, если
такового

В область отказа попадают такие точки, для которых невозможно
определить принадлежность к одному из образов. Другими словами
точка отказа — это такая точка, координаты которой при
подставлении в дискриминантную функцию дают следующие значения:

;

;

(в соответствии с картинкой внизу)

область отказа