Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 5-6. 22,27.02.14
Содержание
- 1. Лекция 5-6. 22,27.02.14
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Характеристики популяций
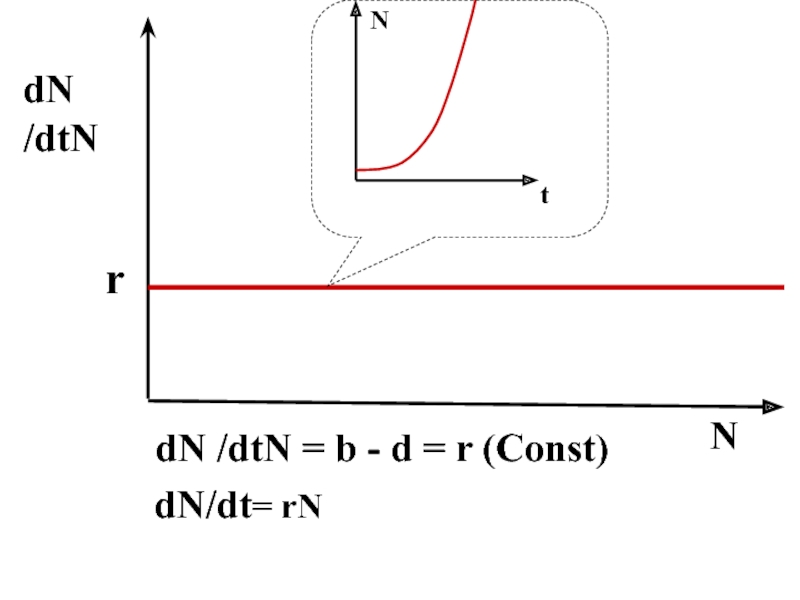
- 7. NtNdN /dtN = b - d = r (Const) dN/dt= rNrdN /dtN
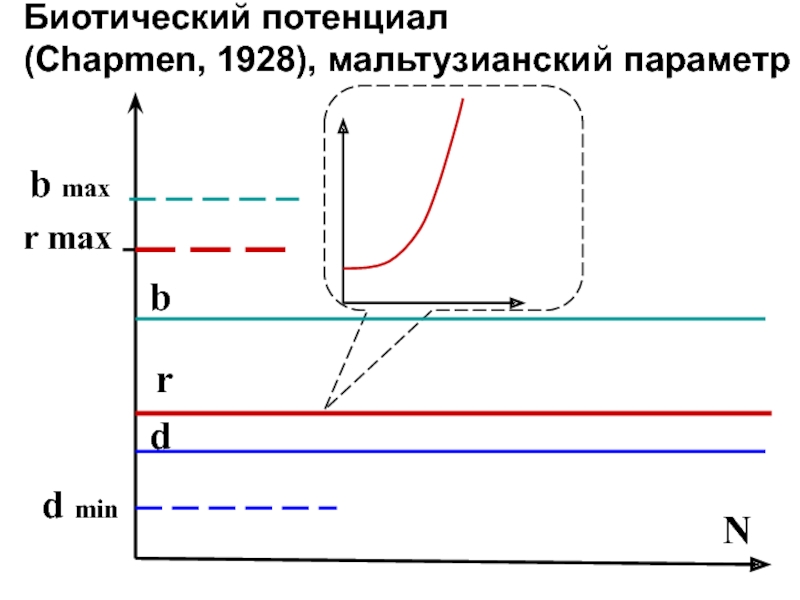
- 8. Nrdbr maxБиотический потенциал (Chapmen, 1928), мальтузианский параметрd minb max
- 9. Ещё одно важное обстоятельство, касающееся экспоненциального роста:
- 10. NdN /dtN = (-r/K)N + r =
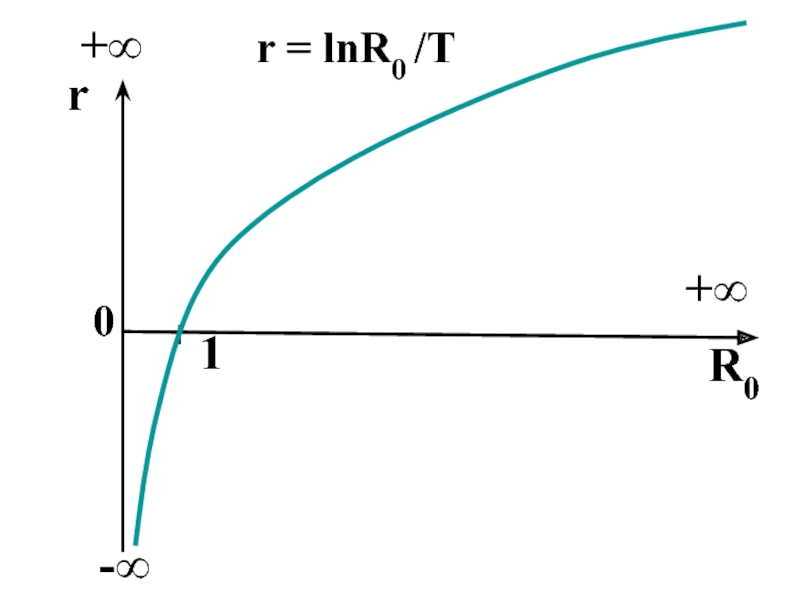
- 11. R0r10r = lnR0 /T+∞+∞-∞
- 12. Приближённый способ расчета удельной скорости роста численности
- 13. Кому давать орден «Мать-героиня»?Из лекций А.М. Гилярова
- 14. Популяция, где по пять детей у молодых
- 15. r1 = (ln 2.5) / 20 =
- 16. ОСНОВНЫЕ УРАВНЕНИЯ (ЛОГИСТИЧЕСКИЙ РОСТ)Логистический (S-образный, сигмоидный)рост замкнутой
- 17. Слайд 17
- 18. S – образный, близкий к логистическому, рост
- 19. Слайд 19
- 20. Слайд 20
- 21. Модель логистического ростане более, чем одна из множества моделей, описывающих S-образный рост
- 22. (A to C) (Left) The relationships between
- 23. Где θ – показатель, характеризующий форму зависимости удельной скорости популяционного роста r0 от плотности
- 24. Разные формы зависимости удельной скорости популяционного роста
- 25. Значения показателя тета для четырех таксономических группа
- 26. На 1780 сериях наблюдений (млекопитающие, птицы, рыбы,
- 27. Монотонно затухающиеЗатухающиеСлучайные колебанияПредельные циклывремяNNt+1= Nt R / (1+a*Ntc)Rc
- 28. СТРАТЕГИИ ПОПУЛЯЦИИ (McArthur, 1967)r-стратегия К-стратегия «отбор на
- 29. Jack of all trades, master of none
- 30. A trade-off (or tradeoff) is a situation that involves losing
- 31. Слайд 31
- 32. времяNr-стратегияЗаселениенеблагоприятной нишиК-стратегия
- 33. жизненные стратегии растений (по Л.Г.Раменскому)Виоленты (силовики) –
- 34. Сравнительная характеристика типов стратегий растений
- 35. «Треугольник» Дж. Грайма
- 36. Эффект “bottleneck”в динамике популяции
- 37. Серия слайдов, показывающая расселение Homo sapiens из восточных районов Центральной Африки
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Так какая же стратегия поддержания численности лучше?
- 42. Кривая уязвимости как функция годовой плодовитости и
- 43. кривые дожития кривые выживания lx – кривые
- 44. Тип I. Человек, крупные млекопитающие с заботой
- 45. Кривая типа I – выпуклая – характерна
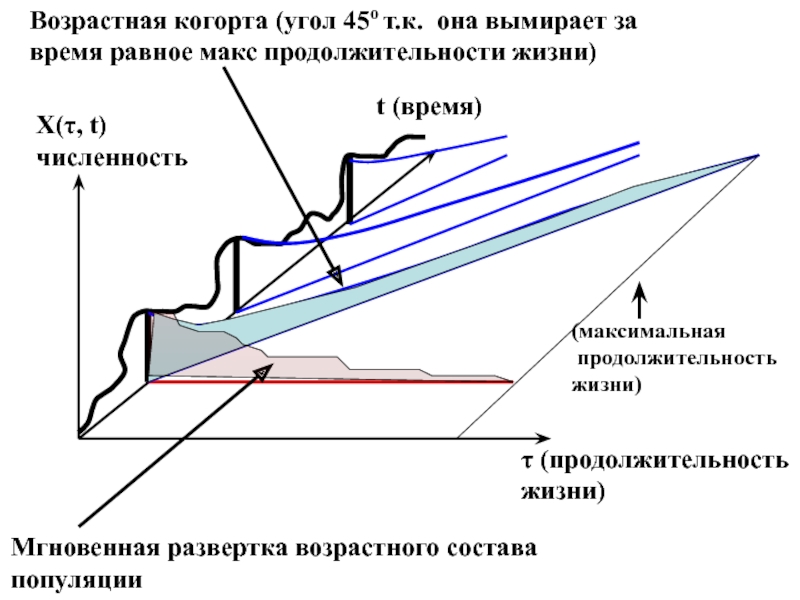
- 46. X(τ, t)численностьτ (продолжительностьжизни)(максимальная продолжительностьжизни)t (время)Мгновенная развертка возрастного
- 47. Выяснилось, что в течении первых 70 суток
- 48. Диагональные lx кривые (смертность, не зависящая от возраста)
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
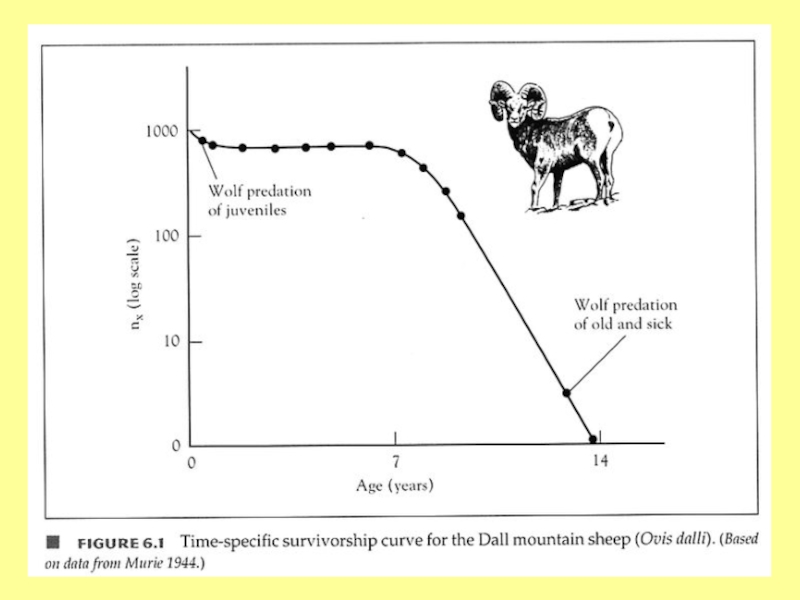
- 53. http://www.alaskanalpinetreks.com/ImageGallery/Wildlife_3/DallSheepRamStandingOnRock.htmlБаран Далла (Ovis dalli)Adolph Murie (1899 – 1974)Из лекций А.М. Гилярова
- 54. Обложка классической работы Адольфа Мури, в которой
- 55. http://scienceblogs.com/tetrapodzoology/2007/06/return_to_the_world_of_sheep.phphttp://www.wildnatureimages.com/Dall'sSheepPictures.htm
- 56. Когортная таблица выживания для барана Далла (Ovis dalli) (построена по материалам анализа 464 черепов)
- 57. x – возраст, точнее, возрастной интервал или
- 58. nx(1000) – то же, что nx, только
- 59. Слайд 59
- 60. Величины, входящие в таблицу выживания (3)ex –
- 61. Графики, которые можно построить на основе таблицы
- 62. ГодыБараныБарано-годыИз лекций А.М. Гилярова (с изменениями)Площадь под
- 63. Графики, которые можно построить на основе таблицы
- 64. Слайд 64
- 65. 60 дниДанные по динамике популяционного роста человеческой вши201000яйцанимфывзрослые3050Тlx mxmxlx 40R0 = 30,9
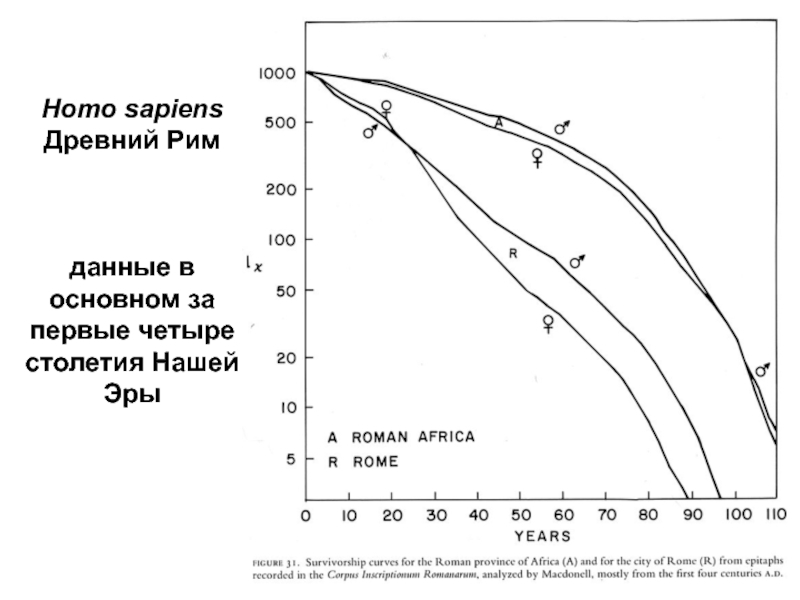
- 66. Homo sapiens Древний Рим данные в основном за первые четыре столетия Нашей Эры
- 67. 100 летВозраст100100040Числовыживших из1000 рожденных(логарифмическая шкала)МужчиныЖенщины
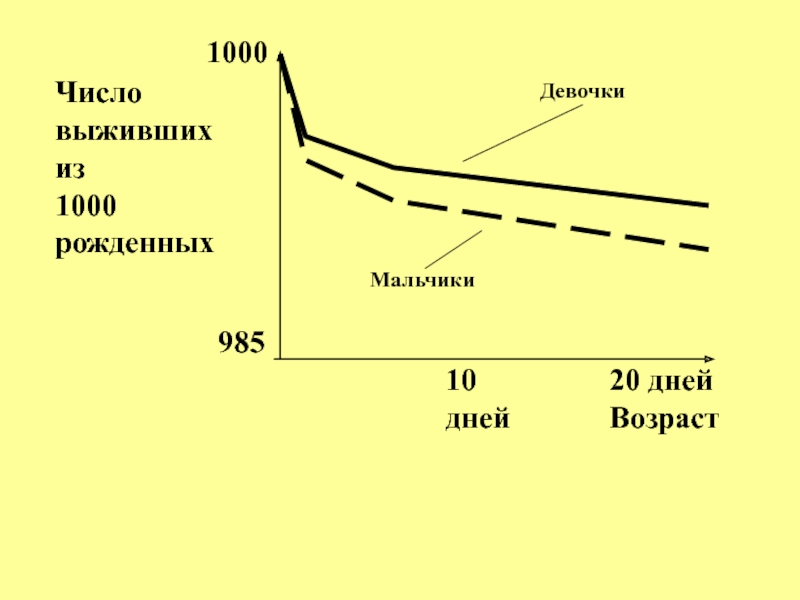
- 68. 20 днейВозраст985100010днейЧисловыживших из1000 рожденныхМальчикиДевочки
- 69. Слайд 69
- 70. X(τ, t)численностьτ (продолжительностьжизни)(максимальная продолжительностьжизни)t (время)Мгновенная развертка возрастного
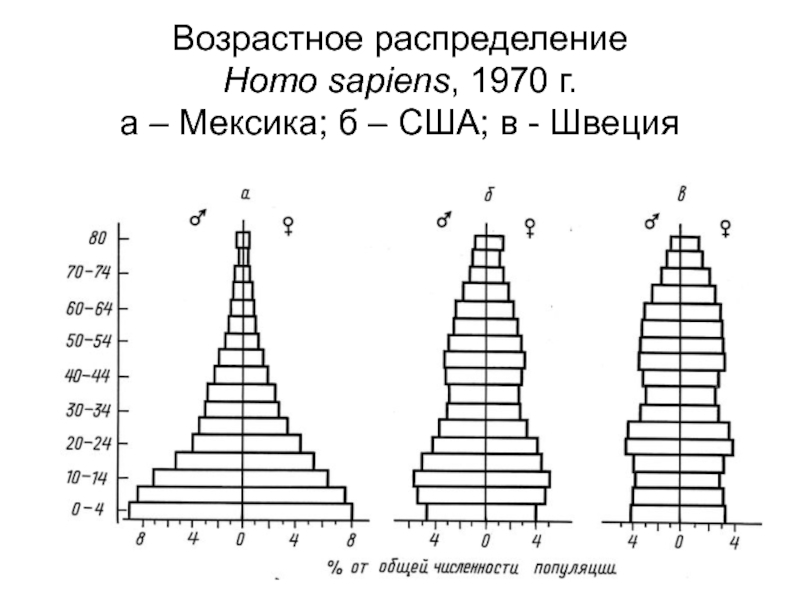
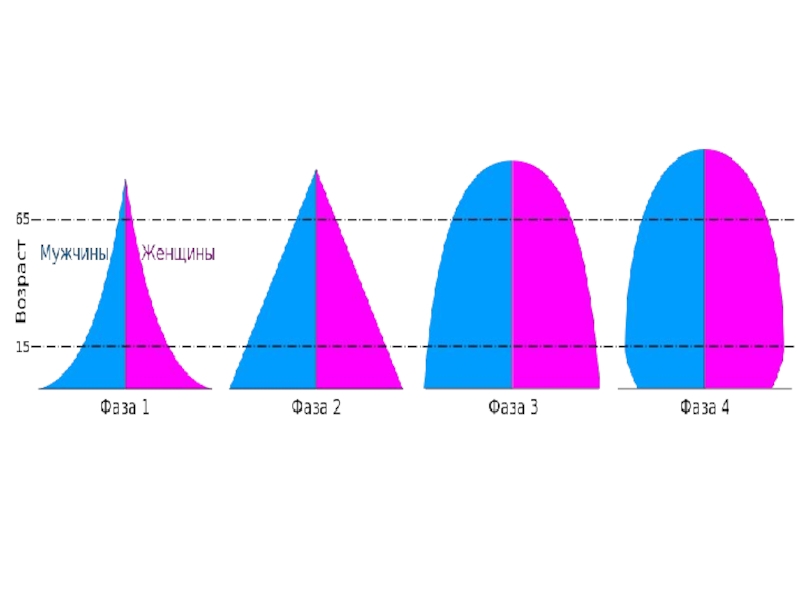
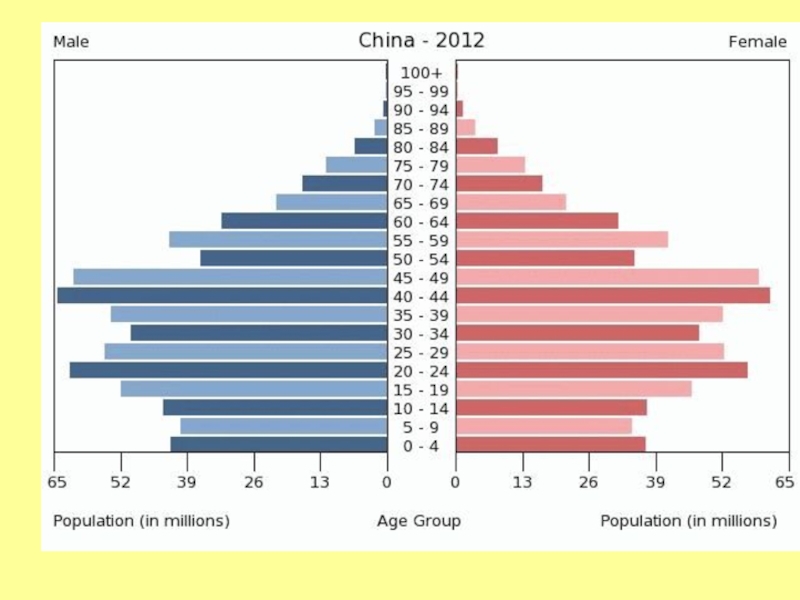
- 71. Возрастное распределение Homo sapiens, 1970 г. а – Мексика; б – США; в - Швеция
- 72. Слайд 72
- 73. Слайд 73
- 74. Слайд 74
- 75. Слайд 75
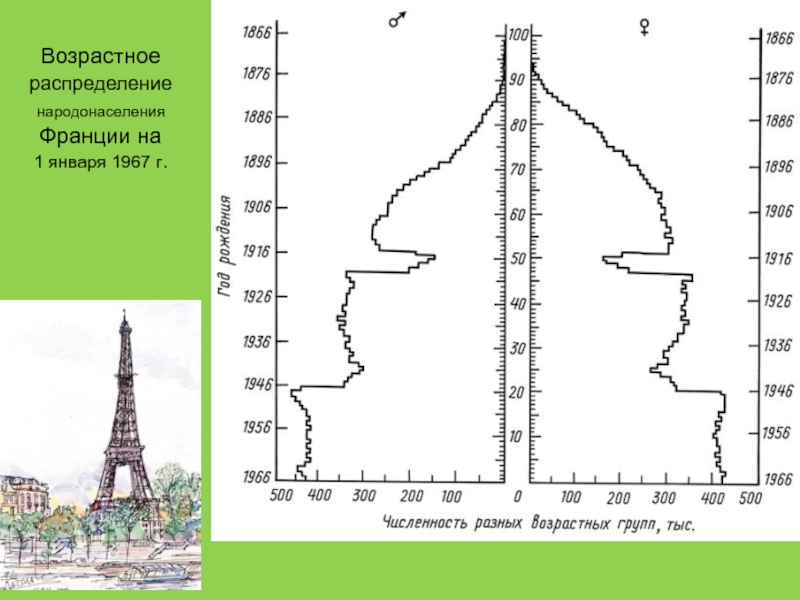
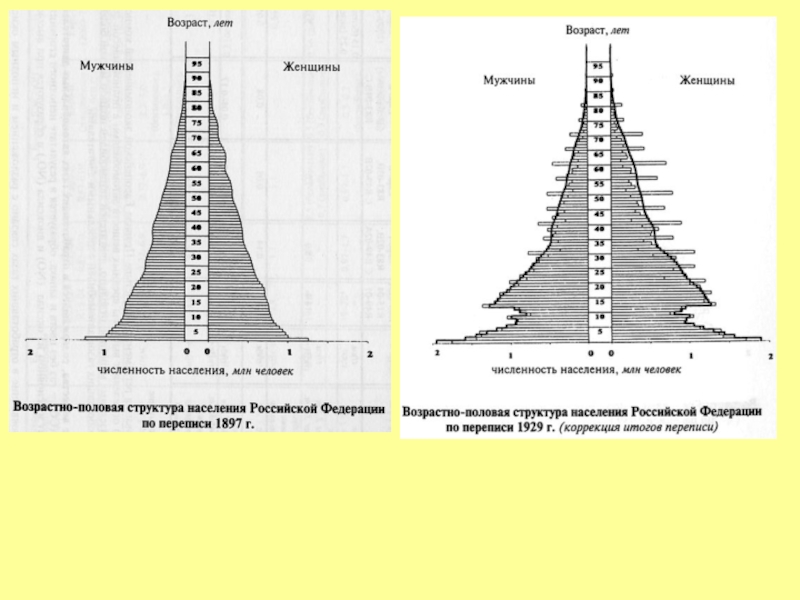
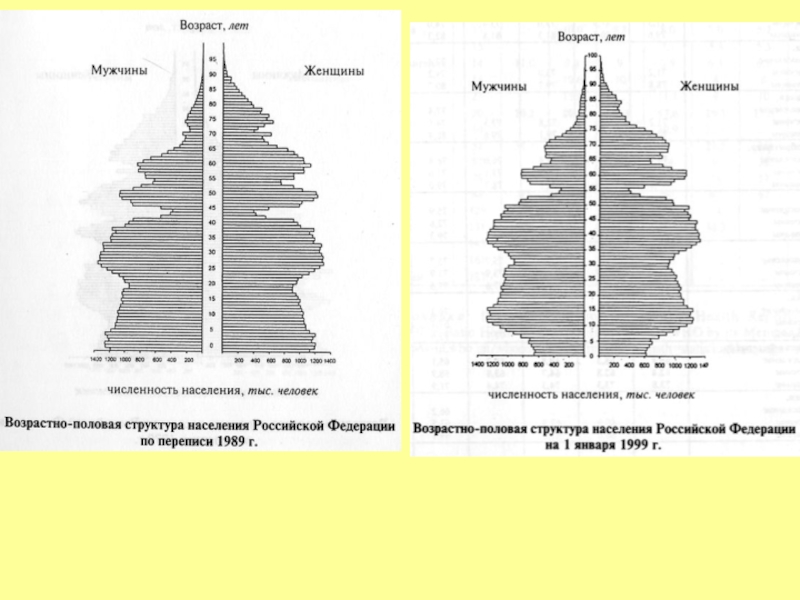
- 76. Возрастное распределение народонаселения Франции на 1 января 1967 г.
- 77. Возрастное распределение народонаселения России на 1 января 1997 г.
- 78. Слайд 78
- 79. Слайд 79
- 80. Слайд 80
- 81. Слайд 81
- 82. Слайд 82
- 83. Слайд 83
- 84. Слайд 84
- 85. Слайд 85
- 86. Слайд 86
- 87. Слайд 87
- 88. Слайд 88
- 89. Слайд 89
- 90. Слайд 90
- 91. Слайд 91
- 92. Слайд 92
- 93. Слайд 93
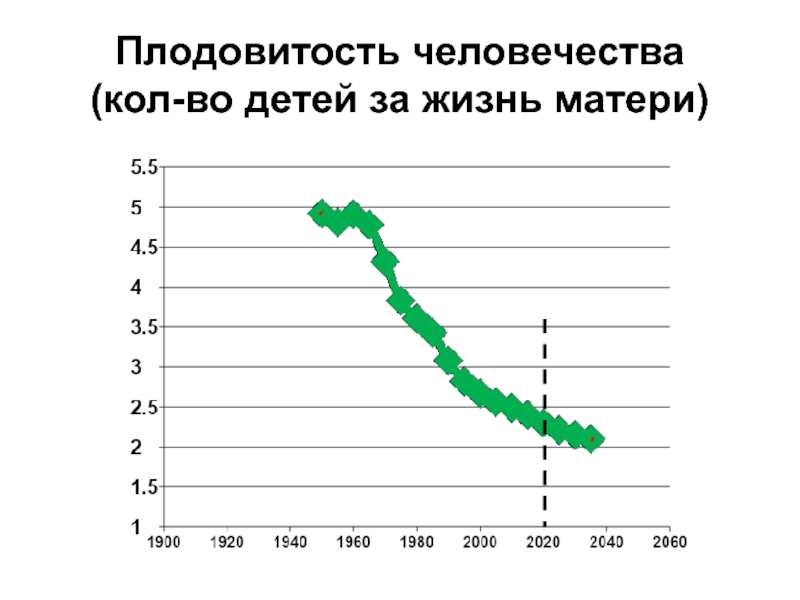
- 94. Плодовитость человечества (кол-во детей за жизнь матери)
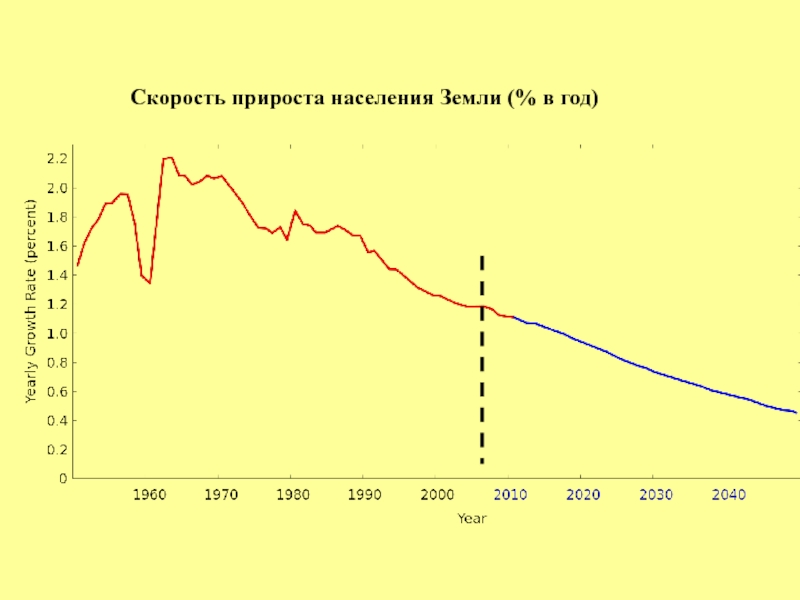
- 95. Скорость прироста населения Земли (% в год)
- 96. Слайд 96
- 97. Скачать презентанцию
Характеристики популяций
Слайды и текст этой презентации
Слайд 9Ещё одно важное обстоятельство, касающееся экспоненциального роста: В популяции, растущей
(или убывающей) экспоненциально, устанавливается стабильное возрастное распределение
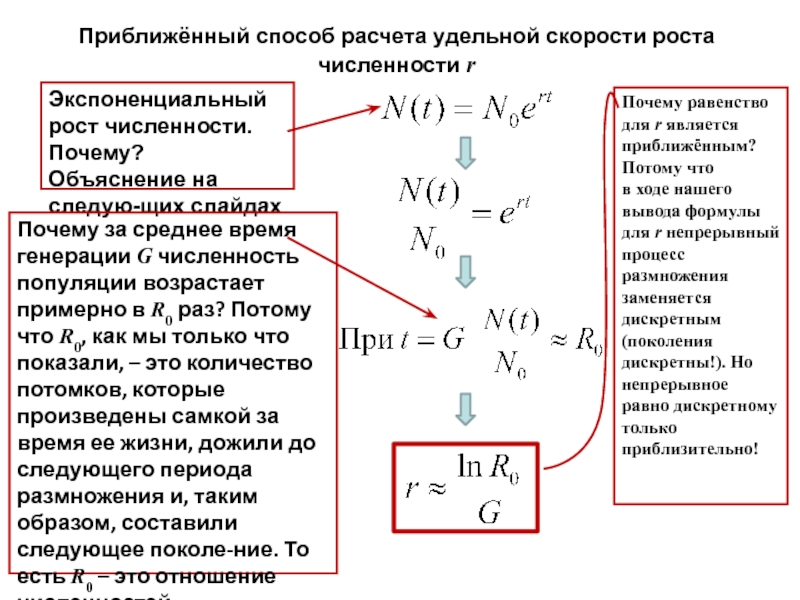
Слайд 12Приближённый способ расчета удельной скорости роста численности r
Экспоненциальный рост
численности. Почему? Объяснение на следую-щих слайдах
Почему за среднее время генерации
G численность популяции возрастает примерно в R0 раз? Потому что R0, как мы только что показали, – это количество потомков, которые произведены самкой за время ее жизни, дожили до следующего периода размножения и, таким образом, составили следующее поколе-ние. То есть R0 – это отношение численностей последовательных поколений, R0 = N(t)/N0Почему равенство для r является приближённым? Потому что
в ходе нашего вывода формулы для r непрерывный процесс размножения заменяется дискретным (поколения дискретны!). Но непрерывное равно дискретному только приблизительно!
Слайд 14Популяция, где по пять детей у молодых матерей (в год
по ребенку с 18 до 22 лет):
R0 = 2.5 G = 20 летПопуляция, где по десять детей у более взрослых матерей (в год по ребенку с 31 до 40 лет):
R0 = 5 G = 35.5 лет
Кому давать орден «Мать-героиня»?
Из лекций А.М. Гилярова
Слайд 15r1 = (ln 2.5) / 20 =
0.916 / 20
= 0.0458 год-1
r2 = (ln 5) / 35.5 =
1.609
/ 35.5 = 0.0453 год-1Кому давать орден «Мать-героиня»?
Из лекций А.М. Гилярова
Замечание 1. А почему все-таки правы те, кто присуждали орден за 10 детей? Потому что r1 может быть реализована только в чреде поколений, то есть если дочери этих матерей будут заводить столько же детей в столь же раннем возрасте (что, конечно, совсем необязательно)
Замечание 2. И величина r1, и величина r2, конечно, завышены, поскольку не учитывают, что la < 1. (Напомним, что R0 = b∙Ta∙la.)
Замечание 3 (точнее, вопрос). Почему r1 > r2 несмотря на то, что R0 у молодых матерей в 2 раза меньше? Ответ «потому что время генерации у них меньше» не годится, потому что время генерации у них меньше только в 1.5 раза.
Слайд 16ОСНОВНЫЕ УРАВНЕНИЯ
(ЛОГИСТИЧЕСКИЙ РОСТ)
Логистический
(S-образный, сигмоидный)
рост замкнутой популяции
(r линейно убывает вслед
за N
пересекая ось в точке N=K)
Для непрерывного размножения:
dN/dt = rN
(1 - N/K) (Ферхюльст – Пирл)Для дискретного:
Nt+1= N tR / (1 + *Ntc)
где К- плотность насыщения,
c – параметр запаздывания,
=(R-1)/K
N t = K/(1+be-rt); b = (K-No)/No
Слайд 18S – образный, близкий к логистическому, рост популяций может наблюдаться
при самых разных механизмах ограничения плотности: 1) нехватки пищи (дафнии, водоросли,
бактерии) 2) накопление продуктов метаболизма (дрожжи) 3) каннибализм (мучные жуки Tribolium) 4) поведенческие механизмы (домовые мыши в эксперименте) … и т.д.
Слайд 21Модель логистического роста
не более, чем одна из множества моделей, описывающих
S-образный рост
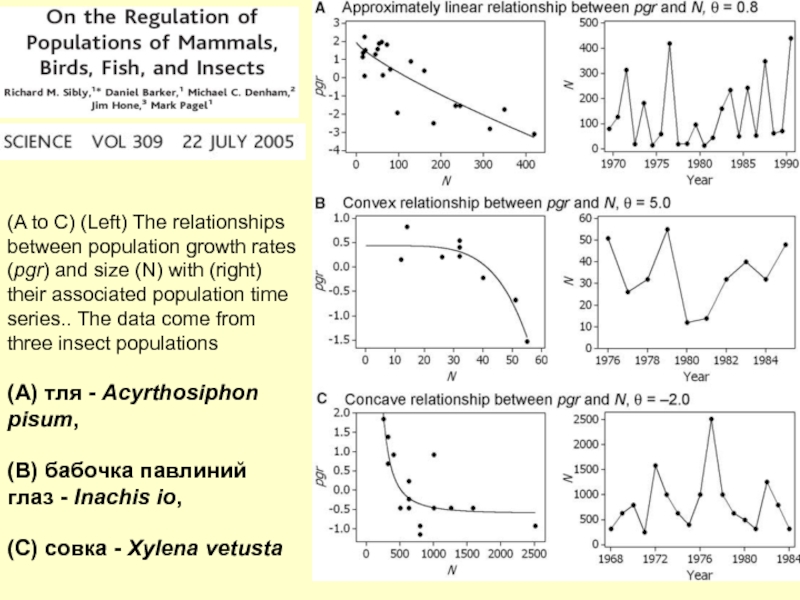
Слайд 22(A to C) (Left) The relationships between population growth rates
(pgr) and size (N) with (right) their associated population time series..
The data come from three insect populations (A) тля - Acyrthosiphon pisum, (B) бабочка павлиний глаз - Inachis io, (C) совка - Xylena vetusta
Слайд 23Где θ – показатель, характеризующий форму зависимости удельной скорости популяционного
роста r0 от плотности
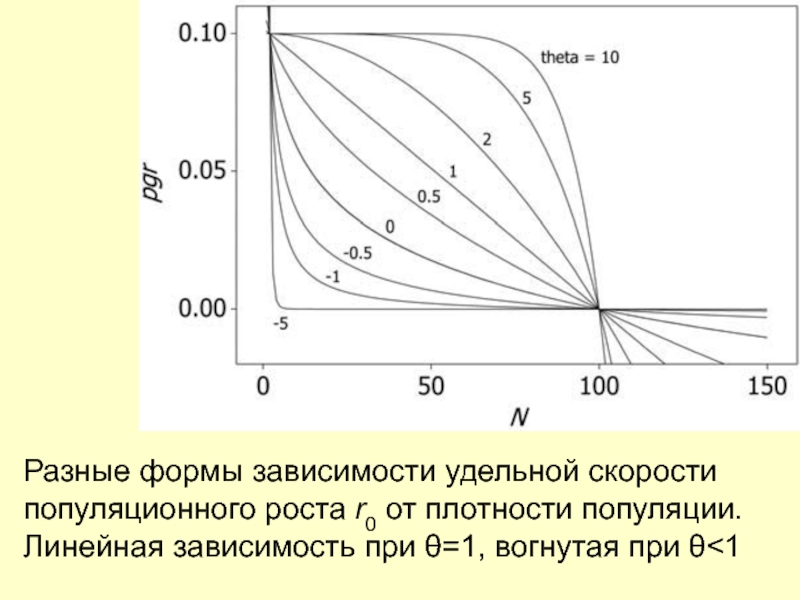
Слайд 24Разные формы зависимости удельной скорости популяционного роста r0 от плотности
популяции. Линейная зависимость при θ=1, вогнутая при θ
Слайд 25Значения показателя тета для четырех таксономических группа из имеющейся базы
данных: (A) млекопитающие, (B) птицы, (C) рыбы, (D) насекомые. Больше +1
– выпуклая, меньше +1 - вогнутая
Слайд 26На 1780 сериях наблюдений (млекопитающие, птицы, рыбы, насекомые), показано, что
скорость популяционного роста высока при низких значениях плотности, но она
очень быстро падает при возрастании плотности. Зависимость описывается вогнутой кривой. Отсюда следует, что большинство популяций в природе существуют при плотностях, близких к ёмкости среды (величина K).
Слайд 27Монотонно
затухающие
Затухающие
Случайные
колебания
Предельные
циклы
время
N
Nt+1= Nt R / (1+a*Ntc)
R
c
Слайд 28СТРАТЕГИИ ПОПУЛЯЦИИ (McArthur, 1967)
r-стратегия
К-стратегия
«отбор на количество»
Основные признаки r-видов:
высокая плодовитость,
короткое время жизни,
обычно малые размеры особей (у
растений мелкие семена), низкая энергия поддержания,
высокие траты энергии на размножение,
Высокая скорость расселения,
низкая конкурентоспособность
«отбор на качество», повышение устойчивости
Основные признаки К-видов:
низкая плодовитость,
значительная продолжительность жизни,
крупные размеры особей и семян, мощные корневые системы,
высокая конкурентоспособность, устойчивость на занимаемой территории,
высокая специализация образа жизни.
забота о потомстве
Слайд 30A trade-off (or tradeoff) is a situation that involves losing one quality or
aspect of something in return for gaining another quality or
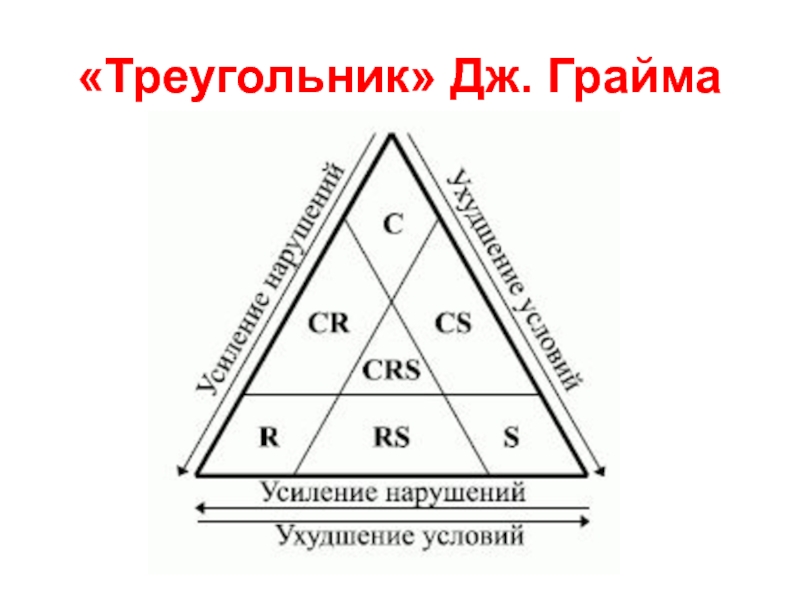
aspect
Слайд 33жизненные стратегии растений (по Л.Г.Раменскому)
Виоленты (силовики) – энергично развиваясь,
они
захватывают территорию и удерживают ее за
собой, подавляя соперников полнотой
использования ресурсов среды аналоги К-стратегии.
Патиенты (выносливцы) – в борьбе за выживание они берут не энергией жизнедеятельности и роста, а своей выносливостью к крайним условиям (ксерофиты – типчак, тенелюб – кислица) - переходная L-стратегия.
Эксплеренты(заполняющие) – имеют очень низкую
конкурентную мощность, но зато они способны очень
быстро захватывать освобождающиеся территории,
выполняя промежутки между сильными растениями,
аналоги R-стратегии
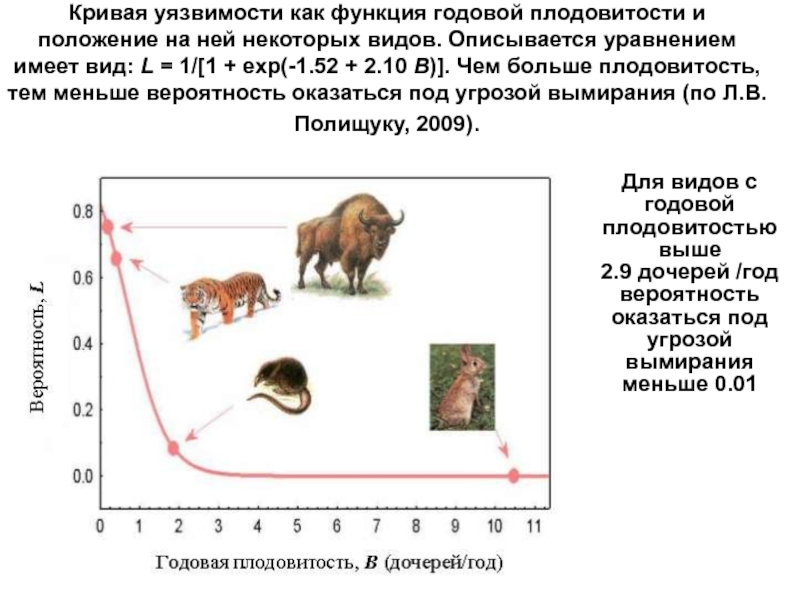
Слайд 42Кривая уязвимости как функция годовой плодовитости и положение на ней
некоторых видов. Описывается уравнением имеет вид: L = 1/[1 +
exp(-1.52 + 2.10 B)]. Чем больше плодовитость, тем меньше вероятность оказаться под угрозой вымирания (по Л.В. Полищуку, 2009).Для видов с годовой плодовитостью выше
2.9 дочерей /год
вероятность оказаться под угрозой вымирания меньше 0.01
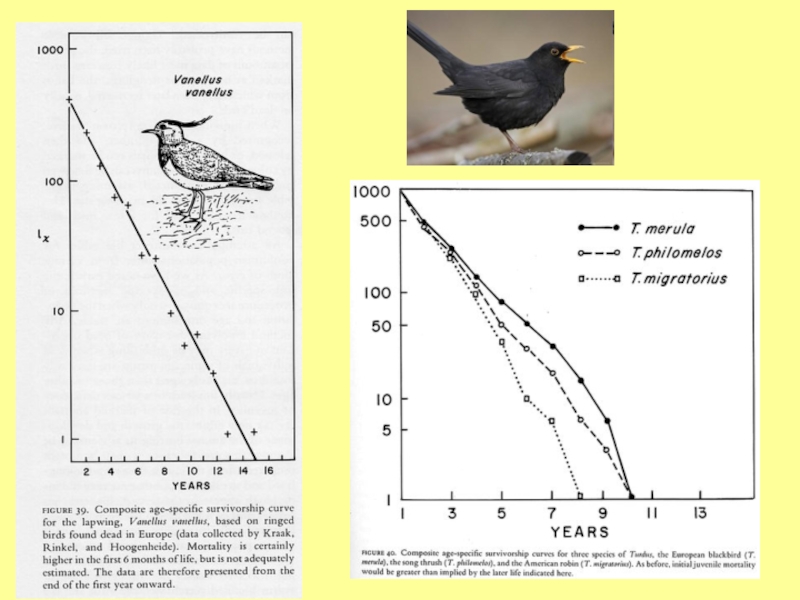
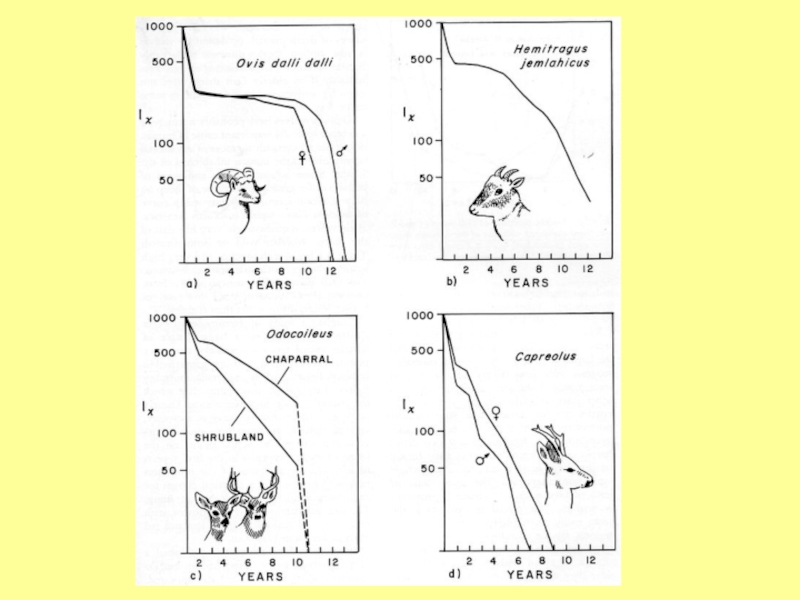
Слайд 44Тип I. Человек, крупные млекопитающие с заботой о потомстве
Тип II.
Некоторые птицы, беспозвоночные (гидра), некоторые растения и рептилии
Тип III. Некоторые
насекомые, водные беспозвоночные, моллюски, рыбы, растенияВозраст
1
10
100
1000
Число выживших логарифмическая шкала
0
ВОЗРАСТНЫЕ КОГОРТЫ
Слайд 45Кривая типа I – выпуклая – характерна для человека и
для большинства млекопитающих. Однако обратите внимание, что для человека и
тем более для млекопитающих, живущих в дикой природе, в отличие от идеального типа I начальный этап кривой выживания характеризуется заметным спадом, соответствующим младенческой смертности.Кривая типа III – вогнутая – характерна для рыб, выметывающих многочисленную икру, морских донных беспозвоночных с планктонной личинкой, паразитов (для паразитов даже говорят о «законе большого числа яиц»).
Кривая типа II – линейная (в полулогарифмическом масштабе!), или диагональная. Ее считают характерной для птиц. Фактически это просто промежуточный случай (между типом I и типом II). Однако он очень важен теоретически, поскольку эта кривая характеризует безвыборочную (неизбирательную, не зависящую от возраста) элиминацию. Кривая этого типа используется во многих экологических моделях. Кроме того, она нередко встречается на практике.
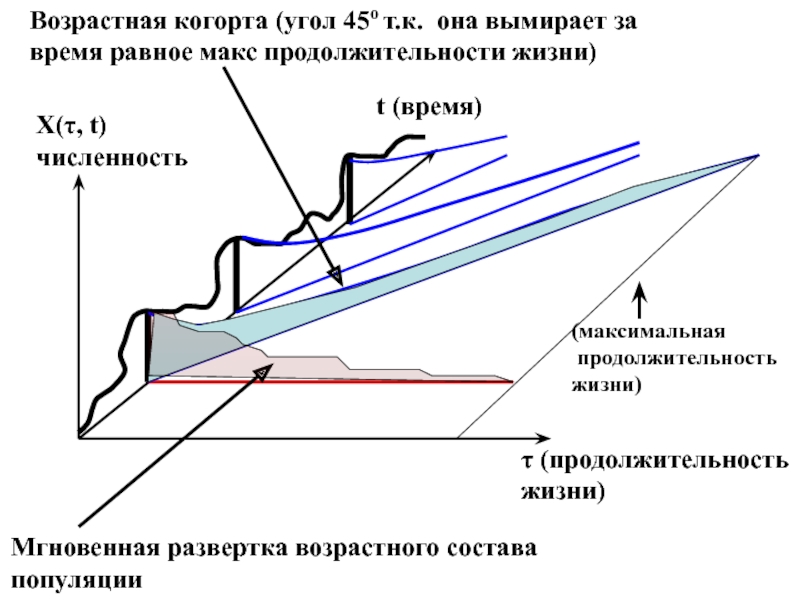
Слайд 46X(τ, t)
численность
τ (продолжительность
жизни)
(максимальная
продолжительность
жизни)
t (время)
Мгновенная развертка возрастного состава популяции
Возрастная когорта
(угол 45о т.к. она вымирает за
время равное макс продолжительности
жизни)
Слайд 47Выяснилось, что в течении первых 70 суток жизни смертность макрели
Scomber scombrus составила 99.9994 % (100% - число отложенных яиц) Из миллиона
икринок получалось 6 личинок, достигших длины 25-39 мм
Слайд 53http://www.alaskanalpinetreks.com/ImageGallery/Wildlife_3/DallSheepRamStandingOnRock.html
Баран Далла (Ovis dalli)
Adolph Murie (1899 – 1974)
Из лекций А.М.
Гилярова
Слайд 54Обложка классической работы Адольфа Мури, в которой он привел данные
по смертности барана Далла в разных возрастах, послужившие основой для
построения кривой выживанияКнига полностью выложена на сайте
(в открытом доступе): http://www.nps.gov/history/history/online_books/fauna5/fauna.htm
В работе Мури в главе 3 приводятся материалы по повозрастной смертности барана Далла (возраст умерших животных определялся по годовым кольцам прироста на поверхности рога; самые ранние кольца находятся на дистальном конце рога). Всего имеются данные по 608 черепам, однако только у 464 из них сохранились рога. У остальных 144 экземпляров возраст мог быть определен лишь приблизительно (по стертости зубов). Эти звери относились к старшим возрастам (≥ 9 лет) и для упрощения расчетов в последующей таблице не учтены.
Слайд 55http://scienceblogs.com/tetrapodzoology/2007/06/return_to_the_world_of_sheep.php
http://www.wildnatureimages.com/Dall'sSheepPictures.htm
Слайд 56Когортная таблица выживания для барана Далла (Ovis dalli) (построена по материалам
анализа 464 черепов)
Слайд 57x – возраст, точнее, возрастной интервал или класс; 0+ означает
интервал от 0 до 1 года (ягнята-сеголетки), 1+ означает интервал
от 1 до 2 лет (годовики) и т.д.mx – число погибших в интервале от 0 до 1 года (x = 0+),
от 1 до 2 лет (x = 1+) и т.д. В случае барана Далла это данные полевых учетов, которые служат основой для всех последующих расчетов
nx – число выживших на начало возрастного интервала x+, или восстановленная численность когорты
Величины, входящие в таблицу выживания
и т.д.
Вы легко можете проверить эти уравнения по таблице выживания на предыдущем слайде!
Слайд 58nx(1000) – то же, что nx, только из расчета на
начальную численность когорты n0 = 1000 особей
lx = nx/n0 –
доля особей, доживших до возраста x; график этой функции есть кривая выживанияdx (в других обозначениях qx) – удельная смертность особей в когорте, или удельная повозрастная смертность
Величины, входящие в таблицу выживания
Слайд 60Величины, входящие в таблицу выживания (3)
ex – средняя («ожидаемая») продолжительность
жизни после достижения возраста x; например, e0 - средняя продолжительность
жизни новорожденных особей. Средняя продолжительность жизни новорожденных особей равна площади под кривой выживанияLx и Tx – вспомогательные величины для определения ex, то есть для расчета площади под кривой выживания
и т.д.
и т.д.
Из лекций Л.В.Полищука
Слайд 61Графики, которые можно построить на основе таблицы выживания
Обратите внимание, что
e0 = 7.1 лет из таблицы выживания численно примерно соответствует
площади под кривой lx (фигуру под кривой можно приблизительно считать прямоугольным треугольником)Возраст, годы
Lx – это площадь указанного прямоугольника. Сумма Lx дает площадь под кривой выживания, то есть T0 = e0.
Кривая выживания (в арифметическом масштабе)
Слайд 62Годы
Бараны
Барано-годы
Из лекций А.М. Гилярова (с изменениями)
Площадь под кривой выживания
Размерность площади
под кривой выживания:
«барано-годы» (в общем случае «особи × возраст»)
Слайд 63Графики, которые можно построить на основе таблицы выживания (на примере
барана Далла)
Удельная смертность особей в когорте (удельная повозрастная смертность)
Хищничество волков
на годовиках?
Хищничество волков на старых и больных
особях
Из лекций Л.В.Полищука
Слайд 64
ПОЛНАЯ ДЕМОГРАФИЧЕСКАЯ ТАБЛИЦА (по Пианка, 1980)
Гипотетическая равновесная популяция с 6
ВК. mx – число потомков одной особи за возрастной период х, lx – доля особей начальной когорты доживших до возраста х, Сумма mx по возрастам х – валовая рождаемость (М),Сумма произведений mx на lx по возрастам х – чистая скорость роста R0, Сумма произведений mx на lx и на возраст х, отнесенное к R0 - среднее время генерации (Т), сумма выживаемостей lx всех возрастов начиная с возраста х, отнесенная к lx- ожидаемая продолжительность жизни возраста ex
СУММЫ: 2.2 (М) 1.00 (R0) 2.78 (Т)
Слайд 6560
дни
Данные по динамике популяционного роста
человеческой вши
20
10
0
0
яйца
нимфы
взрослые
30
50
Т
lx mx
mx
lx
40
R0
= 30,9
Слайд 70X(τ, t)
численность
τ (продолжительность
жизни)
(максимальная
продолжительность
жизни)
t (время)
Мгновенная развертка возрастного состава популяции
Возрастная когорта
(угол 45о т.к. она вымирает за
время равное макс продолжительности
жизни)
