Лекция 5 Механические колебания

Лекция № 5

1. Модель гармонического осциллятора. Свободные незатухающие колебания.
1.1. Основное уравнение движения
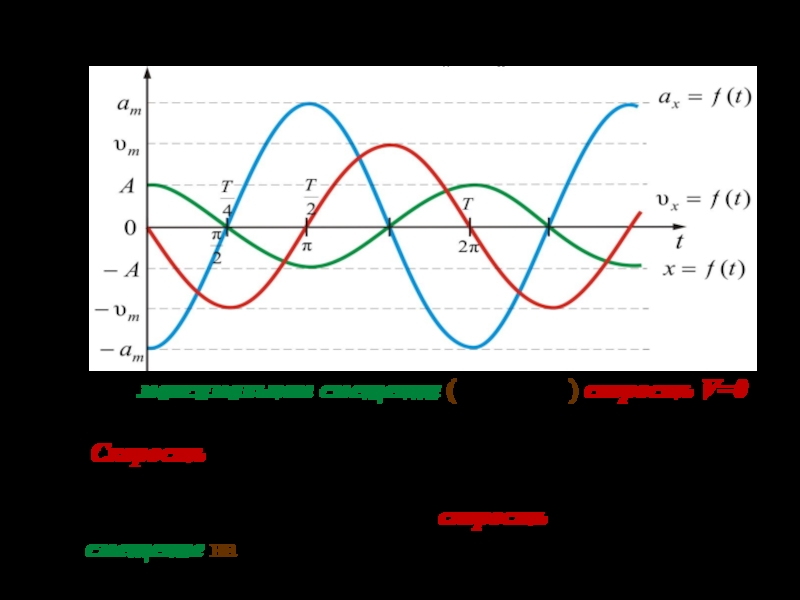
1.2. Основные характеристики.
1.3. Энергия гармонических колебаний.
2. Примеры незатухающих колебаний.
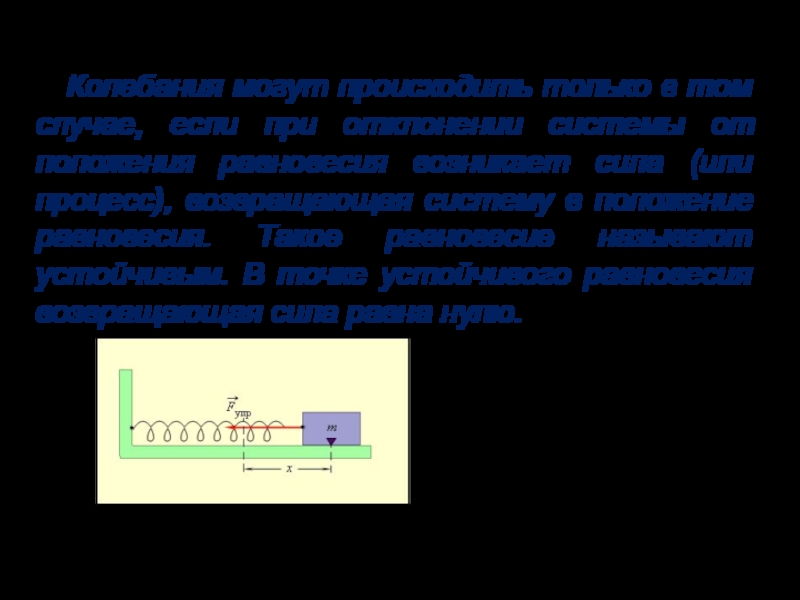
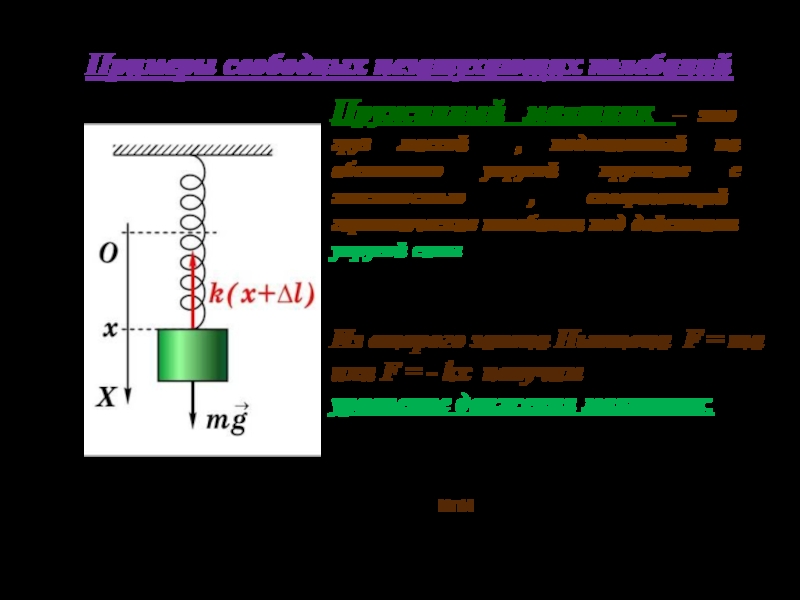
2.1. Пружинный маятник.
2.2. Математический маятник.
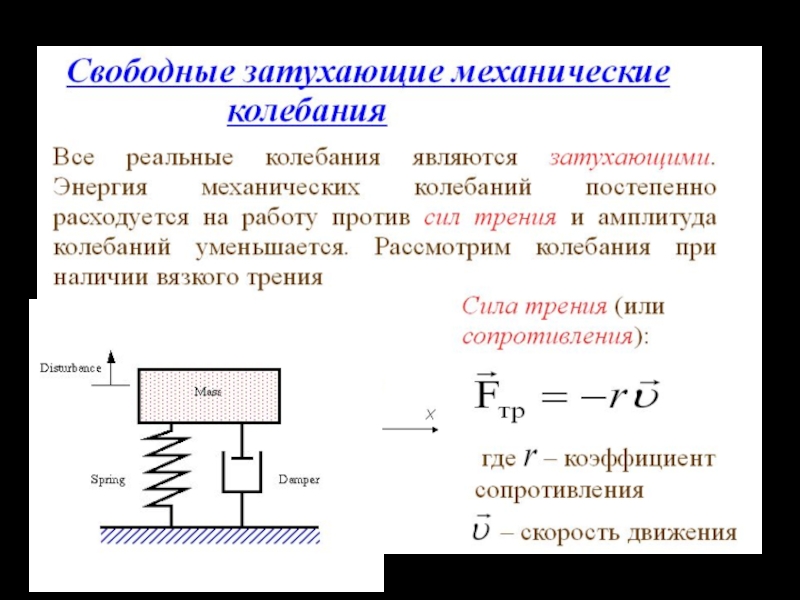
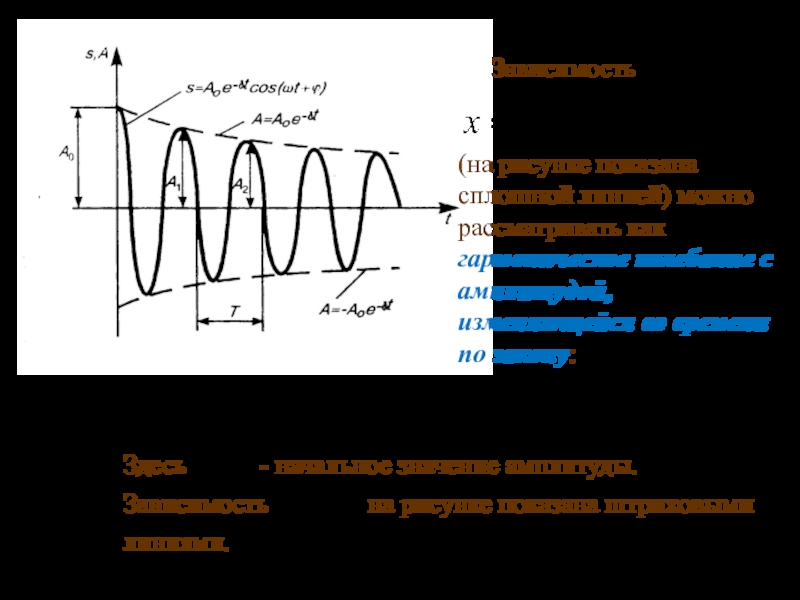
3. Свободные затухающие колебания
3.1. Дифференциальное уравнение
3.2. Основные характеристики колебаний
4. Вынужденные колебания
4.1. Дифференциальное уравнение
4.2. Амплитуда и фаза
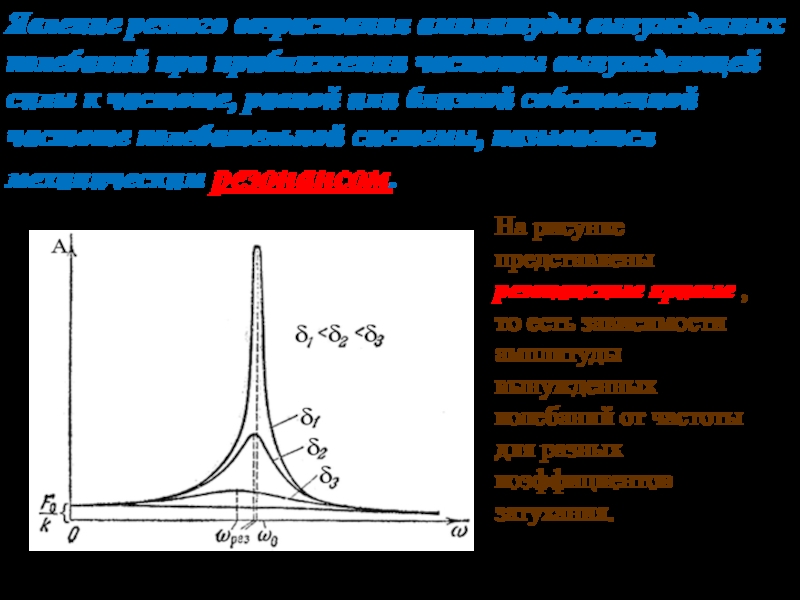
4.3. Резонанс и резонансные кривые.

которого система изменяет свое состояние около точки равновесия.
Колебательные процессы широко

распространены в природе и технике (качели, натянутая струна, переменный электрический ток и т.д.). Физическая природа колебаний может быть разной, поэтому различают колебания механические, электрические, электромагнитные и др. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Поэтому существует единый подход к изучению колебаний различной физической природы.

при отклонении системы от положения равновесия возникает сила (или процесс),

возвращающая систему в положение равновесия. Такое равновесие называют устойчивым. В точке устойчивого равновесия возвращающая сила равна нулю.

Колебания называются свободными (или собственными), если они совершаются за счет

первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменяется со временем по закону косинуса (синуса).

Рассмотрим прямолинейные колебания материаль-ной точки вдоль оси х около положения устойчивого равновесия, принятого за начало координат.

рассмотрим груз массой m, прикрепленный абсолютно упругой пружиной с жесткостью

k к неподвижной стенке и совершающий гармонические колебания под действием упругой силы около точки . Такую зависимость от смещения могут иметь и неупругие силы. Их называют квазиупругими.

Из второго закона Ньютона F = mа и формулы упругой силы F = - kx получим
уравнение движения маятника:



или

Получим основное уравнение динамики

гармонических колебаний, вызываемых упругими силами:

Уравнение, содержащее производные, называют дифференциальным уравнением. Решением дифференциального уравнения всегда является некоторая функция, которая при подстановке ее в уравнение обращает его в тождество.
Можно убедиться, что решением нашего уравнения является функция вида , описывающая колебания гармонического осцилятора

(циклическая) частота,
- фаза колебания в момент времени
- Начальная фаза

колебания в момент времени

Так как косинус изменяется в пределах от +1 до -1, то

может принимать значения от до

Основное характеристики гармонического осциллятора.

представлен на рисунке

время
фаза

промежуток времени Т, называемый периодом колебаний. За один период фаза

колебания получает приращение , то есть

ω0(t + T) = ω0t + 2π

фаза колебания получает приращение т.е

откуда

Величина, обратная периоду колебаний,

число колебаний, совершаемых в единицу
времени, называется частотой колебаний.
Нетрудно видеть, что

Единица частоты - герц (Гц).

по времени является скоростью:
Вторая производная от

Х - ускорение:

Т.е. скорость и ускорение совершают гармонические колебания с той же циклической частотой.
Амплитуды скорости и ускорения соответственно равны
и

Фаза колебаний скорости и ускорения отличается от фазы колеблющейся величины
на и соответственно.

максимальном смещении (

) скорость V=0

Скорость колебаний тела максимальна и равна амплитуде скорости в момент прохождения через положение равновесия ( ), то есть скорость опережает смещение на

равновесия (x = 0) и достигает наибольшего значения, равного амплитуде

ускорения при наибольших смещениях (x = ±A), но по знаку всюду противоположно смещению, то есть смещение и ускорение находятся в противофазе (ускорение опережает смещение на ).

энергии в поле упругой силы
Потенциальная энергия тела U измеряется той

работой, которую произведет возвращающая сила . Так как

, то или

После подстановки выражения для х получаем для потенциальной энергии следующую формулу:

U и K изменяются с частотой

, которая в два раза превышает частоту гармонического колебания.

энергии:
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив

закон сохранения механической энергии, поскольку упругая сила консервативна.

(учтено, что k = mω2)

и наоборот, но их сумма в любой момент времени постоянна.
Из

ранее полученных формул для U и K, а также учитывая, что средние значения
следует:

где Е — полная энергия колебаний

На рисунках представлены графики зависимости х , U и K от времени.

m, подвешенный на абсолютно упругой пружине с жесткостью k, совершающий

гармонические колебания под действием упругой силы

Из второго закона Ньютона F = mа или F = - kx получим
уравнение движения маятника:

или

циклическая частота

период

которую подвешена масса m, сосредоточенная в одной точке (шарик на

длинной тонкой нити).

При отклонении маятника от вертикали, возникает возвращающая сила –


и уравнение движения принимает вид:


где - тангенциальное
ускорение

Уравнение движения маятника:

или

Математический маятник

(

), уравнение движения маятника
можно упростить

Решением этого уравнения будут гармонические колебания вида:




с частотой периодом

период колебаний маятника зависит только от его длины и не зависит от массы груза.

вид :
где kx – возвращающая сила,

– сила трения.

После несложных преобразований имеем:

Введем обозначения:

квадрат собственной частоты незатухающих колебаний

коэффициент затухания

) имеет вид:
Частота

колебаний:

Период:

являются периодическими и в строгом cмыcле к ним неприменимо понятие

периода или частоты. Однако, если затухание мало,
то можно условно
пользоваться понятием
периода как промежутка
времени между
двумя последователь-
ными максимумами
(или минимумами)
колеблющейся
физической величины.

как гармоническое колебание с амплитудой, изменяющейся во времени по закону:

Здесь - начальное значение амплитуды.
Зависимость на рисунке показана штриховыми линиями.

время, за которое амплитуда

уменьшается в е раз. Это условие выражается следующим образом:


Из последнего равенства , то есть

Следовательно, коэффициент затухания – есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.

амплитуд, следующих друг за другом через период Т.
Логарифмический декремент

характеризует, насколько убывает амплитуда колебаний за период

Число колебаний - число колебаний, по истечении которых, амплитуда уменьшается раз.

системы, которая при малых значениях коэффициента затухания равна
Добротность обратна логарифмическому

декременту затухания

Физический смысл добротности выявляется из рассмотрения энергии колебательной системы. Можно показать, что добротность пропорциональна отношению средней энергии , запасенной осциллятором, к средним потерям энергии <-ΔE> за период.

,

круговая частота
обращается в нуль

(колебания прекращаются)
Такой процесс называется апериодическим

тело, возвращающееся в положении равновесия, имеет запас кинетической энергии. В

случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления трения.

осциллятора
Чтобы в реальной колебательной системе

получить
незатухающие колебания, надо компенсировать потери
энергии. Такая компенсация возможна с помощью какого-
либо периодически действующего фактора X(t) ,
изменяющегося по гармоническому закону:

Если рассматривать механические колебания, то роль X(t)
играет внешняя вынуждающая сила

Колебания под действием вынуждающей силы называют вынужденными

на которую кроме упругой силы (– kx) и сил сопротивления

(– rυ) действует добавочная периодическая сила. Уравнение колебательного процесса

где

С учетом обозначений для собственной частоты колебаний
системы и коэффициента затухания приходим к уравнению:

для t >> 1/δ решение представляется в виде
где

- частота вынуждающей силы, а и задаются соответственно формулами:

Следовательно, в установив-шемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими.
Амплитуда B и фаза φ колеба-ний существенно зависят от частоты.

при
некоторой частоте, которую называют резонансной

Чтобы определить резонансную частоту, нужно найти минимум подкоренного выражения в знаменателе. Продифференцировав подкоренное выражение по и приравняв его нулю, получим условие, определяющее .

Значение резонансной амплитуды:

к частоте, равной или близкой собственной частоте колебательной системы, называется

механическим резонансом.

На рисунке представлены резонансные кривые , то есть зависимости амплитуды вынужденных колебаний от частоты для разных коэффициентов затухания.

из положения равновесия под действием постоянной силы той же величины
Добротность

показывает, во сколько раз амплитуда в момент резонанса превышает статическое смещение системы при одинаковой силе.

различных коэффициентов затухания :
1.

2.

3.