Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6. Типовые элементарные звенья (усилительное, интегрирующее, инерционное
Содержание
- 1. Лекция 6. Типовые элементарные звенья (усилительное, интегрирующее, инерционное
- 2. Усилительное (пропорциональное) звено
- 3. Единичная ступенчатая функция 1(t).Рис. 5.1. Типовые воздействия САУ
- 4. Единичная импульсная функция δ(t).Эту функцию можно рассматривать
- 5. Гармоническое воздействие.f(t)=Asin(t+); f(t)=Acos(t+),где - круговая частота; - начальная фаза; А - амплитуда
- 6. Временные характеристики САУРеакция системы (элемента) автоматического управления
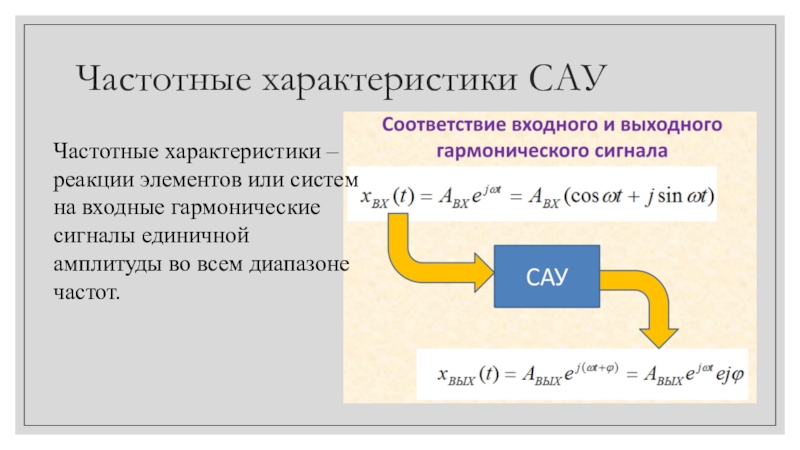
- 7. Частотные характеристики САУЧастотные характеристики – реакции элементов
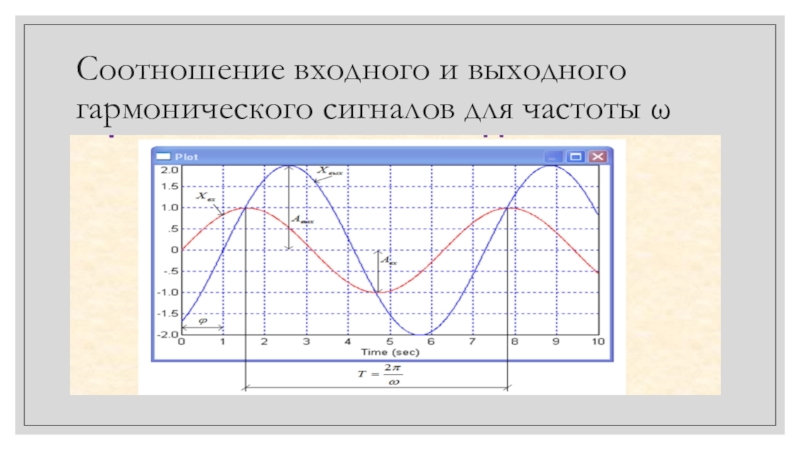
- 8. Соотношение входного и выходного гармонического сигналов для частоты ω
- 9. Частотные характеристики САУ
- 10. Выражения для частотных характеристик
- 11. Частотные характеристикиРис. 5.1. АЧХ и ФЧХ системы
- 12. Логарифмические амплитудно-частотные характеристикиЧастота ωср, на которой L(ω)
- 13. Слайд 13
- 14. Лекция окончена. Вопросы ???
- 15. Скачать презентанцию
Усилительное (пропорциональное) звено
Слайды и текст этой презентации
Слайд 1Лекция 6. Типовые элементарные звенья (усилительное, интегрирующее, инерционное звенья)
Составитель: к.т.н.,
доцент кафедры «Автоматика и телемеханика» Ермилина О.В.
Слайд 4Единичная импульсная функция δ(t).
Эту функцию можно рассматривать как производную от
единичной ступенчатой функции.
Рис. 5.5 – Логарифмические амплитудно-частотные характеристики
Слайд 5Гармоническое воздействие.
f(t)=Asin(t+); f(t)=Acos(t+),
где - круговая частота;
- начальная
фаза;
А - амплитуда
Слайд 6Временные характеристики САУ
Реакция системы (элемента) автоматического управления на единичную ступенчатую
функцию при условии, что система (элемент) до приложения воздействия находилась
в покое, называется переходной функцией h(t).Реакция системы (элемента) автоматического управления на единичную ступенчатую функцию при условии, что система (элемент) до приложения воздействия находилась в покое, называется переходной функцией h(t).
Реакция САУ на единичную импульсную функцию при условии, что система до приложения воздействия находилась в покое, называется весовой функцией w(t).
Слайд 7Частотные характеристики САУ
Частотные характеристики – реакции элементов или систем на
входные гармонические сигналы единичной амплитуды во всем диапазоне частот.
Слайд 12Логарифмические амплитудно-частотные характеристики
Частота ωср, на которой L(ω) пересекается с осью
абсцисс, называется частотой среза. Поскольку lg 1 = 0. то
начало координат чаще всего берется в точке ω = 1 (исключая точку ω = 0, так как lg 0 = -∞). Таким образом, начало координат можно брать в любой точке (в зависимости от интересующего нас диапазона частот, например: ω = 0,05; ω = 0,1; ω = 1; ω = 10 или другие), исключая точку ω = 0. Обычно начало координат помещают в точке ω = 1.Рис. 5.3 – Логарифмические амплитудно-частотные характеристики