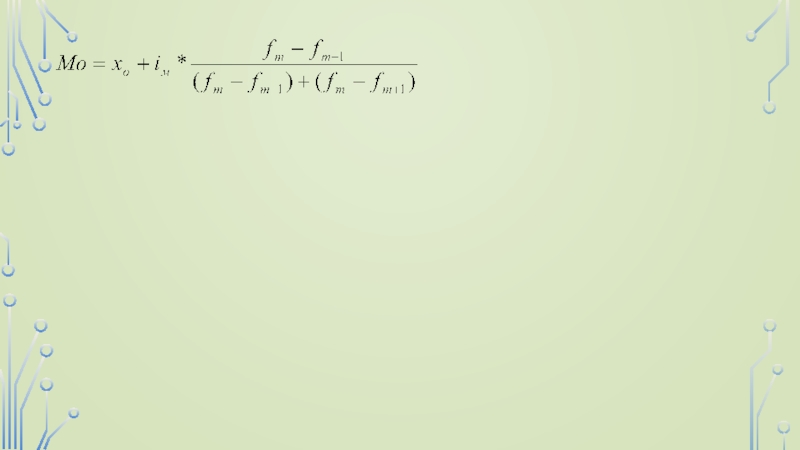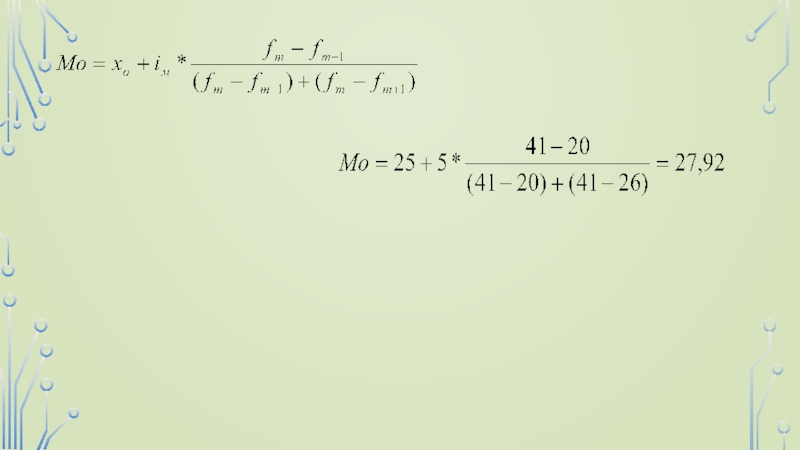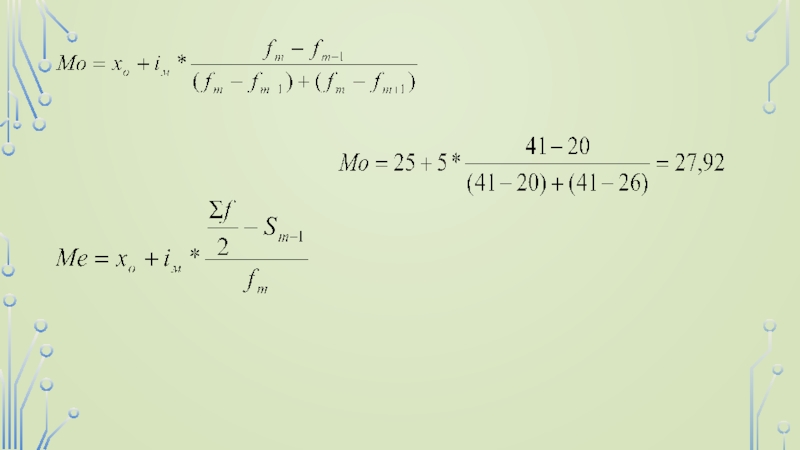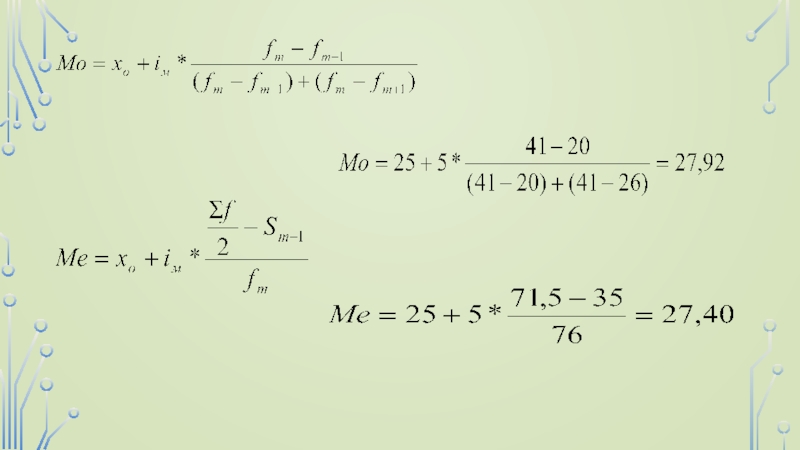Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6. Вариация массовых явлений
Содержание
- 1. Лекция 6. Вариация массовых явлений
- 2. План лекции:1. Понятие вариации и построение вариационного
- 3. 1. Понятие вариации и построение вариационного рядаВариацией
- 4. Причиной вариации являются разные условия существования разных
- 5. Первым этапом статистического изучения вариации являются построение
- 6. Вариационный ряд часто называют рядом распределения. Этот
- 7. Пример ранжированного ряда: Крупные банки города, ранжированные
- 8. Число групп в дискретном вариационном ряду определяется
- 9. Интервальный вариационный ряд представляет собой таблицу, состоящую
- 10. Чаще всего число групп в вариационном ряду
- 11. Если признак принимает небольшое число значений, строится
- 12. ПРИМЕР:Предположим, необходимо построить вариационный ряд распределения предприятий
- 13. Величина интервала составляет:а) при 8 группах б) при
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. 2. Графическое изображение вариационного рядаСущественную помощь в
- 22. Слайд 22
- 23. Диаграмма этого рода часто называется гистограммой
- 24. Великий русский математик А. М. Ляпунов (1857-1918)
- 25. 2.1 Кумулятивное распределениеПреобразованной формой вариационного ряда является
- 26. 2.2 Плотность распределенияЕсли приходится иметь дело с
- 27. Кумулята - «не меньше, чем» . Кумулята или
- 28. Огива - «больше, чем». Обычно огива строится аналогично
- 29. 3. Показатели размера и интенсивности вариации.Медиана распределенияМедиана
- 30. Среднее линейное отклонение (СЛО).Средний модуль, или среднее
- 31. Дисперсия – разброс вокруг средней величины. Безразмерный
- 32. Среднее квадратическое отклонение:СКО показывает, на сколько в
- 33. Скачать презентанцию
План лекции:1. Понятие вариации и построение вариационного ряда2. Графическое изображение вариационного ряда 2.1Кумулятивное распределение 2.2Плотность распределения 3. Показатели размера и интенсивности вариации
Слайды и текст этой презентации
Слайд 2План лекции:
1. Понятие вариации и построение вариационного ряда
2. Графическое изображение
вариационного ряда
Слайд 31. Понятие вариации и построение вариационного ряда
Вариацией значений какого-либо признака
в совокупности называется различие его значений у разных единиц данной
совокупности в один и тот же период или момент времени.В отличие от вариации различия значений признака у одного и того же объекта, у одной и той же единицы совокупности в разные моменты или периоды времени следует называть изменениями во времени и колебаниями. Методы их измерения и изучения отличаются принципиально от методов измерения вариации.
Слайд 4Причиной вариации являются разные условия существования разных единиц совокупности.
Вариация
- необходимое условие существования и развития массовых явлений.
Слайд 5Первым этапом статистического изучения вариации являются построение вариационного ряда -
упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим
(реже) значениям признака и подсчет числа единиц с тем или иным значением признака.Существуют три формы вариационного ряда:
ранжированный ряд,
дискретный ряд,
интервальный ряд.
Слайд 6Вариационный ряд часто называют рядом распределения. Этот термин используется при
изучении вариации как количественных, так и неколичественных признаков. Ряд распределения
представляет собой структурную группировку.Ранжированный ряд — это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
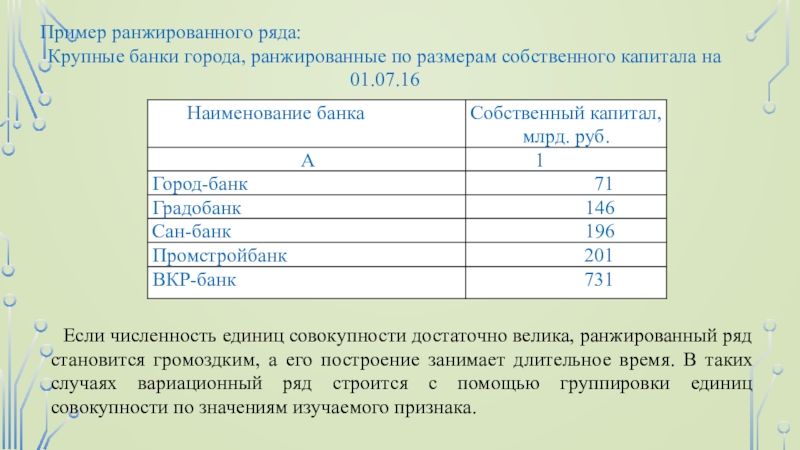
Слайд 7Пример ранжированного ряда:
Крупные банки города, ранжированные по размерам собственного
капитала на 01.07.16
Если численность единиц совокупности достаточно велика, ранжированный ряд
становится громоздким, а его построение занимает длительное время. В таких случаях вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.Слайд 8Число групп в дискретном вариационном ряду определяется числом реально существующих
значений варьирующего признака. Если же признак может принимать хотя и
дискретные значения, но их число очень велико (например, поголовье скота на 1 января года в разных сельхозпредприятиях может составлять от нуля до десятков тысяч голов), тогда строится интервальный вариационный ряд. Интервальный вариационный ряд строится и для изучения признаков, которые могут принимать любые, как целые, так и дробные, значения в области своего существования. Таковы, например, рентабельность реализованной продукции, себестоимость единицы продукции, доход на 1 жителя города, доля лиц с высшим образованием среди населения разных территорий и вообще все вторичные признаки, значения которых рассчитываются путем деления величины одного первичного признака на величину другого.Слайд 9Интервальный вариационный ряд представляет собой таблицу, состоящую из двух граф
(или строк) — интервалов признака, вариация которого изучается, и числа
единиц совокупности, попадающих в данный интервал (частот), или долей этого числа от общей численности совокупности (частостей). При построении интервального вариационного ряда необходимо выбрать оптимальное число групп (интервалов признака) и установить длину интервала. Поскольку при анализе вариационного ряда сравнивают частоты в разных интервалах, необходимо, чтобы величина интервала была постоянной. Оптимальное число групп выбирается так, чтобы в достаточной мере отразилось разнообразие значений признака в совокупности и в то же время закономерность распределения, его форма не искажалась случайными колебаниями частот. Если групп будет слишком мало, не проявится закономерность вариации; если групп будет чрезмерно много, случайные скачки частот исказят форму распределения.Слайд 10Чаще всего число групп в вариационном ряду устанавливают, придерживаясь формулы,
рекомендованной американским статистиком Стерджессом (Sturgess):
m ≈ 1 + 3,322 ×
lg N ; где:где m – количество групп;
N - численность единиц статистической совокупности
Слайд 11Если признак принимает небольшое число значений, строится дискретный вариационный ряд.
Дискретный вариационный ряд - это таблица, состоящая из двух строк
или граф: конкретных значений варьирующего признака хі, и числа единиц совокупности с данным значением признака f -частот (f - начальная буква англ. слова frequency).Слайд 12ПРИМЕР:
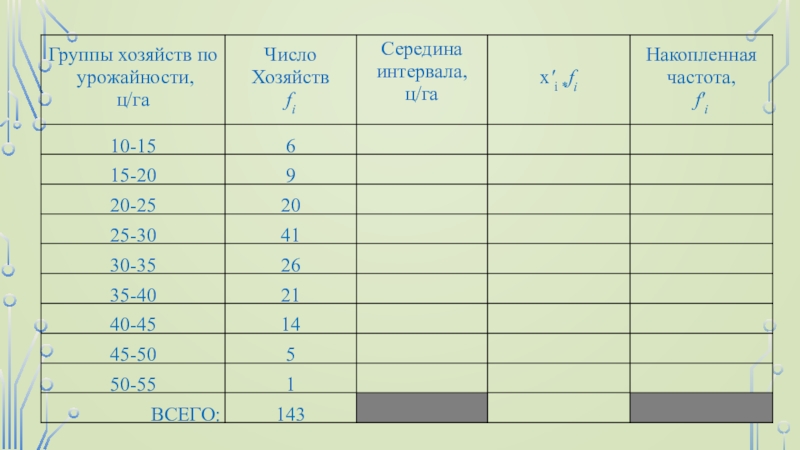
Предположим, необходимо построить вариационный ряд распределения предприятий области по урожайности
зерновых культур за 2016 год. Число сельхозпредприятий, имевших посевы зерновых
культур, составило 143; наименьшее значение урожайности равно 10,7 ц/га, наибольшее - 53,1 ц/га. Имеем по формуле Стерджесса:m≈1+3.322*lg143
m ≈8.16
Рекомендуется построить 8 или 9 групп. Если при 9 группах в интервалах будут пропуски, количество групп уменьшают.
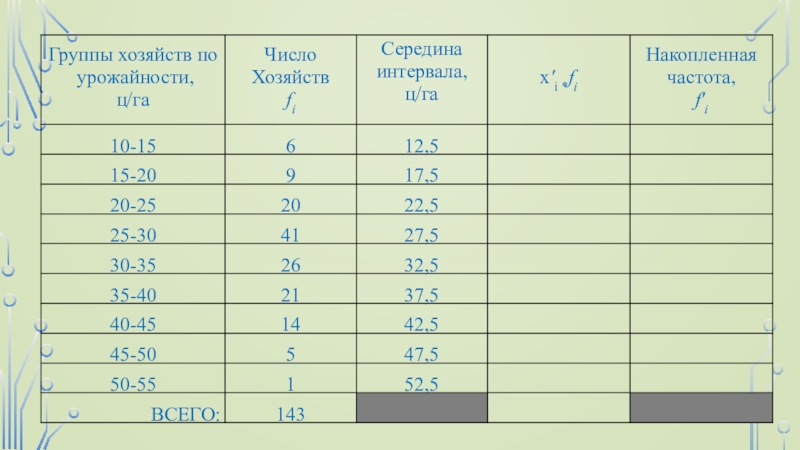
Слайд 13Величина интервала составляет:
а) при 8 группах
б) при 9 группах
Для построения
ряда и анализа вариации значительно лучше иметь по возможности округленные
значения величины интервала и его границ. Поэтому наилучшим решением будет построение вариационного ряда с 9 группами с интервалом, равным 5 ц/ra.Слайд 212. Графическое изображение вариационного ряда
Существенную помощь в анализе вариационного ряда
и его свойств оказывает графическое изображение. Интервальный ряд часто изображается
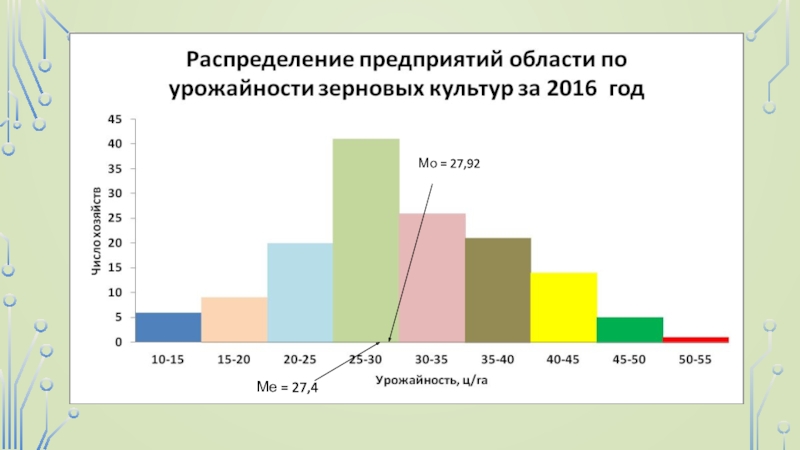
столбиковой диаграммой, в которой основания столбиков, расположенные на оси абсцисс, - это интервалы значений варьирующего признака, а высоты столбиков - частоты, соответствующие масштабу по оси ординат. Графическое изображение распределения хозяйств области по урожайности зерновых культур приведено на рисунке:Слайд 23 Диаграмма этого рода часто называется гистограммой (от греческого слова
«гистос» - ткань, строение).
Данные рисунка показывают характерную для многих признаков
форму распределения: чаще встречаются значения средних интервалов признака, реже - крайние; малые и большие значения признака. Форма этого распределения близка к рассматриваемому в курсе математической статистики закону нормального распределения. Если имеется дискретный вариационный ряд или используются середины интервалов, то графическое изображение такого вариационного ряда называется полигоном (от греч. слова - многоугольник).
Отношение высоты полигона или диаграммы к их основанию рекомендуется в пропорции примерно 5:8.
Слайд 24Великий русский математик А. М. Ляпунов (1857-1918) доказал, что нормальное
распределение образуется, если на варьирующую переменную влияет большое число факторов,
ни один из которых не имеет преобладающего влияния. Случайное сочетание множества примерно равных факторов, влияющих на вариацию урожайности зерновых культур, как природных, так и агротехнических, экономических, создает близкое к нормальному закону распределения распределение хозяйств области по урожайности.Слайд 252.1 Кумулятивное распределение
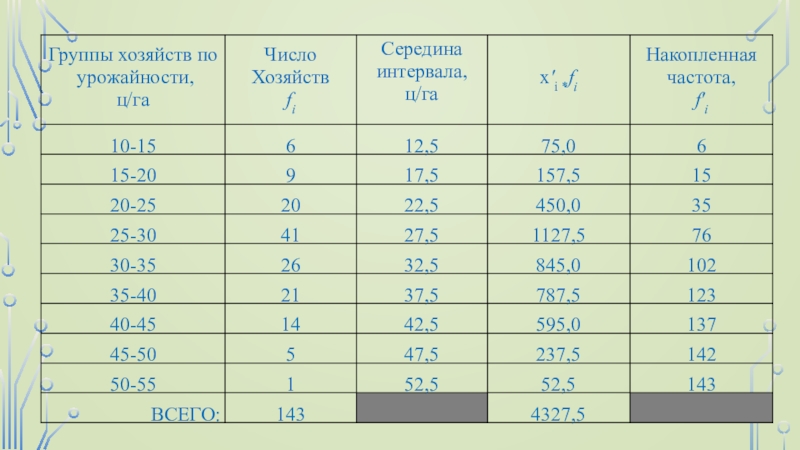
Преобразованной формой вариационного ряда является ряд накопленных частот,
приведенный в таблице в графе 5. Это ряд значений числа
единиц совокупности с меньшими и равными нижней границе соответствующего интервала значениями признака. Такой ряд называется кумулятивным. Можно построить кумулятивное распределение «не меньше, чем», а можно «больше, чем». В первом случае график кумулятивного распределения называется кумулятой, во втором - огивой.Слайд 262.2 Плотность распределения
Если приходится иметь дело с вариационным рядом с
неравными интервалами, то для сопоставимости нужно частоты или частости привести
к единице интервала. Полученное отношение называется плотностью распределения.Где:
fj; - абсолютная плотность распределения в fj-м интервале;
ij - ширина j-го интервала.
Плотность распределения используется как для расчета обобщающих показателей, так и для графического изображения вариационных рядов с неравными интервалами.
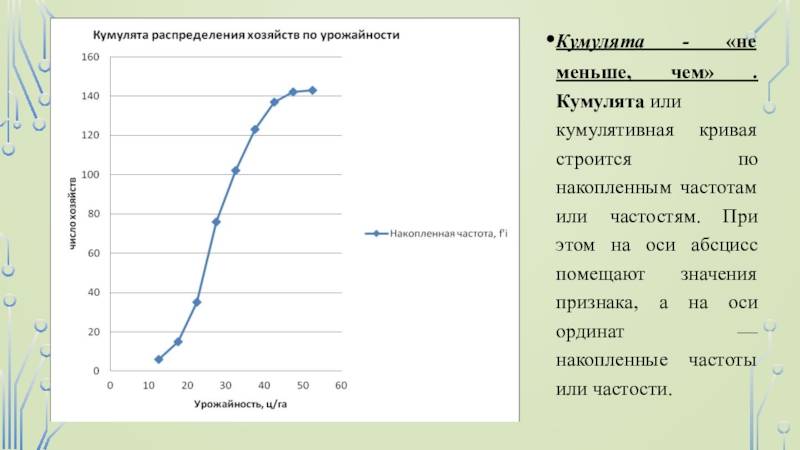
Слайд 27Кумулята - «не меньше, чем» . Кумулята или кумулятивная кривая строится
по накопленным частотам или частостям. При этом на оси абсцисс
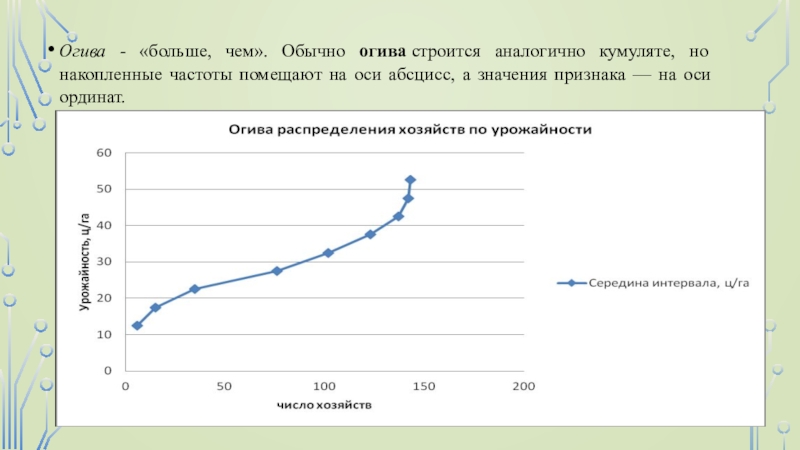
помещают значения признака, а на оси ординат — накопленные частоты или частости.Слайд 28Огива - «больше, чем». Обычно огива строится аналогично кумуляте, но накопленные
частоты помещают на оси абсцисс, а значения признака — на
оси ординат.Слайд 293. Показатели размера и интенсивности вариации.
Медиана распределения
Медиана - величина варьирующего
признака, делящая совокупность на две равные части - со значением
признака меньше медианы и со значениями признака больше медианы.Мода распределения.
В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т.е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается точечной модой.
Слайд 30Среднее линейное отклонение (СЛО).
Средний модуль, или среднее линейное отклонение, по
абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю
середин интервалов от средней арифметической величины, т.е. по формулам:Для несгруппированных данных:
Сгруппированный ряд:
Слайд 31Дисперсия – разброс вокруг средней величины. Безразмерный показатель.
Формула дисперсии:
Простая (для
несгруппированных данных):
Сгруппированный ряд:
или:или
, где
Слайд 32Среднее квадратическое отклонение:
СКО показывает, на сколько в среднем величина показателя
отличается от показателя в каждой группе.
Коэффициент вариации.
Показывает степень однородности
изучаемых явлений.Критерии коэффициента:
V < 33,3% - изучаемая совокупность однородна и средняя типична
V > 33,3% - нетипичность средней.