Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 8
Содержание
- 1. Лекция 8
- 2. Пересечение поверхности с проецирующей плоскостьюЕсли поверхность пересекается
- 3. Пересечение поверхности с плоскостью общего положенияЧтобы построить
- 4. Задача № 9.3
- 5. Решение: Т.к.каркас пирамиды состоит из трех ребер
- 6. Далее определяем пересечение ребер SB и SC
- 7. Соединяем построенные точки между собой с учетом
- 8. Рассмотрим на П2 конкурирующие точкиД и
- 9. Следовательно, на П2 видно, как вершина пирамиды выходит из плоскости.°Д2≡Е2°°Д1Е1
- 10. Рассмотрим на П1 конкурирующие точкиМ и
- 11. Следовательно, на П1 видно, как поверхность пирамиды выходит из плоскости°Д2≡Е2°°Д1Е1°°°М2Н2М1≡Н1
- 12. Пересечение прямой с поверхностьюЗаключаем прямую во вспомогательную
- 13. Пересечение прямой с призматической поверхностьюЗаключаем прямую а
- 14. 3. Находим точки пересечения заданной прямой с
- 15. Задача 9.4 б) стр. 47:
- 16. Заключаем прямую n во вспомогательную фронтально- проецирующую
- 17. Определяем точки пересечения очерковых образующих 1 и
- 18. Образующие 3 и 4 , являются очерком
- 19. Строим фронтальные проекции образующих 3 и 4.
- 20. Т.к. в сечении получается эллипс, четырех точек
- 21. Строим фронтальные проекции образующих 5 и 6
- 22. 4. Определяем видимость прямой. На
- 23. На П2 проекция (·) I2 видима, т.к.
- 24. Простейшее сечение цилиндра –плоскостью, параллельной образующим цилиндра
- 25. Задача 9.4в стр.48: Найти точки пересечения прямой
- 26. Заключаем прямую n во вспомогательную плоскость, проходящую параллельно образующим цилиндра (а‖в) через искомую прямую n.
- 27. 2. Находим горизонтальные следы прямых а и
- 28. Далее находим пересечение следа плоскости Н1 -
- 29. Строим на П2 проекции точек пересечения М2
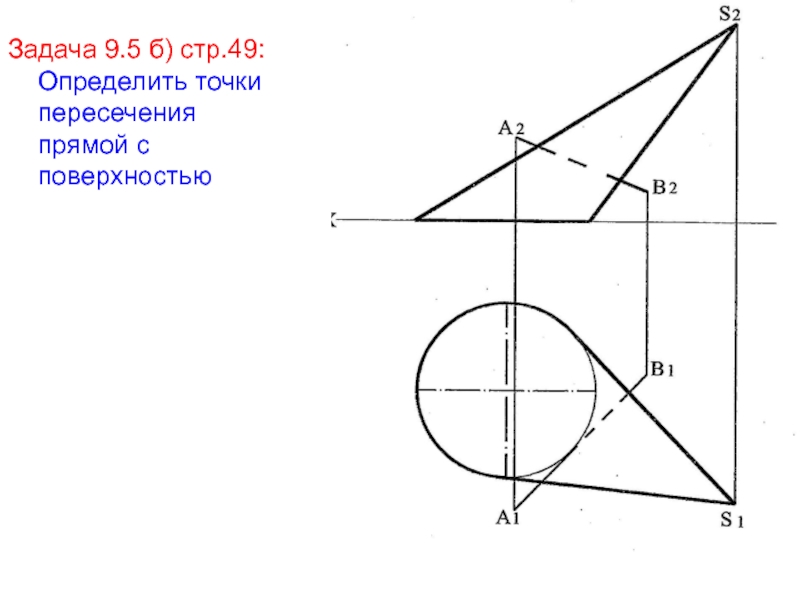
- 30. Задача 9.5 б) стр.49: Определить точки пересечения прямой с поверхностью
- 31. ●SП1●АПростейшее сечение конуса –треугольник, полученный при рассечении
- 32. ●SП1●АПлоскость зададим пересекающимися прямыми: (АВ) и (m), проходящей через вершину конуса « S ».●Вm
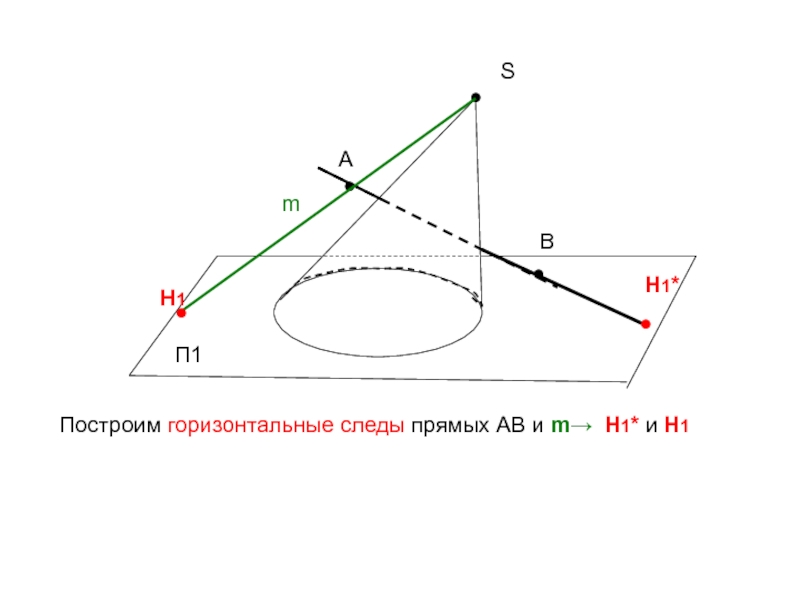
- 33. ●SП1●АПостроим горизонтальные следы прямых АВ и m→ Н1* и Н1●Вm●●Н1Н1*
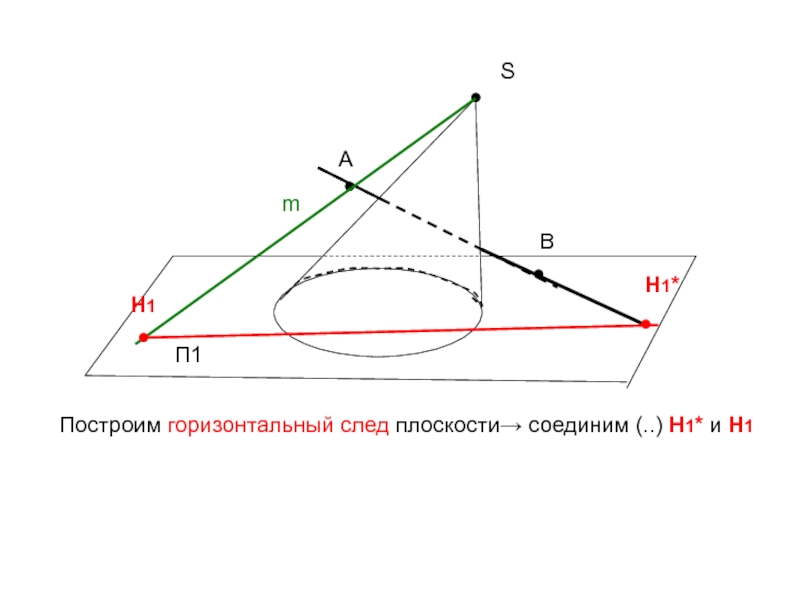
- 34. ●SП1●АПостроим горизонтальный след плоскости→ соединим (..) Н1* и Н1●Вm●●Н1Н1*
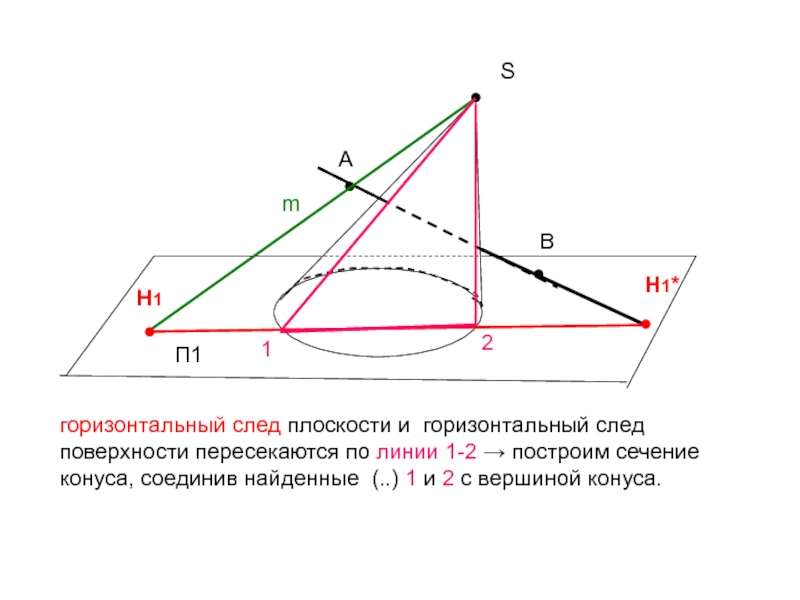
- 35. ●SП1●Агоризонтальный след плоскости и горизонтальный след поверхности
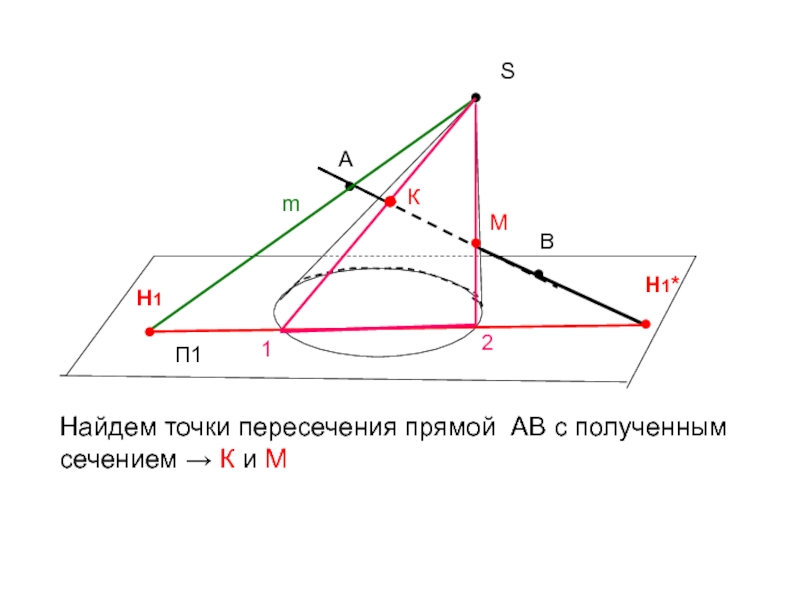
- 36. ●SП1●АНайдем точки пересечения прямой АВ с полученным сечением → К и М●Вm●Н1Н1*12●●●КМ
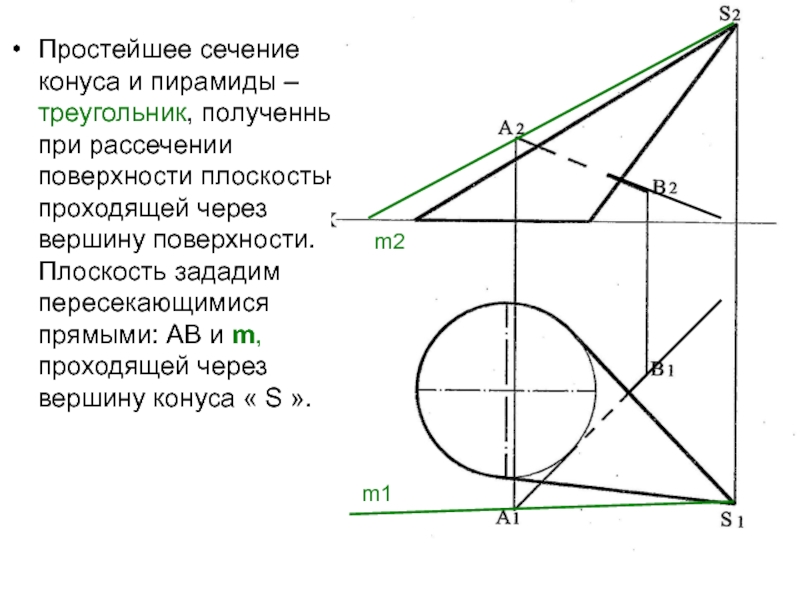
- 37. Простейшее сечение конуса и пирамиды –треугольник, полученный
- 38. Строим горизонтальный след плоскости ( Н1-Н*1 ).По
- 39. Находим точки пересечения заданной прямой с полученным
- 40. Определяем видимость прямой. На П1 проекция точки
- 41. Задача 9.5 а) стр.49: Определить точку пересечения
- 42. Задачу решаем методом замены плоскостей проекций.Главный элемент-
- 43. Строим проекцию сферы на П4.Заключаем прямую во
- 44. Строим точки пересечения заданнойпрямой с полученным сечением
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 8
Пересечение поверхности с проецирующей плоскостью.
Пересечение поверхности с плоскостью общего
положения.
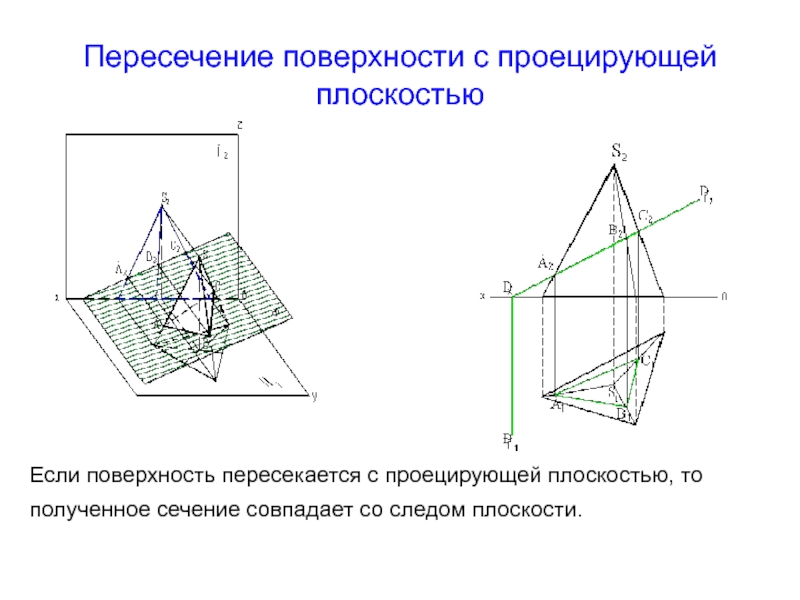
Слайд 2Пересечение поверхности с проецирующей плоскостью
Если поверхность пересекается с проецирующей плоскостью,
то полученное сечение совпадает со следом плоскости.
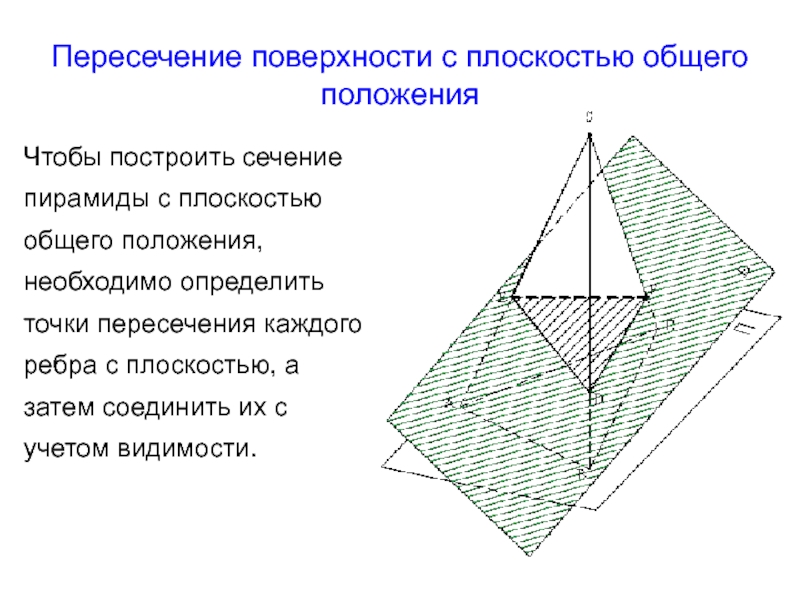
Слайд 3Пересечение поверхности с плоскостью общего положения
Чтобы построить сечение пирамиды с
плоскостью общего положения, необходимо определить точки пересечения каждого ребра с
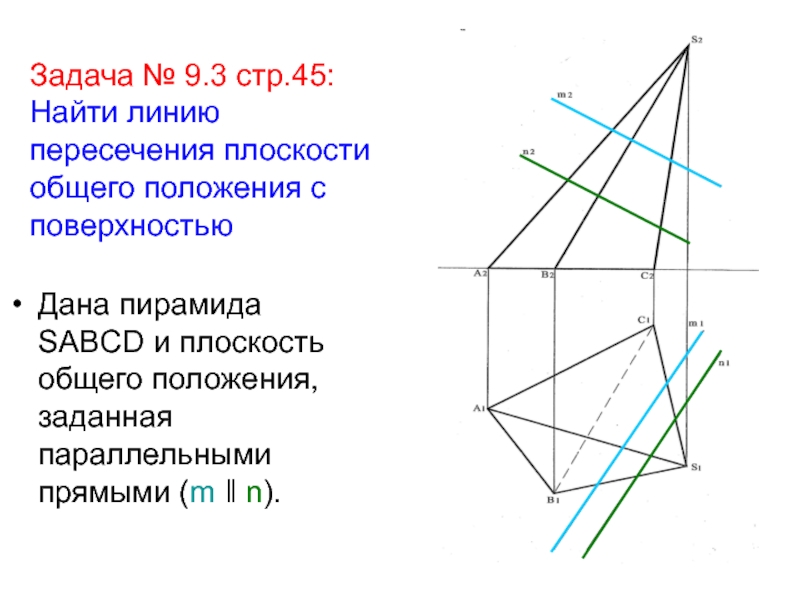
плоскостью, а затем соединить их с учетом видимости.Слайд 4 Задача № 9.3 стр.45: Найти линию пересечения плоскости общего положения
с поверхностью
Дана пирамида SABCD и плоскость общего положения, заданная параллельными
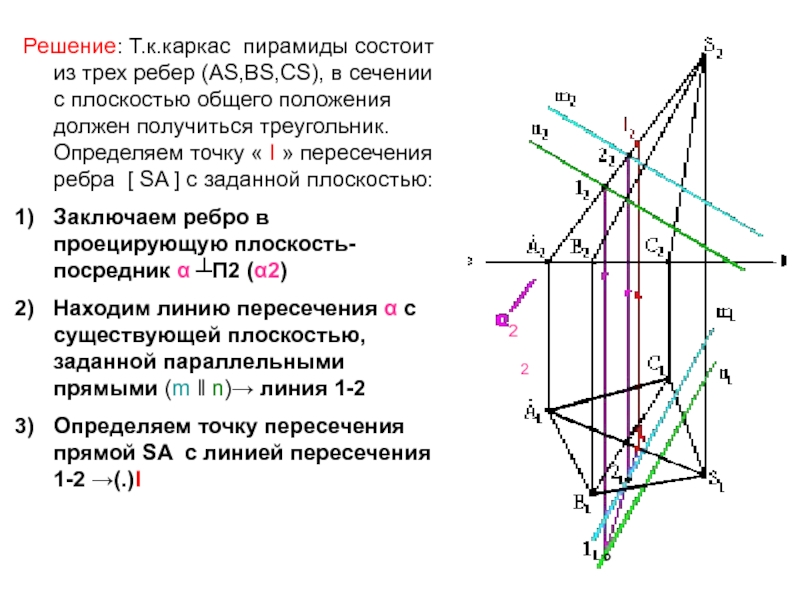
прямыми (m ‖ n).Слайд 5Решение: Т.к.каркас пирамиды состоит из трех ребер (АS,ВS,СS), в сечении
с плоскостью общего положения должен получиться треугольник. Определяем точку «
I » пересечения ребра [ SA ] с заданной плоскостью:Заключаем ребро в проецирующую плоскость- посредник α ┴П2 (α2)
Находим линию пересечения α с существующей плоскостью, заданной параллельными прямыми (m ‖ n)→ линия 1-2
Определяем точку пересечения прямой SA с линией пересечения 1-2 →(.)I
2
2
°
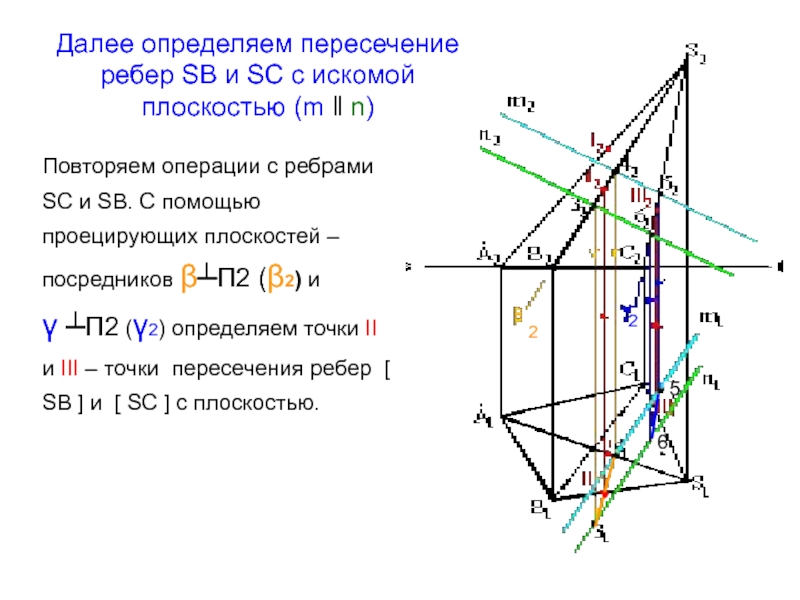
Слайд 6Далее определяем пересечение ребер SB и SC с искомой плоскостью
(m ‖ n)
Повторяем операции с ребрами SС и SB. С
помощью проецирующих плоскостей –посредников β┴П2 (β2) и γ ┴П2 (γ2) определяем точки II и III – точки пересечения ребер [ SB ] и [ SC ] с плоскостью.2
2
●
6
5
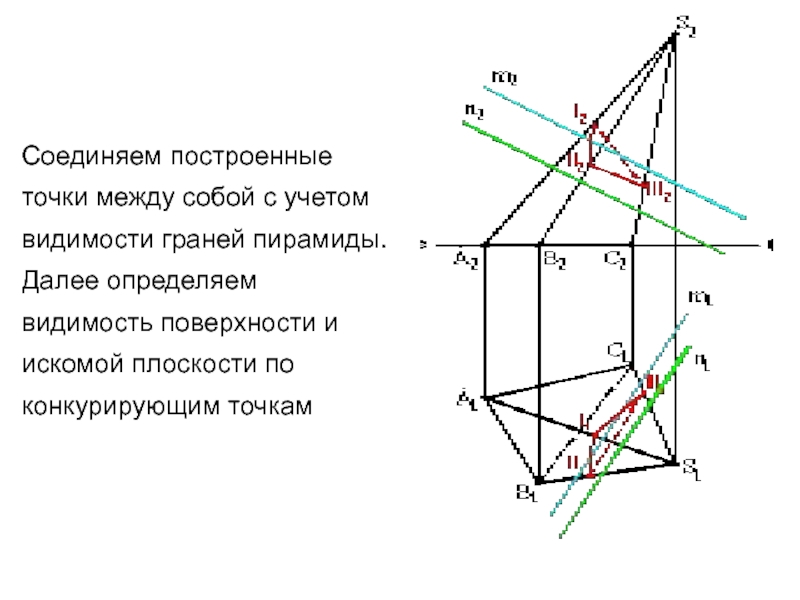
Слайд 7Соединяем построенные точки между собой с учетом видимости граней пирамиды.
Далее определяем видимость поверхности и искомой плоскости по конкурирующим точкам
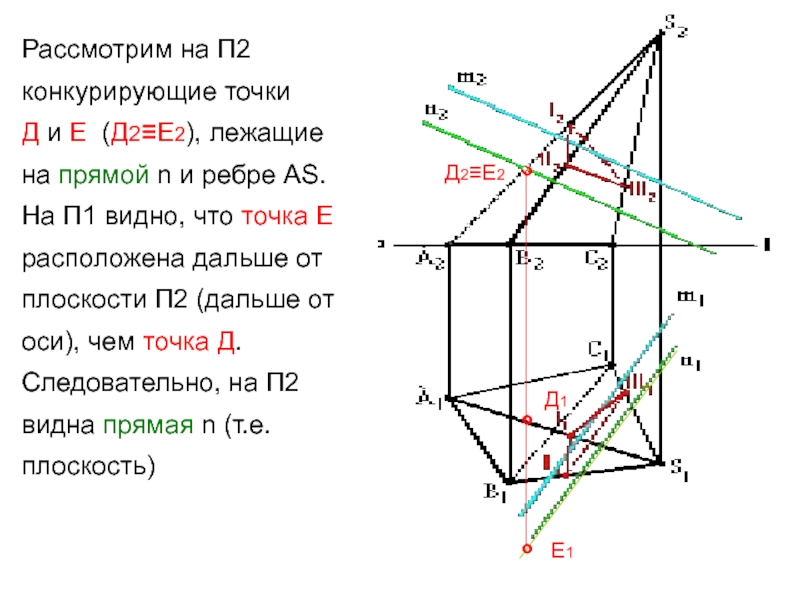
Слайд 8Рассмотрим на П2 конкурирующие точки
Д и Е (Д2≡Е2), лежащие
на прямой n и ребре АS. На П1 видно, что
точка Е расположена дальше от плоскости П2 (дальше от оси), чем точка Д. Следовательно, на П2 видна прямая n (т.е. плоскость)°
Д2≡Е2
°
°
Д1
Е1
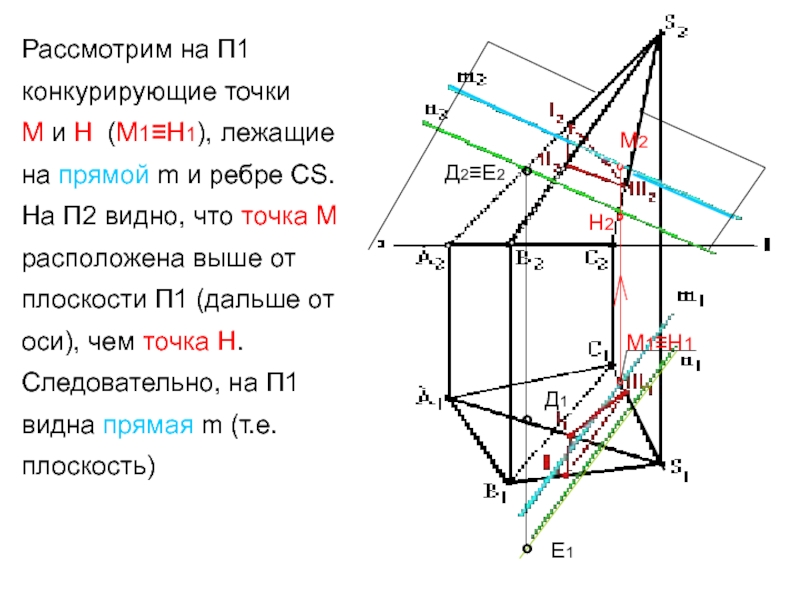
Слайд 10Рассмотрим на П1 конкурирующие точки
М и Н (М1≡Н1), лежащие
на прямой m и ребре CS. На П2 видно, что
точка М расположена выше от плоскости П1 (дальше от оси), чем точка Н. Следовательно, на П1 видна прямая m (т.е. плоскость)°
Д2≡Е2
°
°
Д1
Е1
°
°
°
М2
Н2
М1≡Н1
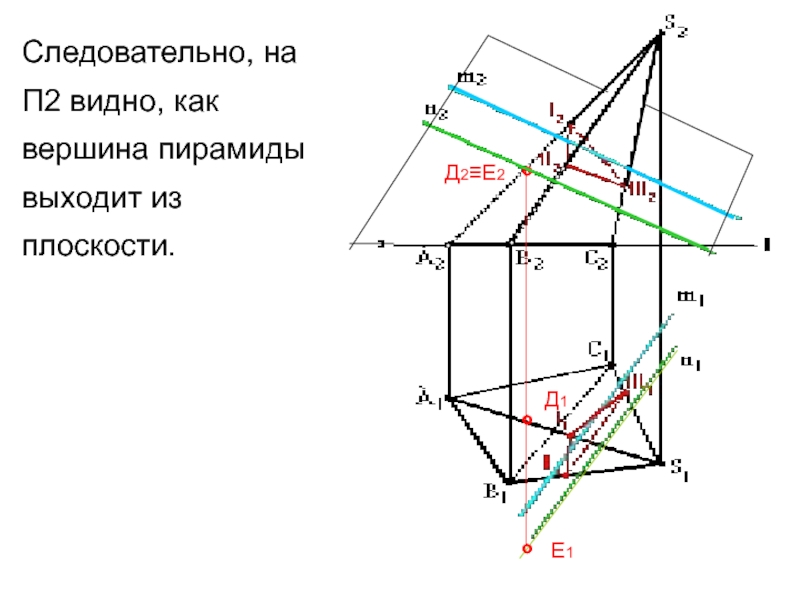
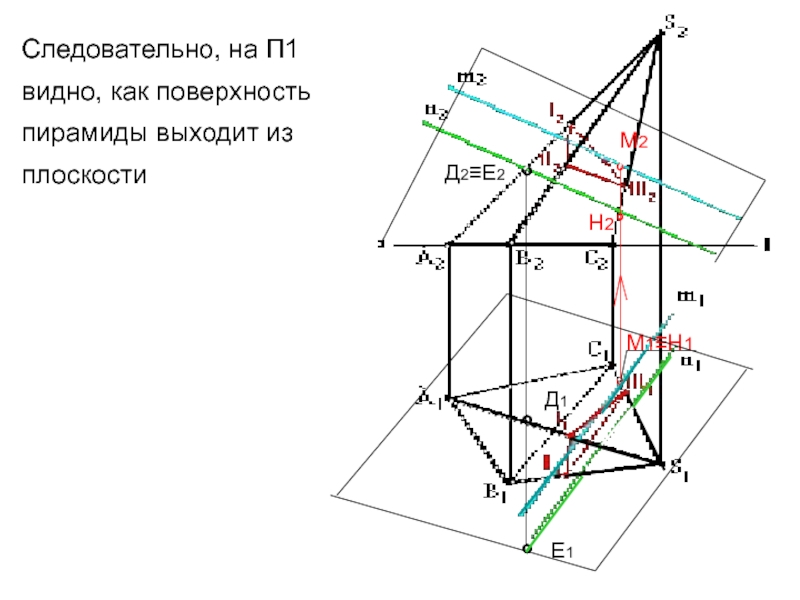
Слайд 11Следовательно, на П1 видно, как поверхность пирамиды выходит из плоскости
°
Д2≡Е2
°
°
Д1
Е1
°
°
°
М2
Н2
М1≡Н1
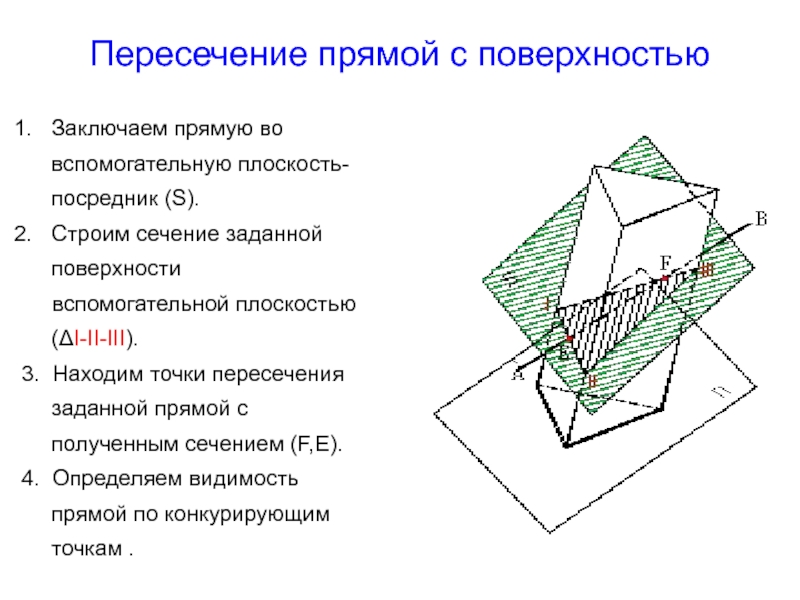
Слайд 12Пересечение прямой с поверхностью
Заключаем прямую во вспомогательную плоскость-посредник (S).
Строим сечение
заданной поверхности
вспомогательной плоскостью (ΔI-II-III).
3. Находим точки пересечения
заданной прямой с полученным сечением (F,E).4. Определяем видимость прямой по конкурирующим точкам .
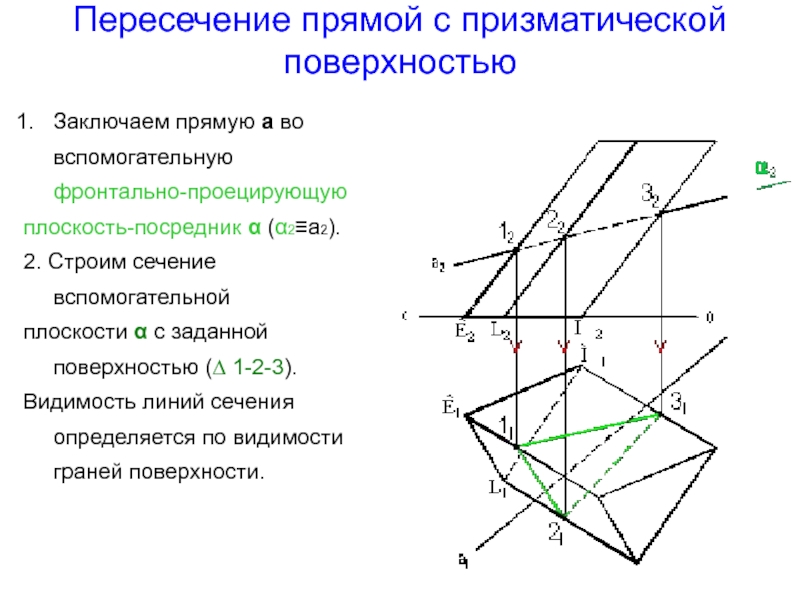
Слайд 13Пересечение прямой с призматической поверхностью
Заключаем прямую а во вспомогательную фронтально-проецирующую
плоскость-посредник α (α2≡а2).
2. Строим сечение вспомогательной
плоскости α с заданной
поверхностью (∆ 1-2-3).Видимость линий сечения определяется по видимости граней поверхности.
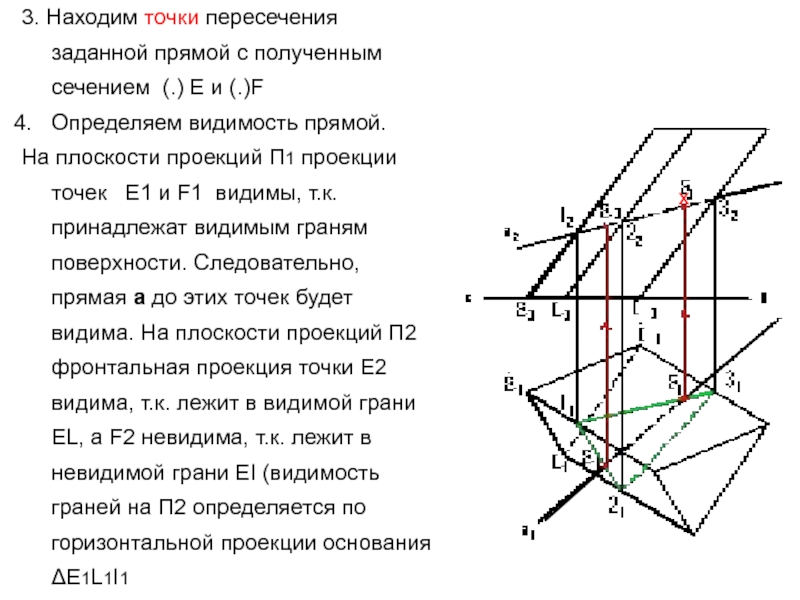
Слайд 143. Находим точки пересечения заданной прямой с полученным сечением (.)
E и (.)F
Определяем видимость прямой.
На плоскости проекций П1
проекции точек Е1 и F1 видимы, т.к. принадлежат видимым граням поверхности. Следовательно, прямая а до этих точек будет видима. На плоскости проекций П2 фронтальная проекция точки Е2 видима, т.к. лежит в видимой грани ЕL, а F2 невидима, т.к. лежит в невидимой грани ЕI (видимость граней на П2 определяется по горизонтальной проекции основания ΔЕ1L1I1х
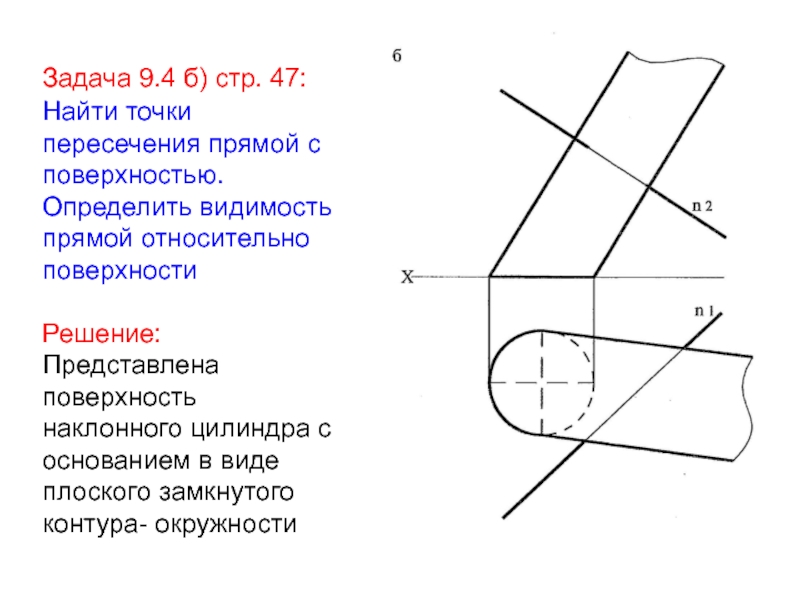
Слайд 15 Задача 9.4 б) стр. 47: Найти точки пересечения прямой с
поверхностью. Определить видимость прямой относительно поверхности Решение: Представлена поверхность наклонного цилиндра с
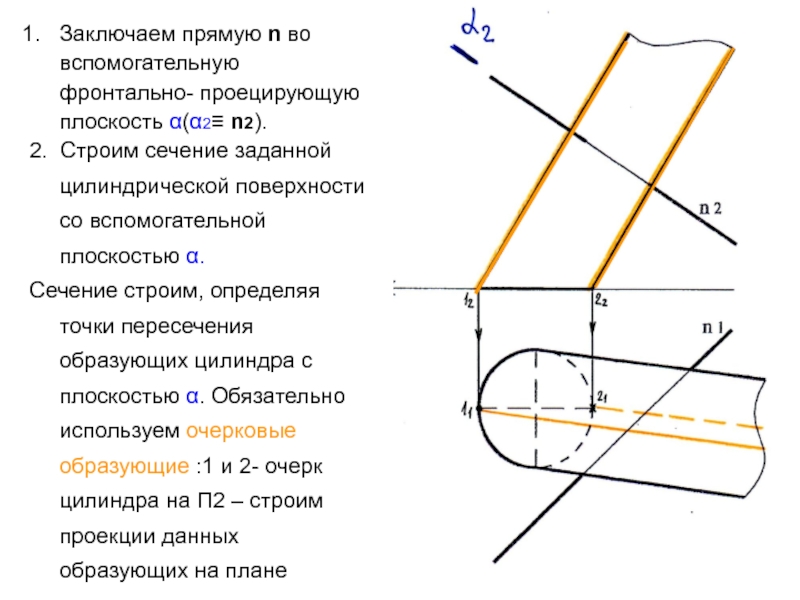
основанием в виде плоского замкнутого контура- окружностиСлайд 16Заключаем прямую n во вспомогательную фронтально- проецирующую плоскость α(α2≡ n2).
2.
Строим сечение заданной цилиндрической поверхности со вспомогательной плоскостью α.
Сечение строим,
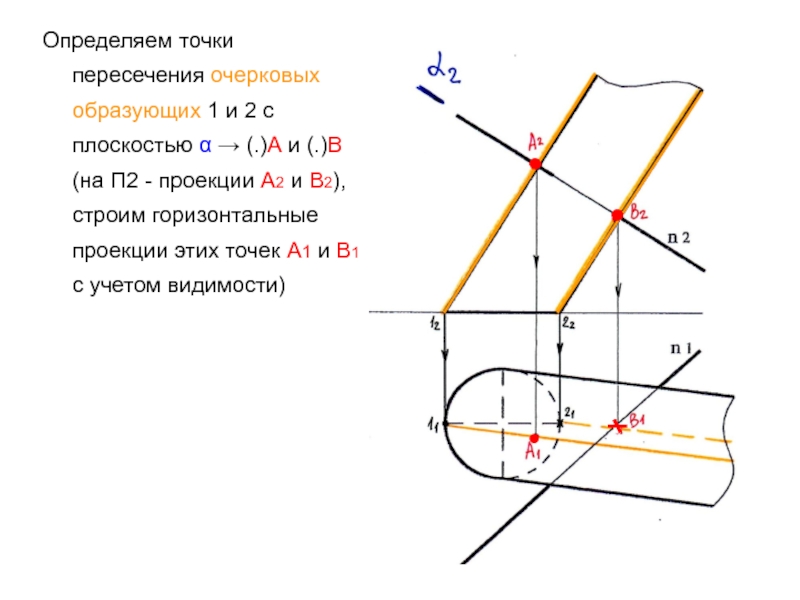
определяя точки пересечения образующих цилиндра с плоскостью α. Обязательно используем очерковые образующие :1 и 2- очерк цилиндра на П2 – строим проекции данных образующих на планеСлайд 17Определяем точки пересечения очерковых образующих 1 и 2 с плоскостью
α → (.)А и (.)В (на П2 - проекции А2
и В2), строим горизонтальные проекции этих точек А1 и В1 с учетом видимости)●
●
●
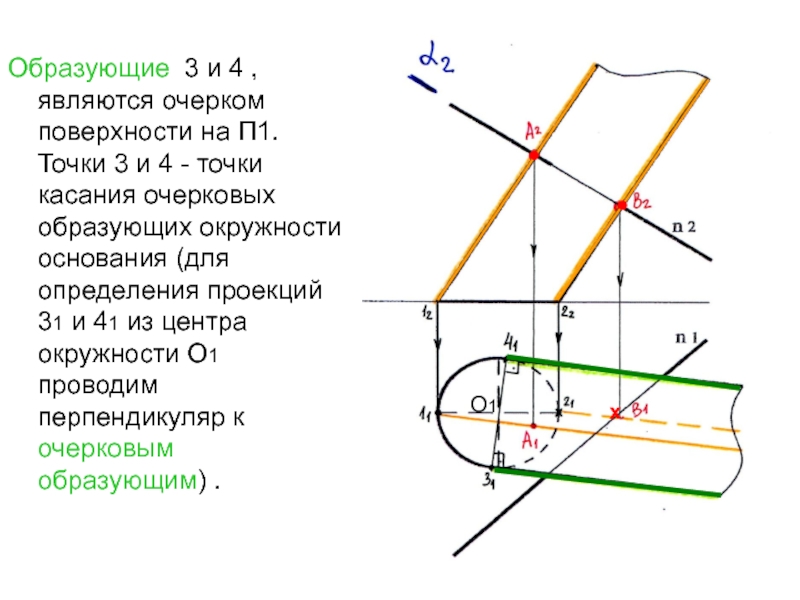
Слайд 18Образующие 3 и 4 , являются очерком поверхности на П1.
Точки 3 и 4 - точки касания очерковых образующих окружности
основания (для определения проекций 31 и 41 из центра окружности О1 проводим перпендикуляр к очерковым образующим) .О1
х
●
●
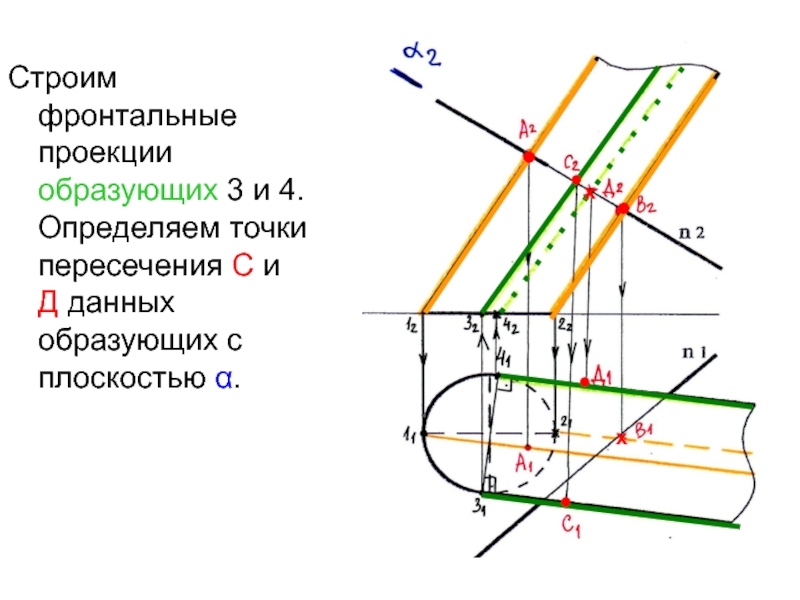
Слайд 19Строим фронтальные проекции образующих 3 и 4. Определяем точки пересечения
С и Д данных образующих с плоскостью α.
●
х
●
●
●
●
х
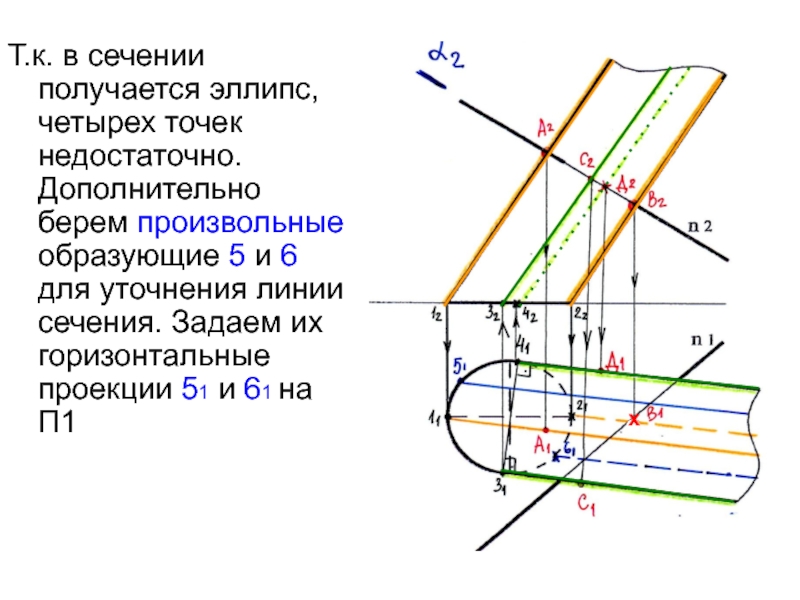
Слайд 20Т.к. в сечении получается эллипс, четырех точек недостаточно. Дополнительно берем
произвольные образующие 5 и 6 для уточнения линии сечения. Задаем
их горизонтальные проекции 51 и 61 на П1х
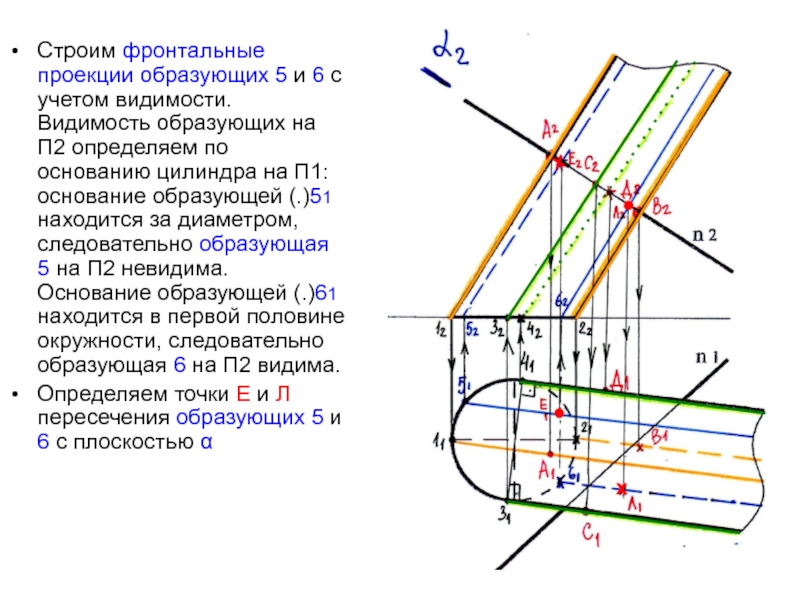
Слайд 21Строим фронтальные проекции образующих 5 и 6 с учетом видимости.
Видимость образующих на П2 определяем по основанию цилиндра на П1:
основание образующей (.)51 находится за диаметром, следовательно образующая 5 на П2 невидима. Основание образующей (.)61 находится в первой половине окружности, следовательно образующая 6 на П2 видима.Определяем точки Е и Л пересечения образующих 5 и 6 с плоскостью α
х
●
●
х
Слайд 22
4. Определяем видимость прямой.
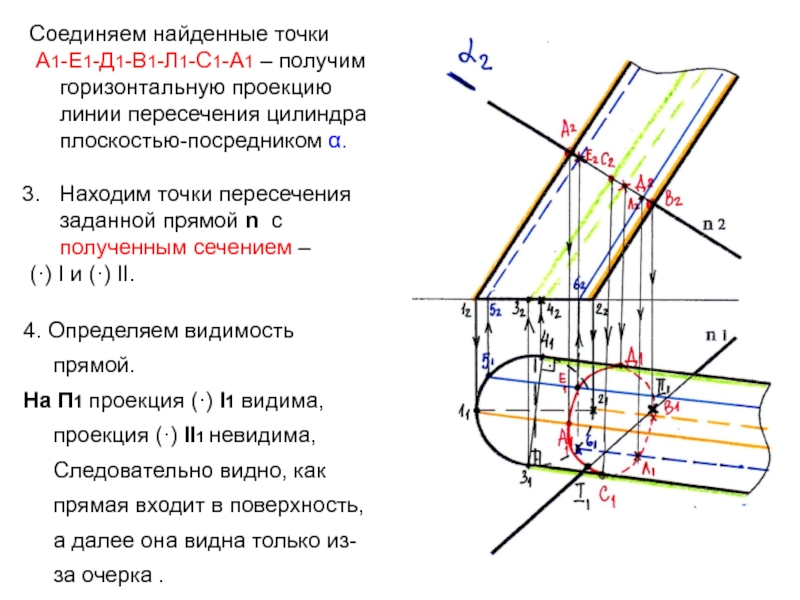
На П1 проекция (·) I1 видима,
проекция (·) II1 невидима, Следовательно видно, как прямая входит в
поверхность, а далее она видна только из-за очерка .Соединяем найденные точки
А1-Е1-Д1-В1-Л1-С1-А1 – получим горизонтальную проекцию линии пересечения цилиндра плоскостью-посредником α.
Находим точки пересечения заданной прямой n с полученным сечением –
(·) I и (·) II.
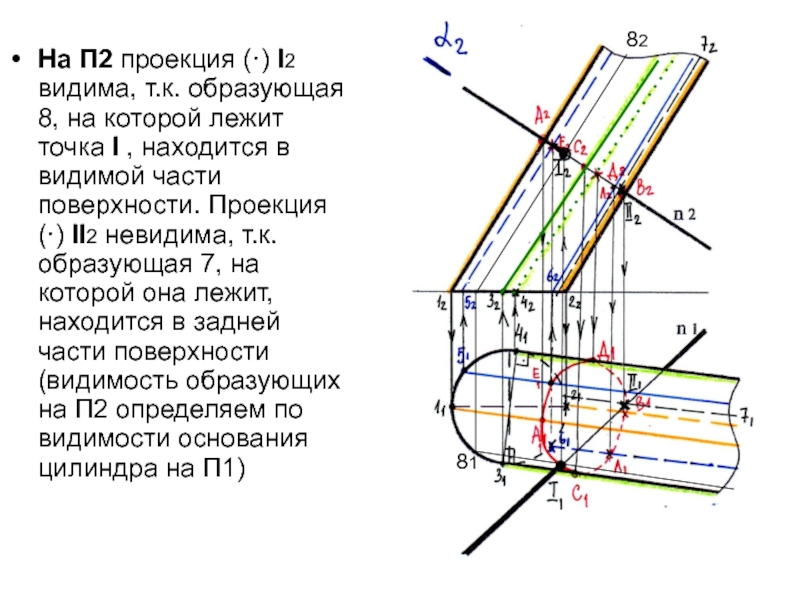
Слайд 23На П2 проекция (·) I2 видима, т.к. образующая 8, на
которой лежит точка I , находится в видимой части поверхности.
Проекция (·) II2 невидима, т.к. образующая 7, на которой она лежит, находится в задней части поверхности (видимость образующих на П2 определяем по видимости основания цилиндра на П1)81
82
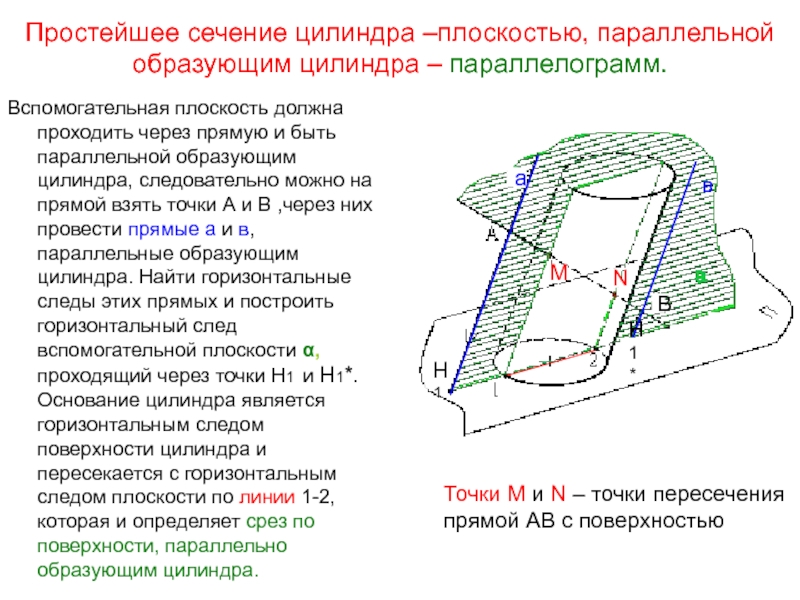
Слайд 24Простейшее сечение цилиндра –плоскостью, параллельной образующим цилиндра – параллелограмм.
Вспомогательная плоскость
должна проходить через прямую и быть параллельной образующим цилиндра, следовательно
можно на прямой взять точки А и В ,через них провести прямые а и в, параллельные образующим цилиндра. Найти горизонтальные следы этих прямых и построить горизонтальный след вспомогательной плоскости α, проходящий через точки Н1 и Н1*. Основание цилиндра является горизонтальным следом поверхности цилиндра и пересекается с горизонтальным следом плоскости по линии 1-2, которая и определяет срез по поверхности, параллельно образующим цилиндра.а
Н1
В
в
Н1*
Точки М и N – точки пересечения
прямой АВ с поверхностью
М
N
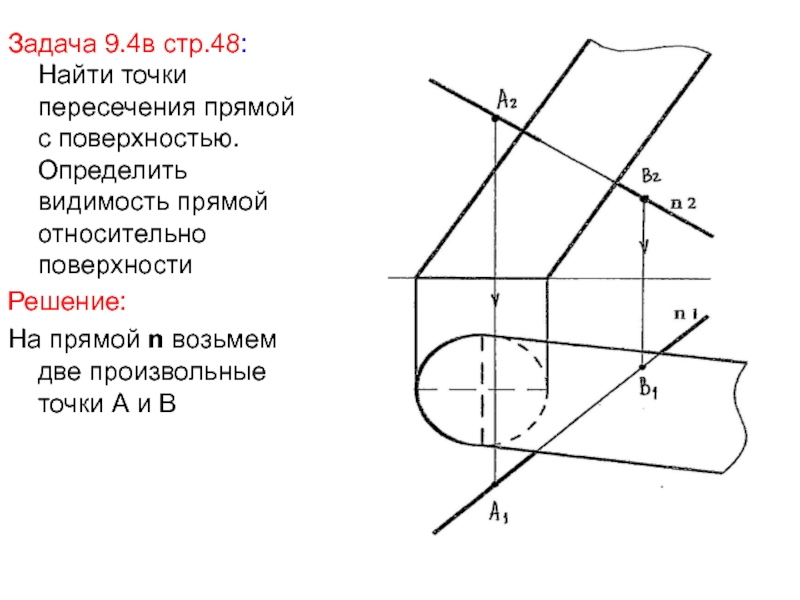
Слайд 25Задача 9.4в стр.48: Найти точки пересечения прямой с поверхностью. Определить
видимость прямой относительно поверхности
Решение:
На прямой n возьмем две произвольные точки
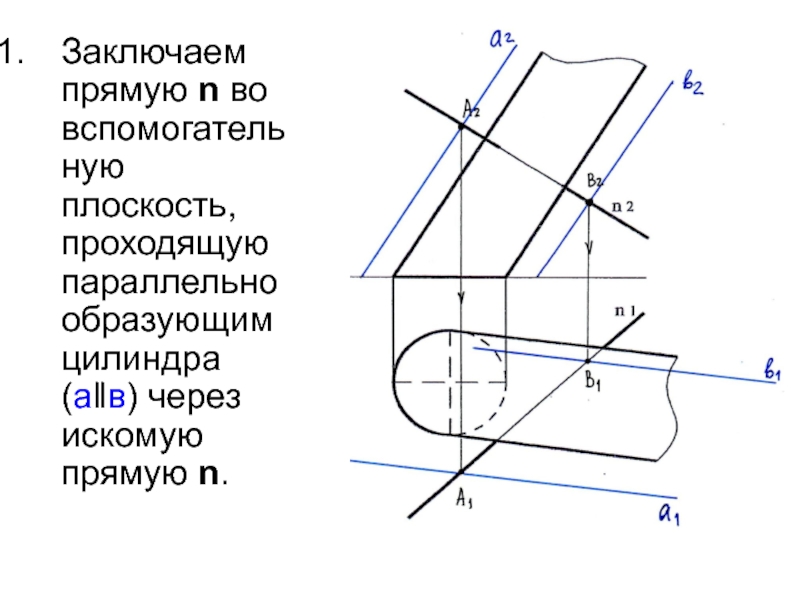
А и ВСлайд 26Заключаем прямую n во вспомогательную плоскость, проходящую параллельно образующим цилиндра
(а‖в) через искомую прямую n.
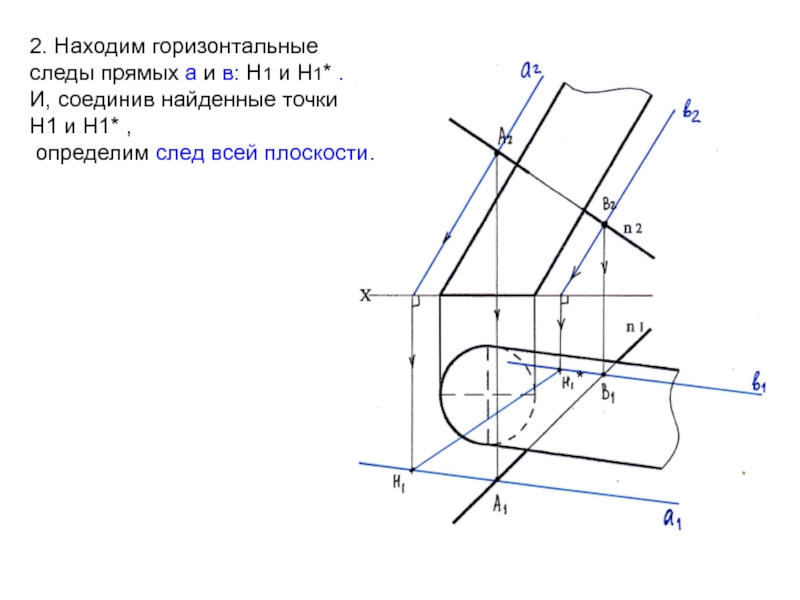
Слайд 272. Находим горизонтальные
следы прямых а и в: Н1 и
Н1* .
И, соединив найденные точки
Н1 и Н1* ,
определим
след всей плоскости.*
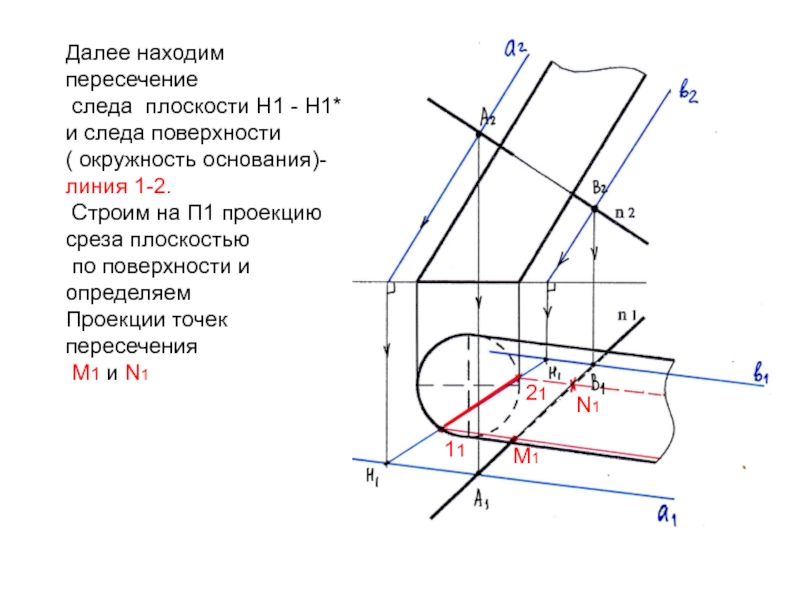
Слайд 28Далее находим пересечение
следа плоскости Н1 - Н1*
и следа
поверхности
( окружность основания)-
линия 1-2.
Строим на П1 проекцию
среза плоскостью
по поверхности и определяем
Проекции точек пересечения
М1 и N1
11
21
М1
N1
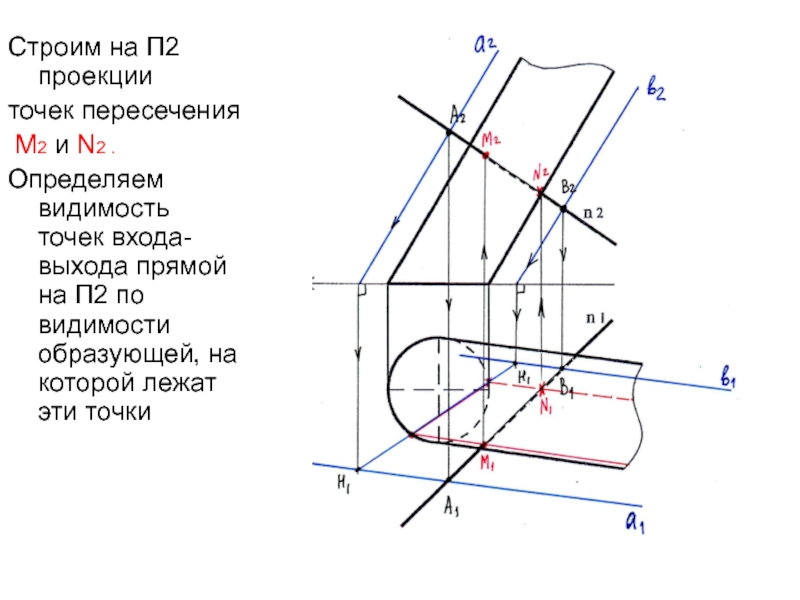
Слайд 29Строим на П2 проекции
точек пересечения
М2 и N2 .
Определяем
видимость точек входа-выхода прямой на П2 по видимости образующей, на
которой лежат эти точкиСлайд 31●
S
П1
●
А
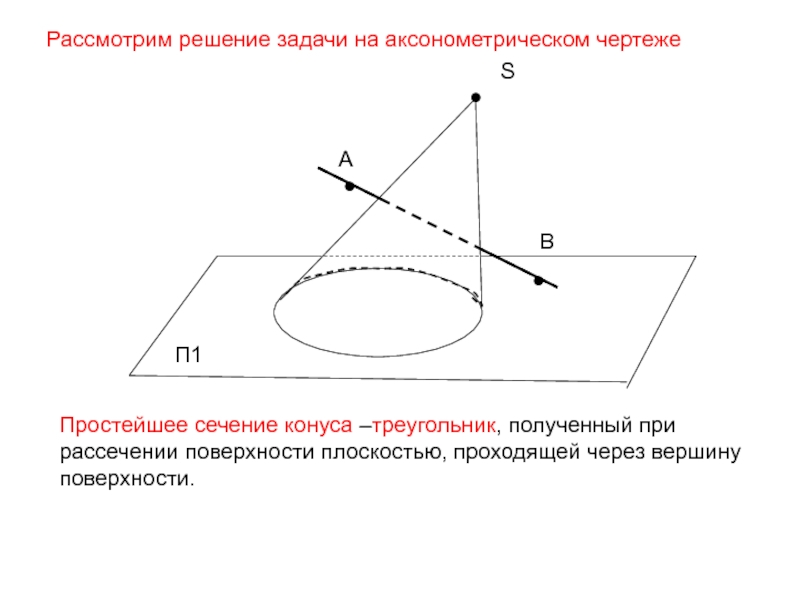
Простейшее сечение конуса –треугольник, полученный при рассечении поверхности плоскостью, проходящей
через вершину поверхности.
●
В
Рассмотрим решение задачи на аксонометрическом чертеже
Слайд 32●
S
П1
●
А
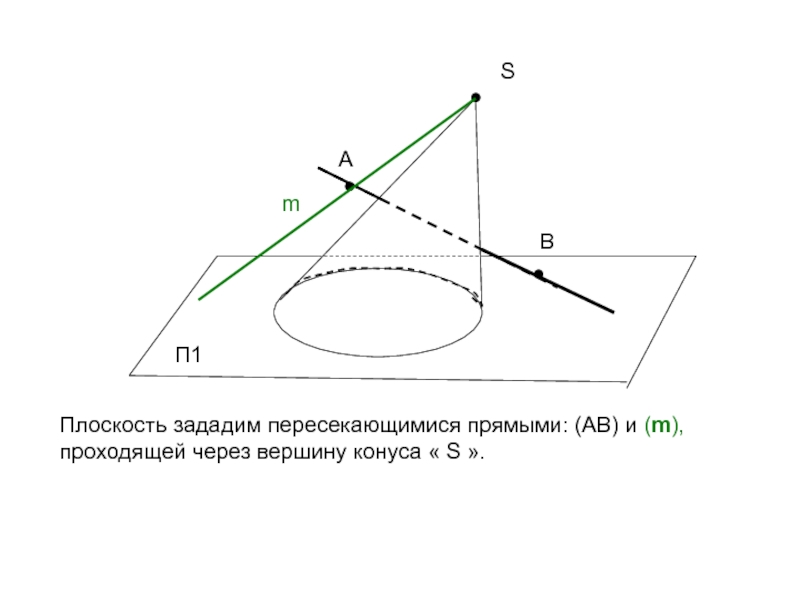
Плоскость зададим пересекающимися прямыми: (АВ) и (m), проходящей через вершину
конуса « S ».
●
В
m
Слайд 35●
S
П1
●
А
горизонтальный след плоскости и горизонтальный след поверхности пересекаются по линии
1-2 → построим сечение конуса, соединив найденные (..) 1 и
2 с вершиной конуса.●
В
m
●
Н1
Н1*
1
2
●
Слайд 37Простейшее сечение конуса и пирамиды –треугольник, полученный при рассечении поверхности
плоскостью, проходящей через вершину поверхности. Плоскость зададим пересекающимися прямыми: АВ
и m, проходящей через вершину конуса « S ».m2
m1
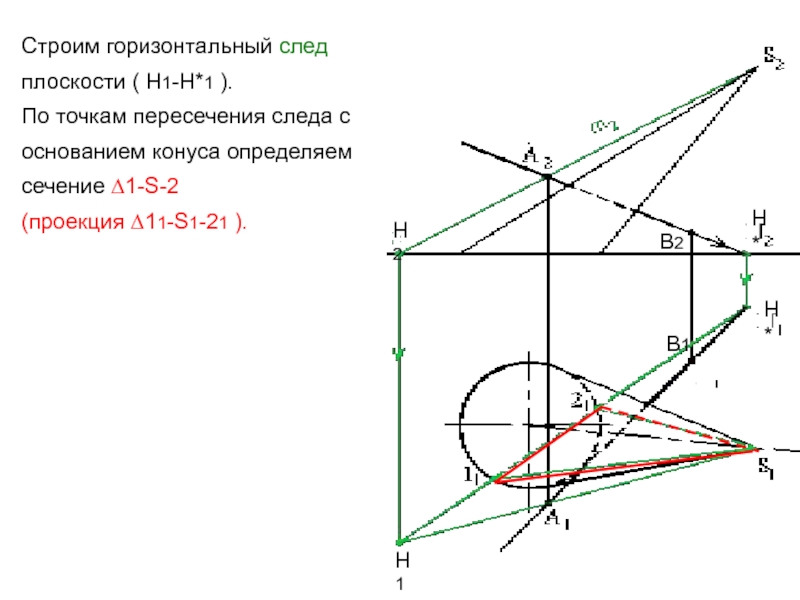
Слайд 38Строим горизонтальный след плоскости ( Н1-Н*1 ).
По точкам пересечения следа
с основанием конуса определяем сечение ∆1-S-2
(проекция ∆11-S1-21 ).
М
М
В2
В1
Н2
Н1
Н*
Н*
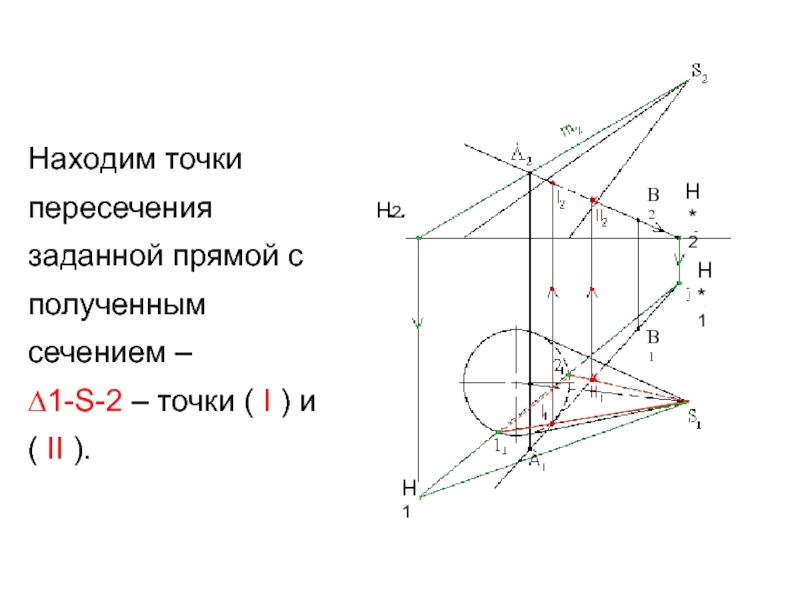
Слайд 39Находим точки пересечения заданной прямой с полученным сечением –
∆1-S-2
– точки ( I ) и ( II ).
М
М
В2
В1
х
х
Н2
Н1
Н*2
Н*1
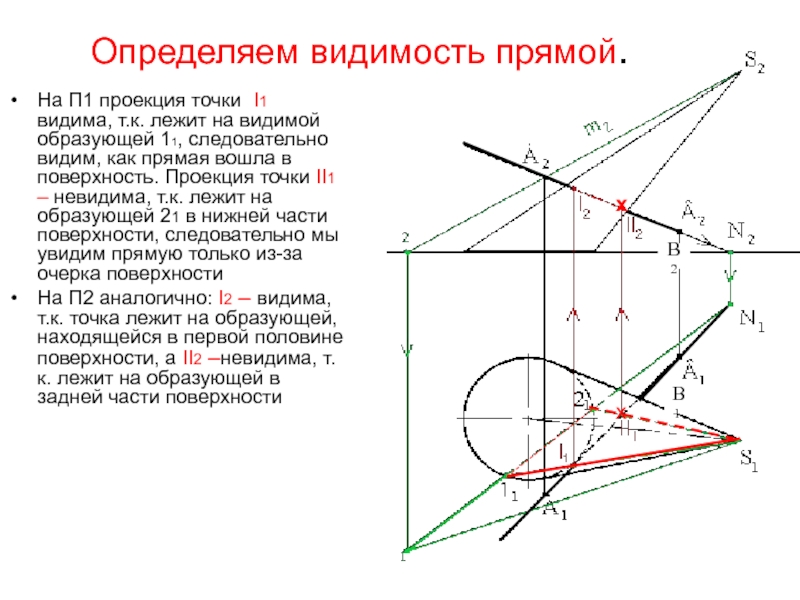
Слайд 40Определяем видимость прямой.
На П1 проекция точки I1 видима, т.к. лежит
на видимой образующей 11, следовательно видим, как прямая вошла в
поверхность. Проекция точки II1 – невидима, т.к. лежит на образующей 21 в нижней части поверхности, следовательно мы увидим прямую только из-за очерка поверхностиНа П2 аналогично: I2 – видима, т.к. точка лежит на образующей, находящейся в первой половине поверхности, а II2 –невидима, т.к. лежит на образующей в задней части поверхности
В2
В1
х
х
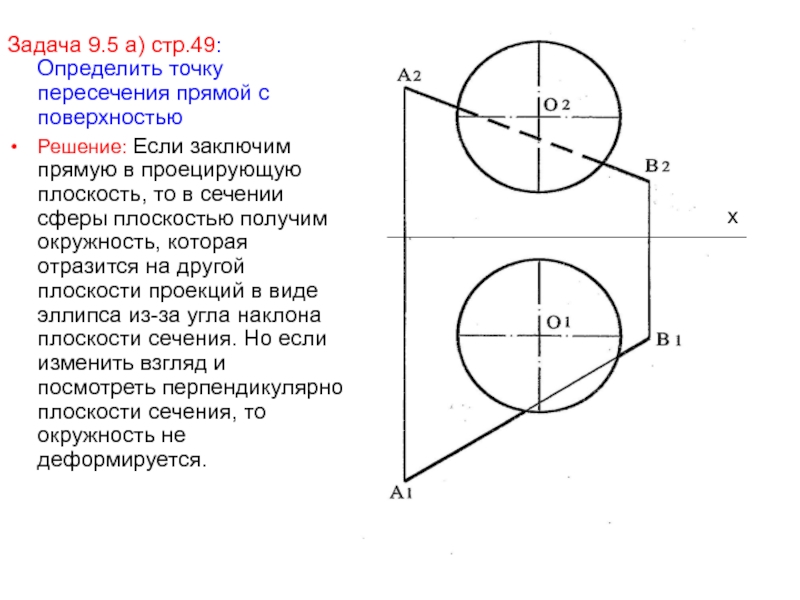
Слайд 41Задача 9.5 а) стр.49: Определить точку пересечения прямой с поверхностью
Решение:
Если заключим прямую в проецирующую плоскость, то в сечении сферы
плоскостью получим окружность, которая отразится на другой плоскости проекций в виде эллипса из-за угла наклона плоскости сечения. Но если изменить взгляд и посмотреть перпендикулярно плоскости сечения, то окружность не деформируется.х
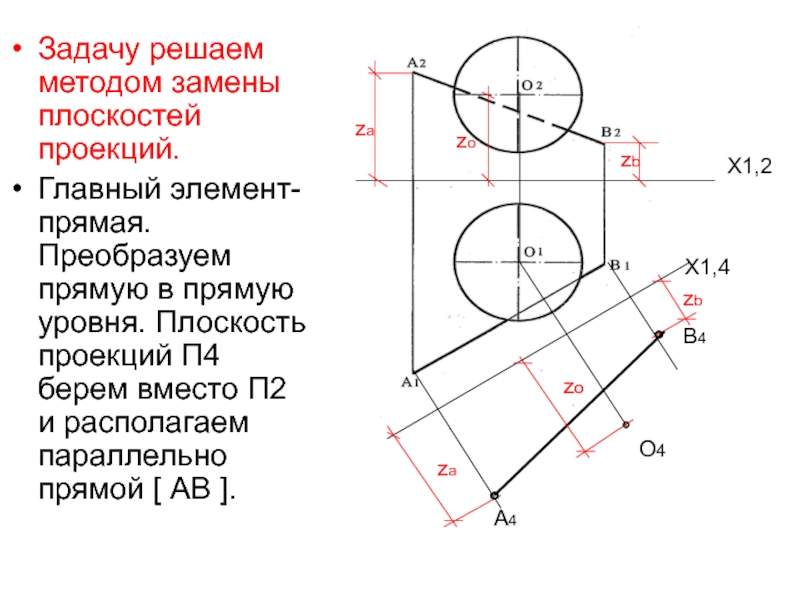
Слайд 42Задачу решаем методом замены плоскостей проекций.
Главный элемент- прямая. Преобразуем прямую
в прямую уровня. Плоскость проекций П4 берем вместо П2 и
располагаем параллельно прямой [ АВ ].Х1,2
Х1,4
zb
zb
B4
°
za
za
A4
°
zo
zo
°
O4
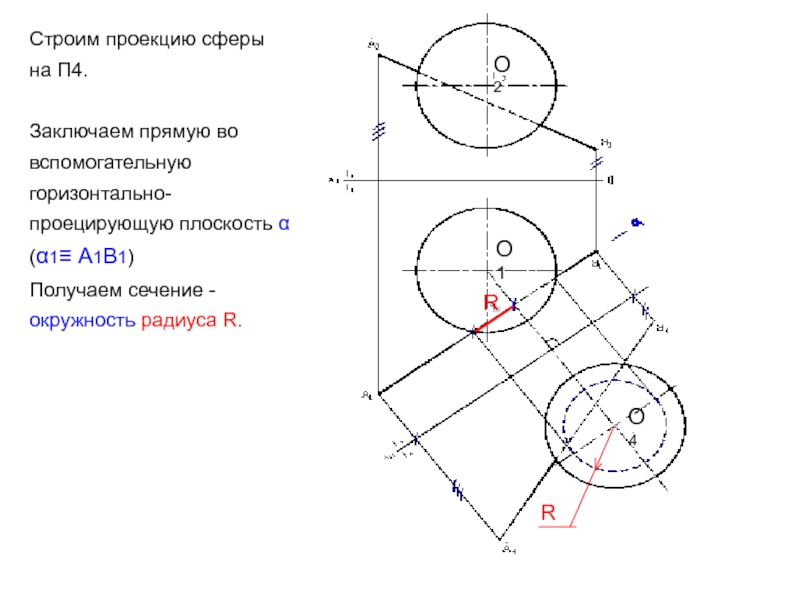
Слайд 43Строим проекцию сферы на П4.
Заключаем прямую во вспомогательную горизонтально-проецирующую плоскость
α (α1≡ А1В1)
Получаем сечение - окружность радиуса R.
О2
О1
О4
R
R
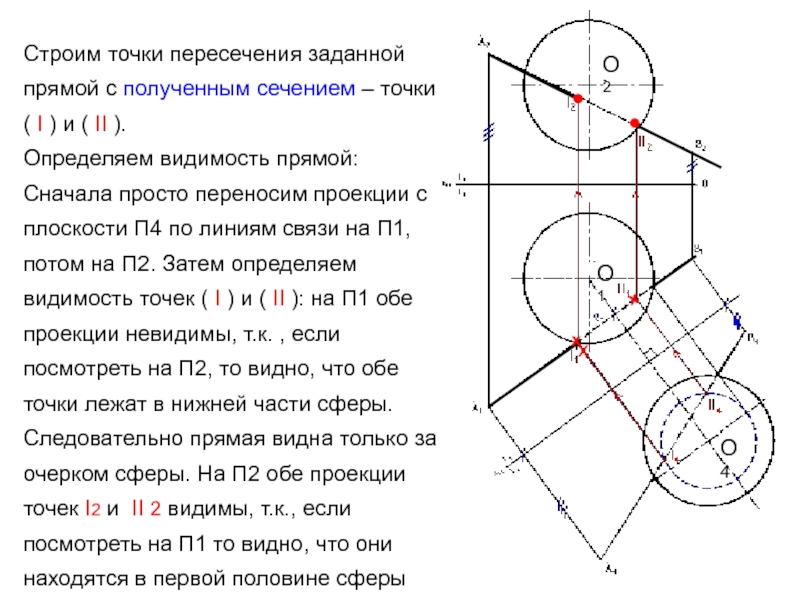
Слайд 44Строим точки пересечения заданной
прямой с полученным сечением – точки
( I
) и ( II ).
Определяем видимость прямой:
Сначала просто переносим
проекции с плоскости П4 по линиям связи на П1, потом на П2. Затем определяем видимость точек ( I ) и ( II ): на П1 обе проекции невидимы, т.к. , если посмотреть на П2, то видно, что обе точки лежат в нижней части сферы. Следовательно прямая видна только за очерком сферы. На П2 обе проекции точек I2 и II 2 видимы, т.к., если посмотреть на П1 то видно, что они находятся в первой половине сферыО2
О1
О4
x
x
x
●
●