Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 8
Содержание
- 1. Лекция 8
- 2. ПредпосылкаЕстественный язык не может использоваться для записи алгоритма в силу его:изменчивости;неоднозначности;избыточности
- 3. Опр.Формальный язык – это искусственный язык со
- 4. Опр.Формальная грамматика - система правил, описывающая множество конечных последовательностей символов формального алфавита.
- 5. Опр.Конечные цепочки символов называются предложениями формального языка,
- 6. Опр.Синтаксисом языка называются правила построения предложений языка. Синтаксис определяет множество формально правильных предложений
- 7. Опр.Семантикой языка называются правила интерпретации предложений языка (выбор значения из некоторого множества значений).Семантика определяется структурой предложения
- 8. Определение формальной грамматикиG = { Vn, Vt,
- 9. ПравилаVn ∩ Vt =0. Нетерминальный и терминальный
- 10. ПримерСловари Vn и Vt создаются с
- 11. Формальная грамматикаПоследовательность грамматических правил создается путем логических
- 12. ПоясненияПравило подстановок: если в преобразуемой цепочке есть
- 13. Пример 1 Дана грамматика G:Vn ={S};
- 14. Пример 2 Vt = {a,
- 15. Пример 2 Грамматика порождает язык, состоящий из
- 16. Пример 3Пусть Vt ={а,б,...,я, А,Б,...,Я} - множество
- 17. Разъяснение примера 2Грамматика порождает язык, состоящий из
- 18. Хомский выделил 4 типа грамматик1) Грамматики без
- 19. 2. Грамматика непосредственных составляющих Пример такой грамматики:SABA aA acB bB cb
- 20. 2. Грамматика непосредственных составляющихЧетыре вывода терминальных строк:
- 21. 3) Контекстно-свободные грамматикиВ левой части допускается лишь
- 22. 3) Контекстно-свободные грамматикиВыводы:S aT abT abcS aT
- 23. 4) Односторонние линейные грамматикиОни допускают подстановки вида: Аа А аb
- 24. Способы описания формальных языковДля описания языка-объекта должен
- 25. Способы описания формальных языковМетаязык должен быть сначала
- 26. Язык Бекуса-НаураНотации Бекуса-Наура (форма) (ФБН). Для формирования
- 27. Пример ФБН«идентификатор» На естественном языке: «Идентификатор -
- 28. Пример Записать определение арифметического выраженияVt = {А,
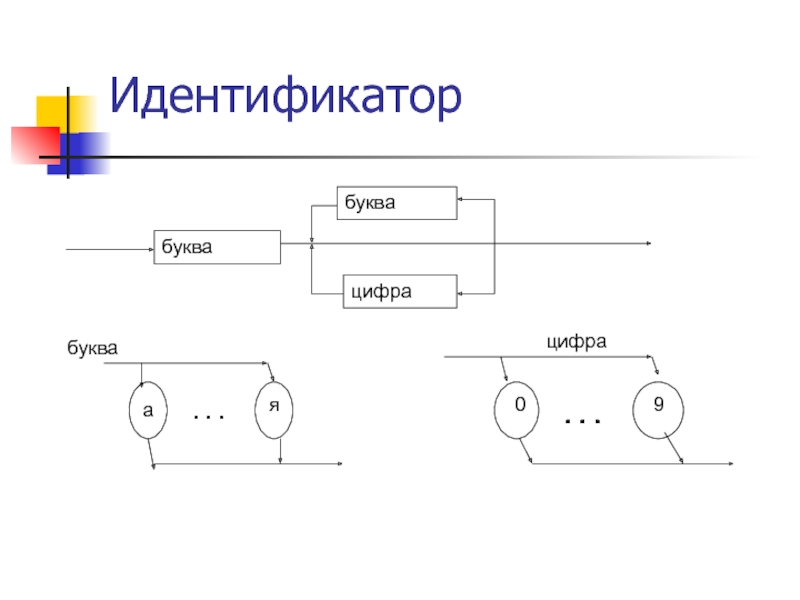
- 29. Синтаксические диаграммыСинтаксическая диаграмма - это схема (графическое
- 30. Идентификаторбуквабуквабуквабуквацифраая. . .буква09. . .цифра
- 31. Примеры 1. Опишите формальную грамматику, порождающую множество
- 32. ПримерыС помощью синтаксических диаграмм опишите следующие конструкции
- 33. Контрольные вопросыДайте определение формальной грамматики.Какие предложения допускает
- 34. Скачать презентанцию
ПредпосылкаЕстественный язык не может использоваться для записи алгоритма в силу его:изменчивости;неоднозначности;избыточности
Слайды и текст этой презентации
Слайд 1Лекция 8
Формальная грамматика.
Способы описания формальных языков. Мета-язык. Нотация Бекуса-Наура. Синтаксические
диаграммы
Слайд 2Предпосылка
Естественный язык не может использоваться для записи алгоритма в силу
его:
изменчивости;
неоднозначности;
избыточности
Слайд 3Опр.
Формальный язык – это искусственный язык со строгим синтаксисом и
полной смысловой определенностью.
Любой конечный механизм задания языка называется грамматикой
Разработка формальных грамматик была начата Хомским.
Слайд 4Опр.
Формальная грамматика - система правил, описывающая множество конечных последовательностей символов
формального алфавита.
Слайд 5Опр.
Конечные цепочки символов называются предложениями формального языка, а само множество
цепочек - языком, описываемым данной грамматикой.
Слайд 6Опр.
Синтаксисом языка называются правила построения предложений языка.
Синтаксис определяет множество
формально правильных предложений
Слайд 7Опр.
Семантикой языка называются правила интерпретации предложений языка (выбор значения из
некоторого множества значений).
Семантика определяется структурой предложения
Слайд 8Определение формальной грамматики
G = { Vn, Vt, P, S} ,
где
Vn – нетерминальный словарь
Vt - терминальный словарь
P
– множество правил подстановок имеющие вид g -> h, где g и h - цепочки, состоящие из терминальных и нетерминальных символов. S Vn - аксиома, начальный знак.
Слайд 9Правила
Vn ∩ Vt =0.
Нетерминальный и терминальный словари являются непересекающимися
множествами
их объединение определяет словарь символов языка V=Vn U Vt .
Слайд 10Пример
Словари Vn и Vt создаются с помощью знаков алфавита.
Последовательное применение правил порождает все возможные слова, входящие в терминальный
словарь. Нетерминальный словарь в состав языка не включается.P1: S ab и P2:S aSb порождают язык L={ab, aabb, a3b3, …}
Слайд 11Формальная грамматика
Последовательность грамматических правил создается путем логических заключений.
Процесс создания
языка начинается с аксиомы – исходного набора знаков, к которому
затем применяются одно за другим установленные правила подстановки.Таким образом, из небольшого набора исходных конструкций порождаются все допустимые их комбинации
Слайд 12Пояснения
Правило подстановок: если в преобразуемой цепочке есть слово g, то
оно заменяется словом h.
Получение на некотором шаге цепочки, состоящей
только из терминальных символов, свидетельствует о прекращении процесса порождения - эта цепочка является правильной, завершенной конструкцией порождаемого языка. Слайд 13Пример 1
Дана грамматика G:
Vn ={S}; Vt ={*,0}; P={S→SS; S→*;
S→*S0}
Порожденным такой грамматикой языком L(G) будет
L = {*, **, ***0,
***0**0, … }.Слайд 15Пример 2
Грамматика порождает язык, состоящий из всех «слов-перевертышей» в алфавите
{a, b}, имеющих нечетную длину, например, aba, abababa, bbbbb, baaaaaab
и т.д.Цепочки типа αSα-1, где α-1 означает слово α, записанное справа налево
Слайд 16Пример 3
Пусть Vt ={а,б,...,я, А,Б,...,Я} - множество терминальных символов -
букв русского алфавита.
Vn = {Q, R, S} - нетерминальный
словарь, где Q = {q1,..,.qn} - множество имен людей в русском алфавите,R = {r1,…,.rm} - множество глаголов, стоящих в третьем лице единственного числа настоящего времени.
Система подстановок :
S → QR
Q → q1, Q → q2, …, Q → qm
R→ r1, R→ r2, …, R→ rm
Слайд 17Разъяснение примера 2
Грамматика порождает язык, состоящий из фраз типа: «такой-то
делает то-то», например, «Маша читает», «Вася спит» и т.п. Работает
грамматика следующим образом: на первом шаге определяется тип фразы; второй шаг порождает конкретное имя, а третий шаг - конкретное действие (глагол).Слайд 18Хомский выделил 4 типа грамматик
1) Грамматики без ограничений.
а) аАвСД
aНД
Порождение АвС H возможно только в контексте а .... Д.б) PQ QP
Свобода выбора перестановок.
Грамматики без ограничений не представляют интереса с точки зрения информатики - слишком много свободы.
Слайд 202. Грамматика непосредственных составляющих
Четыре вывода терминальных строк:
S AB aB
ab
S AB acB acb
S AB aB acb
S ABacB accb
2
и 3 –я строки двусмысленныСлайд 213) Контекстно-свободные грамматики
В левой части допускается лишь один нетерминальный символ
(не зависит от контекста)
Пусть задана грамматика
S aT T bT
T c
Слайд 223) Контекстно-свободные грамматики
Выводы:
S aT abT abc
S aT abT abbTabbc
Данная грамматика
содержит рекурсивное правило подстановки: ас, аbс, аbbс, аbbbс, ....., в
общем виде abnc (n>=0).Слайд 24Способы описания формальных языков
Для описания языка-объекта должен применяться метаязык.
Метаязык
должен обладать некоторыми свойствами формального языка, чтобы однозначно определять конструкции
языка-объектаСлайд 25Способы описания формальных языков
Метаязык должен быть сначала описан сам.
Для
описания любого метаязыка можно использовать язык естественный.
Таким образом, для
построения формального языка необходимо средствами естественного языка описать метаязык, а затем посредством метаязыка описать язык формальный Слайд 26Язык Бекуса-Наура
Нотации Бекуса-Наура (форма) (ФБН).
Для формирования предложений используются метасимволы:
{ , ::=, | }.
Угловые скобки - служат
для обрамления нетерминального символа. Символ «::=» читается «по определению есть»;
символ «|» - «или».
Слайд 27Пример ФБН
«идентификатор»
На естественном языке: «Идентификатор - это любая последовательность
букв и цифр, начинающаяся с буквы».
В форме Бекуса-Наура :
::=|
|<идентификатор><цифра><буква>::= а|b|c|…
<цифра>::= 0|1|2|3|...|9.
Слайд 28Пример
Записать определение арифметического выражения
Vt = {А, С, +, -
},
::= АС
::=+-
А, С, А+С, С+А, А-С, С-А, А+А, А-А,
С+С, С-ССлайд 29Синтаксические диаграммы
Синтаксическая диаграмма - это схема (графическое представление) описания какого-либо
нетерминального символа языка-объекта.
Схема всегда имеет один вход и один
выход. Элементами схемы могут служить терминальные символы языка-объекта, заключенные в окружность (или овал) или нетерминальные символы (понятия) языка-объекта, заключенные в прямоугольник. Слайд 31Примеры
1. Опишите формальную грамматику, порождающую множество целых двоичных чисел.
2. Измените
описание грамматики из примера таким образом, чтобы она
описывала конструкции типа «Имя_1, Имя_2.. Имя М делают_то-то».3. Что определяет следующая нотация Бекуса-Наура: <формула>::=<цифра>|(<формула><знак><формула>) <знак>::= +| — | *
<цифра>::= 0|1|2|3|4|5|6|7|8|9
Слайд 32Примеры
С помощью синтаксических диаграмм опишите следующие конструкции языка PASCAL:
1. оператор
цикла с предусловием WHILE...DO;
2. составной оператор;
3. оператор цикла с параметром
FOR...DO;4. оператор выбора CASE.












































![Семья Кузнецовых до революции. [1915-1916 гг. ]](/img/tmb/7/626275/071fbcc85ae02e069986bef54586a52a-800x.jpg)