Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция № 10
Содержание
- 1. Лекция № 10
- 2. Қисық сызық туралы түсінікСызықтар түзу сызық және
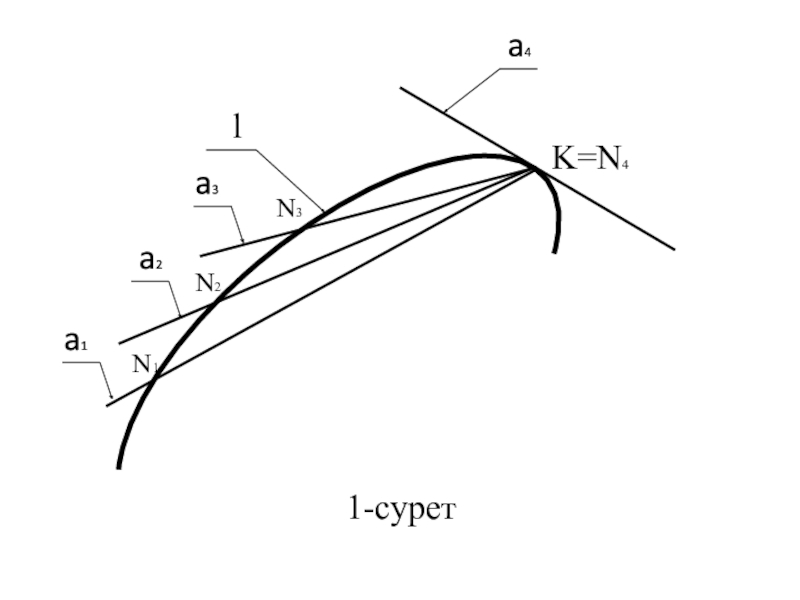
- 3. a4a2a1a3K=N4N1N3N2l1-сурет
- 4. 1- суретl сызығының a жанама түзуінің К
- 5. Қисық сызықтар туралы түсінікЕкінші ретті қисықтар: шеңбер,
- 6. Қисық сызықтар туралы түсінікЕгер қисық сызықтың кез
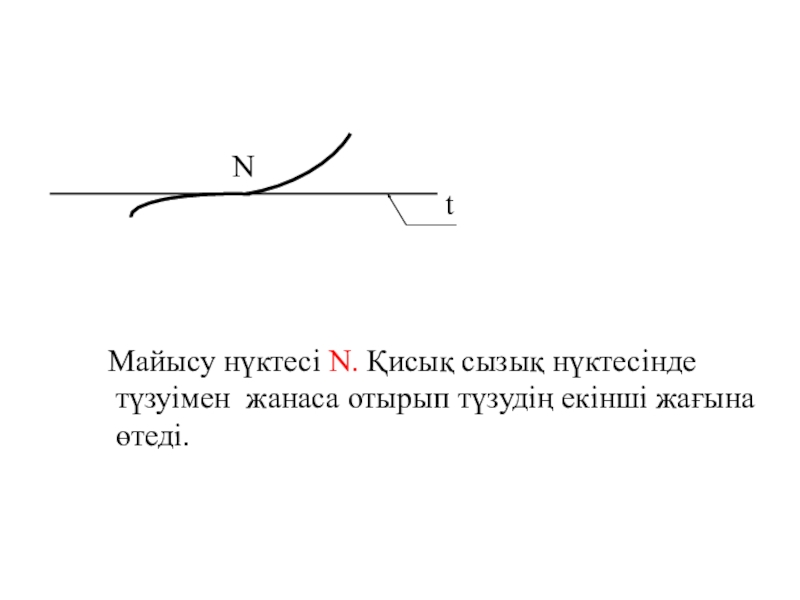
- 7. tNМайысу нүктесі N. Қисық сызық нүктесінде түзуімен жанаса отырып түзудің екінші жағына өтеді.
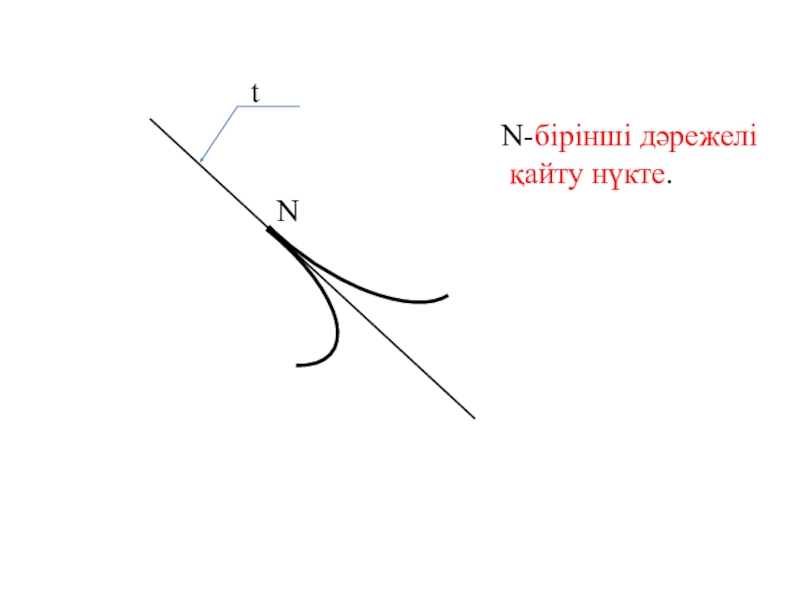
- 8. tNN-бірінші дәрежелі қайту нүкте.
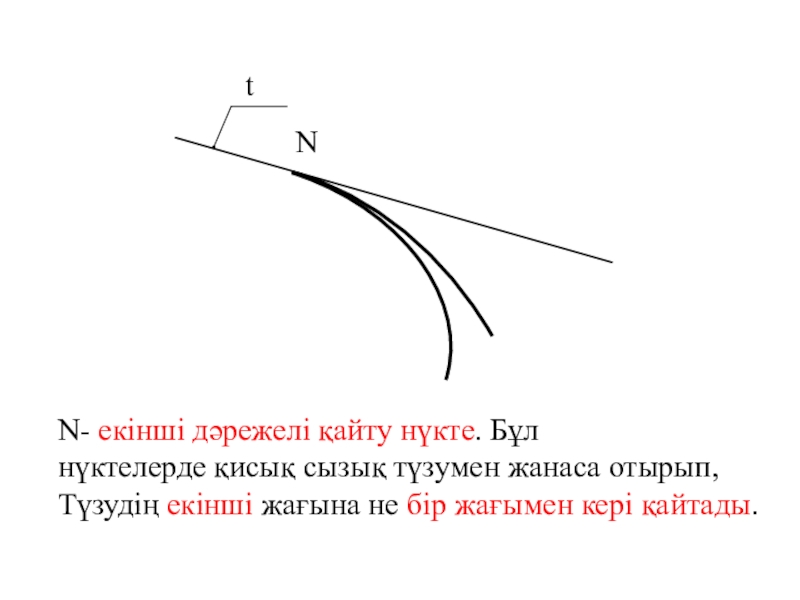
- 9. tNN- екінші дәрежелі қайту нүкте. Бұл нүктелерде
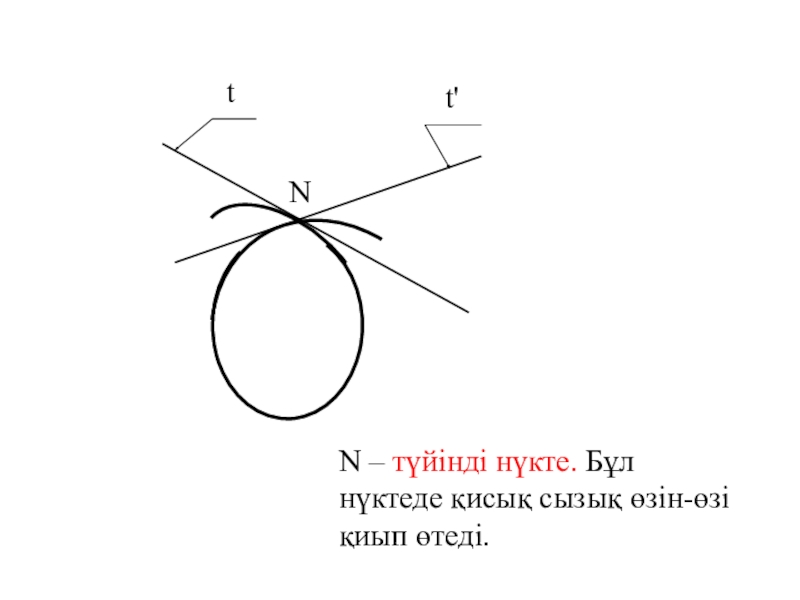
- 10. Ntt'N – түйінді нүкте. Бұл нүктеде қисық сызық өзін-өзіқиып өтеді.
- 11. Беттер және олардың анықтауштары
- 12. Цилиндрлік бет.
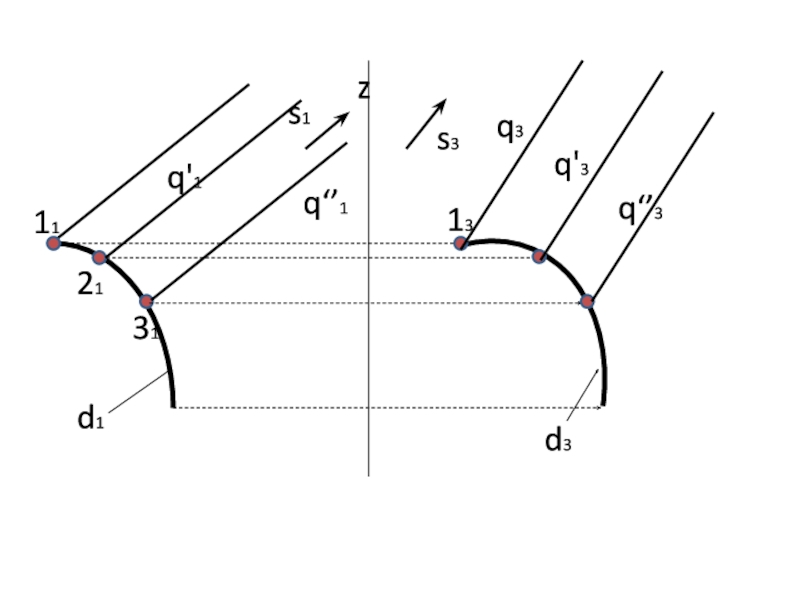
- 13. zd1d3s1s3q'11113q321q'331q‘’3q‘’1
- 14. Слайд 14
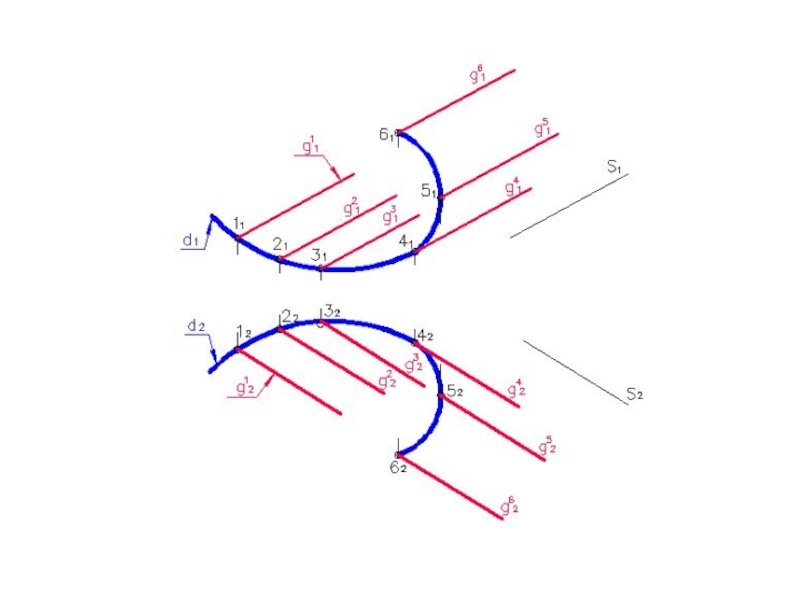
- 15. Конустық бет
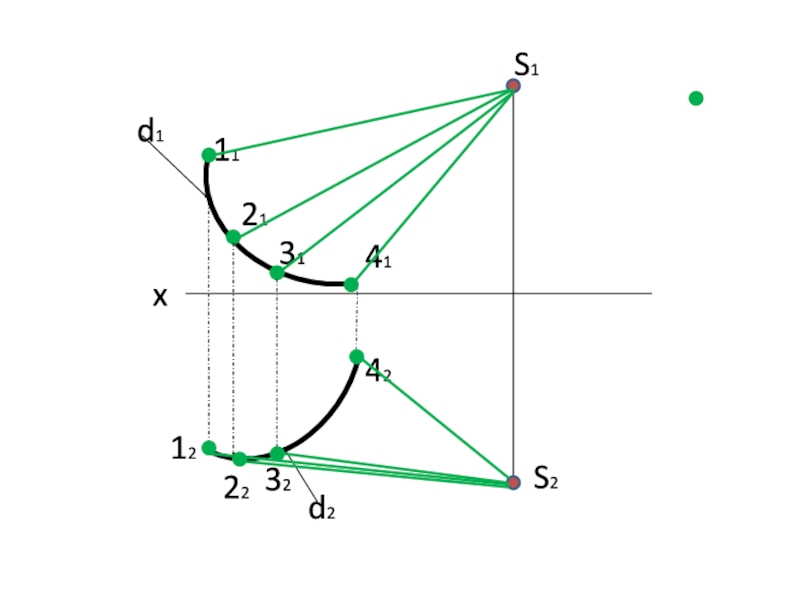
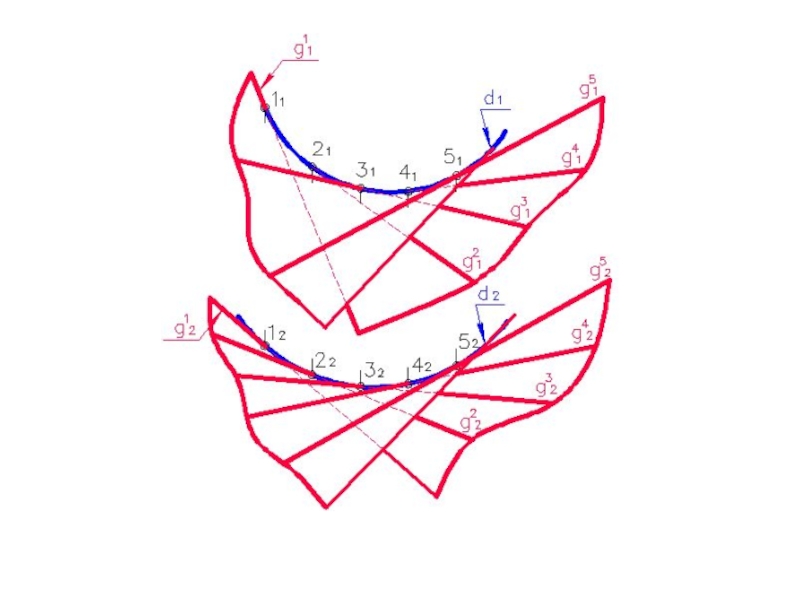
- 16. xS2S1d1d21112322221414231
- 17. Слайд 17
- 18. Кері қайту қыры бар қисық бетАнықтаушы:ω (q,
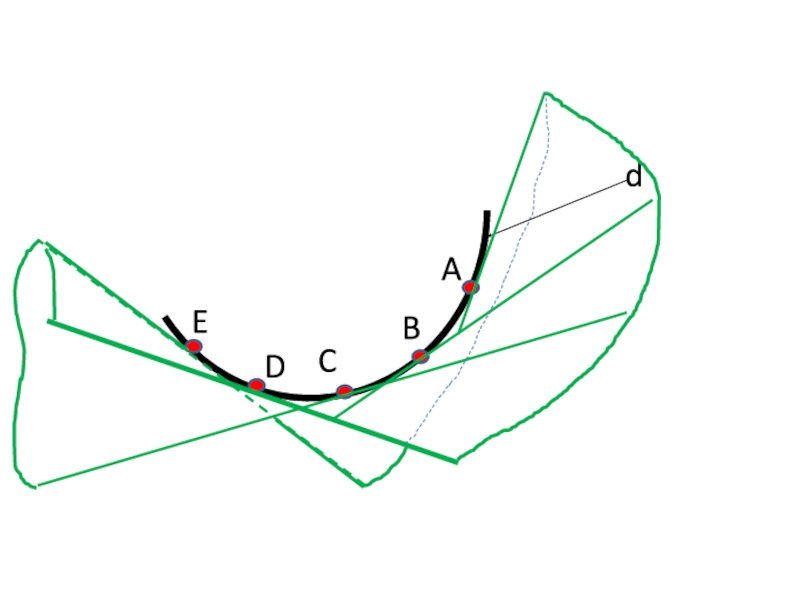
- 19. dABDEC
- 20. Слайд 20
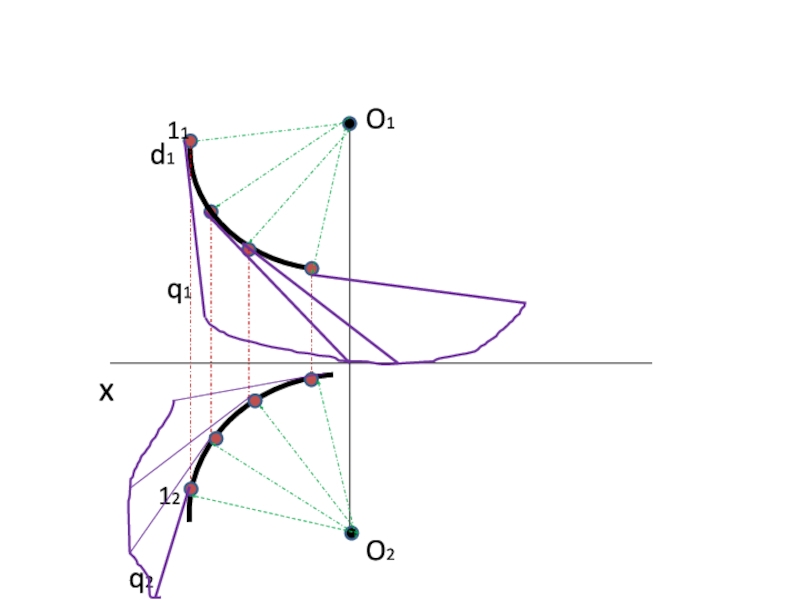
- 21. xO2O1d111q112q2
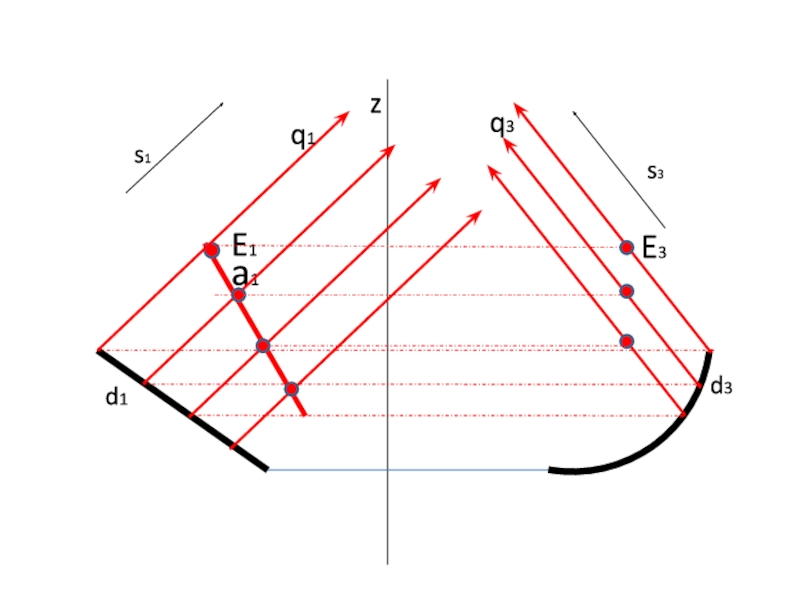
- 22. zd1d3s1s3a1E1q1q3E3
- 23. Скачать презентанцию
Қисық сызық туралы түсінікСызықтар түзу сызық және қисық сызық болып екіге бөлнеді.Қисық сызық кеністікте үздіксіз қозғалыстағы нүктенің траекториясы ретінде қарастырылады.Сызықтағы нүктенің қозғалыс бағыты сол нүктеден сызыққа жүргізілген жанамамен анықталады.
Слайды и текст этой презентации
Слайд 2Қисық сызық туралы түсінік
Сызықтар түзу сызық және қисық сызық болып
екіге бөлнеді.
нүктенің қозғалыс бағыты сол нүктеден сызыққа жүргізілген жанамамен анықталады.
Слайд 41- сурет
l сызығының a жанама түзуінің К нүктесіндегі жағдайы қиюші
түзудің шекті жағдайы деп аталады (сызықтың N нүктесі K нүктесіне
ұмтылады).Қисық сызықтар жазық және кеңіс сызықтары болып екіге бөлнеді. Жазық қисық сызықтардың барлық нүктелері бір жазықтықта жатады.
Слайд 5Қисық сызықтар туралы түсінік
Екінші ретті қисықтар: шеңбер, эллипс, гипербола, парабола,
т.с.с. жазық қисық сызықтарға жатады.
Қисық сызықтар математика теңдеуімен және графика
түрінде беріледі. Кейде математика тендеуімен берілген қисық сызықты заңды, ал графикалы берілген қисық сызықты заңсыз деп атайды.
Слайд 6Қисық сызықтар туралы түсінік
Егер қисық сызықтың кез келген нүктесі тек
жалғыз жанама түзуі болса онда оны тегіс қисық сызық дейді
(1 сурет). Мұндай қисық сызықтың барлық нүктелерің қарапайым нүктелер дейді.Сонымен қатар қисық сызықтарда ерекше нүктелер болады.
Слайд 7t
N
Майысу нүктесі N. Қисық сызық нүктесінде
түзуімен жанаса отырып
түзудің екінші жағына
өтеді.
Слайд 9t
N
N- екінші дәрежелі қайту нүкте. Бұл
нүктелерде қисық сызық түзумен
жанаса отырып,
Түзудің екінші жағына не бір жағымен кері қайтады.
Слайд 18Кері қайту қыры бар қисық бет
Анықтаушы:
ω (q, d) {q
d }
q – жасаушы түзу;
d- бағыттаушы қисық сызық.
