Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция № 8-9 Дисперсионный анализ результатов опыта
Содержание
- 1. Лекция № 8-9 Дисперсионный анализ результатов опыта
- 2. Дисперсионный анализ в биологических исследованиях впервые введен
- 3. В опытах с удобрениями применяют не менее
- 4. При проведении полевых и вегетационных опытов с
- 5. Систематические ошибки - в полевом опыте обусловлены
- 6. Грубые ошибки - возникают в результате нарушения
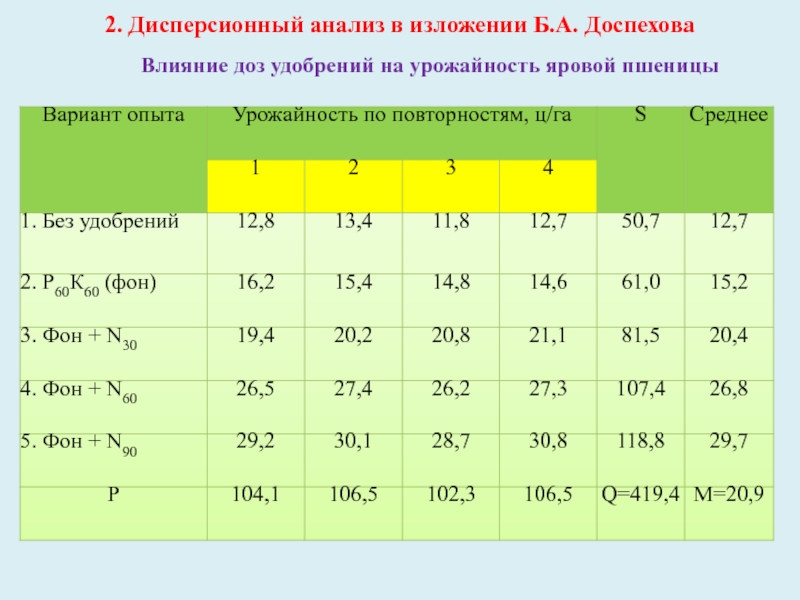
- 7. 2. Дисперсионный анализ в изложении Б.А. Доспехова Влияние доз удобрений на урожайность яровой пшеницы
- 8. Выбирают произвольное начало, за которое берут среднее
- 9. Квадраты отклонений урожая от произвольного начала
- 10. Слайд 10
- 11. Далее определяют:сумму квадратов общего рассеяния по формуле
- 12. При проведении статистической обработки методом анализа рассеяния
- 13. Остаточное рассеяние (Cz) получают путем вычитания из
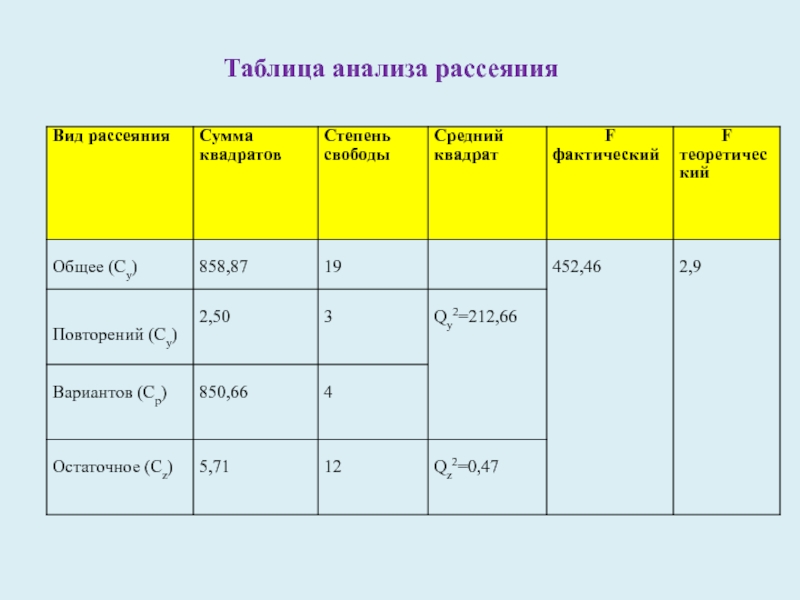
- 14. Таблица анализа рассеяния
- 15. Для установления достоверности действия изучаемых в опыте
- 16. F таб находят в таблицах
- 17. Для определения относительной ошибки (точности опыта) и
- 18. Подставляя значение Sα в формулу НСР НСР
- 19. Слайд 19
- 20. Величина НСР 0,5 используется при сравнении вариантов
- 21. 3 Корреляция и регрессия в агрохимических исследованиях
- 22. Под прямолинейной корреляцией понимают такую зависимость, когда
- 23. Пример установления прямолинейной зависимости между урожайностью яровой
- 24. Коэффициент корреляции является безмерной
- 25. В нашем примере связь между урожайностью яровой
- 26. Какие ошибки сопровождают полевой опыт и как
- 27. Гмурман, В.Е. Теория вероятностей и математическая статистика
- 28. Скачать презентанцию
Дисперсионный анализ в биологических исследованиях впервые введен англ. ученым Р.А. Фишером. Основная цель анализа заключается в раскрытии смысла результатов эксперимента, т.е. в определении точности и достоверности исследований. В настоящее время предложено
Слайды и текст этой презентации
Слайд 1Лекция №8-9
Дисперсионный анализ результатов опыта
Понятие о дисперсионном анализе
Дисперсионный анализ в
изложении Б.А. Доспехова
Слайд 2Дисперсионный анализ в биологических исследованиях впервые введен англ. ученым Р.А.
Фишером.
Основная цель анализа заключается в раскрытии смысла результатов эксперимента,
т.е. в определении точности и достоверности исследований. В настоящее время предложено много модификаций метода Р.А. Фишера. В нашей стране наиболее распространены модификации В.Н. Перегудова и Б.А. Доспехова.В основе дисперсионного анализа (вариации) лежит предположение, что опыт достоверен тогда, когда рассеяние между вариантами (колебания урожайности) больше, чем между повторностями одного варианта.
Если изменения урожайности по делянкам от случайных причин превышают изменения, вызываемые факторами, изучаемыми в опыте (виды, формы и дозы удобрений), то такой опыт считается недостоверным.
Дисперсионный анализ позволяет экспериментатору определить степень влияния факторов в отдельности и суммарного их воздействия на изменчивость изучаемого признака. В опытах с удобрениями таким признаком является урожайность.
1. Понятие о дисперсионном анализе
Слайд 3В опытах с удобрениями применяют не менее трех повторений и
всегда высчитывают среднее из них.
В полевых опытах изменчивость поделяночных урожаев
обусловлена тремя факторами (причинами):действием изучаемого фактора (удобрения) - рассеяние по вариантам;
плодородием почвы каждого повторения - рассеяние по повторностям;
случайными причинами (неточность измерений, неравномерность посевов) - остаточное рассеяние.
Таким образом, на результатах любого сельскохозяйственного опыта помимо изучаемого фактора сказываются пестрота почвенного плодородия, неоднородность действия агротехнических приемов, индивидуальные особенности растений, а также ошибки, возникающие при использовании несовершенных измерительных приборов, машин и техники.
Слайд 4При проведении полевых и вегетационных опытов с удобрениями всегда наблюдается
варьирование урожаев параллельных делянок и вегетационных сосудов одноименных вариантов. Причиной
такого варьирования являются разного рода ошибки.Различают случайные, систематические и грубые ошибки.
Случайные ошибки - это ошибки, возникающие в результате неоднородности почвенного плодородия, индивидуальной изменчивости растений, случайных механических повреждений растений, поражения растений болезнями. Таких ошибок полностью избежать не удается; при соблюдении всех агротехнических приемов и требований при постановке опыта их можно свести к минимуму.
Слайд 5Систематические ошибки - в полевом опыте обусловлены различным плодородием почвы
опытного участка. Они завышают или занижают урожайность.
Различают три типа
систематической ошибки: сплошная (захватывает все варианты всех повторений опыта)
При сплошной систематической ошибке сравнимость результатов не нарушается, хотя сами результаты получаются завышенными или заниженными.
захватывающая все варианты одного или нескольких повторений
Определяется различным плодородием почвы разных повторений опыта, при статистической обработке исключается из общего варьирования.
затрагивающая лишь некоторые варианты
Нарушает сравнимость вариантов, делает результаты опыта недостоверными.
Для того, чтобы избежать систематической ошибки, необходимо детальное почвенное и агрохимическое обследование участка, проведение уравнительных на новом месте) и рекогносцировочных (после применения хим. препаратов) посевов.
Слайд 6Грубые ошибки - возникают в результате нарушения основных требований к
полевому опыту. Примером грубой ошибки могут служить внесение на делянку
неверно рассчитанной дозы удобрений или внесение удобрений дважды на одну делянку, высев на делянке семян другого сорта и т.д. Такие допущенные ошибки устранить нельзя, испорченные делянки исключают из опыта, в агрономическую и математическую обработку результаты не вносят.Слайд 72. Дисперсионный анализ в изложении Б.А. Доспехова
Влияние доз удобрений на
урожайность яровой пшеницы
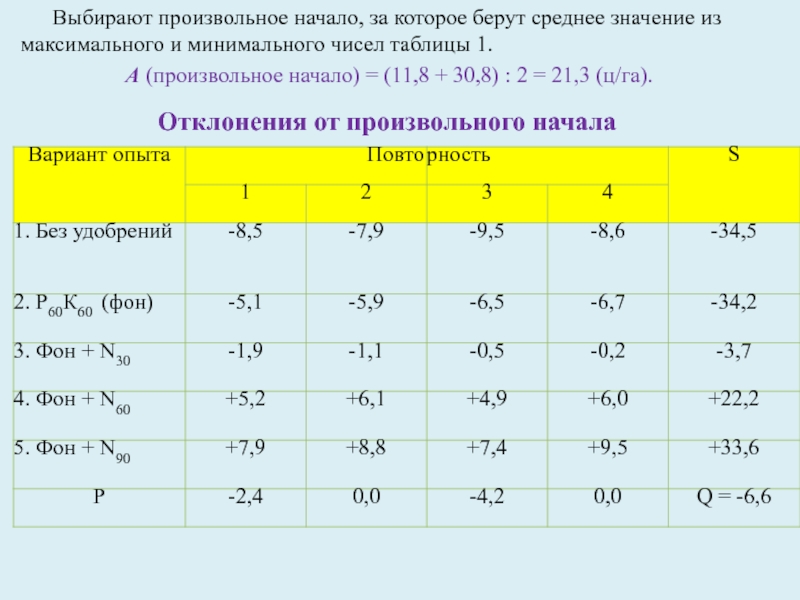
Слайд 8Выбирают произвольное начало, за которое берут среднее значение из максимального
и минимального чисел таблицы 1.
А (произвольное начало) = (11,8 +
30,8) : 2 = 21,3 (ц/га).Отклонения от произвольного начала
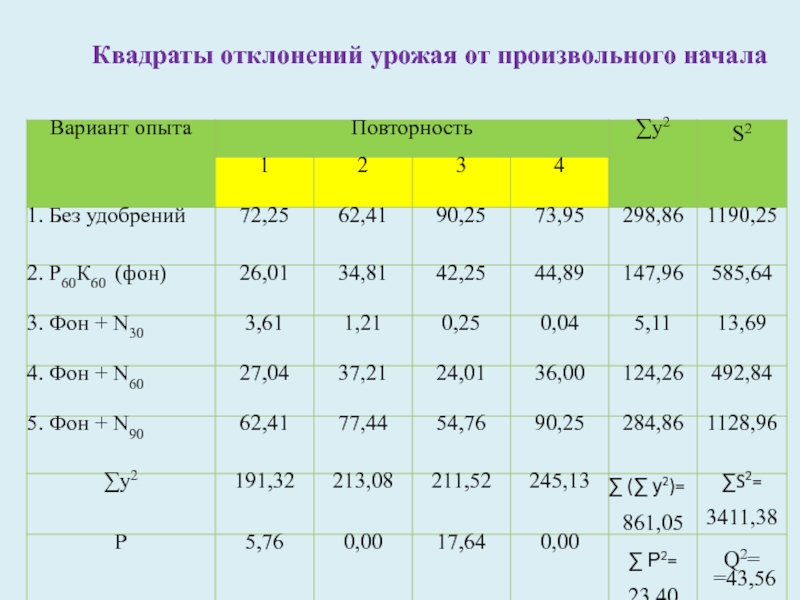
Слайд 11Далее определяют:
сумму квадратов общего рассеяния по формуле
[n*l* ∑
(∑ у2) - Q2 ] / nl
(20*861,05-43,56)/ 20=858,87
сумму квадратов рассеяния повторений[n*∑ Р2 - Q2 ] / nl
(4*23,40-43,56)/20 =2,50
сумму квадратов рассеяния вариантов
[l*∑S2- Q2 ]/ nl
(5*3411,38-43,56)/ 20=850,66
Слайд 12При проведении статистической обработки методом анализа рассеяния вводят статистический показатель
- число степеней свободы, обозначаемый буквой (Y).
Разделив сумму квадратов отклонений
на число степеней свободы, получают средний квадрат, или дисперсию.Общее число степеней свободы по остатку
YC)Cm, =nl - 1 = 4 • 5 - 1 = 19;
для рассеяния повторений Yn = n - 1 = 3;
для рассеяния вариантов Yl = l - 1 = 5 - 1 = 4.
Слайд 13Остаточное рассеяние (Cz) получают путем вычитания из общего двух последующих,
т.е. рассеяния повторений и вариантов (858,87 - 2,50 - 850,66
= 5,71).Степень свободы остаточного рассеяния определяют также путем вычитания из степени свободы общего рассеяния двух последующих (19 - 3 - 4 = 12).
Далее находят средний квадрат для вариантов, он равен 850,66 : 4 = 212,66, а для остатка 5,71 : 12 = 0,47.
Слайд 15Для установления достоверности действия изучаемых в опыте факторов в целом
по опыту находят критерий существенности Фишера (F). Различают F фактический
и F теоретический (табличный).Критерий F теоретический равен отношению среднего квадратического отклонения вариантов Gy к среднему квадратическому отклонению остатка Gz .
В нашем примере F факт= Qу2 / Qz2 = 212,66 : 0,47 = 452,46.
Критерий F факт сравнивают с F таб, если F факт больше F таб, то различия между вариантами опыта будут существенными, тогда следует находить достоверность различий между отдельными вариантами, сравниваемыми между собой. Если F факт меньше F таб, опыт проведен с большими погрешностями, дальнейшая обработка результатов опыта положительных результатов не даст.
Слайд 16 F таб находят в таблицах Фишера на пересечении
числа степеней свободы большого квадрата (вариантов, по диагонали) и меньшего
квадрата (остатка, по вертикали).Для нашего примера F таб = 3,26, т.е. он намного меньше F фактического, поэтому вычисления основных статистических показателей следует проводить.
Слайд 17Для определения относительной ошибки (точности опыта) и наименьшей существенной разницы
для установления достоверности вариантов проводят следующие вычисления:
Для оценки существенности разности
между отдельными вариантами вычисляют наименьшей существенной разности (НСР), для чего необходимо определить ошибку разности средних (Sх): (Sх) = √ S2/n
(Sх) = √ 0.47/4=0.34
и ошибку средней обобщенную (Sα):
(Sх) = √2 S2/n
(Sх) = √2 0.47/4=0.48
Слайд 18Подставляя значение Sα в формулу НСР
НСР 0,5 = t
0,5 *Sα = 2.18*0.48=1.05=1 ц/га
Теоретическое значение находят по таблице
Ошибка
средней , выраженная в % к среднему урожаю опыта , характеризует относительную точность опыта Р% = Sх*100 /Х=0,34*100/ 20,9=1,63
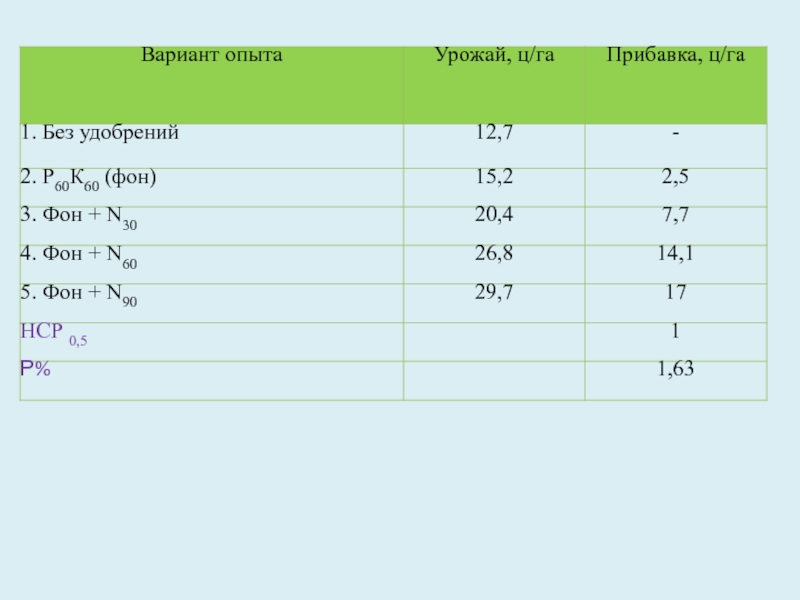
Слайд 20Величина НСР 0,5 используется при сравнении вариантов с контролем или
вариантов между собой.
Если величина прибавки урожая (ц/га) равна или
превышает величину НСР , то влияние изучаемого фактора достоверное , существенное. В нашем достоверную прибавку дает вариант 2
Слайд 213 Корреляция и регрессия в агрохимических исследованиях
Дисперсионный анализ данных урожайности
позволяет определить точность опыта и достоверность (доказуемость) испытуемых вариантов. Не
менее важной задачей в исследованиях является установление взаимосвязи урожайности с факторами, влиявшими на нее.Множественной корреляцией называют такую, когда исследуют связь урожайности с несколькими факторами, напр., с содержанием азота, фосфора, калия и других элементов в почве.
по форме корреляционная связь может быть прямолинейной и криволинейной,
по направлению - прямой и обратной.
Слайд 22Под прямолинейной корреляцией понимают такую зависимость, когда с увеличением средней
величины результативного признака (урожайности) увеличивается средняя величина другого (содержание азота
в почве) или, наоборот, с увеличением одного признака уменьшается средняя величина другого. В первом случае величина называется прямой или положительной, во втором - обратной или отрицательной.При определении тесноты связи в агрохимических исследованиях результативный признак (урожайность) принимают за Y (функция), а признаки, с которыми устанавливают связь, обозначают индексом Х (аргумент). Связь между функцией и аргументом выражают уравнением регрессии, или корреляционным уравнением. При простой регрессии уравнение имеет вид Y = f(x), а при множественной Y = f(x,z,v).
Для оценки тесноты связи вычисляют коэффициент корреляции и корреляционное отношение.
При высокой тесноте связи рассчитывают уравнение регрессии, по которому можно предсказать значение результативного признака (урожайности) в зависимости от факториальных признаков.
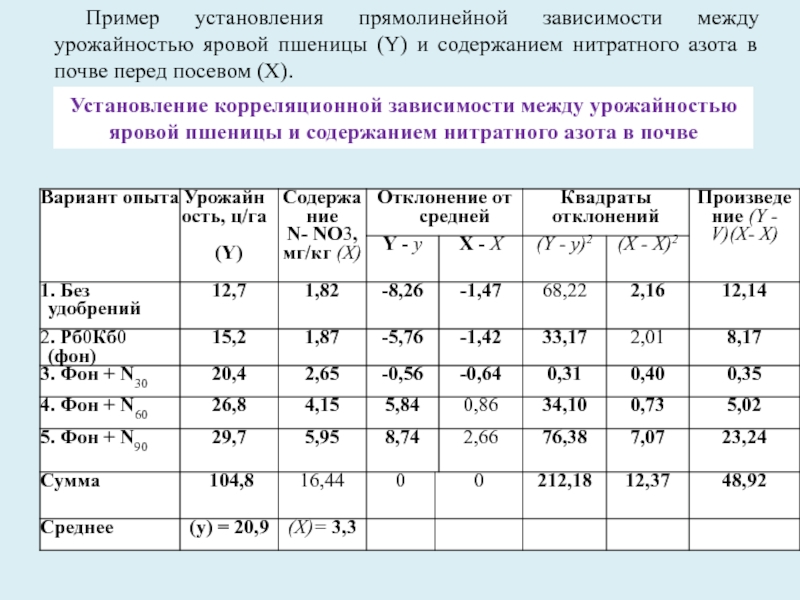
Слайд 23Пример установления прямолинейной зависимости между урожайностью яровой пшеницы (Y) и
содержанием нитратного азота в почве перед посевом (X).
Установление корреляционной зависимости
между урожайностью яровой пшеницы и содержанием нитратного азота в почвеСлайд 24 Коэффициент корреляции является безмерной величиной, изменяющейся в
интервале -1 < r < + 1. Считается, что при
г< 0,3 корреляционная зависимость между признаками (функцией и аргументом) слабая, при г = 0,3-0,7 - средняя, а при г> 0,7 - сильная.Слайд 25В нашем примере связь между урожайностью яровой пшеницы и содержанием
нитратного азота сильная.
Для оценки надежности выборочного коэффициента корреляции вычисляют его
ошибку и критерий существенности.Стандартную ошибку коэффициента корреляции определяют по формуле
где r - коэффициент корреляции;
n - число выборки, т.е. пар значений (5).
Критерий существенности коэффициента корреляции рассчитывают по формуле
г 0,95
tr = 5r = 0Д7 =5,9.
Если tr факт. > trтеор. , то корреляционная связь существенна, и наоборот, tr факт.<гтеор. - несущественна.
Теоретическое значение критерия t находят по таблице Стьюдента, принимая 5%- ный уровень значимости (приложение 3). Число степеней свободы принимают равными - 2 = 3.
В нашем примере ^еор. = 3,18, т.е. меньше, чем tr факт., следовательно, связь существенна.
Не менее важным показателем при корреляционном анализе является коэффициент детерминации (dyx), который получают возведением в квадрат коэффициента корреляции (r2). Он показывает долю в процентах тех изменений, которые зависят от изучаемого фактора. В нашем примере коэффициент детерминации dyx = 90%. Урожайность яровой пшеницы на 90% зависела от содержания азота в почве и на 10% - от других факторов.
Коэффициент корреляции указывает на тесноту связи между изучаемыми признаками, но не позволяет судить, как изменяется функция (Y) при изменении аргумента на единицу измерения. Это можно решить с помощью регрессионного анализа.
Уравнение линейной регрессии Y на Х имеет вид Y = y-byx(X-X), где X и у - средние арифметические для ряда Х и Y; byx - коэффициент регрессии Y по Х.
Коэффициенты регрессии вычисляют по формулам:
byx = = = 3,95;
bxy = = = 0,23.
Произведение коэффициентов регрессии равняется квадрату коэффициента корреляции: byxbxy = r2 = 3,95 • 0,23 = 0,9.
Подставив найденные значения в уравнение линейной регрессии, вычисляют уравнение прямой линии Y = 20,9 + 3,95 (Х - 3,29) = 7,96+ 3,95Х.
По уравнению линейной регрессии корреляционная связь может быть изображена графически. Построив график уравнения простой линейной корреляции и имея цифровые показатели аргумента (Х), можно рассчитать ожидаемую урожайность культуры.
Слайд 26Какие ошибки сопровождают полевой опыт и как они влияют на
точность опыта и достоверность результатов?
Что позволяет определить дисперсионный анализ?
Какие основные
статистические характеристики получают в дисперсионном анализе?Напишите последовательность расчетов в дисперсионном анализе по Б.А. Доспехову.
Что такое корреляция и регрессия?
Какие вопросы решаются с их помощью?
Как определить простую прямолинейную корреляционную связь?
Что такое индекс детерминации и как он определяется?
Слайд 27Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман.
- М.: Высшая школа, 2003. - 523 с.
Дмитриев, Е.А. Математическая
статистика в почвоведении / Е.А. Дмитриев. -М.: Книжный дом «ЛИБРОКОМ», 2009. - 328 с.Кремер, Н.Ш. Теория вероятности и математическая статистика / Н.Ш. Кремер. - М.: Юнити- Дана, 2002. - 343 с.
Пискунов, А.С. Методы агрохимических исследований / А.С. Пискунов. - М.: КолосС, 2004. - 312 с.







![Лекция № 8-9 Дисперсионный анализ результатов опыта Далее определяют:сумму квадратов общего рассеяния по формуле [n*l* ∑ (∑ у2) Далее определяют:сумму квадратов общего рассеяния по формуле [n*l* ∑ (∑ у2) - Q2 ] / nl](/img/thumbs/35220b54394f4fc86b81a7c34d647c54-800x.jpg)