Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
лекция №3 Дополнительные проекции
Содержание
- 1. лекция №3 Дополнительные проекции
- 2. Дополнительные ортогональные проекции
- 3. Этот метод опирается на основные положения ортогонального
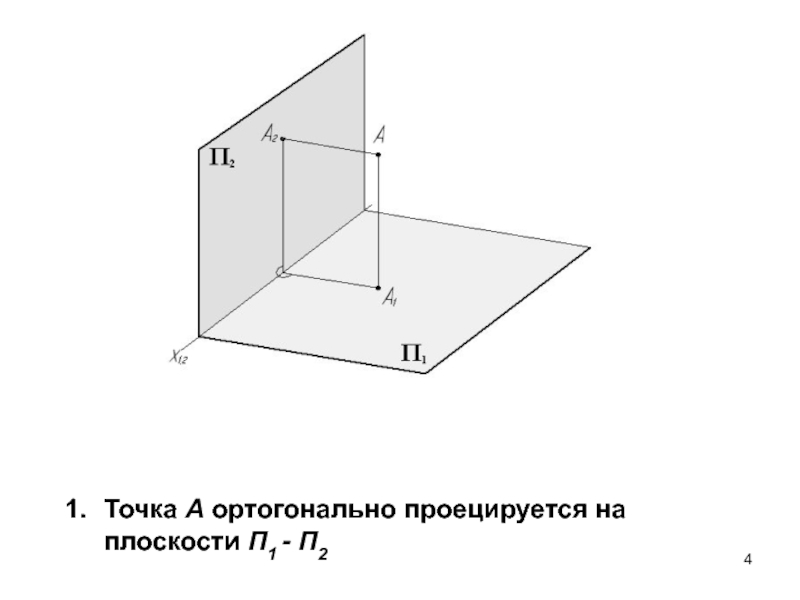
- 4. Точка A ортогонально проецируется на плоскости П1 - П2
- 5. 2. Вместо плоскости П2 вводим плоскость П4
- 6. 4. Ортогональные проекции точки A в новой
- 7. 5. Плоскость П4 поворачивается вокруг оси x14
- 8. Проводим ось x14 , обозначая новую систему
- 9. Дополнительная проекции прямой на плоскость ей параллельную(П4
- 10. Проекция прямой на плоскость ей перпендикулярную2. (П5
- 11. Выполняем:1. - проводим ось x14, обозначая новую
- 12. Преобразование линии уровня h в проецирующую прямуюНовая плоскость П4 перпендикулярна прямой AB и плоскости П1
- 13. Метрические задачи 1. Определение расстояния
- 14. Проекция плоскости на плоскость ей перпендикулярную1. В
- 15. Метрические задачи2. Определение расстояния от точки до
- 16. Проекция плоскости на плоскость ей параллельнуюП4 (АВС), П4П1П4h 2) П5 II (АВС), П5 П4
- 17. П4 (АВС), П4П1П4h 2) П5 II
- 18. Метрические задачи3. Определение натуральной величины ула между
- 19. Необходимо построить ортогональную проекцию двугранного угла на
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Этот метод опирается на основные положения ортогонального проецирования
Новая плоскость проекций
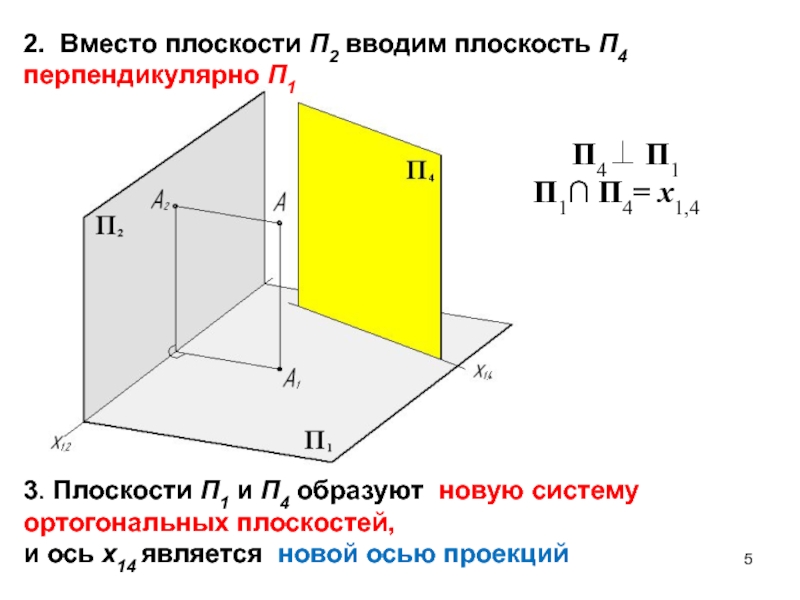
Слайд 52. Вместо плоскости П2 вводим плоскость П4 перпендикулярно П1
П4 П1
П1∩ П4= х1,4
3. Плоскости П1 и П4 образуют
новую систему ортогональных плоскостей, и ось x14 является новой осью проекций
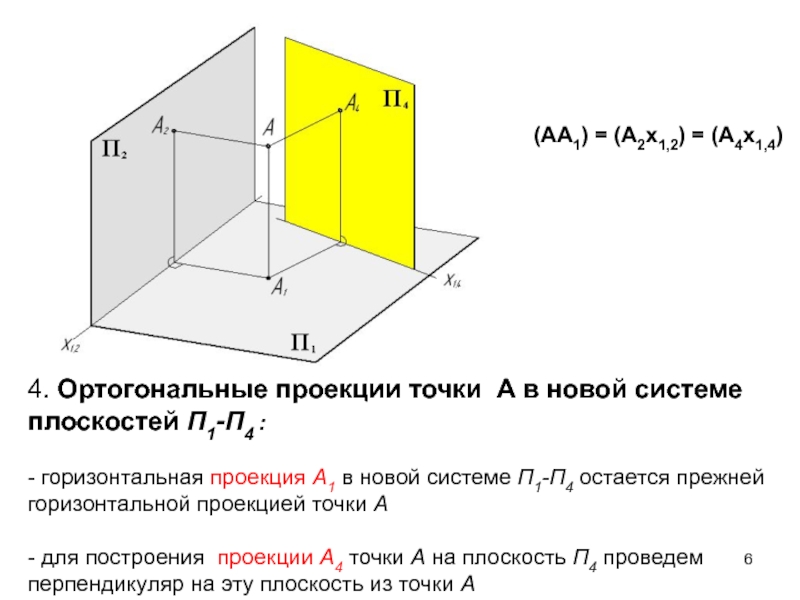
Слайд 64. Ортогональные проекции точки A в новой системе плоскостей П1-П4
:
- горизонтальная проекция A1 в новой системе П1-П4 остается прежней
горизонтальной проекцией точки A- для построения проекции A4 точки A на плоскость П4 проведем перпендикуляр на эту плоскость из точки A
(АА1) = (А2х1,2) = (А4х1,4)
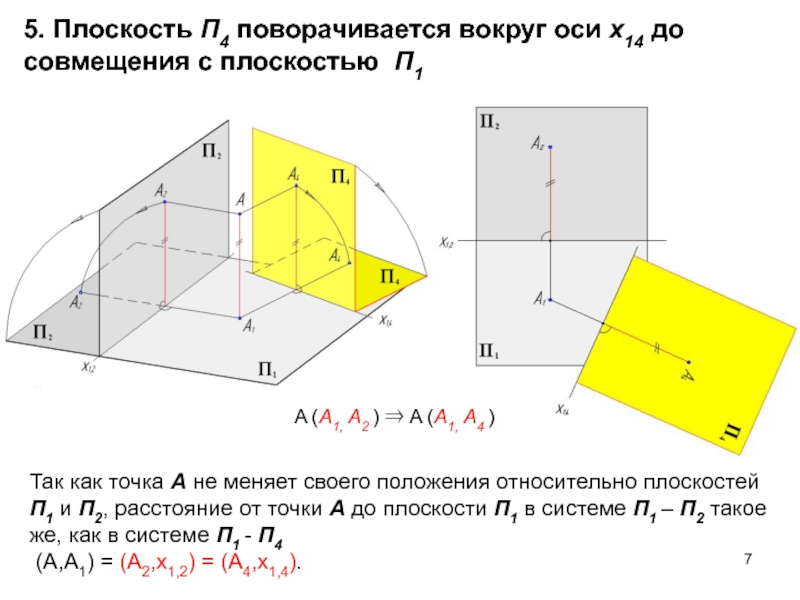
Слайд 75. Плоскость П4 поворачивается вокруг оси x14 до совмещения с
плоскостью П1
Так как точка A не меняет своего положения относительно
плоскостей П1 и П2, расстояние от точки A до плоскости П1 в системе П1 – П2 такое же, как в системе П1 - П4 (А,А1) = (А2,х1,2) = (А4,х1,4).
A (A1, A2 ) A (A1, A4 )
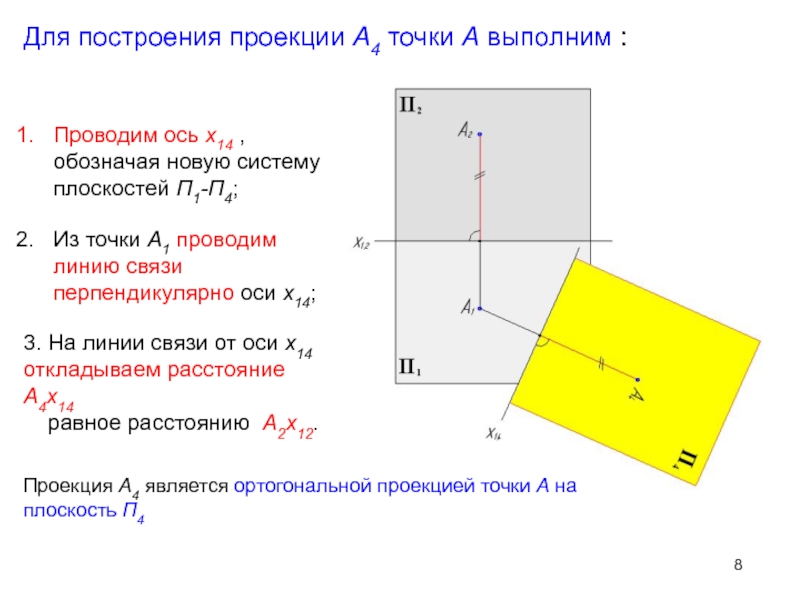
Слайд 8Проводим ось x14 , обозначая новую систему плоскостей П1-П4;
Из точки
A1 проводим линию связи перпендикулярно оси x14;
3. На линии связи
от оси x14 откладываем расстояние A4x14равное расстоянию A2x12.
Для построения проекции A4 точки A выполним :
Проекция A4 является ортогональной проекцией точки A на плоскость П4
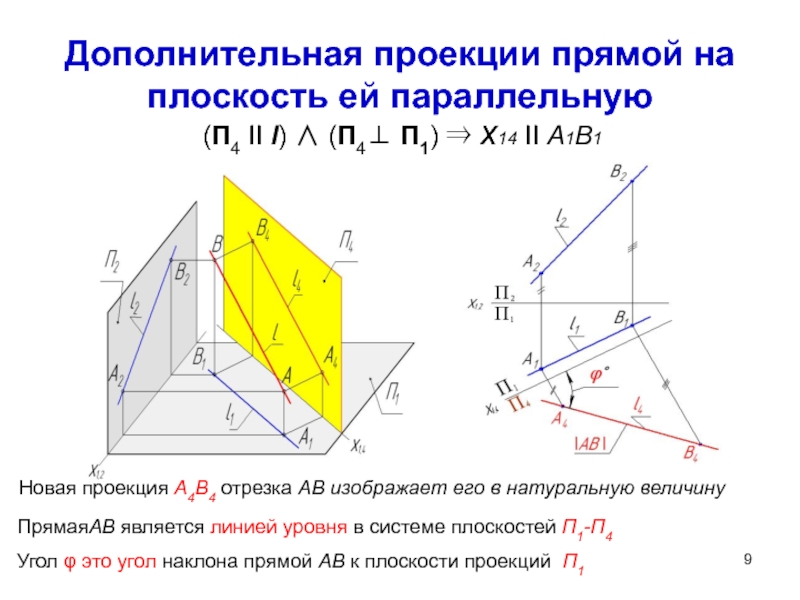
Слайд 9Дополнительная проекции прямой на плоскость ей параллельную
(П4 II l)
(П4 П1) x14 II A1B1
ПрямаяAB является линией уровня в
системе плоскостей П1-П4Новая проекция A4B4 отрезка AB изображает его в натуральную величину
Угол φ это угол наклона прямой AB к плоскости проекций П1
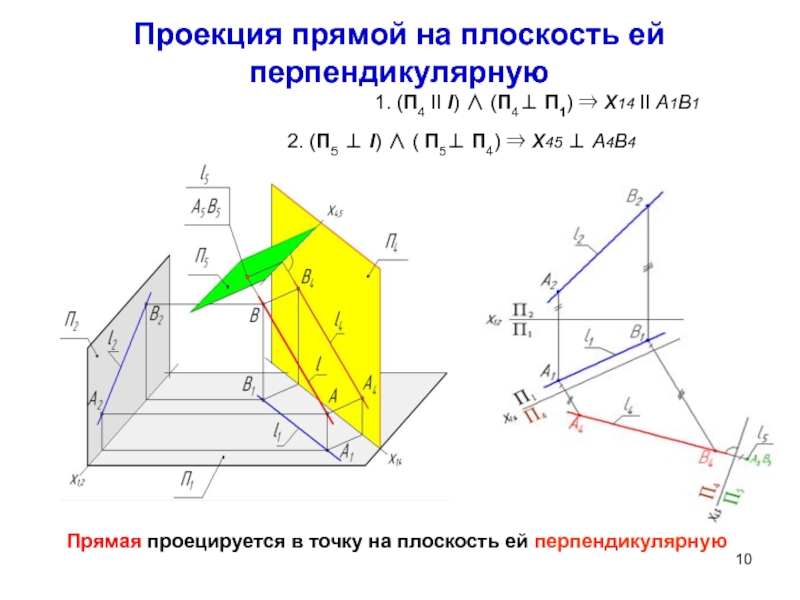
Слайд 10Проекция прямой на плоскость ей перпендикулярную
2. (П5 l)
( П5 П4) x45 A4B4
1. (П4 II l)
(П4 П1) x14 II A1B1 Прямая проецируется в точку на плоскость ей перпендикулярную
Слайд 11Выполняем:
1. - проводим ось x14, обозначая новую систему плоскостей П1-П4;
2.
– строим проекцию A4B4 – проекцию отрезка AB на плоскость
П4;3. – проводим осьx45 , задавая следующую систему плоскостей проекций П4-П5 перпендикулярно проекции A4B4;
4. – от оси x45 откладываем расстояние равное расстоянию от точек A1 и B1 до оси x14;
5. - отмечаем A5=B5 , что является проекцией AB на плоскость П5.
1. - проводим ось x14, обозначая новую систему плоскостей П1-П4;
2. – строим проекцию A4B4 – проекцию отрезка AB на плоскость П4;
3. – проводим осьx45 , задавая следующую систему плоскостей проекций П4-П5 перпендикулярно проекции A4B4;
4. – от оси x45 откладываем расстояние равное расстоянию от точек A1 и B1 до оси x14;
5. - отмечаем A5=B5 , что является проекцией AB на плоскость П5.
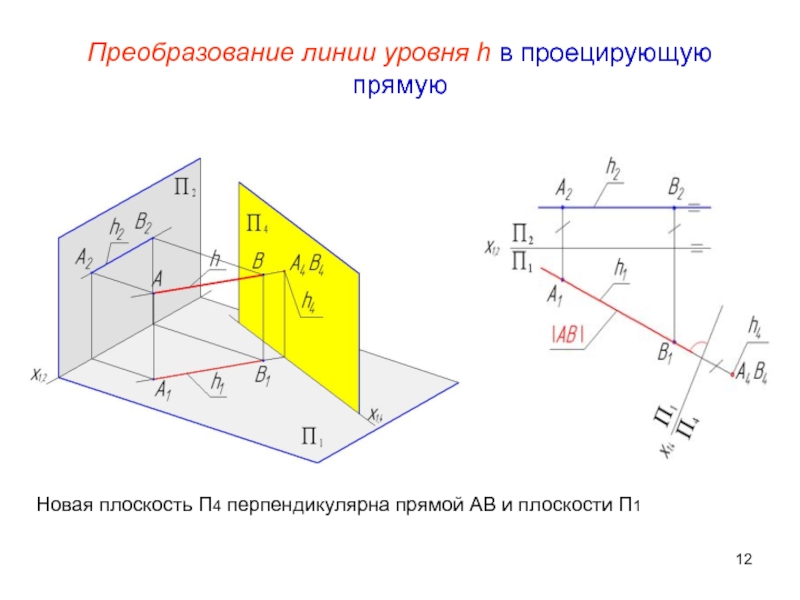
Слайд 12Преобразование линии уровня h в проецирующую прямую
Новая плоскость П4 перпендикулярна
прямой AB и плоскости П1
Слайд 13
Метрические задачи
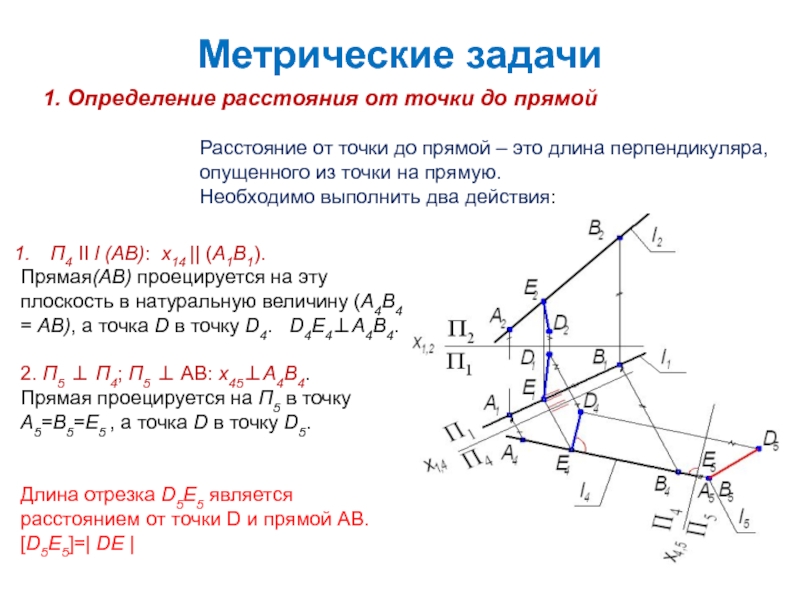
1. Определение расстояния от точки до прямой
Расстояние от
точки до прямой – это длина перпендикуляра, опущенного из точки
на прямую.Необходимо выполнить два действия:
П4 II l (AB): x14 || (A1B1).
Прямая(AB) проецируется на эту плоскость в натуральную величину (A4B4 = AB), а точка D в точку D4. D4E4A4B4.
2. П5 П4; П5 AB: x45A4B4.
Прямая проецируется на П5 в точку A5=B5=E5 , а точка D в точку D5.
Длина отрезка D5E5 является расстоянием от точки D и прямой AB.
[D5E5]=| DE |
Слайд 14Проекция плоскости на плоскость ей перпендикулярную
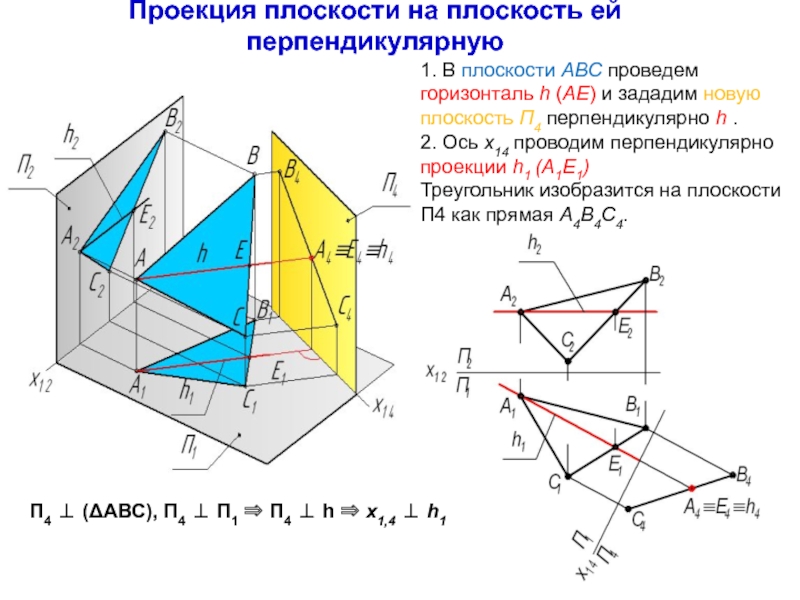
1. В плоскости ABC проведем
горизонталь h (AE) и зададим новую плоскость П4 перпендикулярно h
.2. Ось x14 проводим перпендикулярно проекции h1 (A1E1)
Треугольник изобразится на плоскости П4 как прямая A4B4C4.
П4 (АВС), П4 П1 П4 h х1,4 h1
Слайд 15Метрические задачи
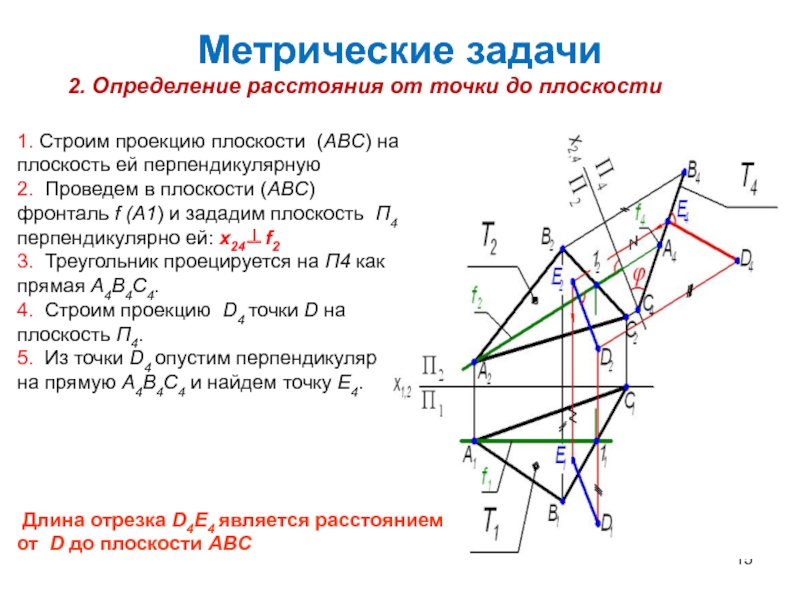
2. Определение расстояния от точки до плоскости
1. Строим проекцию
плоскости (ABC) на плоскость ей перпендикулярную
2. Проведем в плоскости (ABC)
фронталь f (A1) и зададим плоскость П4 перпендикулярно ей: x24f2 3. Треугольник проецируется на П4 как прямая A4B4C4.
4. Строим проекцию D4 точки D на плоскость П4.
5. Из точки D4 опустим перпендикуляр на прямую A4B4C4 и найдем точку E4.
Длина отрезка D4E4 является расстоянием от D до плоскости ABC
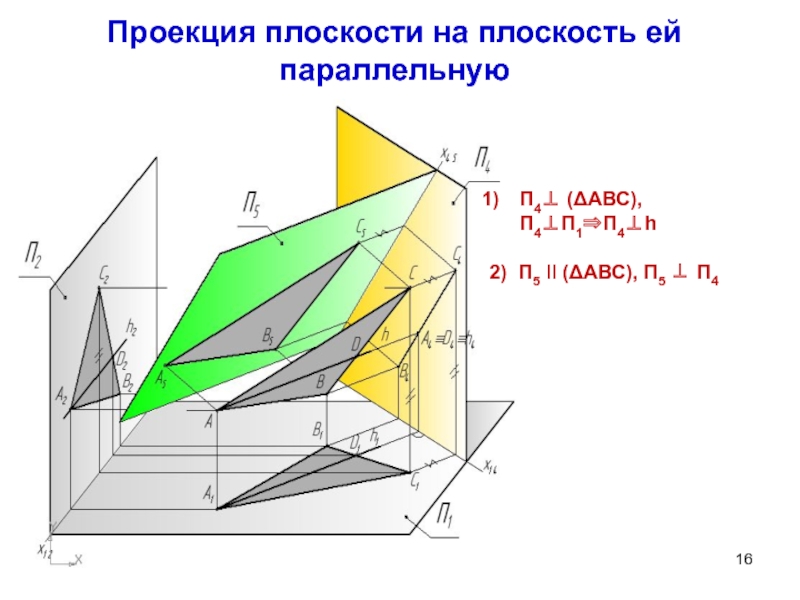
Слайд 16Проекция плоскости на плоскость ей параллельную
П4 (АВС), П4П1П4h
2) П5 II
(АВС), П5 П4
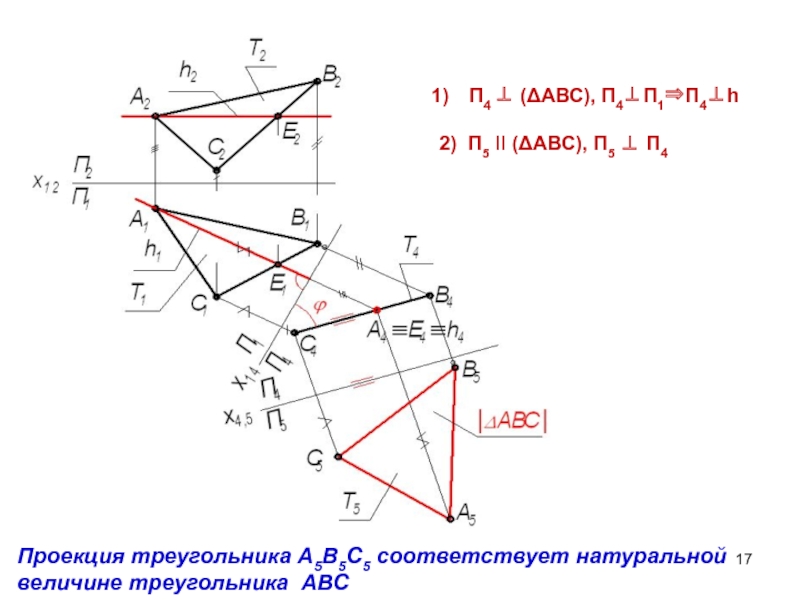
Слайд 17П4 (АВС), П4П1П4h
2) П5 II (АВС), П5 П4
Проекция
треугольника A5B5C5 соответствует натуральной величине треугольника ABC
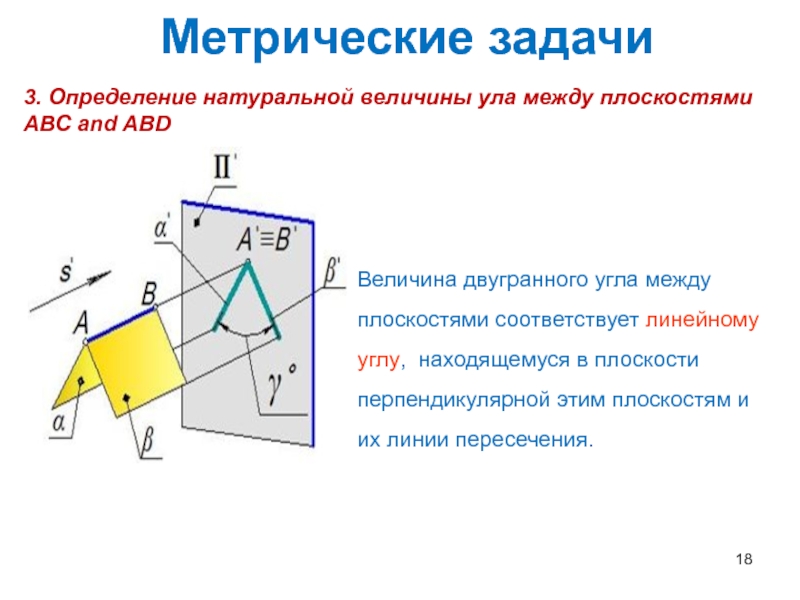
Слайд 18Метрические задачи
3. Определение натуральной величины ула между плоскостями ABC and
ABD
Величина двугранного угла между плоскостями соответствует линейному углу, находящемуся в
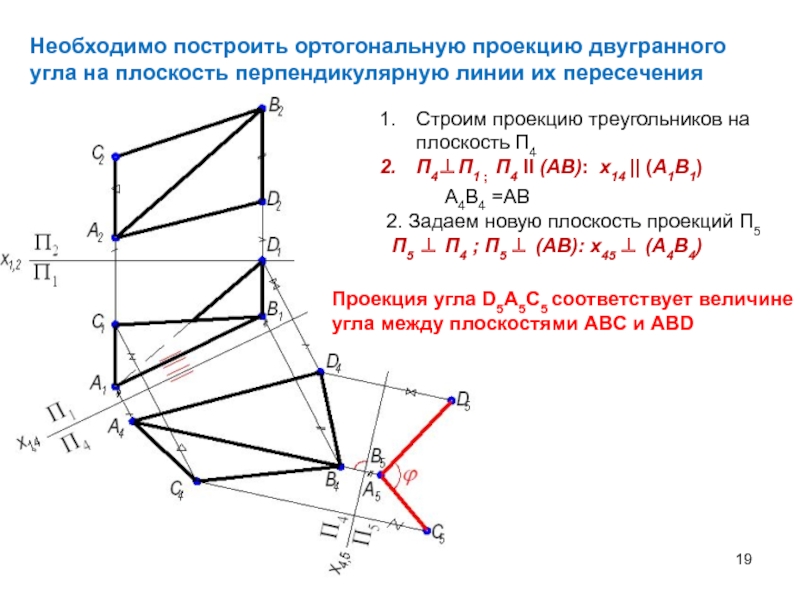
плоскости перпендикулярной этим плоскостям и их линии пересечения.Слайд 19Необходимо построить ортогональную проекцию двугранного угла на плоскость перпендикулярную линии
их пересечения
Строим проекцию треугольников на плоскость П4
П4П1 ; П4
II (AB): x14 || (A1B1)A4B4 =AB
2. Задаем новую плоскость проекций П5
П5 П4 ; П5 (AB): x45 (A4B4)
Проекция угла D5A5C5 соответствует величине угла между плоскостями ABC и ABD