Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация-Непрерывные коды-Сизых СД.ppt
Содержание
- 1. Презентация-Непрерывные коды-Сизых СД.ppt
- 2. Тема презентации:Непрерывные коды
- 3. Работу выполнил:Сизых С. Д.Студент группы П-31Факультета ИВТ, 3-й курса
- 4. ОглавлениеКлассификация кодовПомехоустойчивые коды Блочные коды
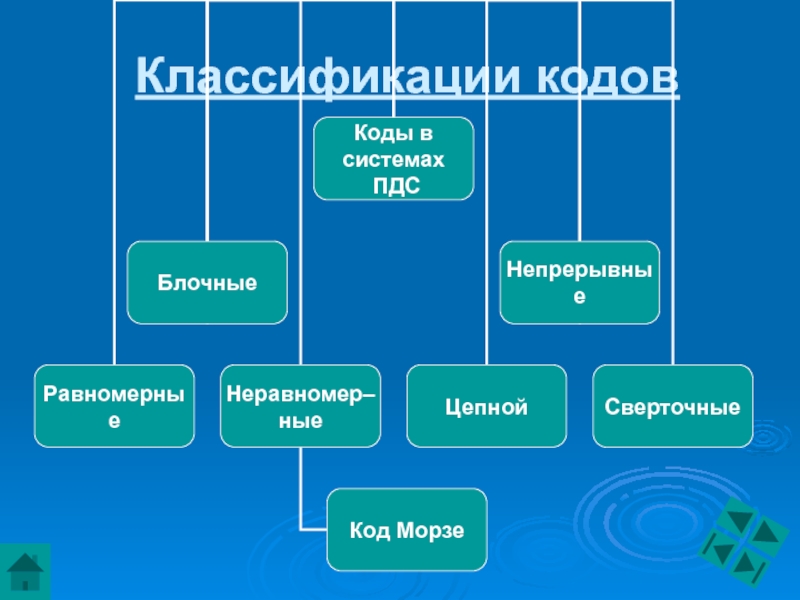
- 5. Классификации кодов
- 6. Классификация кодов
- 7. Помехоустойчивые коды Помехоустойчивые коды делятся
- 8. Блочные коды В связи с этим
- 9. Понятие о непрерывных кодах Непрерывные
- 10. Блочные коды Разновидностями как блочных, так
- 11. Понятие о непрерывных кодах В непрерывных
- 12. Понятие о непрерывных кодах Эти коды
- 13. Цепной код В данном коде после
- 14. Цепной код Из информационных элементов (а0,
- 15. Цепной кодна приеме выделяются отдельно информационныеэлементы и
- 16. Цепной код При отсутствии ошибок принятые
- 17. Цепной код Рассмотренный цепной код за
- 18. Сверточные коды Рассмотренный цепной код является
- 19. Сверточные коды Если передача информации происходит
- 20. Сверточные коды Выходные проверочные последовательности можнопредставить
- 21. Сверточные коды Полиномы G(j)(x),…, Z(j)(x), называются
- 22. Сверточные коды Для пояснения
- 23. Сверточные коды Таким образом, кодирование заключается
- 24. Сверточные коды Если на вход кодирующего
- 25. Сверточные коды Из (7.22) видно, что
- 26. Сверточные коды При декодировании принятые последовательностиинформационных
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 7Помехоустойчивые коды
Помехоустойчивые коды делятся на:
Блочные
Непрерывные
К блочным относятся коды, в которых каждому сообщению
отводится блок из
n символов (разрядов) или блоки с разным числом символов.
Слайд 8Блочные коды
В связи с этим блочные коды делятся
на:
равномерные,
неравномерные.
Широкое практическое применение нашли равномерные коды.
К неравномерным кодам
относятся, например, код Морзе.
Слайд 9Понятие о непрерывных кодах
Непрерывные коды, к
которым относятся
рекуррентные (сверточные),
цепной,
представляют собой непрерывные
последовательностит единичных элементов, не
разделенные на блоки.
Слайд 10Блочные коды
Разновидностями как блочных, так и
непрерывных кодов являются:
разделимые
(с возможностью выделения информационных и контрольных символов)
неразделимые коды.
Слайд 11Понятие о непрерывных кодах
В непрерывных кодах избыточные разряды
помещаются в
определенном порядке между информационными разрядами.
Непрерывные коды характеризуются тем, что
первичнаяпоследовательность символов, несущих информацию,
непрерывно преобразуется по определенному закону в
другую последовательность, содержащую избыточное число
символов. В непрерывных кодах операции кодирования
и декодирования производятся непрерывно над
последовательностью информационных символов без
деления ее на блоки. К таким кодам относятся цепной и
сверточные.
Слайд 12Понятие о непрерывных кодах
Эти коды применяются для обнаружения
и исправления пачек
ошибок. Для сверточных кодов разработаны специальные
процедуры последовательного декодирования,
позволяющиеупростить их техническую реализацию.
Слайд 13Цепной код
В данном коде после каждого информационного элемента
следует
проверочный элемент. Проверочные элементы
формируются путем сложения по модулю 2 двух
информационных
элементов, отстоящих друг от друга на шагсложения l. Шаг l — это расстояние между двумя
информационными элементами, формирующими
проверочный элемент.
Обозначим через а0 , а1 ..., аl, аl+1 ...,a2l+1 ... информацион-
ную последовательность, элементы которой отстоят друг от
друга на шаг сложения l. В отличие от обозначений
предыдущих разделов проверочные разряды будем
обозначать через b.
Слайд 14Цепной код
Из информационных элементов (а0, аl), (а1, аl+1),
…
формируются следующие проверочные элементы по правилу
b0,l= a0+al;
b1,l+1=a0+al+1,…
bl+1,2l+1=al+1+a2l+1
(7.18)
Закодированная цепным кодом последовательность будет
иметь вид
a0b0la1b1,l+1a2b2,l+2,… ,al+1bl+1,2l+1.
Избыточность такого кода, очевидно, равна 0,5. Процесс
декодирования принимаемой кодовой последовательности
определяется принципом формирования проверочных
элементов и заключается в следующем:
Слайд 15Цепной код
на приеме выделяются отдельно информационные
элементы и отдельно проверочные элементы;
из принятой последовательности информационных
разрядов по известному правилу кодирования (7.18)
формируются новые
проверочные разряды; каждый сформированный проверочный разряд
сравнивается по модулю 2 с принятым проверочным
элементом.
Слайд 16Цепной код
При отсутствии ошибок принятые и вычисленные
проверочные разряды,
очевидно, совпадают. Наличие
ошибок приведет к несовпадению этих разрядов. (Указанная
процедура эквивалентна
нахождению синдрома в кодеХемминга.)
Корректирующие возможности цепного кода
зависят от шага сложения l. Изменяя его, можно построить
код, обнаруживающий и исправляющий пачки ошибок длиной
tи.ош.=2l [7.1]. Показано, что при шаге сложения l код
исправляет пачки ошибок длиной t, если каждый
проверочный элемент перед передачей в канал связи
задерживается на время t*τ0 с и рядом расположенные пачки
ошибок разделены между собой защитным интервалом Т, не
содержащим ошибок. При этом T=6*l+1, t=(3*l+1)*τ0 то, где τ0
— длительность единичного элемента.
Слайд 17Цепной код
Рассмотренный цепной код за счет большой избыточности
сравнительно
просто позволяет обнаруживать или
исправлять пачки ошибок. Изменяя шаг сложения, можно
согласовывать
корректирующие способности кода схарактеристиками ошибок в канале связи.
Слайд 18Сверточные коды
Рассмотренный цепной код является простейшим случаем
сверточных
кодов. В основу сверточного кодирования
положен принцип формирования последовательности
проверочных элементов линейной
комбинацией элементовинформационной последовательности, поступающей
непрерывно на вход кодирующего устройства. Сверточные
коды могут иметь произвольную скорость k/n. Кодер
сверточного кода имеет к входов и n выходов. Эти коды
могут быть разделимыми и неразделимыми. В последнем
случае в каждый дискретный момент времени на входы
кодирующего устройства поступают к информационных
символов, а с выходов считываются n символов, из которых
к символов являются информационными, а остальные n—к
линейными комбинациями информационных
последовательностей и образуют последовательность
проверочных элементов.
Слайд 19Сверточные коды
Если передача информации происходит по одному
каналу,
но к выходу кодирующего устройства подключается
специальная коммутирующая схема.
Представим
входные информационные о следовательностив виде к полиномов:
A(1)(x)=a0(1)+ a1(1)*x+…+ ai(1)*x(i)+…,
A(2)(x)=a0(2)+ a1(2)*x+…+ ai(2)*x(i)+…,
………………………………………,
A(k)(x)=a0(k)+ a1(k)*x+…+ ai(k)*x(i)
Слайд 20Сверточные коды
Выходные проверочные последовательности можно
представить в виде
n—k полиномов:
B(1)(x)=b0(1)+ b1(1)*x+…
B(2)(x)=b0(2)+ b1(2)*x+…
B(n-k)(x)=b0(n-k)+ b1(n-k)*x+…
Поскольку в сверточном коде
проверочныепоследовательности являются линейными комбинациями
информационных последовательностей, то согласно алгебре
многочленов проверочная последовательность может быть
записана в виде
B(j)(x)=A(1)(x)G(j)(x)+ A(2)(x)H(j)(x)+…+A(k)(x)Z(j)(x), (7.19)
где j=1, 2, ... n—к.
Слайд 21Сверточные коды
Полиномы G(j)(x),…, Z(j)(x), называются образующими (по
терминологии
циклических кодов). Если r — наибольшая
степень образующих полиномов, то любой
информационныйэлемент будет оказывать влияние на проверочную
последовательность B(j)(x) на протяжение не более r+1
тактов. В течение этого времени с выхода кодирующего
устройства будет считано m=n(r+1) символов. Величину т
называют кодовым ограничением сверточного кода. Для
сверточных кодов со скоростью передачи k/n число
образующих полиномов равно k(n—k). Начальным кодовым
словом сверточного кода называют первую совокупность
символов на выходах кодирующего устройства.
Слайд 22Сверточные коды
Для пояснения принципа кодирования
рассмотрим случай,
когда скорость кода равна k/n=1/2. Тогда число образующих
полиномов равно
k(n—k)=l. Возьмем образующий полиномстепени r:
G(x)=g0+g1*x+…+ gr*xr, gi=0,1.
При поступлении на вход кодера информационной
последовательности а0,а1,а2 на выходе получаем
информационную последовательность а0,а1,а2,
совпадающую с исходной, и проверочную
последовательность b0,b1,b2. Представляя эти
последовательности в виде полиномов и используя (7.19),
имеем
B(x)=G(x)A(x). (7.20)
Слайд 23Сверточные коды
Таким образом, кодирование заключается в вычислении
произведения
В(х). С учетом того, что операция умножения
происходит в поле GF(2),
вычисление В(х) осуществляетсялинейным много-тактным фильтром, содержащим регистры и
сумматор по модулю 2 (но без обратных связей). Значения
проверочных элементов определяются выражением
bi=g0*аi +g1*ai-1 +g2*аi-2 +…+gr*аi-r (7.21)
Слайд 24Сверточные коды
Если на вход кодирующего устройства информационные
символы
поступают поочередно, то проверочные разряды bi
в соответствии с (7.20) будут
формироваться следующимобразом:
b0=g0*а0,
b1=g0*а1+g1*а0,
b2=g0*а2+g1*а1+g2*а0,
.
.
.
Br=g0*аr+g1*аr-1+…+gr*а0.
(7.22)
Слайд 25Сверточные коды
Из (7.22) видно, что формирование проверочных
разрядов
происходит суммированием по модулю 2 каждого
информационного разряда с некоторым набором
предыдущих
разрядов. Подобная рекуррентная процедура иобъясняет название этих кодов как непрерывных
(рекуррентных). Рассмотренный выше цепной код является
простейшим частным случаем такого кода. Очевидно, что
структура сверточного кода полностью определяется
образующим полиномом.
Слайд 26Сверточные коды
При декодировании принятые последовательности
информационных и проверочных
символов могут
вследствие ошибок отличаться от переданных.
Декодирование сверточного кода осуществляется
следующим образом.
Принятая информационнаяпоследовательность кодируется так же, как это делается на
передаче, далее выполняется сложение по модулю 2 с
принятой проверочной последовательностью. В результате
получается корректирующая последовательность, по которой
можно исправить ошибки.
Существуют различные процедуры декодирования, среди
которых наиболее эффективен алгоритм Возенкрафта-Фано
[7.1, 7.2]. Подробнее со свойствами сверточных кодов можно
ознакомиться в [7.1].