Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейные преобразования, линейный оператор
Содержание
- 1. Линейные преобразования, линейный оператор
- 2. Линейное преобразованиеОпределение 1.2 Пусть U и
- 3. Слайд 3
- 4. Замечания:(1) Говорят, что линейный оператор сохраняет операции.(2)
- 5. Пример 1.3Доказать, что следующее преобразование :R2
- 6. Пример 1.4Показать, что следующее преобразование T: R3
- 7. Пример 1.5Пусть Pn – векторное пространство действительных
- 8. Пример 1.6Обозначим через D оператор дифференцирования для
- 9. Нулевое преобразование:Единичный оператор:
- 10. Теорема 1.7: (Свойства линейного преобразования)(1) Пусть
- 11. 2.Матричное преобразование Теорема 2.1. Пусть A есть
- 12. Пример 2.2Рассмотрим матрицу
- 13. Пример 2.3. Поворот на плоскостиРассмотрим
- 14. r:длина (v)θ +α:
- 15. 3. Матрица линейного оператораПусть задано линейное преобразование
- 16. Матрица линейного оператораПусть задан линейный оператор
- 17. Матрица линейного оператораОпределение 3.1. МатрицаНазывается матрицей линейного оператора в базе В.
- 18. 4. Подобные матрицыПусть даны два базиса В
- 19. 4. Подобные матрицы (продолжение)Получим
- 20. Теорема 4.3: (Свойства подобных матриц)Пусть матрицы S и T подобны, тогдаДоказательство.
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 11. Линейные преобразования, линейный оператор
2.Матричное преобразование
3.Матрица линейного оператора
4.Подобные матрицы
Линейные преобразования,
Слайд 2Линейное преобразование
Определение 1.2
Пусть U и V - векторные пространства.
Пусть u и v - векторы из U пусть c
- скаляр. Говорят, что преобразование : U → V является линейным, если
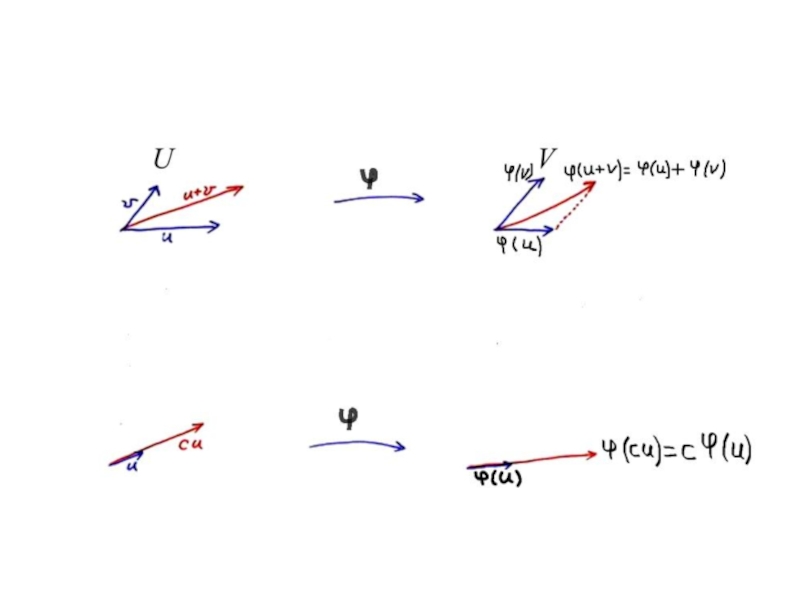
(u + v) = (u) + (v) и
(cu) = c (u).
Определение 1.1
Пусть U и V - векторные пространства.
Преобразование : U → V есть отображение, которое каждому вектору u из U ставит в соответствие уникальный вектор v из V.
Слайд 4Замечания:
(1) Говорят, что линейный оператор сохраняет операции.
(2) Линейное преобразование
векторного пространства в себя называется линейным оператором.
Слайд 5Пример 1.3
Доказать, что следующее преобразование :R2 → R2 линейно.
(x,
y) = (x − y, 3x)
“×”: Пусть c - скаляр.
(c(x1, y1)) = (cx1, c y1) = (cx1 − cx2, 3cx1)= c (x1 − y1, 3x1) = c (x1, y1)
– линейное преобразование.
Слайд 6Пример 1.4
Показать, что следующее преобразование T: R3 → R2 не
является линейным.
(x, y, z) = (xy, z)
не является
линейным преобразованием.И (x1, y1, z1) + (x2, y2, z2) = (x1y1, z1) + (x2y2, z2)
Поэтому
((x1, y1, z1) + (x2, y2, z2)) ≠ (x1, y1, z1) + (x2, y2, z2).
Слайд 7Пример 1.5
Пусть Pn – векторное пространство действительных многочленов степени ≤
n. Показать, что следующее преобразование : P2 →
P1 является линейным.(ax2 + bx + c) = (a + b)x + c
Решение
“×”: Пусть k – произвольный скаляр.
Слайд 8Пример 1.6
Обозначим через D оператор дифференцирования для действительных многочленов (D
есть то же самое, что и .)
D можно интерпретировать как отображение Pn в себя.
Например,
Пусть а c - скаляр. Следующие свойства производной показывают, что D есть линейный оператор.
D(f + g) = Df + Dg
D(cf) = cD(f)
Слайд 10Теорема 1.7: (Свойства линейного преобразования)
(1) Пусть v – произвольный
вектор из V.
(0)= (0v)
= 0 (v) = 0(2) (-v) = ((-1)v) = (-1) (v)= - (v)
(3) (u-v)= (u + (-1)v) = (u) + (-1) (v) = (u) - (v)
Доказательство.
Слайд 112.Матричное преобразование
Теорема 2.1. Пусть A есть m×n матрица. Пусть
v есть элемент пространства Fn, интерпретируемый как столбец. Преобразование
: Fn→Fm, определенное как (v)=Av, является линейным. Такое линейное преобразование называется матричным преобразованием.(линейность)
A : m×n матрица, v : n×1 матрица, Av : m×1 матрица
⇒ (x)=Ax определяет преобразование из Fn в Fm.
Пусть u, v ∈ Fn, и c ∈ F.
(u+v)=A(u+v) = Au+Av = (u) + (v )
(cv)=A(cv) = cAv = c (v)
⇒ – линейное преобразование.
Слайд 12Пример 2.2
Рассмотрим матрицу
и
столбец из R3.Эта матрица задает линейное преобразование (x)=Ax из R3 в R2, использующее матричное умножение.
Например,
и
Слайд 13Пример 2.3. Поворот на плоскости
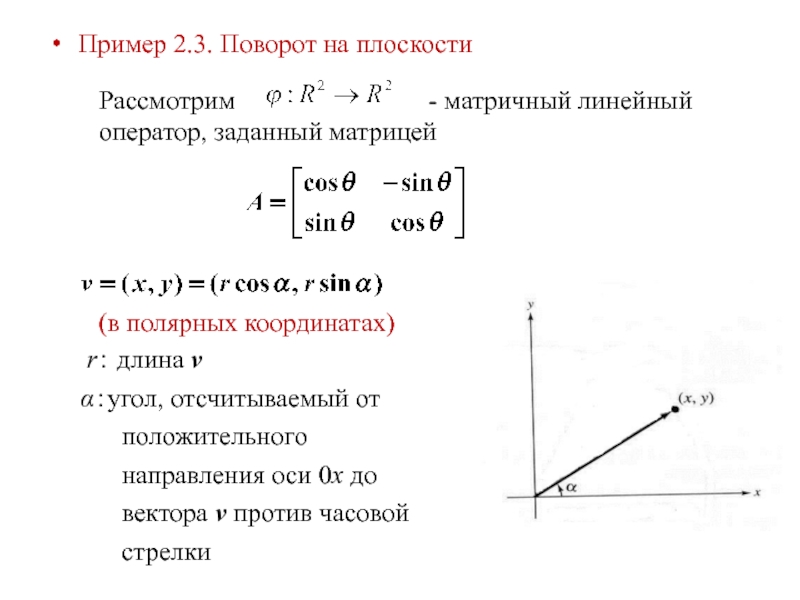
Рассмотрим
-
матричный линейный оператор, заданный матрицей(в полярных координатах)
r: длина v
α:угол, отсчитываемый от положительного направления оси 0x до вектора v против часовой стрелки
Слайд 14 r:длина (v)
θ +α: угол, отсчитываемый от
положительного направления оси 0x до вектора (v) против
часовой стрелки.Следовательно, (v) есть вектор, полученный поворотом вектора v против часовой стрелки на угол θ.
Слайд 153. Матрица линейного оператора
Пусть задано линейное преобразование :
U→V и произвольный базис {b1 , b2 , …, bn
} пространства U, тогда образ (v) произвольного вектора v из U можно вычислить из образов (b1), (b2), …, (bn)базисных векторов. Это можно сделать, выражая v как линейную комбинацию базисных векторов
v = c1 b1+ c2 b2+ …+ cn bn
и затем используя Теорему 1.7:
(v) = c1 (b1) + c2 (b2) + … + cn (bn)
Другими словами, линейное преобразование полностью определяется образами векторов из любого из базисов исходного векторного пространства.
Слайд 16Матрица линейного оператора
Пусть задан линейный оператор : V→V и
произвольный базис В={b1 , b2 , …, bn } пространства
V, тогда образ (v) произвольного вектора v = c1 b1+ c2 b2+ …+ cn bn из V равняется (v) = c1 (b1) + c2 (b2) + … + cn (bn)С другой стороны, векторы (b1), (b2), …, (bn)являются векторами пространства V, поэтому
(b1) = t11 b1 + t21 b2 + … + tn1 bn
(b2) = t12 b1 + t22 b2 + … + tn2 bn
…………………………………………………………………………..
(bn) = t1n b1 + t2n b2 + … + tnn bn
Слайд 17Матрица линейного оператора
Определение 3.1. Матрица
Называется матрицей линейного оператора в базе
В.
Слайд 184. Подобные матрицы
Пусть даны два базиса В =
и G = векторного пространства V и Р – матрица перехода от базиса В к базису G:
Пусть Т – матрица линейного оператора в базисе В:
,
а S– матрица линейного оператора в базисе В:
Найдем связь между матрицами одного и того же оператора в различных базах.
Слайд 194. Подобные матрицы (продолжение)
Получим
.
Определение 4.1.
Две квадратные матрицы S и T одного размера называются подобными, если найдется невырожденная матрица Р, такая чтоТеорема 4.2. Матрицы линейного оператора в различных базах подобны.