Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Львівський державний університет внутрішніх справ Тема 1 8 : “ Критерій
Содержание
- 1. Львівський державний університет внутрішніх справ Тема 1 8 : “ Критерій
- 2. Варіант11.Записати формулу і дати визначення ймовірності.2. Написати
- 3. Тема 18. «Критерій значущості та перевірка гіпотез» Заняття
- 4. Доводжу план семінару №7Тема 21. Застосування математичних
- 5. Сучасна математична статистика — це наука про прийняття рішень в умовах невизначеності. МАТЕМАТИЧНІ МЕТОДИ У ПСИХОЛОГІЇ
- 6. Питання №1Нульова і альтернативна гіпотези та їх
- 7. Питання №1Нульова і альтернативна гіпотези та їх
- 8. Питання №1Нульова і альтернативна гіпотези та їх
- 9. Питання №2 Правило формулювання і прийняття гіпотезПриклади
- 10. Питання №2 Правило формулювання і прийняття гіпотезДалі
- 11. Статистичний критерій – метод розрахунку певного
- 12. Статистичний критерій – метод розрахунку певного
- 13. Статистичні критерії поділяють на параметричні і
- 14. Питання №1 Поняття та перелік багатофункціональних критеріїв
- 15. Параметричні критерії вважають потужнішими, ніж непараметричні,
- 16. Питання №2 Вибір параметричних критеріїв залежно від характеру сукупності і досліджуваних завдань
- 17. Питання №2 Вибір параметричних критеріїв залежно від характеру сукупності і досліджуваних завдань
- 18. Схема вибору непараметричного критерію залежно від експериментального плану, кількості вибірок та їх властивостей
- 19. Множину значень критерію, які не суперечать нульовій
- 20. Питання №1 Гіпотези Помилку, яка полягає у
- 21. Питання №1 Основна ідея дисперсійного аналізуПриклад 1:
- 22. Питання №2 Однофакторний і багатофакторний дисперсійний аналізПриклад
- 23. Питання №2 Однофакторний і багатофакторний дисперсійний аналізФормулювання
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Львівський державний університет внутрішніх справ
Тема 18
:
“Критерій значущості та перевірка гіпотез”
КАФЕДРА
ПСИХОЛОГІЇ УПРАВЛІННЯ
Слайд 2Варіант1
1.Записати формулу і дати визначення ймовірності.
2. Написати формулу повної ймовірності.
3.
Що визначає кореляційний аналіз?
4. Графічно відобразити “об’єднання імовірностей”.
МАТЕМАТИЧНІ МЕТОДИ У
ПСИХОЛОГІЇВаріант2
1.Записати формулу і числа комбінацій з m по n.
2. Написати формулу ймовірності появи хоча б одної події.
3. Що визначає факторний аналіз?
4. Графічно відобразити зворотній слабкий кореляційний зв’язок.
Слайд 3Тема 18. «Критерій значущості та перевірка гіпотез»
Заняття 1. „Гіпотези у
психологічних дослідженнях”.
Навчальні питання:
Нульова і альтернативна гіпотези та їх перевірка.
Правило формулювання і прийняття гіпотезНавчальна література:
1. Іванюта І.Д., Рибалка В.І., Рудоміно-Дусятська І.А.. Елементи теорії ймовірностей та математичної статистики.- Київ-2003, стр 157-205.
2. Барковський В.В., Барковська Н.В., Лопатін О.К. . Теорія ймовірностей та математична статистика. – Київ-2006, стр.153-220.
МАТЕМАТИЧНІ МЕТОДИ У ПСИХОЛОГІЇ
Слайд 4Доводжу план семінару №7
Тема 21. Застосування математичних методів у різних
галузях психології
Навчальні питання семінару.
1. Інтерпретація даних факторного аналізу.
2. Використання
результатів факторного і дисперсійного аналізу досліджень в практичній роботі психолога.Реферат на тему: «Застосування математичних методів у виявленні девіантної поведінки працівників правоохоронних органів»
МАТЕМАТИЧНІ МЕТОДИ У ПСИХОЛОГІЇ
Слайд 5Сучасна математична статистика — це наука про прийняття рішень в
умовах невизначеності.
МАТЕМАТИЧНІ МЕТОДИ У ПСИХОЛОГІЇ
Слайд 6Питання №1
Нульова і альтернативна гіпотези та їх перевірка
Статистичною гіпотезою
будемо називати припущення про вид або параметри розподілу деякої ознаки
генеральної сукупності.Розрізняють два види статистичних гіпотез про параметри розподілу:
Гіпотези першого типу стверджують, що невідомий параметр набуває певного значення (або належить деякому проміжку значень).
Гіпотеза другого типу полягає в тому, що невідомі параметри у двох (або кількох) незалежних вибірках мають однакові значення. Останнє практично означає, що серії експериментів, у яких отримані ці вибірки, здійснювались в однакових умовах.
Слайд 7Питання №1
Нульова і альтернативна гіпотези та їх перевірка
Поряд із
даною статистичною гіпотезою, яку, як правило, називають нульовою Н0 (оскільки
в більшості випадків вона стверджує, що відхилення значення досліджуваного параметра від заданого числа дорівнює нулю), розглядають альтернативну гіпотезу Н1, котра є запереченням нульової.Приклади формулювання гіпотез у психології:
Нульова – звязку між рівнем домагань і успішністю особистості немає (або коеф. корел. =0)
Альтернативна – зв’язок є між рівнем домагань і успішністю (або коеф. корел. більше (меньше) 0).
Слайд 8Питання №1
Нульова і альтернативна гіпотези та їх перевірка
Статистичні критерії
підрозділяють на такі категорії:
Критерій значущості. Перевірка за значущістю припускає перевірку
гіпотези про числові значення відомого закону розподілуКритерій узгодженості. Перевірка на узгодженість має на увазі, що випадкова величина, що досліджується,підкорюється закону, що розглядається. Критерій узгодженості можна також сприймати, як критерій значущості.
Критерій однорідності. При перевірці на однорідність випадкові величини досліджуються на факт взаємної відповідності їх законів розподілу (чи підкорюються ці величини одному і тому ж закону). Використовуються у Факторному аналізі для визначення наявності залежностей.
Цей розділ умовний, і часто один і той же критерій може бути використаний в різних якостях.
Слайд 9Питання №2
Правило формулювання і прийняття гіпотез
Приклади формулювання гіпотез у
психології:
1)
Нульова – звязку між рівнем домагань і успішністю особистості немає
(або коеф. корел. =0)Альтернативна – зв’язок є між рівнем домагань і успішністю (або коеф. корел. більше (меньше) 0).
2)
Нульова – дві вибірки одинакові по розподілу (мають одинаковий розмах, середні значення)
Альтернативна – вибірки неодинакові
Слайд 10Питання №2
Правило формулювання і прийняття гіпотез
Далі будується процедура перевірки
гіпотези (критерій згоди) — правило, яке дозволяє за даними спостережень
приймати гіпотезу або відхиляти її (тобто приймати альтернативну гіпотезу).Для цього вибирають статистичний критерій — випадкову величину, яка є статистикою вибірки. Розрізняють параметричні і непараметричні критерії. Якщо статистичний критерій залежить від параметрів розподілу досліджуваної величини, то його називають параметричним. Непараметричні критерії не залежать від параметрів розподілу досліджуваної величини
Вважається, що розподіл критерію відомий.
Слайд 11 Статистичний критерій – метод розрахунку певного числа, яке позначають
як емпіричне значення критерію.
(наприклад: tемп для t-критерію Стьюдента).
Співвідношення емпіричного
і критичного значень критерію є підставою для підтвердження чи спростування гіпотези. Наприклад, у разі застосування t-критерію Стьюдента, якщо tемп > tкр то нульову гіпотезу відхиляють (приймають альтернативну). Питання №2
Правило формулювання і прийняття гіпотез
Слайд 12 Статистичний критерій – метод розрахунку певного числа, яке позначають
як емпіричне значення критерію.
(наприклад: tемп для t-критерію Стьюдента).
Співвідношення емпіричного
і критичного значень критерію є підставою для підтвердження чи спростування гіпотези. Наприклад, у разі застосування t-критерію Стьюдента, якщо tемп > tкр то нульову гіпотезу відхиляють (приймають альтернативну). Питання №2
Правило формулювання і прийняття гіпотез
Слайд 13 Статистичні критерії поділяють на параметричні і непараметричні
До параметричних належать
показники розподілу (середні, дисперсії): - z-критерій
- t-критерій Стьюдента
F-критерій Фішера.
Непараметричні –
засновані на операціях з частотами або рангами:- Q-критерій Розенбаума.
- U-критерій Манна-Вітні;
-T-критерій Вілкоксона;
Питання №2
Правило формулювання і прийняття гіпотез
Слайд 15 Параметричні критерії вважають потужнішими, ніж непараметричні, якщо:
- ознака
виміряна за інтервальною шкалою;
- нормально розподілена.
Якщо розподіл ознаки
відрізняться від нормального - використовують непараметричні критерії. Вони не мають усіх цих обмежень і не потребують тривалих і складних розрахунків.
Порівняно з параметричними, вони обмежені лише в одному – з їх допомогою неможливо оцінити взаємодію двох і більше факторів, що впливають на зміну ознаки. Такі завдання розв’язують лише шляхом двофакторного дисперсійного аналізу.
Питання №2
Правило формулювання і прийняття гіпотез
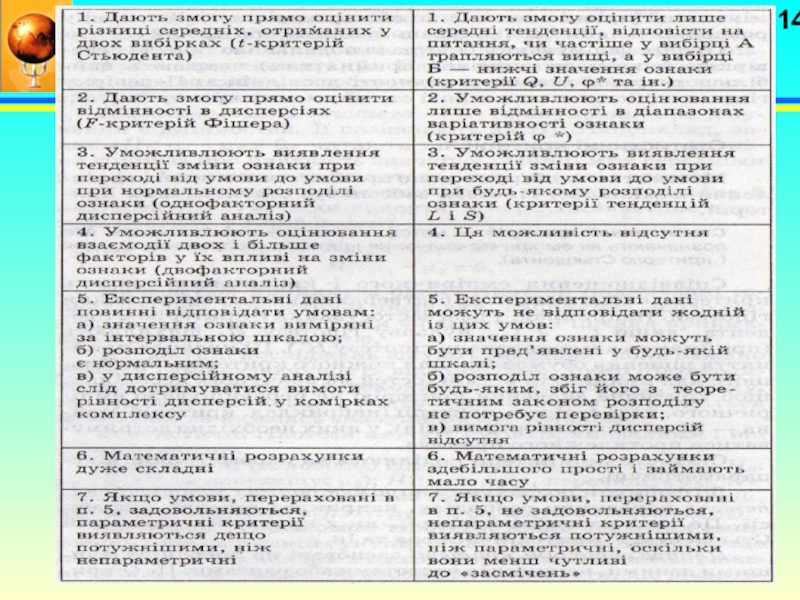
Слайд 16Питання №2
Вибір параметричних критеріїв залежно від характеру сукупності і
досліджуваних завдань
Слайд 17Питання №2
Вибір параметричних критеріїв залежно від характеру сукупності і
досліджуваних завдань
Слайд 18Схема вибору непараметричного критерію залежно від експериментального плану, кількості вибірок
та їх властивостей
Слайд 19Множину значень критерію, які не суперечать нульовій гіпотезі називають областю
допустимих значень, а множину решти значень — критичною областю.
Точки,
які відділяють область допустимих значень від критичної області називають критичними точками. Слайд 20Питання №1
Гіпотези
Помилку, яка полягає у відхиленні нульової гіпотези
(прийнятті альтернативної гіпотези), коли вона правильна, називають помилкою першого роду,
а помилку, яка полягає у прийнятті нульової гіпотези, коли вона хибна, — помилкою другого роду.Ймовірність помилки першого роду називають рівнем значущості критерію,
ймовірність помилки другого роду — його оперативною характеристикою.
Величину 1 – називають надійністю критерію, а величину 1 – — його потужністю.
Слайд 21Питання №1
Основна ідея дисперсійного аналізу
Приклад 1: Трьом групам студентів
(по 7 в кожній) промовляли з різною швидкістю (низькою, середньою,
високою) десять слів.Завдання: довести або спростувати припущення про те, що фактор швидкості промовляння слів впливає на показники їх відтворення.
Формулювання гіпотез
Н0 – відмінності в обсязі відтворення слів ( фактор швидкості) не є вираженішими, ніж випадкові відмінності всередині кожної групи,
Н1 – відмінності в обсязі відтворення слів ( фактор швидкості) є вираженішими, ніж випадкові відмінності всередині кожної групи,
Слайд 22Питання №2
Однофакторний і багатофакторний дисперсійний аналіз
Приклад 2: Чотирьом різним
групам студентів (по 5 в кожній) промовляли з різною швидкістю
(низькою, високою) десять слів з різною довжиною.Завдання: довести значущість припущення про те, що між факторами довжини слова (А) і швидкістю їх промовляння спостерігають взаємодію (вплив двох факторів): при великій швидкоcті краще запамятовуються короткі, при низькій – довгі слова..
Формулювання гіпотез
Зважаючи на умови дослідження, необхідно висунути три комплекти неспрямованих гіпотез:
- про вплив фактора А окремо від фактора В;
- про вплив фактора В окремо від фактора А;
- про вплив взаємної дії фактоів А і В.
Слайд 23Питання №2
Однофакторний і багатофакторний дисперсійний аналіз
Формулювання гіпотез
1
Н0– відмінності в
обсязі відтворення слів ( фактор довжини А) не є вираженішими,
ніж випадкові відмінності між показниками,Н1 – відмінності в обсязі відтворення слів ( фактор довжини А і) є більш вираженішими, ніж випадкові відмінності між показниками,
2
Н0– відмінності в обсязі відтворення слів ( фактор швидкості В) не є вираженішими, ніж випадкові відмінності між показниками,
Н1 – відмінності в обсязі відтворення слів ( фактор швидкості) є більш вираженішими, ніж випадкові відмінності між показниками,
3
Н0– вплив фактора А на обсяг відтворення слів однаковий при різних градаціях фактора В і навпаки,
Н1 – вплив фактора А на обсяг відтворення слів різний при різних градаціях фактора В і навпаки