Слайд 2Закон Фарадея
и его связь с законом сохранения энергии
Всякий раз,
когда происходит изменение сцепленного с контуром потока магнитной индукции, в
контуре возникает индукционный ток. Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции, которая определяется только скоростью изменения магнитного потока, т. е.
Ei = -dФ/dt.
Знак минус показывает, что увеличение потока dФ/dt вызывает возникновение э. д. с. Ei < 0, т. е. поле индукционного тока направлено навстречу потоку.
Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.
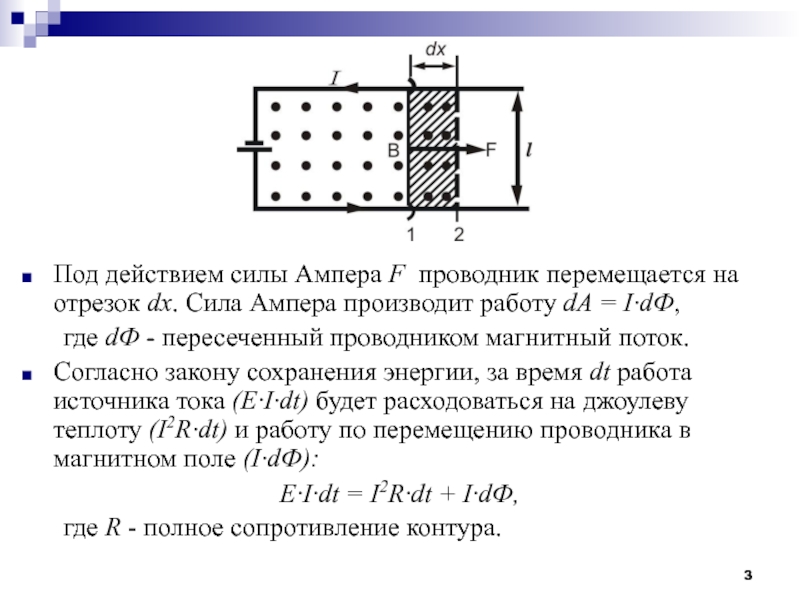
Слайд 3Под действием силы Ампера F проводник перемещается на отрезок dx.
Cила Ампера производит работу dA = I·dФ,
где dФ -
пересеченный проводником магнитный поток.
Согласно закону сохранения энергии, за время dt работа источника тока (E·I·dt) будет расходоваться на джоулеву теплоту (I2R·dt) и работу по перемещению проводника в магнитном поле (I·dФ):
E·I·dt = I2R·dt + I·dФ,
где R - полное сопротивление контура.
Слайд 4Тогда, поделив на I·dt, получим
I = (E – dФ/dt)/R,
где
–dФ/dt = Еi есть не что иное, как закон Фарадея.
Закон
Фарадея можно сформулировать таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Если проводник движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противоположно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления.
Слайд 5Согласно закону Фарадея, возникновение э.д.с. электромагнитной индукции возможно и в
случае неподвижного контура, находящегося в переменном магнитном поле.
Однако сила
Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение э.д.с. индукции.
Максвелл для объяснения э.д.с. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике.
Слайд 6 Вращение рамки в магнитном поле
Явление электромагнитной индукции применяется для преобразования
механической энергии в энергию электрического тока с помощью генератора.
Предположим, что
рамка вращается в однородном магнитном поле (В = const) равномерно с угловой скоростью = const. Магнитный поток, сцепленный с рамкой площадью S, в любой момент времени t равен
Ф = Bn·S = B·S·cosa = B·S·cost,
где a = t - угол поворота рамки в момент времени t (начало отсчета выбрано так, чтобы при t = 0 было а = 0).
Слайд 7При вращении рамки в ней будет возникать переменная э.д.с. индукции
Ei = -dФ/dt = B·S··sint,
При sint = 1 э.д.с. Ei
максимальна, т. е. Emax = B·S·.
Тогда выражение для э.д.с. самоиндукции можно записать в виде
Ei = Emax·sint,
Таким образом, если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная э.д.с., изменяющаяся по гармоническому закону.
В России принята стандартная частота тока
f = /(2) = 50 Гц,
поэтому изменения Emax возможно лишь варьирование B и S.
Слайд 8Для увеличения магнитной индукции В:
- применяют мощные постоянные магниты;
- через
электромагниты пропускают значительный ток;
- внутрь электромагнита помещают сердечники из материалов
с большой магнитной проницаемостью m.
Если вращать не один, а ряд витков, соединенных последовательно, то тем самым увеличивается S.
Процесс превращения механической энергии в электрическую обратим.
Если по рамке, помещенной в магнитное поле, пропускать электрический ток, то на нее будет действовать вращающий момент, и рамка начнет вращаться.
На этом принципе основана работа электродвигателей.
Слайд 9Индуктивность контура. Самоиндукция
Электрический ток, текущий в замкнутом контуре, создает вокруг
себя магнитное поле, индукция которого, по закону Био-Савара-Лапласа, пропорциональна току.
Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре:
Ф = L·I, (1)
где коэффициент пропорциональности L называется индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с.
Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Слайд 10Из выражения (1) определяется единица индуктивности генри (Гн): 1 Гн -
индуктивность такого контура, магнитный поток самоиндукции которого при токе в
1 А равен 1 Вб:
1 Гн = 1 Вб/А = 1 В·с/А.
Рассчитаем индуктивность бесконечно длинного соленоида.
Из предыдущей лекции известно, что полный магнитный поток сквозь соленоид (потокосцепление) равен
Подставив это выражение в формулу (1), получим
т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости m вещества, из которого изготовлен сердечник соленоида.
(2)
Слайд 11Индуктивность контура в общем случае зависит только от геометрической формы
контура, его размеров и магнитной проницаемости той среды, в которой
он находится. В этом смысле индуктивность контура - аналог электрической емкости уединенного проводника.
Применяя к явлению самоиндукции закон Фарадея, получим, что э.д.с. самоиндукции
Если контур не деформируется и магнитная проницаемость среды не изменяется, тo L = const и
где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем.
(3)
Слайд 12Если ток со временем возрастает, то
dI/dt > 0 и
εs < 0,
т. е. ток самоиндукции направлен навстречу току,
обусловленному внешним источником, и замедляет его возрастание.
Если ток со временем убывает, то
dI/dt < 0 и εs > 0,
т. е. индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание.
Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.
Слайд 13Токи при размыкании и замыкании цепи
При всяком изменении силы тока
в проводящем контуре возникает э. д. с. самоиндукции, в результате
чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции.
Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки совпадают по направлению с ослабевающим током.
Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. Е, резистор сопротивлением R и катушку индуктивностью L. Под действием внешней э. д. с. в цепи течет постоянный ток
I0 = Е / R.
Слайд 14В момент времени t = 0 отключим источник тока. Ток в
катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с.
самоиндукции
В каждый момент времени ток в цепи определяется законом Ома
I =E /R,
или
Разделив переменные в выражении (4), получим
(4)
Слайд 15Интегрируя это уравнение, находим
где t = L/R - постоянная,
называемая временем релаксации.
Переменная t есть время, в течение которого сила
тока уменьшается в e раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону.
1- изменение тока при
размыкании цепи;
2- изменение тока при
замыкании цепи.
(5)
Слайд 16Взаимная индукция
Рассмотрим два неподвижных контура (1 и 2), расположенных достаточно
близко друг от друга.
Если в контуре 1 течет ток
I1, то магнитный поток, создаваемый этим током (поле на рисунке изображено сплошными линиями), пропорционален I1.
Обозначим через Ф21 ту часть потока, которая пронизывает контур 2. Тогда
Ф21 = L21·I1 (6)
где L21 - коэффициент пропорциональности.
Слайд 17Если ток I1 изменяется, то в контуре 2 индуцируется э.д.с.
Ei2, которая по закону Фарадея равна и противоположна по знаку
скорости изменения магнитного потока Ф21, созданного током в первом контуре и пронизывающего второй.
Эта э.д.с. равна:
Аналогично, при протекании в контуре 2 тока I2 магнитный поток пронизывает первый контур. Если Ф12 - часть этого потока, пронизывающего контур 1, то
Ф12 = L12I2.
Если ток I2 изменяется, то в контуре 1 индуцируется э.д.с. Ei1, которая равна и противоположна по знаку скорости изменения магнитного потока Ф12, созданного током во втором контуре и пронизывающего первый:
Слайд 18Явление возникновения э.д.с. в одном из контуров при изменении силы
тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L12 и
L21 называются взаимной индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что L12 и L21 равны друг другу, т. е.
L12 = L21. (7)
Рассчитаем взаимную индуктивность двух катушек, намотанных на общий тороидальный сердечник. Этот случай имеет большое практическое значение.
Слайд 19Магнитная индукция поля, создаваемого первой катушкой с числом витков N1,
током I1 и магнитной проницаемостью m сердечника, равна
где l -
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй катушки
Тогда полный магнитный поток (потокосцепление) сквозь вторичную обмотку, содержащую N2 витков,
Слайд 20Поток создается током I1, поэтому, согласно (7),
получаем
Если вычислить
магнитный поток, создаваемый катушкой 2 сквозь катушку 1, то для
L12 получим выражение в соответствии с формулой (8).
Таким образом, взаимная индуктивность двух катушек, намотанных на общий тороидальный сердечник,
(8)
Слайд 21Трансформаторы, основные соотношения
Принципиальная схема трансформатора показана на рисунке.
Первичная и вторичная
катушки (обмотки), имеющие соответственно N1 и N2 витков, укреплены на
замкнутом железном сердечнике. Так как концы первичной обмотки присоединены к источнику переменного напряжения с э.д.с. E1 , то в ней возникает переменный ток I1 , создающий в сердечнике трансформатора переменный магнитный поток Ф.
Слайд 22Этот поток практически полностью локализован в железном сердечнике и, следовательно,
почти целиком пронизывает витки вторичной обмотки.
Изменение этого потока вызывает
во вторичной обмотке появление э.д.с. взаимной индукции, а в первичной - э.д.с. самоиндукции.
Ток I1 первичной обмотки определяется согласно закону Ома:
где R1 - сопротивление первичной обмотки.
Падение напряжения I1R1 на сопротивлении R1 при быстропеременных полях мало по сравнению с каждой из двух э.д.с., поэтому
(9)
Слайд 23Э.д.с. взаимной индукции, возникающая во вторичной обмотке,
Сравнивая выражения (18.9) и (18.10), получим, что э.д.с., возникающая
во вторичной обмотке, равна
где знак минус показывает, что э.д.с. в первичной и вторичной обмотках противоположны по фазе.
Отношение числа витков N2/N1, показывающее, во сколько раз э.д.с. во вторичной обмотке трансформатора больше (или меньше), чем в первичной, называется коэффициентом трансформации.
(10)
(11)
Слайд 24Пренебрегая потерями энергии, которые в современных трансформаторах не превышают 2 %
и связаны в основном с выделением в обмотках джоулевой теплоты
и появлением вихревых токов, и применяя закон сохранения энергии, можем записать, что мощности тока в обеих обмотках трансформатора практически одинаковы:
откуда, учитывая соотношение (11), найдем
т. е. токи в обмотках обратно пропорциональны числу витков в этих обмотках.
(12)
Слайд 25Если N2/N1 > 1, то имеем дело с повышающим трансформатором,
увеличивающим переменную э.д.с. и понижающим ток (применяются, например, для передачи
электроэнергии на большие расстояния, так как в данном случае потери на джоулеву теплоту, пропорциональные квадрату силы тока, снижаются).
Если N2/N1 < 1, то имеем дело с понижающим трансформатором, уменьшающим э.д.с. и повышающим ток (применяются, например, при электросварке, так как для нее требуется большой ток при низком напряжении).
Трансформаторы, используемые в радиоустройствах, имеют 4-5 обмоток, обладающих разными рабочими напряжениями.
Трансформатор, состоящий из одной обмотки, называется автотрансформатором. В случае повышающего автотрансформатора э.д.с. подводится к части обмотки, а вторичная э.д.с. снимается со всей обмотки.
Слайд 26Энергия магнитного поля
Проводник, по которому протекает электрический ток, всегда окружен
магнитным полем. Магнитное поле, подобно электрическому, является носителем энергии. Естественно
предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.
Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток Ф = L·I, причем при изменении тока на dI магнитный поток изменяется на dФ = L·dI.
Однако для изменения магнитного потока на величину dФ необходимо совершить работу dA = I·dФ = L·I·dI. Тогда работа по созданию магнитного потока Ф равна
(13)
Слайд 27Следовательно, энергия магнитного поля, связанного с контуром,
Энергию магнитного поля можно
представить как функцию величин, характеризующих это поле в окружающем пространстве.
Для этого рассмотрим частный случай - однородное магнитное поле внутри длинного соленоида.
Подставив в формулу (14) выражение (2), получим
(14)
(15)
то
где S·l = V - объем соленоида.
Магнитное поле соленоида однородно
и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью
(16)
(17)
Слайд 29Вопросы на семинар:
1. Закон Фарадея и его связь с законом
сохранения энергии.
2. Вращение рамки в магнитном поле.
3. Индуктивность контура. Самоиндукция
4.
Токи при размыкании и замыкании цепи.
5. Взаимная индукция.
6. Трансформаторы, основные соотношения.
7. Энергия магнитного поля.