Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ Часть 3 – ТРАНСПОРТНАЯ ЗАДАЧА
Содержание
- 1. МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ Часть 3 – ТРАНСПОРТНАЯ ЗАДАЧА
- 2. Транспортная задача
- 3. Транспортная задача(1)
- 4. Транспортная задачаСумма запасов продукции во всех пунктах
- 5. Транспортная задачаЕсли суммарные запасы превышают суммарные потребности,
- 6. Транспортная задачаЗАДАЧАЗаводы некоторой автомобильной фирмы расположены в
- 7. Транспортная задачаОпределение переменныхОбозначим количество автомобилей, перевозимых из
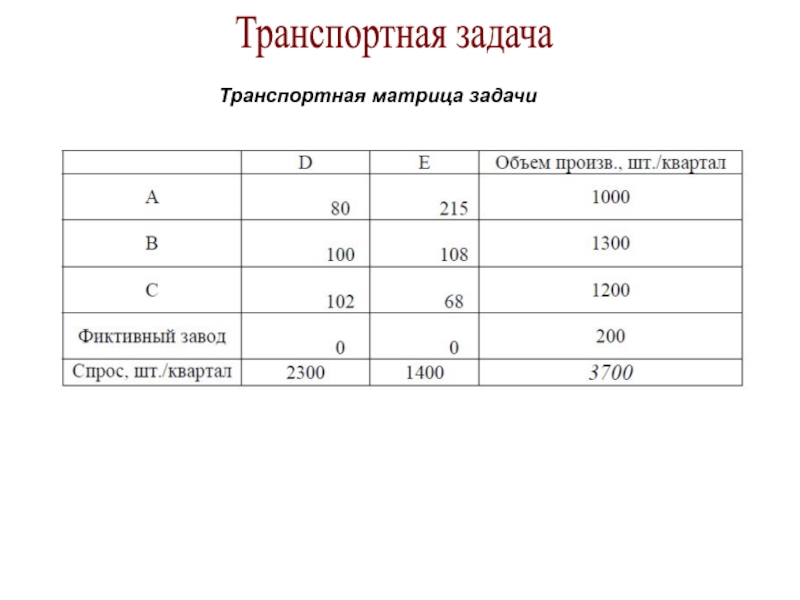
- 8. Транспортная задачаТранспортная матрица задачи
- 9. Транспортная задачаЗадание ЦФСуммарные затраты в рублях на ежеквартальную перевозку автомобилейопределяются по формуле
- 10. Транспортная задачаМЕТОДЫ НАХОЖДЕНИЯ ОПОРНЫХ ПЛАНОВОпорный план является
- 11. Транспортная задачаМетод северо-западного углаНа каждом шаге метода
- 12. Транспортная задача
- 13. Транспортная задача
- 14. Транспортная задача
- 15. Транспортная задачаЗАДАЧАПроверка сбалансированности задачи показывает, что суммарный объемзапасов равен суммарному объему потребностей:
- 16. Транспортная задача
- 17. Транспортная задача
- 18. Транспортная задача
- 19. Транспортная задача
- 20. СПАСИБО ЗА ВНИМАНИЕ
- 21. Скачать презентанцию
Транспортная задача
Слайды и текст этой презентации
Слайд 4Транспортная задача
Сумма запасов продукции во всех пунктах отправления должна равняться
суммарной потребности во всех пунктах потребления, т.е.:
(2)
Если (2) выполняется, то
ТЗ называется сбалансированной (закрытой),в противном случае –
несбалансированной (открытой)
Слайд 5Транспортная задача
Если суммарные запасы превышают суммарные потребности, необходим
дополнительный фиктивный (реально
не существующий) пункт потребления,
который будет формально потреблять существующий излишек запасов,
т.е.Если суммарные потребности превышают суммарные запасы, то
необходим дополнительный фиктивный пункт отправления, формально
восполняющий существующий недостаток продукции в пунктах отправления:
Для фиктивных перевозок вводятся фиктивные тарифы cф , величина
которых обычно приравнивается к нулю cф = 0 . Но в некоторых ситуациях
величину фиктивного тарифа можно интерпретировать как штраф, которым
облагается каждая единица недопоставленной продукции. В этом случае
величина cф может быть любым положительным числом.
Слайд 6Транспортная задача
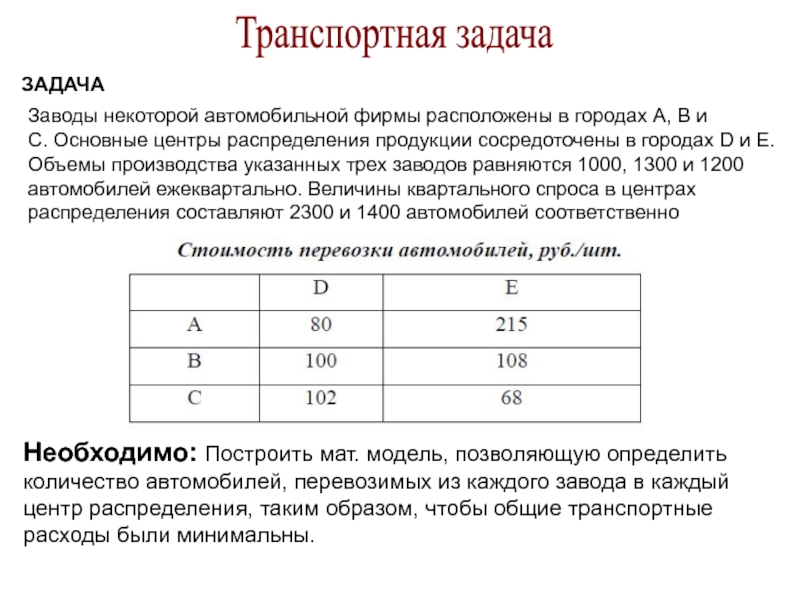
ЗАДАЧА
Заводы некоторой автомобильной фирмы расположены в городах А, В
и
С. Основные центры распределения продукции сосредоточены в городах D и
E.Объемы производства указанных трех заводов равняются 1000, 1300 и 1200
автомобилей ежеквартально. Величины квартального спроса в центрах
распределения составляют 2300 и 1400 автомобилей соответственно
Необходимо: Построить мат. модель, позволяющую определить
количество автомобилей, перевозимых из каждого завода в каждый
центр распределения, таким образом, чтобы общие транспортные
расходы были минимальны.
Слайд 7Транспортная задача
Определение переменных
Обозначим количество автомобилей, перевозимых из i-го завода в
j-й
пункт потребления через .
Проверка сбалансированности задачи
Проверим равенство
суммарного производства автомобилей и суммарного спросаоткуда следует вывод – задача несбалансирована
Слайд 9Транспортная задача
Задание ЦФ
Суммарные затраты в рублях на ежеквартальную перевозку автомобилей
определяются
по формуле
Слайд 10Транспортная задача
МЕТОДЫ НАХОЖДЕНИЯ ОПОРНЫХ ПЛАНОВ
Опорный план является допустимым решением ТЗ
и используется в
качестве начального базисного решения при нахождении оптимального
решения методом
потенциалов. Существует три метода нахождения опорных планов:
метод северо-западного угла;
метод минимального элемента;
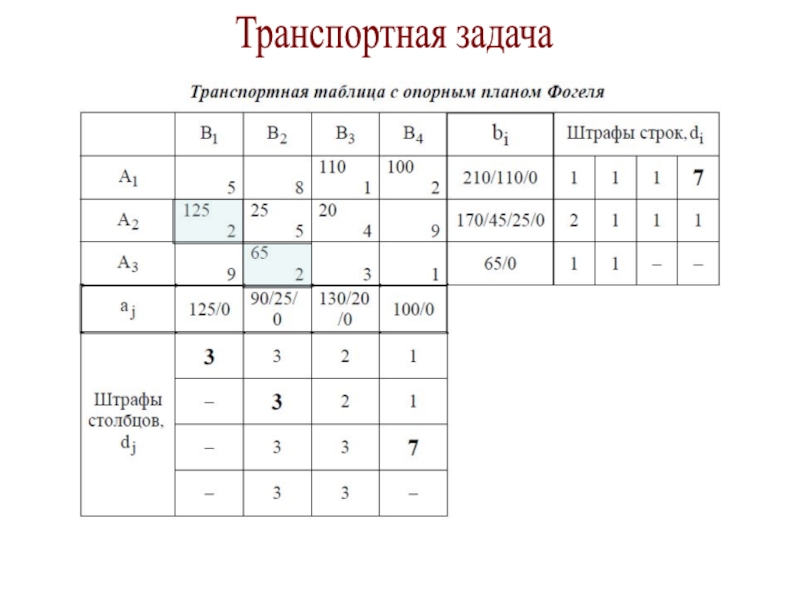
Метод Фогеля.
ВАЖНО !!!
Все существующие методы нахождения опорных планов отличаются только
способом выбора клетки для заполнения
Само заполнение происходит одинаково независимо от используемого метода
Перед нахождением опорного плана транспортная задача должна быть
сбалансирована.
Слайд 11Транспортная задача
Метод северо-западного угла
На каждом шаге метода северо-западного угла из
всех не вычеркнутых
клеток выбирается самая левая и верхняя (северо-западная) клетка.
Слайд 15Транспортная задача
ЗАДАЧА
Проверка сбалансированности задачи показывает, что суммарный объем
запасов равен суммарному
объему потребностей:
