Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Медицинская биостатистика Лекция 1 Статистика в диагностике
Содержание
- 1. Медицинская биостатистика Лекция 1 Статистика в диагностике
- 2. СтатистикаСтатистику можно определить как науку об изучении
- 3. Данные, пример: каковы признаки этой собаки?Качественные:Ее
- 4. Популяция и выборкаВ медицине и в эпидемиологии
- 5. Случайность выборки обуславливает ее репрезентативностьОдин из важнейших
- 6. Имитация многократного вбрасывания игральной кости: программа SUStats.jar http://www.jsc.nildram.co.uk/examples/sustats/SUStats.html
- 7. Простейшая форма закона больших чисел - теорема
- 8. Статистика в диагностикеСтатистический контроль качества диагностических тестов с бинарными исходами
- 9. Что такое «Золотой стандарт» в диагностике?«Золотой стандарт»
- 10. Всё познается в сравненииЗолотой стандарт бывает дорог,
- 11. Статистический анализ – фактически единственный надежный путь
- 12. Основные схемы формирования выборок для статистического контроля
- 13. Пример одновыборочного исследования. Ранняя диагностика рака молочной железы - Маммография
- 14. Массовый маммографический скринингBanks E., Reeves G., Beral
- 15. Результаты массового маммографического скринингаТаблица сопряженности (перекрестной классификации) 2 × 2
- 16. Таблица 2 × 2 – удобная, наглядная
- 17. Основные обозначения для исходов диагностического исследования D
- 18. Таблица 2 х 2: возможные исходы диагностического
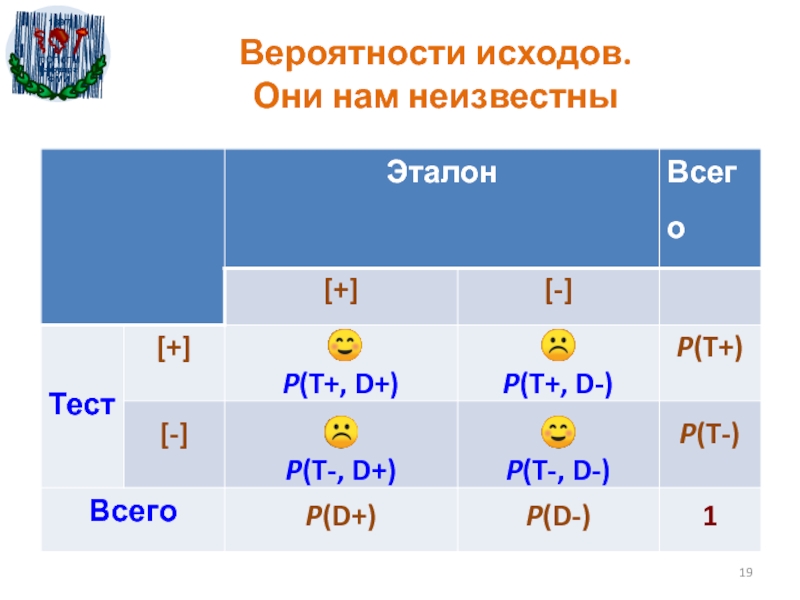
- 19. Вероятности исходов. Они нам неизвестны
- 20. Основная логика статистического оценивания: точечные оценкиОбычно вероятности
- 21. Наблюдаем частоты f(A) (разделим все элементы таблица
- 22. Два основных типа статистических оценокПринципиальной особенностью выборочных
- 23. Точечные оценки долиЧастотническая:Бейзовская:если a priori
- 24. Основная логика статистического оценивания: интервальные оценкиПонятно, что
- 25. Частотнический доверительный интервал и доверительная вероятность- вероятность
- 26. Что такое Доверительный Интервал (ДИ)?100(1 – α)%-й
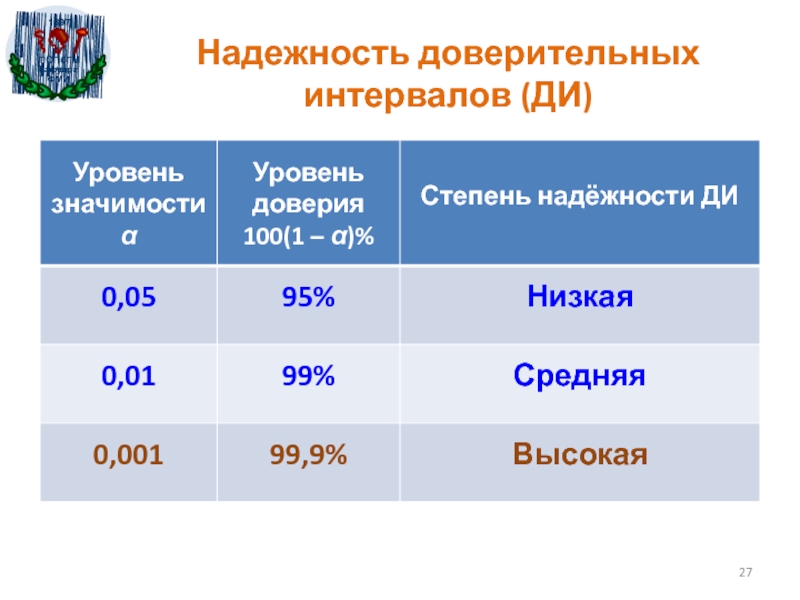
- 27. Надежность доверительных интервалов (ДИ)
- 28. Точность и надежность статистических оценокЧем ýже ДИ,
- 29. ДИИтак, например, 99%-й ДИ означает, что если
- 30. Распознавание и предсказаниеНе существует единого количественного показателя,
- 31. Основные вероятностные показатели распознавательной способности диагностического тестаЧетыре
- 32. Что такое Чувствительность диагностического теста?Чувствительность Se (от
- 33. Что такое Специфичность диагностического теста?Специфичность Sp (от
- 34. Сводка определений основных показателей распознавательной способности проверяемого диагностического теста (ПДТ)
- 35. Идеал и бесполезностьИдеальный тестБесполезный тест (пример)Se +
- 36. Идеальный и бесполезный тесты; значение AUCuninf
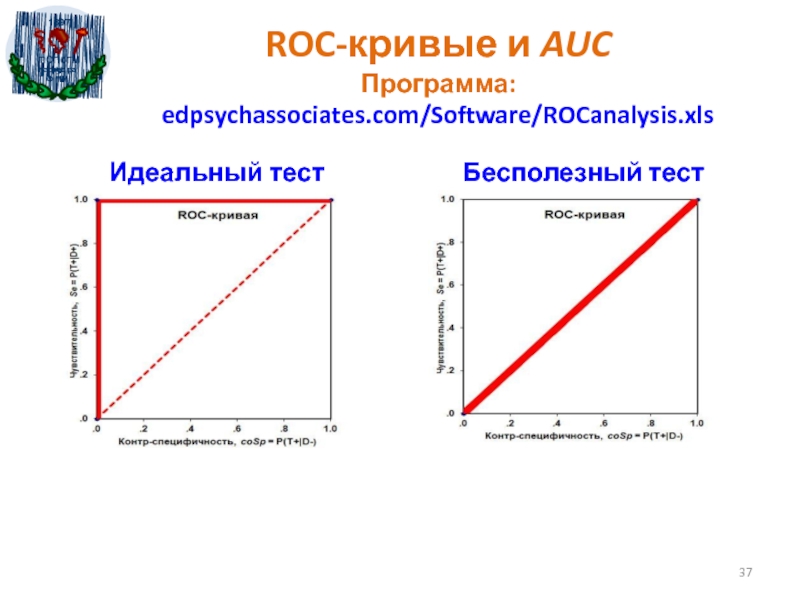
- 37. ROC-кривые и AUC Программа: edpsychassociates.com/Software/ROCanalysis.xlsИдеальный тестБесполезный тест
- 38. Бейзовские точечные оценки показателей распознавательной способности проверяемого диагностического теста (при равномерном приоре)
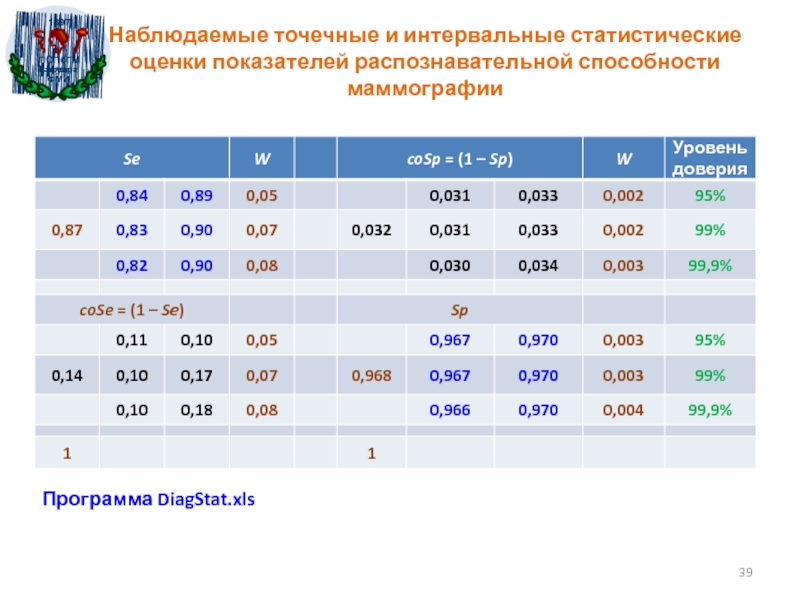
- 39. Наблюдаемые точечные и интервальные статистические оценки показателей распознавательной способности маммографии Программа DiagStat.xls
- 40. Логика использования доверительных интервалов для оценки статистической
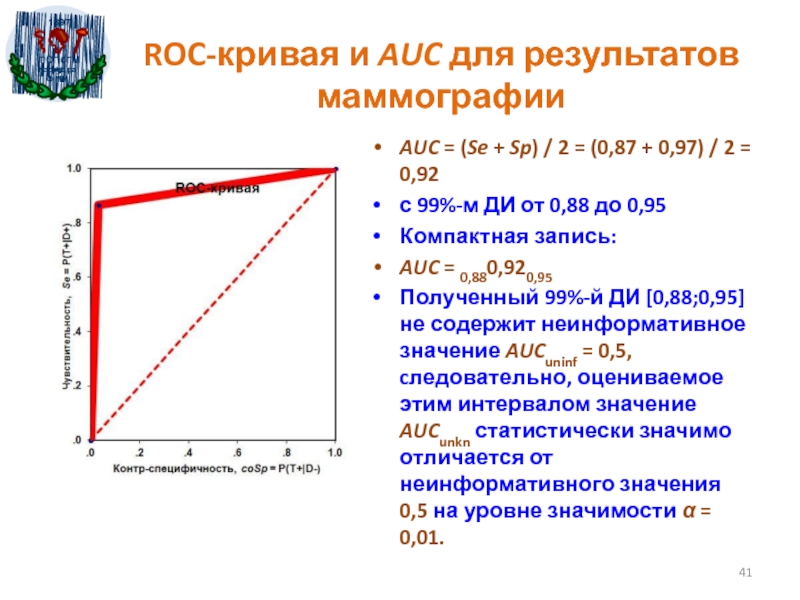
- 41. ROC-кривая и AUC для результатов маммографииAUC =
- 42. Статистическая значимость и информативность Se и SpДля
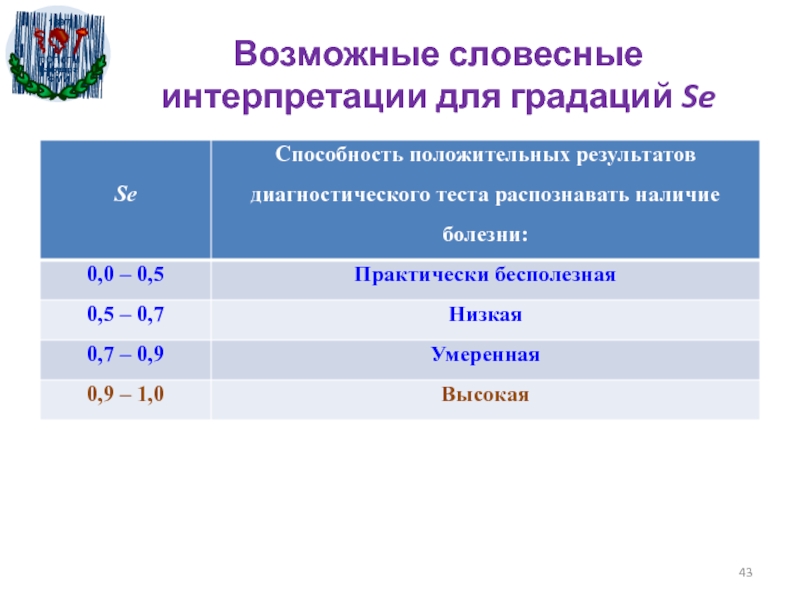
- 43. Возможные словесные интерпретации для градаций Se
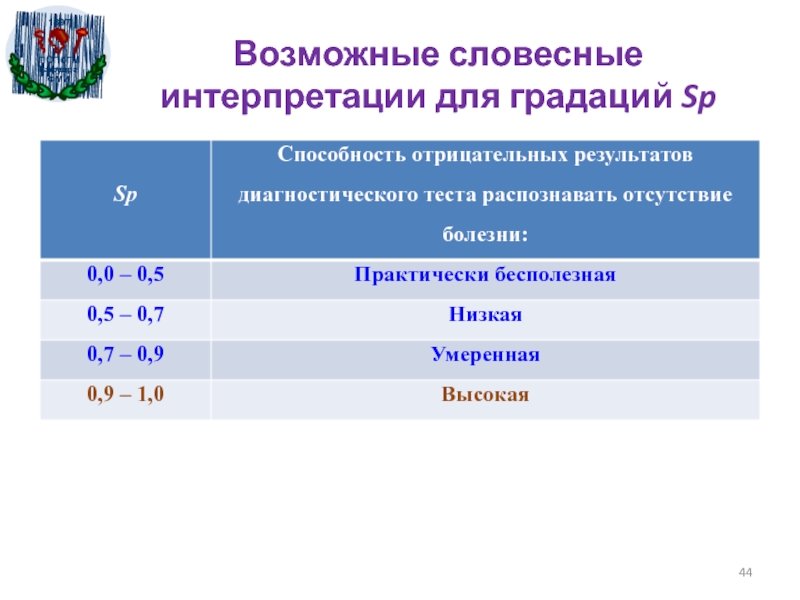
- 44. Возможные словесные интерпретации для градаций Sp
- 45. Когда в нашем распоряжении имеются оценки чувствительности
- 46. Предсказательная способность диагностического теста Получив у данного
- 47. Четыре показателя предсказательной способности образуют две пары
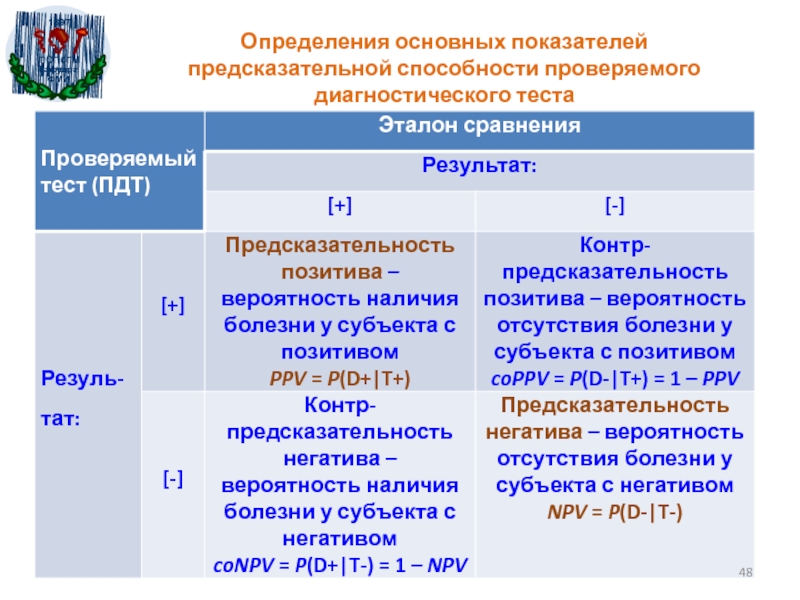
- 48. Определения основных показателей предсказательной способности проверяемого диагностического теста
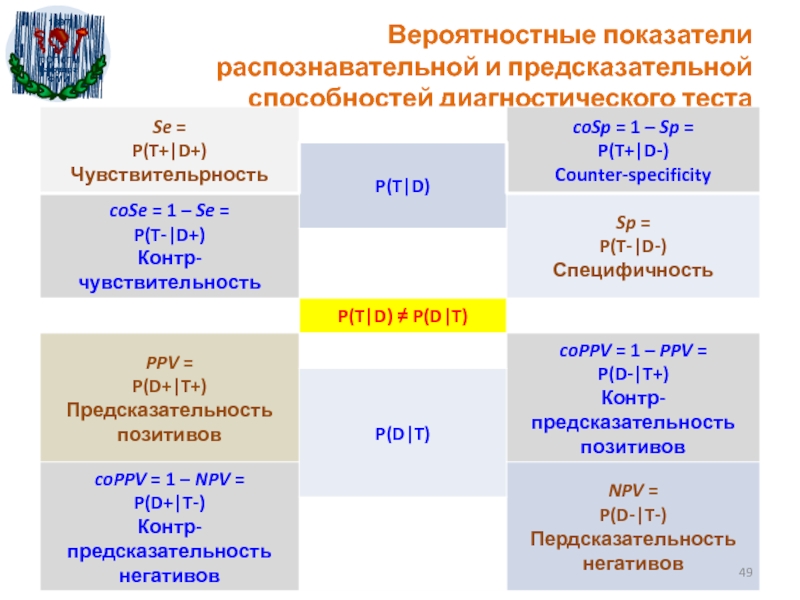
- 49. Вероятностные показатели распознавательной и предсказательной способностей диагностического теста
- 50. Что такое Распространенность болезни, Prev =
- 51. Оценка распространенности болезни при одновыборочном исследованииВероятность обнаружить
- 52. Бейзовские точечные оценки показателей предсказательной способности ПДТ в одновыборочном исследовании (при равномерном приоре)
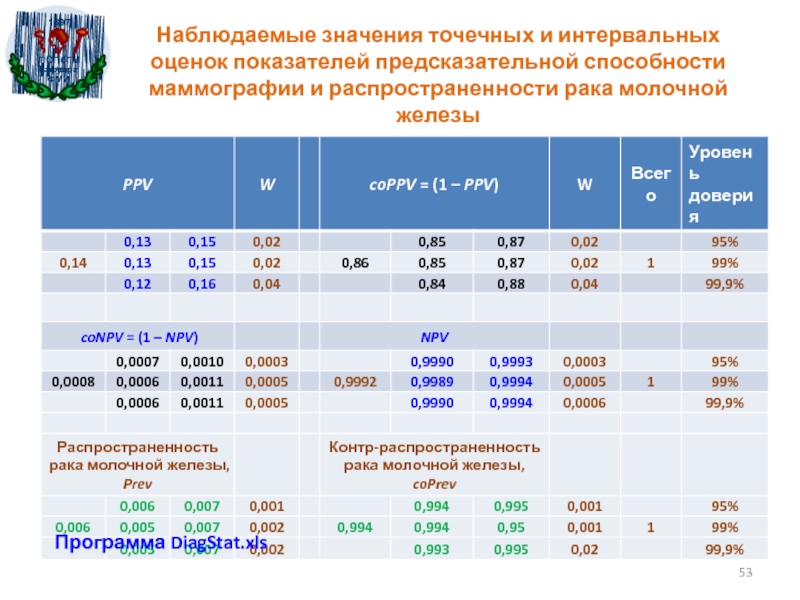
- 53. Наблюдаемые значения точечных и интервальных оценок показателей предсказательной способности маммографии и распространенности рака молочной железыПрограмма DiagStat.xls
- 54. Статистическая значимость отличия PPV от PrevВ данном
- 55. Идеальный и малопригодный тесты в терминах PPV
- 56. Малоинформативные значения показателей предсказательной способности проверяемого диагностического теста (ПДТ)
- 57. Возможные словесные интерпретации для градаций PPV и NPV
- 58. Компактная форма записи для совместного представления точечных
- 59. До и после получения позитиваСтатистическая оценка вероятности
- 60. Контр-прогностичность позитивовОднако оно статистически значимо МЕНЬШЕ неинформативного
- 61. До и после получения негативаСтатистическая оценка вероятности
- 62. Отношения правдоподобийМежду показателями распознавательной и предсказательной способностей
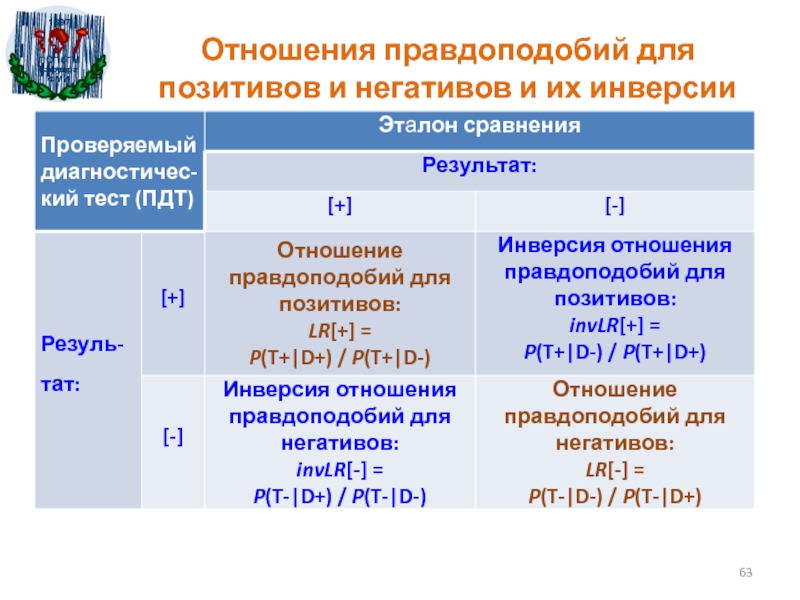
- 63. Отношения правдоподобий для позитивов и негативов и их инверсии
- 64. Идеальный и бесполезный тесты в терминах LR;
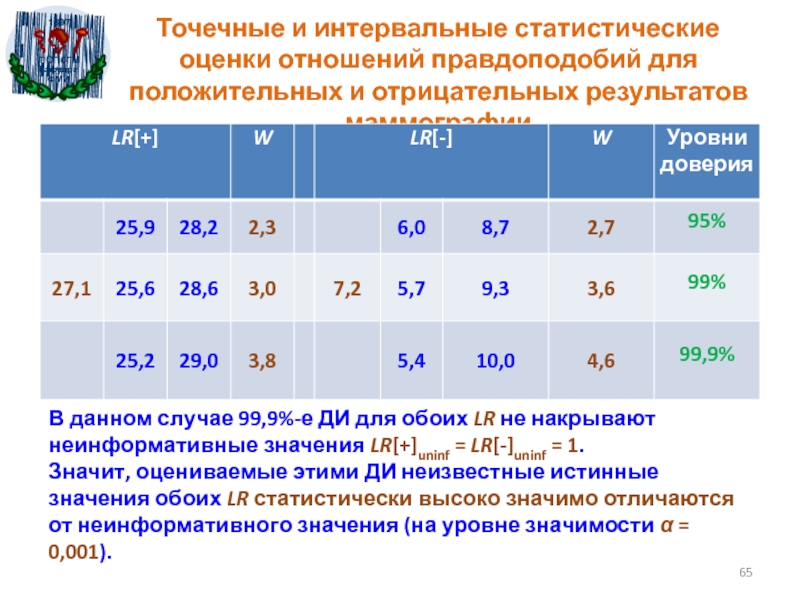
- 65. Точечные и интервальные статистические оценки отношений правдоподобий
- 66. Две интерпретации LR LR[+] показывает, во сколько
- 67. Что такое «шансы за/против» («одды») для случайного
- 68. LR в терминах шансов за/против («оддов»)LR[+] есть
- 69. Слайд 69
- 70. Принятые словесные интерпретации для градаций LR[+] и LR[-]
- 71. Сводка основных полученных результатов по статистическим оценкам
- 72. Полезное правилоГде и когда только возможно, следует
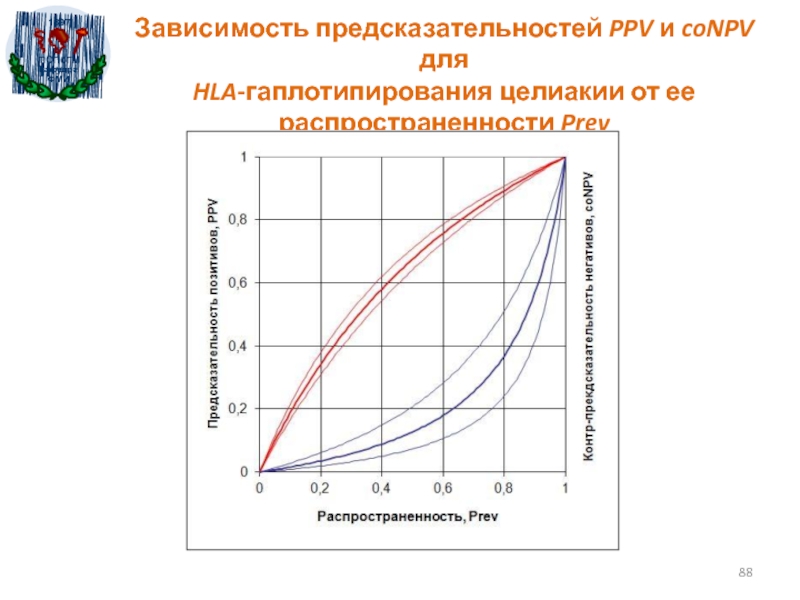
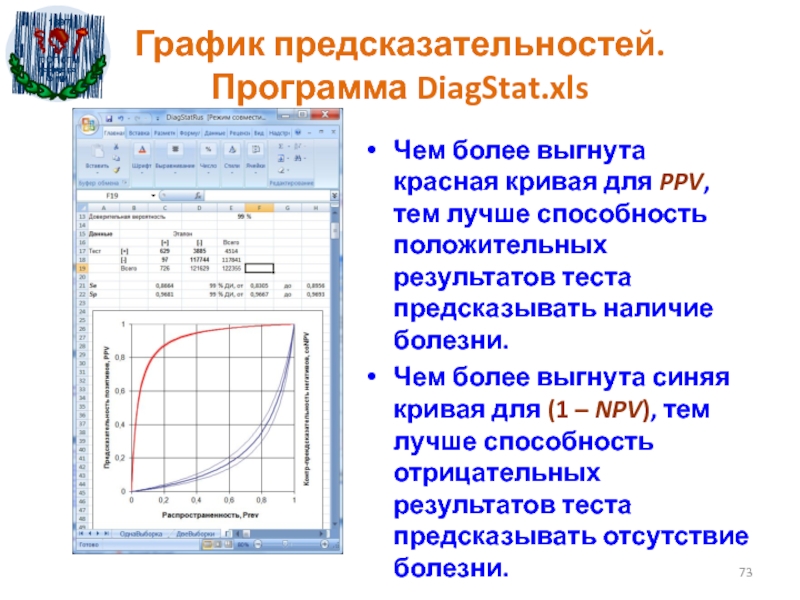
- 73. График предсказательностей. Программа DiagStat.xlsЧем более выгнута
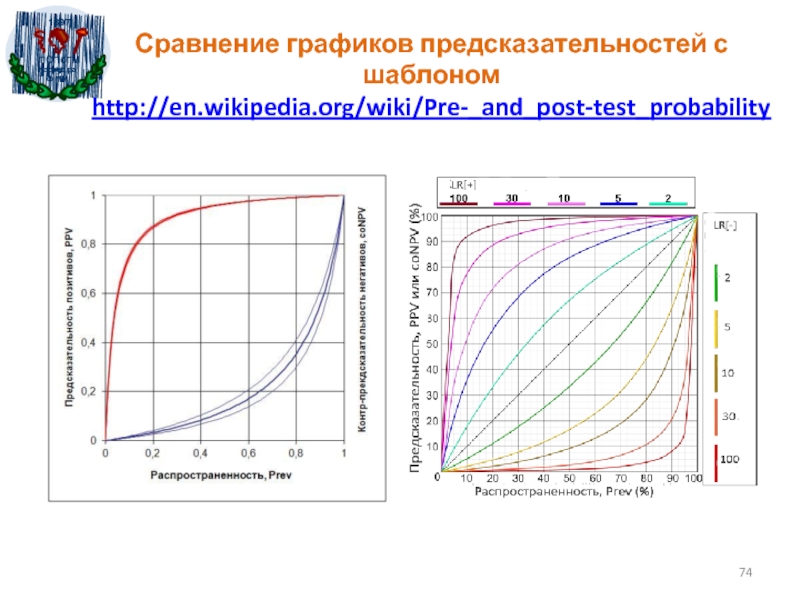
- 74. Сравнение графиков предсказательностей с шаблоном http://en.wikipedia.org/wiki/Pre-_and_post-test_probability
- 75. Предсказательно-информативная распространенность заболевания PPVinfТочечной оценкой предсказательно-информативной распространенности
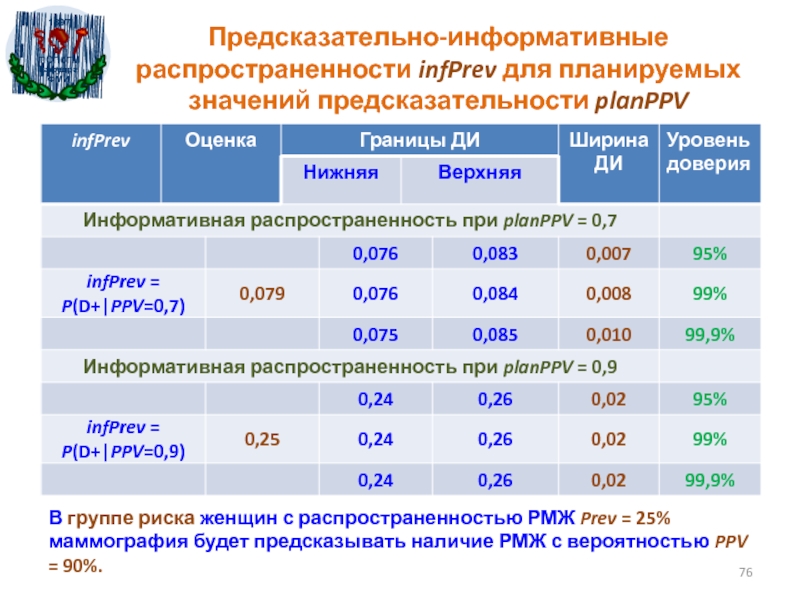
- 76. Предсказательно-информативные распространенности infPrev для планируемых значений предсказательности
- 77. Воспроизводимость результатов маммографии
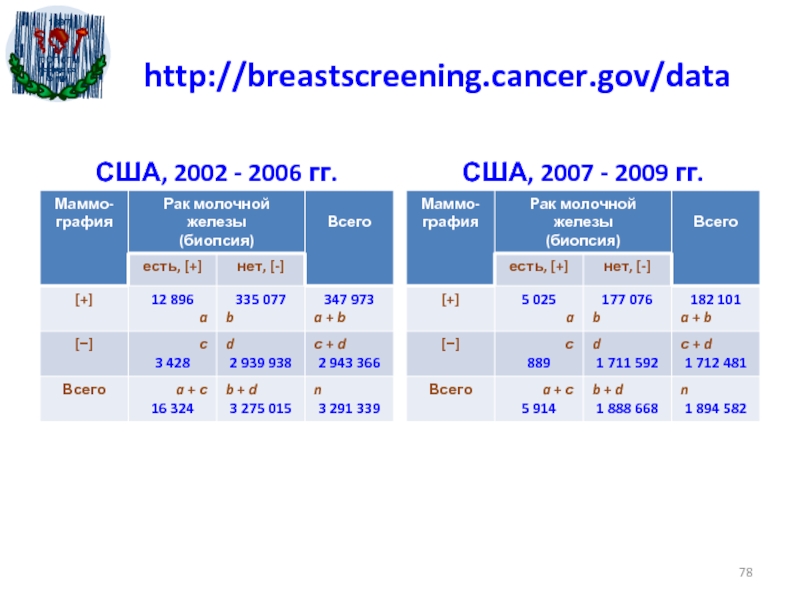
- 78. http://breastscreening.cancer.gov/dataСША, 2002 - 2006 гг.США, 2007 - 2009 гг.
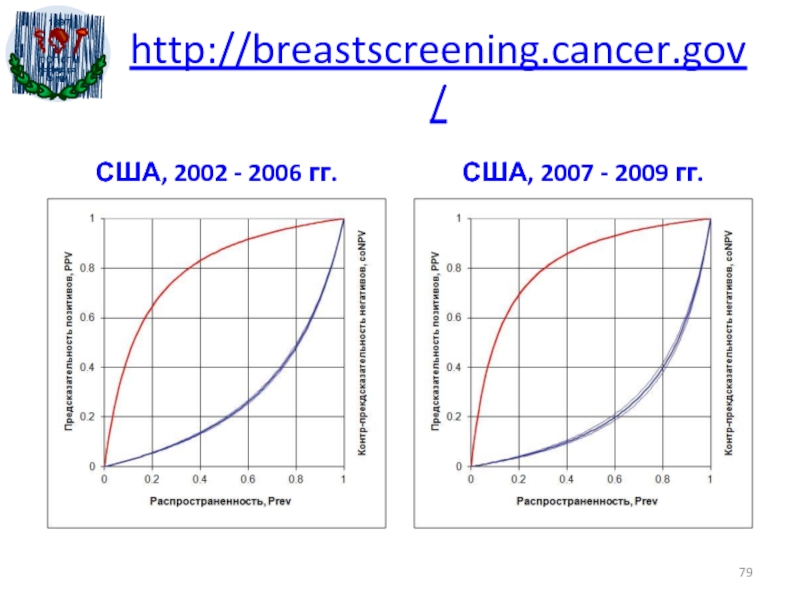
- 79. http://breastscreening.cancer.gov/США, 2002 - 2006 гг.США, 2007 - 2009 гг.
- 80. Двухвыборочное исследование по по схеме «случаи – контроли»
- 81. Что такое исследование типа «случаи –
- 82. ЦелиакияЦелиакия — нарушение пищеварения, которое вызывается некоторыми пищевыми продуктами, содержащими
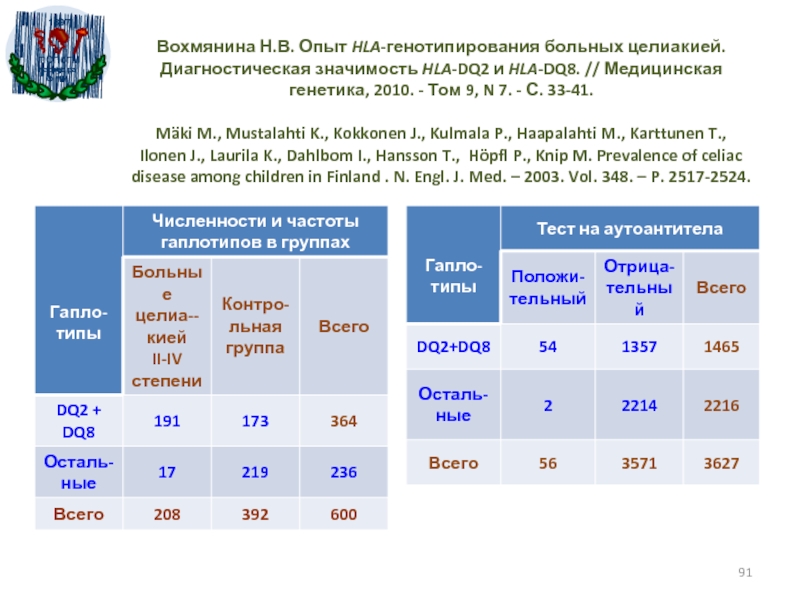
- 83. Вохмянина Н.В. Опыт HLA-генотипирования больных целиакией. Диагностическая
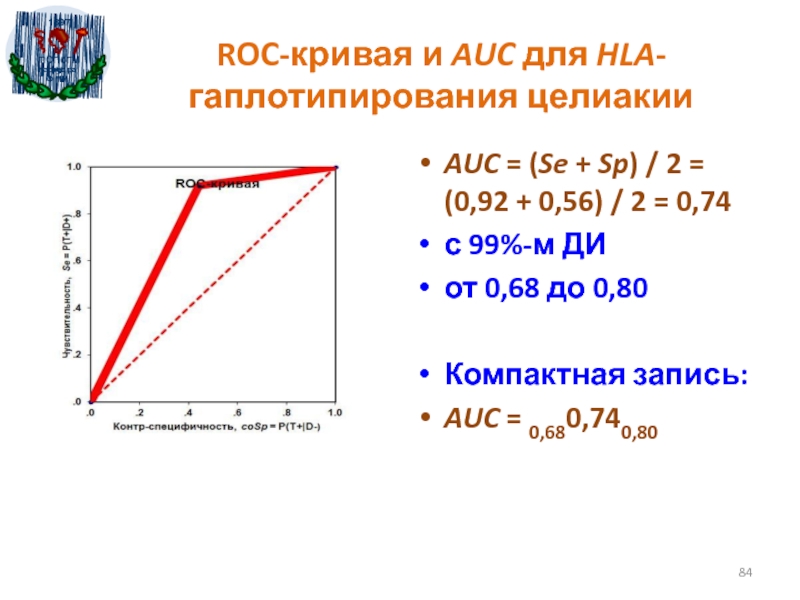
- 84. ROC-кривая и AUC для HLA-гаплотипирования целиакииAUC =
- 85. Предсказательность позитива PPV и негатива NPV в
- 86. Распространенность целиакииДолгое время целиакия считалась редким заболеванием
- 87. Сравнение диагностической и прогностической способностей маммографии и
- 88. Зависимость предсказательностей PPV и coNPV для HLA-гаплотипирования целиакии от ее распространенности Prev
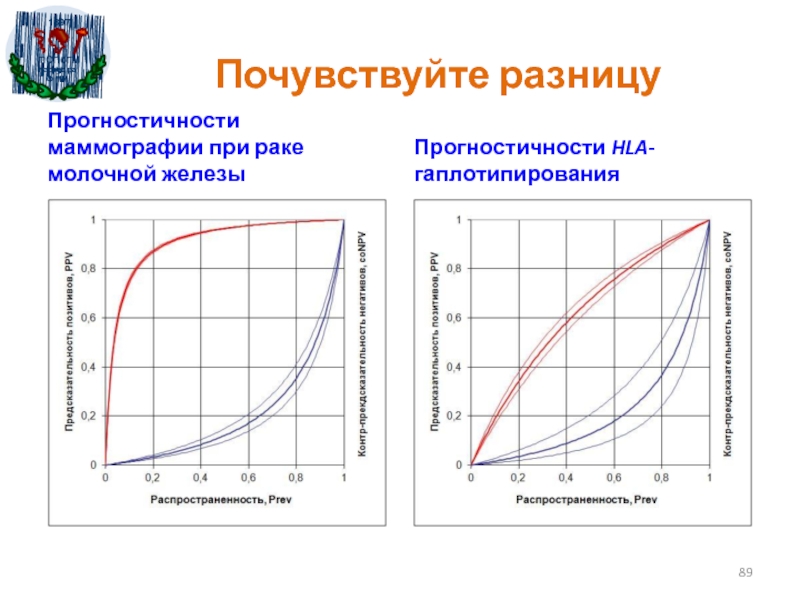
- 89. Почувствуйте разницуПрогностичности маммографии при раке молочной железыПрогностичности HLA-гаплотипирования
- 90. Воспроизводимость результатов применения HLA-гаплотипирования для диагностики целиакии
- 91. Вохмянина Н.В. Опыт HLA-генотипирования больных целиакией. Диагностическая
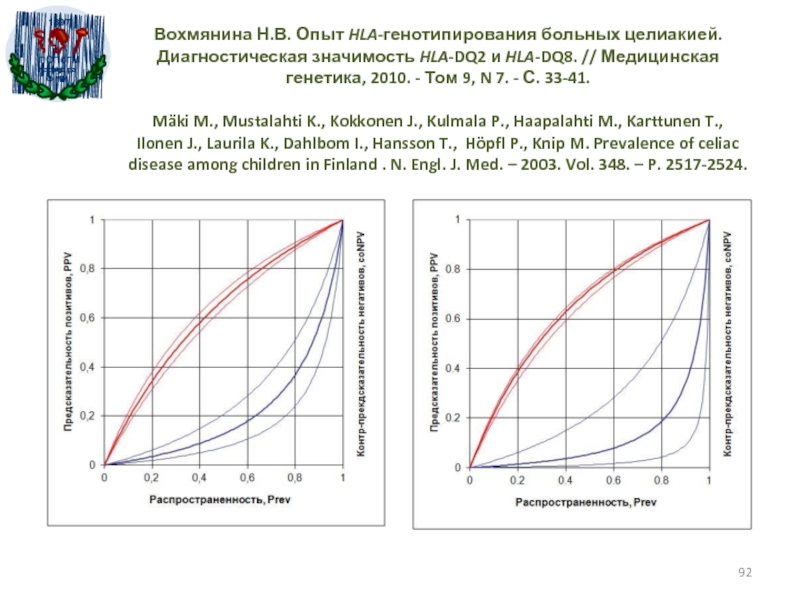
- 92. Вохмянина Н.В. Опыт HLA-генотипирования больных целиакией.
- 93. Галерея графиков предсказательностей
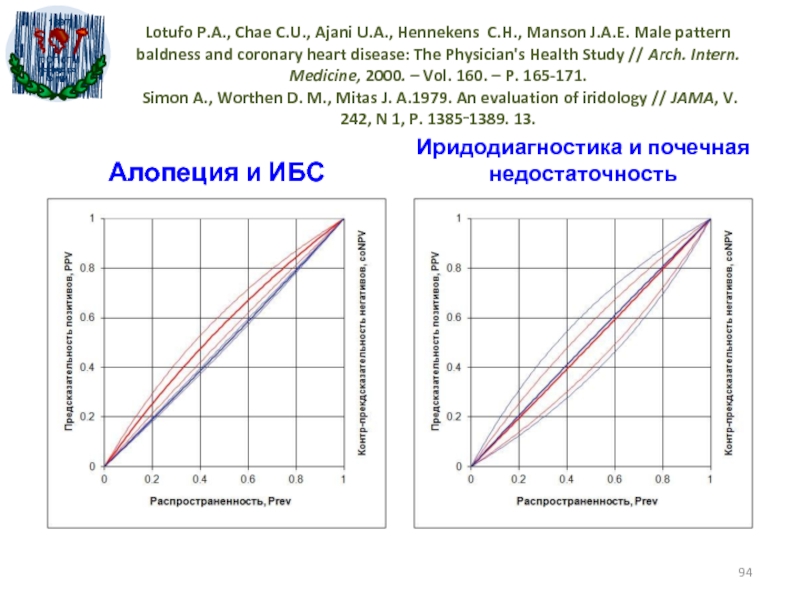
- 94. Lotufo P.A., Chae C.U., Ajani U.A., Hennekens
- 95. Известно, что евнухи, когда они становятся евнухами
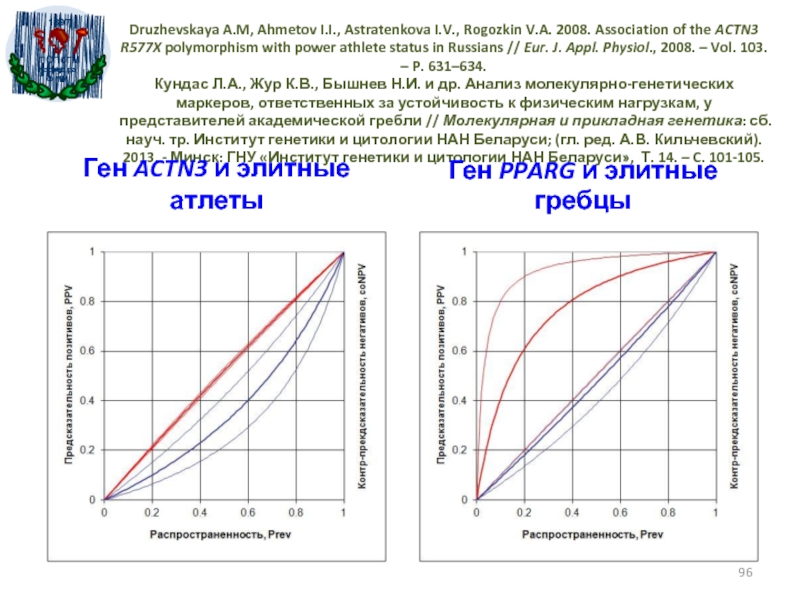
- 96. Druzhevskaya A.M, Ahmetov I.I., Astratenkova I.V., Rogozkin
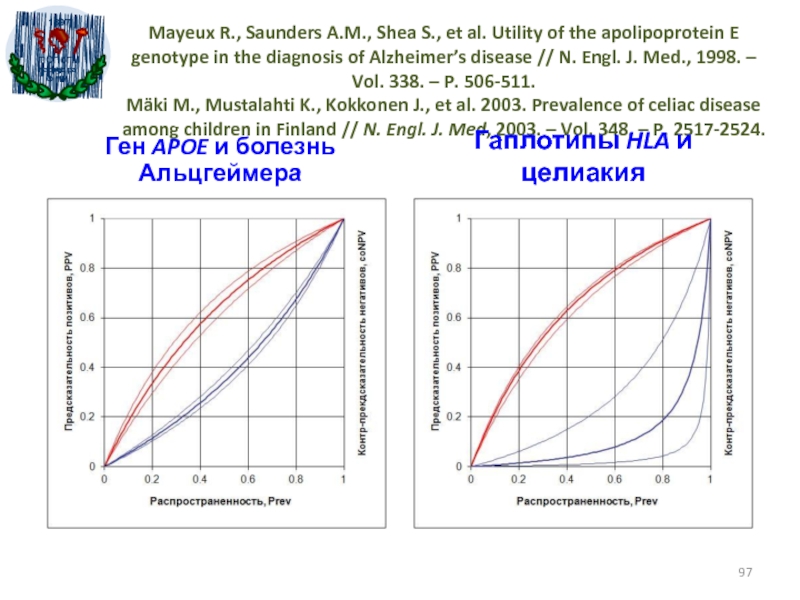
- 97. Mayeux R., Saunders A.M., Shea S., et
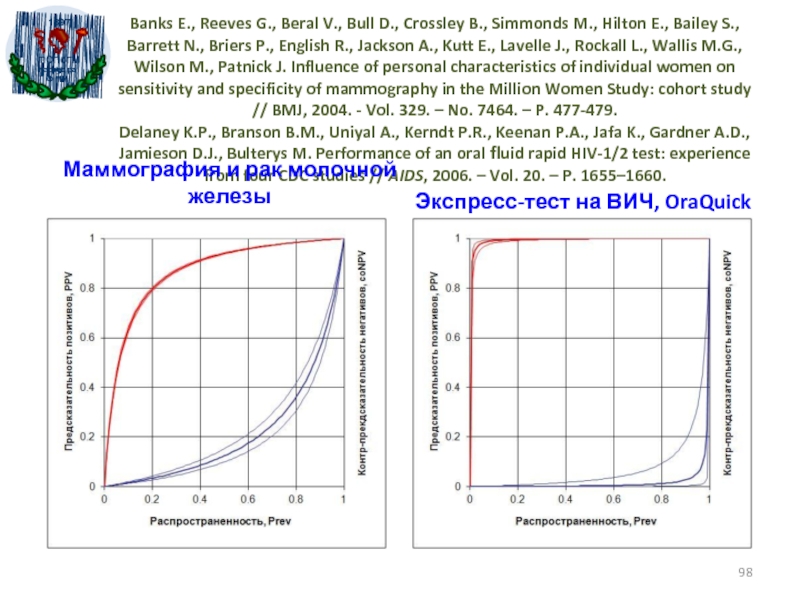
- 98. Banks E., Reeves G., Beral V., Bull
- 99. Скачать презентанцию
СтатистикаСтатистику можно определить как науку об изучении статистических данных иликак науку об
Слайды и текст этой презентации
Слайд 1Медицинская биостатистика
Лекция 1
Статистика в диагностике
Тишков Артем Валерьевич
Кафедра физики, математики и
информатики
Слайд 2Статистика
Статистику можно определить как науку об изучении статистических данных
или
как науку об изменчивости результатов подсчетов и измерений в разных областях научной и практической деятельности человека.
В силу неизбежной изменчивости результатов в биомедицине, фактически все ее выводы и доказательства являются вероятностно-статистическими.
Слайд 3Данные, пример:
каковы признаки этой собаки?
Качественные:
Ее окрас - коричневый с
черным
У нее длинная шерсть
Она энергичная
Количественные:
счетные:
У нее 4 ноги
У нее два
братамерные:
Ее вес – 25,5 кг
Ее рост (в холке) 56,5 см
Слайд 4Популяция и выборка
В медицине и в эпидемиологии термин Популяция является
калькой с английского population - синоним статистического понятия «генеральная совокупность»,
т.е. совокупность индивидуумов, из которой отбирается выборка.Поскольку вероятностной моделью популяции является определенная случайная величина (вероятностная переменная), которая характеризуется определенным распределением, то с этой точки зрения удобно говорить о выборке из данного распределения.
Слайд 5Случайность выборки обуславливает ее репрезентативность
Один из важнейших вопросов, решаемых статистикой:
Действительно
ли данная выборка отражает основные свойства (параметры) распределения, из которого
она извлечена?Другими словами, представительна ли (репрезентативна ли) имеющаяся выборка?
Если выборка случайная, то закон больших чисел (ЗБЧ) гарантирует ее репрезентативность.
ЗБЧ – ОСНОВА ОСНОВ СТАТИСТИКИ
Слайд 6Имитация многократного вбрасывания игральной кости: программа SUStats.jar
http://www.jsc.nildram.co.uk/examples/sustats/SUStats.html
Слайд 7Простейшая форма закона больших чисел - теорема Бернулли
Она утверждает, что
если вероятность события P(A) неизменна во всех испытаниях, то с
увеличением числа испытаний частота события f(A) все ближе сходится к его вероятности, т.е. частота становится все более устойчивой и все меньше отклоняется от вероятности.Следствие:
Мы можем не знать значение вероятности события, но проведя по возможности как можно больше испытаний, мы можем использовать наблюдаемую частоту в качестве надежной статистической оценки этой неизвестной вероятности.
Слайд 8Статистика в диагностике
Статистический контроль качества диагностических тестов с бинарными исходами
Слайд 9Что такое «Золотой стандарт» в диагностике?
«Золотой стандарт» (или эталон сравнения)
– такой диагностический тест, который максимально точно (практически безошибочно) определяет
наличие или отсутствие определенной болезни у пациента.Например, при диагнозе рака одними из наиболее убедительных принято считать результаты гистологической диагностики.
Эталонный метод диагностики совсем не обязательно должен быть единственным. Чаще всего это есть результат применения нескольких диагностических методов.
Слайд 10Всё познается в сравнении
Золотой стандарт бывает дорог, болезнен, рискован и
потому его нецелесообразно (неэкономично) использовать в массовых обследованиях.
Очевидно, что и
врач и пациент воздержатся от его применения, если им будет предложен другой более простой, щадящий, но не менее надежный метод диагностики.Вопрос: как убедиться в надежности нового метода?
Ответ: надо сравнить результаты, получаемые с использованием предлагаемого теста, с результатами золотого стандарта.
Слайд 11Статистический анализ – фактически единственный надежный путь оценки качества и
сравнения диагностических тестов
Диагностические тесты далеко не всегда дают верные ответы,
и поэтому возникает необходимость выразить количественно, насколько точен, надежен и информативен данный тест. Очевидно, что лучший и фактически единственный путь работать с несовершенной информацией – использовать статистические методы и выражать результаты диагноза и прогноза в терминах вероятности.
Поэтому следует осознавать, что диагностические тесты определяют не наличие или отсутствие болезни, но лишь их вероятности.
Слайд 12Основные схемы формирования выборок для статистического контроля качества диагностических тестов
1.
Одновыборочное, когортное (cohort), общепопуляционное - population-based) или поперечно-срезовое одномоментное (cross-sectional)
формирование и исследование выборки. При одновыборочной схеме из данной популяции отбирается одна случайная выборка (когорта) субъектов без использования информации о наличии или отсутствии у них данной болезни.2. Двухвыборочное, при котором формируются две независимые случайные выборки по схеме «случаи – контроли» (case-control).
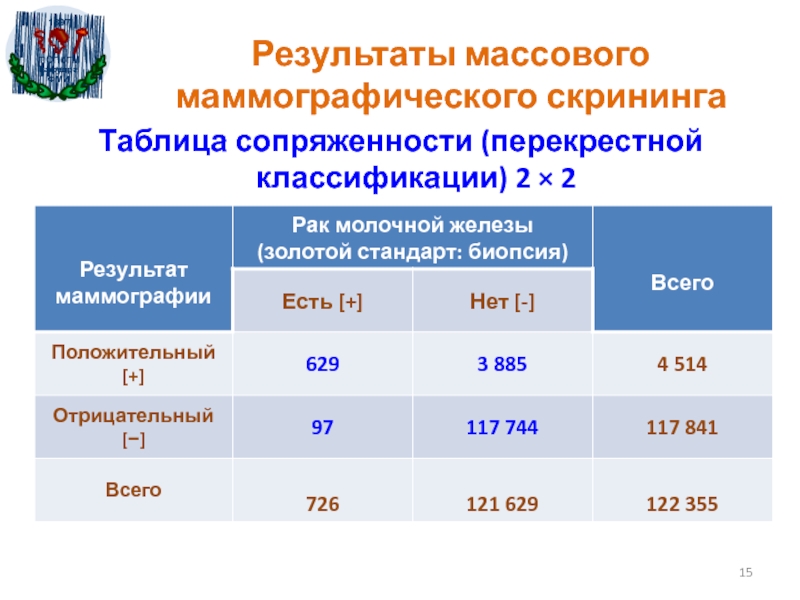
Слайд 14Массовый маммографический скрининг
Banks E., Reeves G., Beral V., Bull D.,
Crossley B., Simmond M., Hilton E., Bailey S., Barret N.,
Briers P., Englis R., Jackson A., Kutt E., Lavelle J., Rockal L., Wallis M.G., Wilson M., Patnick J.Influence of personal characteristics of individual women on sensitivity and specificity of mammography in the Million Women Study: cohort study
BMJ, 2004; Vol. 329; No 7464; p. 477
Слайд 15Результаты массового маммографического скрининга
Таблица сопряженности (перекрестной классификации) 2 × 2
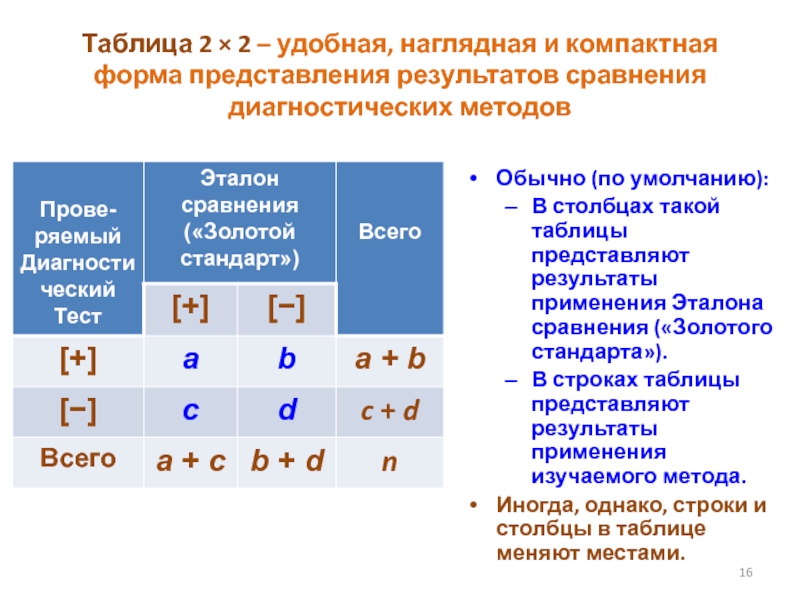
Слайд 16Таблица 2 × 2 – удобная, наглядная и компактная форма
представления результатов сравнения диагностических методов
Обычно (по умолчанию):
В столбцах такой таблицы
представляют результаты применения Эталона сравнения («Золотого стандарта»).В строках таблицы представляют результаты применения изучаемого метода.
Иногда, однако, строки и столбцы в таблице меняют местами.
Слайд 17Основные обозначения для исходов диагностического исследования
D = результаты, полученные
с использованием эталона сравнения (от англ. Disease).
D+ = наличие
болезни по результатам, полученным с использованием эталона сравнения. D- = отсутствие болезни по результатам, полученным с использованием эталона сравнения.
T = результаты, полученные с использованием проверяемого диагностического средства (от англ. Test).
T+ = «позитив», т.е. положительный результат проверяемого теста.
T- = «негатив», т.е. отрицательный результат проверяемого теста.
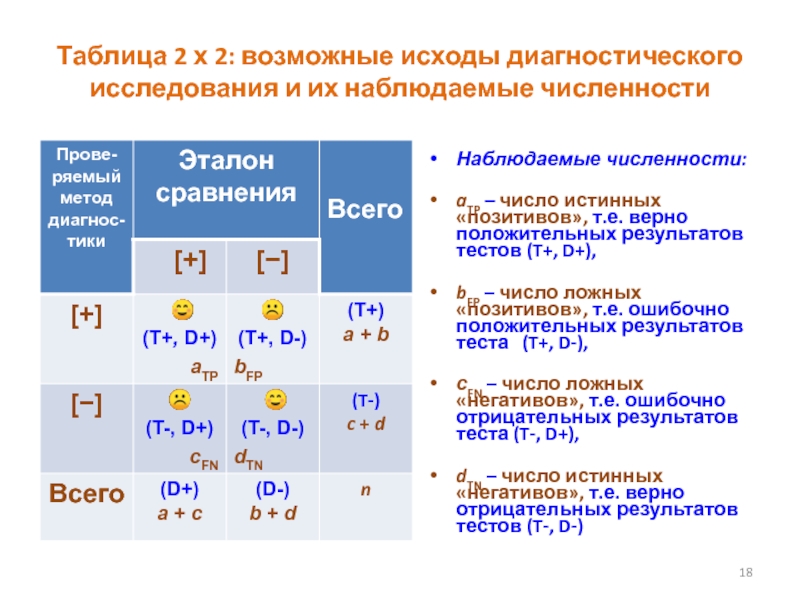
Слайд 18Таблица 2 х 2: возможные исходы диагностического исследования и их
наблюдаемые численности
Наблюдаемые численности:
aTP – число истинных «позитивов», т.е. верно положительных
результатов тестов (T+, D+), bFP – число ложных «позитивов», т.е. ошибочно положительных результатов теста (T+, D-),
сFN – число ложных «негативов», т.е. ошибочно отрицательных результатов теста (T-, D+),
dTN – число истинных «негативов», т.е. верно отрицательных результатов тестов (T-, D-)
Слайд 20Основная логика статистического оценивания: точечные оценки
Обычно вероятности P (или иные
параметры) нам неизвестны.
Мы их оцениваем (благодаря ЗБЧ) по наблюдаемым численностям:
a, b, с и d.Например, точечной оценкой для распространенности болезни по данным одновыборочного исследования P(D+) может служить наблюдаемая частота
f(D+) = (a + c) /n,
т.е. доля больных от общего числа n обследованных.
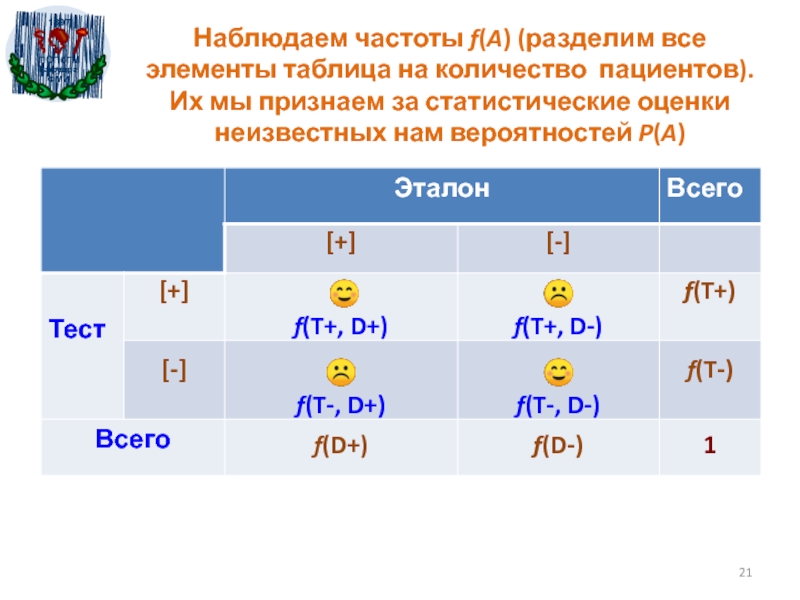
Слайд 21Наблюдаем частоты f(A) (разделим все элементы таблица на количество пациентов).
Их мы признаем за статистические оценки неизвестных нам вероятностей P(A)
Слайд 22Два основных типа статистических оценок
Принципиальной особенностью выборочных данных является их
изменчивость (варьирование).
Поэтому при оценивании на их основе параметров распределения, из
которого они извлечены, нельзя ограничиваться одним числом. Обязательно нужны еще оценки их варьирования. Поэтому различают два типа статистических оценок:
Точечное оценивание – оценка одним числом.
Интервальное оценивание – оценка интервалом.
В статистике для интервального оценивания используются Доверительные Интервалы.
Доверительный интервал — это такой интервал, который содержит (накрывает) неизвестный оцениваемый параметр с заданной вероятностью.
Такая вероятность называется Доверительной Вероятностью или Уровнем Доверия.
Уровень Доверия выбирается исследователем.
Слайд 24Основная логика статистического оценивания: интервальные оценки
Понятно, что если мы многократно
повторим сравнения данного диагностического теста с эталоном сравнения, то наблюдаемые
частоты f(Xi) неизбежно будут варьировать.Поэтому задача математиков – вывести математический закон (вероятностное распределение), которому подчиняется варьирование этой частоты.
Если такой закон найден, то тогда можно получить доверительные интервалы (ДИ) для оценки вероятностей P(Xi) с заданной доверительной вероятностью (1 – α).
Слайд 25Частотнический доверительный интервал и доверительная вероятность
- вероятность того, что истинное,
неизвестное нам значение параметра θunkn расположено внутри данного интервала.
-
вероятность того, что истинное значение оцениваемого параметра θunkn расположено слева от нижней границы этого интервала слева.- вероятность того, что истинное значение оцениваемого параметра θunkn расположено справа от верхней границы этого интервала слева.
Слайд 26Что такое Доверительный Интервал (ДИ)?
100(1 – α)%-й Доверительный Интервал (ДИ)
есть такой интервал, который с заданной доверительной вероятностью
(1 –
α) накрывает искомое оцениваемое значение параметра.
Принципиально важно понимать, что ДИ является случайным.
Это означает, что от опыта к опыту его границы будут колебаться, варьировать.
Слайд 28Точность и надежность статистических оценок
Чем ýже ДИ, тем оценка точнее.
Поэтому
показателем точности интервальной оценки может служить ширина доверительного интервала W
= φU – φL.Чем больше доверительная вероятность (1 – α), тем оценка надежнее.
Однако ДИ с доверительной вероятностью 100% - бессмыслен.
Например, 100%-й ДИ для доли будет содержать все значения в границах от 0 до 1: [0, 1].
Слайд 29ДИ
Итак, например, 99%-й ДИ означает, что если мы многократно повторим
наши наблюдения, то в 99% случаев получаемые интервалы накроют (неизвестное)
значение оцениваемой вероятности P (или иного параметра θ).Но в 1% случаев мы можем «промахнуться»: вычисленный интервал не накроет искомое значение.
И промах этот может случиться как раз с данной конкретной выборкой.
Отсюда мы приходим к выводу о неизбежной необходимости многократно повторять опыты (или наблюдения).
Слайд 30Распознавание и предсказание
Не существует единого количественного показателя, с помощью которого
можно было бы измерить способность диагностического теста распознавать и предсказывать
наличие или отсутствие данной болезни.Показатели качества диагностического теста удобно разделить на
показатели его распознавательной способности и
показатели его предсказательной способности,
Они образуют две пары противоположностей:
показатели и контр-показатели.
Только сопоставляя эти противоположности можно получить их содержательные интерпретации.
Слайд 31Основные вероятностные показатели распознавательной способности диагностического теста
Четыре показателя распознавательной способности
образуют две пары противоположностей:
Чувствительность Se
и контр-чувствительность coSe =
1 – Se. Специфичность Sp
и контр-специфичность coSp = 1 – Sp.
Они являются условными вероятностями
Слайд 32Что такое Чувствительность диагностического теста?
Чувствительность Se (от англ. Sensitivity) есть
вероятность «позитива» у субъекта с болезнью:
P(T+|D+) = P(T+,D+)|[P(D+)]
Она является
вероятностным показателем способности положительных результатов диагностического теста («позитивов») распознавать («чувствовать») наличие болезни.
Слайд 33Что такое Специфичность диагностического теста?
Специфичность Sp (от англ. Specificity) есть
вероятность «негатива» у субъекта без болезни:
P(T-|D-) = P(T-,D-)|[P(D-)]
Она является
вероятностным показателем способности отрицательных результатов диагностического теста («негативов») распознавать отсутствие болезни.
Слайд 34Сводка определений основных показателей распознавательной способности проверяемого диагностического теста (ПДТ)
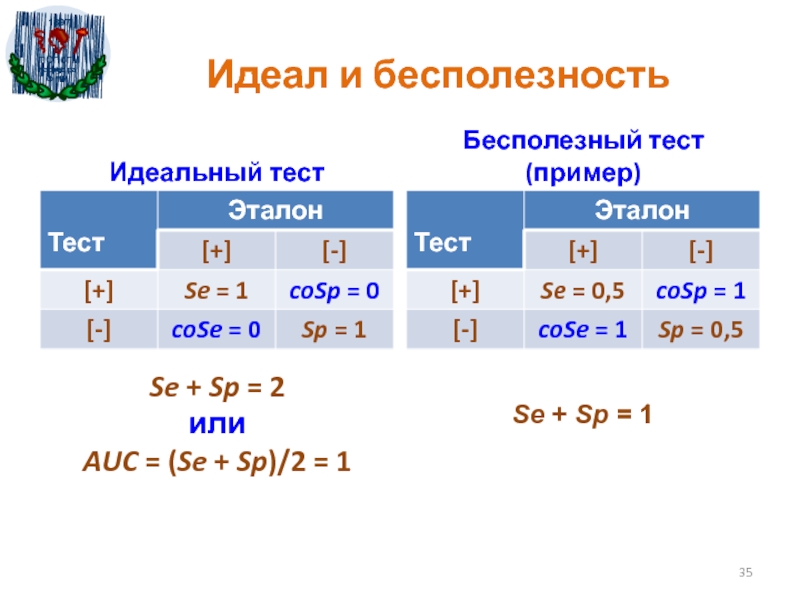
Слайд 35Идеал и бесполезность
Идеальный тест
Бесполезный тест (пример)
Se + Sp = 2
или
AUC
= (Se + Sp)/2 = 1
Se + Sp =
1
Слайд 36Идеальный и бесполезный тесты;
значение AUCuninf = 0,5 – неинформативное
Если
тест идеальный, то
Se = 1 и Sp = 1,
т.
е.Se + Sp = 2 или AUC = (Se + Sp) / 2 = 1
Если
Se + Sp = 1 или AUC = (Se + Sp) / 2 = 0,5,
то тест следует признать бесполезным.
Значение AUCuninf = 0,5 – неинформативное.
Слайд 37ROC-кривые и AUC
Программа: edpsychassociates.com/Software/ROCanalysis.xls
Идеальный тест
Бесполезный тест
Слайд 38Бейзовские точечные оценки показателей распознавательной способности проверяемого диагностического теста (при
равномерном приоре)
Слайд 39Наблюдаемые точечные и интервальные статистические оценки показателей распознавательной способности маммографии
Программа DiagStat.xls
Слайд 40Логика использования доверительных интервалов для оценки статистической значимости полученных результатов
100(1
– α)%-й ДИ является интервальной оценкой истинного, неизвестного нам значения
показателя (параметра) φunkn с заранее выбранной нами доверительной вероятностью 100(1 – α)%.Если 100(1 – α)%-й ДИ не накрывает неинформативное значение оцениваемого показателя (параметра), тогда приходят к выводу, что оцениваемое значение φunkn статистически значимо отличается от неинформативного.
При этом добавляют, что отличие значимо на выбранном уровне значимости α.
Когда же 100(1 – α)%-й ДИ накрывает неинформативное значение оцениваемого показателя, то делают вывод, что оцениваемое значение φunkn статистически не отличается от неинформативного (на данном уровне значимости α).
Слайд 41ROC-кривая и AUC для результатов маммографии
AUC = (Se + Sp)
/ 2 = (0,87 + 0,97) / 2 = 0,92
с
99%-м ДИ от 0,88 до 0,95Компактная запись:
AUC = 0,880,920,95
Полученный 99%-й ДИ [0,88;0,95] не содержит неинформативное значение AUCuninf = 0,5, cледовательно, оцениваемое этим интервалом значение AUCunkn статистически значимо отличается от неинформативного значения 0,5 на уровне значимости α = 0,01.
Слайд 42Статистическая значимость и информативность Se и Sp
Для информативности теста в
целом следует анализировать полусумму Se и Sp. Однако в некоторых
случаях исследователя может интересовать чувствительность или специфичность в отдельности.Например, для скрининга важна чувствительность. Для ROC-анализа, при выборе точки отсечения, необходимо чтобы и Se и Sp были разумно большими.
Для достаточно распространенных заболеваний, будем считать неинформативными для Sp и Se значение 0,5.
В нашем примере маммологического скрининга 99,9%-й ДИ для Se, равный [0,82;0,90], не накрывают неинформативное значения 0,5, значит Se статистически высоко значимо отличается от неинформативного значения 0,5 на уровне на уровне значимости α = 0,001 .
Слайд 45Когда в нашем распоряжении имеются оценки чувствительности и специфичности маммографического
обследования, мы можем сообщить пациентке лишь следующее:
«если у Вас
рак, то вероятность того, что результат Вашего маммографического обследования будет положительным, равна 87%. Если же у Вас нет рака, то вероятность того, что результат Вашего маммографического обследования будет отрицательным, равна 97%».
Слайд 46Предсказательная способность диагностического теста
Получив у данного пациента положительный (или
отрицательный) результат данного диагностического теста, мы более всего заинтересованы получить
ответ на основной прагматический вопрос:Какова вероятность того, что у этого пациента действительно имеется (или действительно отсутствует) данная болезнь?
Статистическая оценка такой вероятности называется предсказательной вероятностью положительного (или отрицательного) результата теста.
Синонимы: предсказательность, прогностичность; предсказательная, прогнозирующая, прогностическая ценность диагностического теста, пост-тестовая вероятность,
По-английски: PPV – Positive Predictive Value (of a test) и NPV – Negative Predictive Value (of a test).
Слайд 47Четыре показателя предсказательной способности образуют две пары противоположностей:
предсказательность «позитивов»
PPV
и их контр-предсказательность coPPV = 1 – PPV
предсказательность «негативов»
NPVи их контр-предсказательность
coNPV = 1 – NPV
Они также являются условными вероятностями
Основные вероятностные показатели предсказательной способности диагностического теста
Слайд 48Определения основных показателей предсказательной способности проверяемого диагностического теста
Слайд 49Вероятностные показатели распознавательной и предсказательной способностей диагностического теста
Слайд 50Что такое Распространенность болезни,
Prev = P(D+)?
Вероятность обнаружить пациента с
данной болезнью в данной популяции: P(D+) называется распространенностью болезни.
Ее
оценкой является доля, f(D+), лиц с данной болезнью в выборке объемом n из данной популяции, выявленных с помощью золотого стандарта.Два варианта оценки распространенности:
Данные демографической (медицинской) статистики.
Общепопуляционное исследование - исследование, в котором из данной популяции отбирают случайным образом большую группу людей (репрезентативную выборку).
Слайд 51Оценка распространенности болезни при одновыборочном исследовании
Вероятность обнаружить пациента с данной
болезнью в данной популяции: P(D+).
В одновыборочном исследовании ее оценкой
является доля лиц с данной болезнью в выборке объемом n из данной популяции: f(D+), выявленных с помощью золотого стандарта.
В одновыборочном исследовании она вычисляется как отношение количества больных (a + c), выявленных с помощью золотого стандарта, в данной выборке, к общему числу обследованных n:
Prev = f(D+) = (a + c)/n
Или
Prev = f(D+) = (a + c +1)/(n + 2)
Слайд 52Бейзовские точечные оценки показателей предсказательной способности ПДТ в одновыборочном исследовании
(при равномерном приоре)
Слайд 53Наблюдаемые значения точечных и интервальных оценок показателей предсказательной способности маммографии
и распространенности рака молочной железы
Программа DiagStat.xls
Слайд 54Статистическая значимость отличия PPV от Prev
В данном случае 99,9%-го ДИ
для PPV [0,13;0,15] не пересекается с 99,9%-м ДИ для Prev
[0,005;0,007], cледовательно, оцениваемое значение PPV статистически значимо отличается от распространенности рака молочной железы в обследованной популяции на уровне значимости α = 0,001.![Статистическая значимость отличия PPV от PrevВ данном случае 99,9%-го ДИ для PPV [0,13;0,15] не пересекается с 99,9%-м](/img/thumbs/84e1156f688ef1801c3c8e0d93acbc4a-800x.jpg "Медицинская биостатистика Лекция 1 Статистика в диагностике Статистическая значимость отличия PPV от PrevВ данном случае 99,9%-го ДИ для")
Слайд 55Идеальный и малопригодный тесты в терминах PPV и NPV
В терминах
предсказательных вероятностей:
Если тест идеальный, то
PPV = 1 и NPV
= 1.Если
PPV ≤ 0,5 и NPV ≤ 0,5,
то тест следует признать практически малопригодным.
Слайд 56Малоинформативные значения показателей предсказательной способности проверяемого диагностического теста (ПДТ)
Слайд 58Компактная форма записи для совместного представления точечных и интервальных оценок
Пример:
Точечная
оценка чувствительности маммографии:
0,87Нижняя граница 99,9%-го доверительного интервала (ДИ): 0,83
Верхняя граница 99,9%-го ДИ: 0,90
Компактная запись:
0,820,870,90
Слайд 59До и после получения позитива
Статистическая оценка вероятности наличия рака молочной
железы до маммографического обследования равна оценке его распространенности:
Prev =
f(D+) = 0,0050,0060,007.После получения позитива 99,9%-й ДИ для предсказательной вероятности наличия у пациентки рака
PPV = f(D+|T+) = 0,120,140,16
не перекрывается с 99,9%-м ДИ для распространенности.
Следовательно, оцениваемое этим интервалом неизвестное значение PPV статистически высоко значимо превышает распространенность болезни.
Слайд 60Контр-прогностичность позитивов
Однако оно статистически значимо МЕНЬШЕ неинформативного значения 0,5, и
мы приходим к выводу о практической непригодности положительных результатов маммографии
для надежного предсказания наличия рака молочной железы.Этот вывод становится очевидным, если обратиться к статистической оценке контр-прогностичности позитивов, которая составила:
coPPV = f(D-|T+) = (1 – PPV) = 0,860,860,88
Таким образом, получается, что наличие позитива свидетельствует не столько о наличии рака молочной железы, сколько о его отсутствии.
Слайд 61До и после получения негатива
Статистическая оценка вероятности отсутствия рака молочной
железы до маммографического обследования равна оценке его контр-распространенности:
coPrev =
f(D-) = 0,9930,9940,995 или 99,41%.После получения негатива оценка предсказательной вероятности отсутствия у пациентки рака статистически значимо повышается и становится равной:
NPV = f(D-|T-) = 0,99890,99920,9994 или 99,92%.
Соответственно, оценка контр-предсказательности негативов получается очень малой:
coNPV = (1 – NPV) = f(D+|T-) = 0,00060,00080,0011 или 0,08%.
Слайд 62Отношения правдоподобий
Между показателями распознавательной и предсказательной способностей ПДТ имеет место
взаимозависимость, которая определяется четырьмя объединяющими их показателями качества диагностического теста,
называемыми отношениями правдоподобий.Они также образуют две взаимно инвертированные пары:
отношение правдоподобий для «позитивов» LR[+] и его инверсия invLR[+] = 1/LR[+],
отношение правдоподобий для «негативов» LR[-] и его инверсия invLR[+] = 1/LR[-].
Слайд 64Идеальный и бесполезный тесты в терминах LR; значение LRuninf =
1 – неинформативное
Если тест идеальный, то
LR[+] = и
LR[-] = .Если
LR[+] ≤ 1 и LR[-] ≤ 1,
то тест следует признать бесполезным.
Значение LRuninf = 1 – неинформативное.
![Идеальный и бесполезный тесты в терминах LR; значение LRuninf = 1 – неинформативноеЕсли тест идеальный, то LR[+]](/img/thumbs/470bfda79a00c1e38f3ffb460049019f-800x.jpg "Медицинская биостатистика Лекция 1 Статистика в диагностике Идеальный и бесполезный тесты в терминах LR; значение LRuninf = 1")
Слайд 65Точечные и интервальные статистические оценки отношений правдоподобий для положительных и
отрицательных результатов маммографии
В данном случае 99,9%-е ДИ для обоих LR
не накрывают неинформативные значения LR[+]uninf = LR[-]uninf = 1. Значит, оцениваемые этими ДИ неизвестные истинные значения обоих LR статистически высоко значимо отличаются от неинформативного значения (на уровне значимости α = 0,001).
Слайд 66Две интерпретации LR
LR[+] показывает, во сколько раз чаще позитивы
будут получаться у субъектов с болезнью, чем у субъектов без
болезни.LR[-] показывает, во сколько раз чаще негативы будут получаться у субъектов без болезни, чем у субъектов с болезнью.
В то же время отношение правдоподобий для позитивов LR[+] показывает, во сколько раз различаются претестовые (априорные) и посттестовые (апостериорные) «одды» (шансы) в пользу наличия болезни против ее отсутствия.
А отношение правдоподобий для негативов LR[-] показывает, во сколько раз различаются претестовые (априорные) и посттестовые (апостериорные) «одды» (шансы) в пользу отсутствия болезни против ее наличия.
![Две интерпретации LR LR[+] показывает, во сколько раз чаще позитивы будут получаться у субъектов с болезнью, чем](/img/thumbs/e6aafa4bc32f28719612d1a587061143-800x.jpg "Медицинская биостатистика Лекция 1 Статистика в диагностике Две интерпретации LR LR[+] показывает, во сколько раз чаще позитивы будут")
Слайд 67Что такое «шансы за/против» («одды») для случайного события?
Два английских слова
chance и odds на русский переводятся фактически одинаково: «шанс» и
«шансы».Это создает трудности в их понимании.
Поэтому здесь для термина odds предлагается использовать уточняющее словосочетание «шансы за/против».
Шансы за/против события A есть отношение вероятности осуществления этого события P(A) к вероятности его неосуществления P(Ā):
O(A) = P(A) / P(Ā) = P(A) / [1 – P(A)]
Слайд 68LR в терминах шансов за/против («оддов»)
LR[+]
есть отношение посттестовых шансов
за/против наличия болезни к претестовым шансам у субъекта с «позитивом».
LR[-]
есть отношение посттестовых шансов за/против отсутствия болезни к претестовым шансам у субъекта с «негативом».
![LR в терминах шансов за/против («оддов»)LR[+] есть отношение посттестовых шансов за/против наличия болезни к претестовым шансам у субъекта](/img/thumbs/220a9e27b548cfb1e2bc5379c3a213ba-800x.jpg "Медицинская биостатистика Лекция 1 Статистика в диагностике LR в терминах шансов за/против («оддов»)LR[+] есть отношение посттестовых шансов за/против")
![Принятые словесные интерпретации для градаций LR[+] и LR[-]](/img/tmb/4/304839/b04c3fd662ebb05d1f51e482931c0c52-800x.jpg "Медицинская биостатистика Лекция 1 Статистика в диагностике Принятые словесные интерпретации для градаций LR[+] и LR[-]")
Слайд 71Сводка основных полученных результатов по статистическим оценкам распознавательной и предсказательной
способностей маммографии для скрининга рака молочной железы и их интерпретация
Слайд 72Полезное правило
Где и когда только возможно, следует визуализировать результаты статистического
анализа, т.е. представлять их наглядно – графически.
Слайд 73График предсказательностей.
Программа DiagStat.xls
Чем более выгнута красная кривая для PPV,
тем лучше способность положительных результатов теста предсказывать наличие болезни.
Чем более
выгнута синяя кривая для (1 – NPV), тем лучше способность отрицательных результатов теста предсказывать отсутствие болезни.
Слайд 74Сравнение графиков предсказательностей с шаблоном
http://en.wikipedia.org/wiki/Pre-_and_post-test_probability
Слайд 75Предсказательно-информативная распространенность заболевания PPVinf
Точечной оценкой предсказательно-информативной распространенности при заданном (фиксированном)
значении планируемой предсказательности позитивов является:
Если мы хотим иметь предсказательность хотя
бы PPVfix = 0,5, то:
Слайд 76Предсказательно-информативные распространенности infPrev для планируемых значений предсказательности planPPV
В группе
риска женщин с распространенностью РМЖ Prev = 25% маммография будет
предсказывать наличие РМЖ с вероятностью PPV = 90%.
Слайд 81Что такое исследование типа
«случаи – контроли»?
При формировании выборок
по схеме «случаи – контроли» случайным образом отбираются две независимые
группы субъектов:- группа субъектов с болезнью – «случаи» и
- группа субъектов без болезни – «контроли»
Такие исследования менее затратны, чем одновыборочные.
Но для них необходимо иметь оценки распространенности заболевания, которые так или иначе получаются на основе одновыборочных иследований.
Слайд 82Целиакия
Целиакия — нарушение пищеварения, которое вызывается некоторыми пищевыми продуктами, содержащими определённые белки —глютен (клейковина) и близкие
к нему белки (авенин, гордеин и др.) в таких злаках, как пшеница, рожь, ячмень и овёс.
У некоторых
субъектов, предрасположенных к целиакии, эти белки приводят к повреждению ворсинок тонкой кишки.Болезнь имеет смешанный аутоиммунный, аллергический, наследственный генез, наследуется по аутосомно-доминантному типу.
Синонимы: болезнь Ги — Гертера — Гейбнера, глютенэнтеропатия, кишечный инфантилизм (англ.: Coeliac disease, non-tropical sprue, c(o)eliac sprue, gluten enteropathy and gluten intolerance).
Слайд 83Вохмянина Н.В. Опыт HLA-генотипирования больных целиакией. Диагностическая значимость HLA-DQ2 и
HLA-DQ8. // Медицинская генетика, 2010. - Том 9, N 7. - С.
33-41.
Слайд 84ROC-кривая и AUC для HLA-гаплотипирования целиакии
AUC = (Se + Sp)
/ 2 = (0,92 + 0,56) / 2 = 0,74
с
99%-м ДИ от 0,68 до 0,80
Компактная запись:
AUC = 0,680,740,80
Слайд 85Предсказательность позитива PPV и негатива NPV в двухвыборочном исcледовании
В
общем виде согласно теореме Байеса (Бейза)
Слайд 86Распространенность целиакии
Долгое время целиакия считалась редким заболеванием с распространенностью от
1 : 10 000 до 1 :1000.
Однако по современным данным
она считается довольно распространенным заболеванием. В США и в Европе (в России в частности) распространенность целиакии варьирует от 1:300 до 1:100, т.е. от 0,3% до 1%.
Средняя распространенность целиакии в мире оценивается как 1 : 184, т.е. 0,54%.
Слайд 87Сравнение диагностической и прогностической способностей маммографии и HLA-гаплотипирования
Мамография и рак
молочной железы
Se = 0,830,870,90
Sp = 0,9670,9680,969
LR[+] = 252729
LR[-] =
0,110,140,17f(D+) = 0,00540,00590,0065
PPV = 0,1260,1390,153
NPV = 0,99890,99920,9994
HLA-гаплотипирование и целиакия
Se = 0,860,920,95
Sp = 0,530,560,58
LR[+] = 1,82,12,3
LR[-] = 0,080,150,26
«Внешние данные»:
f(D+) = 0,0054
Размах: от 0,0033 до 0,010
PPV = 0,0070,0110,18
NPV = 0,99820,99920,9996
![Сравнение диагностической и прогностической способностей маммографии и HLA-гаплотипированияМамография и рак молочной железыSe = 0,830,870,90Sp = 0,9670,9680,969 LR[+]](/img/thumbs/deb8db03cc800f685b2e088a9fe502a9-800x.jpg "Медицинская биостатистика Лекция 1 Статистика в диагностике Сравнение диагностической и прогностической способностей маммографии и HLA-гаплотипированияМамография и рак молочной")
Слайд 88Зависимость предсказательностей PPV и coNPV для HLA-гаплотипирования целиакии от ее распространенности
Prev
Слайд 89Почувствуйте разницу
Прогностичности маммографии при раке молочной железы
Прогностичности HLA-гаплотипирования
Слайд 91Вохмянина Н.В. Опыт HLA-генотипирования больных целиакией. Диагностическая значимость HLA-DQ2 и
HLA-DQ8. // Медицинская генетика, 2010. - Том 9, N 7. - С.
33-41. Mäki M., Mustalahti K., Kokkonen J., Kulmala P., Haapalahti M., Karttunen T., Ilonen J., Laurila K., Dahlbom I., Hansson T., Höpfl P., Knip M. Prevalence of celiac disease among children in Finland . N. Engl. J. Med. – 2003. Vol. 348. – P. 2517-2524.
Слайд 92 Вохмянина Н.В. Опыт HLA-генотипирования больных целиакией. Диагностическая значимость HLA-DQ2 и
HLA-DQ8. // Медицинская генетика, 2010. - Том 9, N 7. - С.
33-41. Mäki M., Mustalahti K., Kokkonen J., Kulmala P., Haapalahti M., Karttunen T., Ilonen J., Laurila K., Dahlbom I., Hansson T., Höpfl P., Knip M. Prevalence of celiac disease among children in Finland . N. Engl. J. Med. – 2003. Vol. 348. – P. 2517-2524.
Слайд 94Lotufo P.A., Chae C.U., Ajani U.A., Hennekens C.H., Manson J.A.E.
Male pattern baldness and coronary heart disease: The Physician's Health
Study // Arch. Intern. Medicine, 2000. – Vol. 160. – P. 165-171. Simon A., Worthen D. M., Mitas J. A.1979. An evaluation of iridology // JAMA, V. 242, N 1, P. 1385‑1389. 13.Алопеция и ИБС
Иридодиагностика и почечная недостаточность
Слайд 95Известно, что евнухи, когда они становятся евнухами в возрасте до
25 лет, не лысеют.
Вряд ли найдется врач, который на
основании этих данных будет рекомендовать молодым людям обзаводиться детьми до 25 лет, а потом становится евнухами для того, чтобы на 2% снизить риск развития у них ИБС. Однако это очень похоже на рекомендации медицинских генетиков, подавляющее большинство которых слишком часто бывают основаны на столь же клинически ничтожных значениях распознавательной и предсказательной способностей генетических маркеров.
Редко значения отношения правдоподобий для позитивов в этих работах превышают значение LR[+] > 2.
Слайд 96Druzhevskaya A.M, Ahmetov I.I., Astratenkova I.V., Rogozkin V.A. 2008. Association
of the ACTN3 R577X polymorphism with power athlete status in
Russians // Eur. J. Appl. Physiol., 2008. – Vol. 103. – P. 631–634. Кундас Л.А., Жур К.В., Бышнев Н.И. и др. Анализ молекулярно-генетических маркеров, ответственных за устойчивость к физическим нагрузкам, у представителей академической гребли // Молекулярная и прикладная генетика: сб. науч. тр. Институт генетики и цитологии НАН Беларуси; (гл. ред. А.В. Кильчевский). 2013. - Минск: ГНУ «Институт генетики и цитологии НАН Беларуси», Т. 14. – C. 101-105.Ген ACTN3 и элитные атлеты
Ген PPARG и элитные гребцы
Слайд 97Mayeux R., Saunders A.M., Shea S., et al. Utility of
the apolipoprotein E genotype in the diagnosis of Alzheimer’s disease
// N. Engl. J. Med., 1998. – Vol. 338. – P. 506-511. Mäki M., Mustalahti K., Kokkonen J., et al. 2003. Prevalence of celiac disease among children in Finland // N. Engl. J. Med, 2003. – Vol. 348. – P. 2517-2524.Ген APOE и болезнь Альцгеймера
Гаплотипы HLA и целиакия
Слайд 98Banks E., Reeves G., Beral V., Bull D., Crossley B.,
Simmonds M., Hilton E., Bailey S., Barrett N., Briers P.,
English R., Jackson A., Kutt E., Lavelle J., Rockall L., Wallis M.G., Wilson M., Patnick J. Influence of personal characteristics of individual women on sensitivity and specificity of mammography in the Million Women Study: cohort study // BMJ, 2004. - Vol. 329. – No. 7464. – P. 477-479. Delaney K.P., Branson B.M., Uniyal A., Kerndt P.R., Keenan P.A., Jafa K., Gardner A.D., Jamieson D.J., Bulterys M. Performance of an oral fluid rapid HIV-1/2 test: experience from four CDC studies // AIDS, 2006. – Vol. 20. – P. 1655–1660.Маммография и рак молочной железы
Экспресс-тест на ВИЧ, OraQuick
