Слайд 1Механика
Кириенко Ольга Ивановна
Доцент, канд. техн. наук
Кафедра ИТ («Информационные технологии»)
Кабинет
Слайд 2Механика
Механика включает в себя три раздела: «Теоретическая механика», «Сопротивление
материалов», «Детали машин».
В разделе «Теоретическая механика» изучаются основные законы движения
твердых тел и их взаимодействие.
В разделе «Сопротивление материалов» изучаются основы прочности материалов и методы расчетов элементов конструкций на прочность, жесткость и устойчивость при действии внешних сил.
В разделе «Детали машин» рассматриваются основы конструирования и расчета деталей и сборочных единиц общего назначения.
Слайд 3
Рекомендуемая литература
1. Тарг С.М. Краткий курс теоретической механики.
– М.: Наука, 2001 (2008).
Александров А.В., Потапов В.Д., Державин Б.П.
Сопротивление материалов. Учебное пособие для вузов. Издание 3.- М.: Высш. шк., 2003.
2. Олофинская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: учеб. пособие / В.П. Олофинская. – 3-е изд., испр. – М.:ФОРУМ, 2012.
Ерохин М.Н. Детали машин и основы конструирования.- М.: «КолосС».- 2004.
Батурин А.Т. Детали машин. Учебник для машиностроительных техникумов. Издание 6-е стереотипное.- М.: «Машиностроение».- 1971.
Березовский Ю.Н. Детали машин для техникумов.- М.: «Маш-ение».-1983.
3. Олофинская В.П. Детали машин. Краткий курс и тестовые задания: учеб. пособие / В.П. Олофинская. - 2-е изд., испр. и доп. – М.:ФОРУМ, 2010.
Слайд 4
Теоретическая механика изучает основные законы движения твердых тел и их
взаимодействие.
Механическим движением называется происходящее с течением времени изменение взаимного положения
материальных тел в пространстве.
Под механическим взаимодействием понимают те действия материальных тел друг на друга, в результате которых происходит изменение движения этих тел или изменение их формы (деформация). За основную меру этих действий принимают величину, называемую силой.
Слайд 53. Введение
Основной задачей теоретической механики является изучение движения материальных тел
под действием сил.
По характеру рассматриваемых задач механику разделяют на
статику, кинематику и динамику.
В статике излагается учение о силах и условиях равновесия материальных тел под действием сил.
В кинематике – общие геометрические свойства движения тел.
В динамике изучается движение материальных тел под действием сил.
В классической механике все вводимые исходные положения и понятия являются научными моделями.
ТМ, в отличие от физики, изучает з-ны движения абстрактных абсолютно твердых тел, здесь материалы, форма тел существенного значения не имеют. При движении абсолютно твердое тело не деформируется и не разрушается.
Слайд 64. Введение
Основные абстрактные модели реальных тел:
материальная точка – имеет массу,
но не имеет размеров;
абсолютно твёрдое тело – объём конечных
размеров, сплошь заполненный веществом, причём расстояния между любыми двумя точками не изменяются во время движения;
Из них – системы:
- система свободных материальных точек; если при движении системы материальных точек расстояние между точками остаются постоянными, то такая система материальных точек называется неизменяемой системой;
- системы со связями.
«Вырожденные» модели:
- бесконечно тонкие стержни;
- бесконечно тонкие пластины;
- невесомые стержни и нити, связывающие между собой материальные точки, и т.д.
Слайд 76. Введение.
Положение объекта относительно другого физического тела (например, Земли) определяется
при помощи выбранной системы координат
Система отсчета. Cистема декартовых прямоугольных
координат.
Инерциальная система отсчёта – такая, собственное движение которой не может быть обнаружено никаким механическим опытом.
Все системы отсчёта, движущиеся относительно исходной прямолинейно и равномерно, будут инерциальными. Это позволяет ввести единую декартовую систему координат.
Условное соглашение – берут правую систему координат (рис. 1).
Время – абсолютно, единое для всех систем отсчёта, т. е. начальный момент – произволен.
Состояние движения тел в момент времени t определяется координатами и скоростями точек в этот момент.
Слайд 87. Статика
Статикой называется часть механики, где изучаются условия, которым должны
удовлетворять силы, действующие на систему материальных точек, для того чтобы
система находилась в равновесии.
Сила – это мера механического взаимодействия материальных тел между собой, способного вызвать движение тел из состояния покоя или изменить существующее движение тел.
Совокупность сил, приложенных к данному твердому телу, называется системой сил.
Слайд 98. Статика.
Система материальных точек находится в равновесии, если, будучи в
покое, она не получает никакого движения от сил, на неё
действующих. В этом случае система сил, приложенных к ней, называется уравновешивающей, а силы в системе взаимно уравновешенными.
Из повседневного опыта: силы имеют векторный характер, то есть величину (модуль), направление, линию действия, точку приложения.
Условие равновесия сил, действующих на твёрдое тело, сводится к свойствам систем векторов.
Если в характеристике величины направление не имеет значение, то эта величина называется скалярной (объем тела, температура).
Слайд 109. Статика. Аксиомы.
Принципы построения курса теоретической механики:
1)
в основе – система аксиом (на основе опыта, наблюдений -
сформулировали Галилей и Ньютон);
2) далее – законы внутренней логики (относительная независимость теории).
Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами. Аксиомы, устанавливающие общие закономерности механического движения, созданы в результате обобщения человеческого опыта.
Аксиома 1. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно.
Аксиома 2. Две силы, приложенные к твёрдому телу, взаимно уравновешиваются тогда и только тогда, когда они равны по величине, направлены в противоположные стороны и лежат на одной прямой.
Аксиома 3. Действие на твёрдое тело системы сил не изменится, если добавить к этой системе или отбросить от неё две силы, равные по величине, направленные в противоположные стороны и лежащие на одной прямой.
Слайд 1110. Статика.
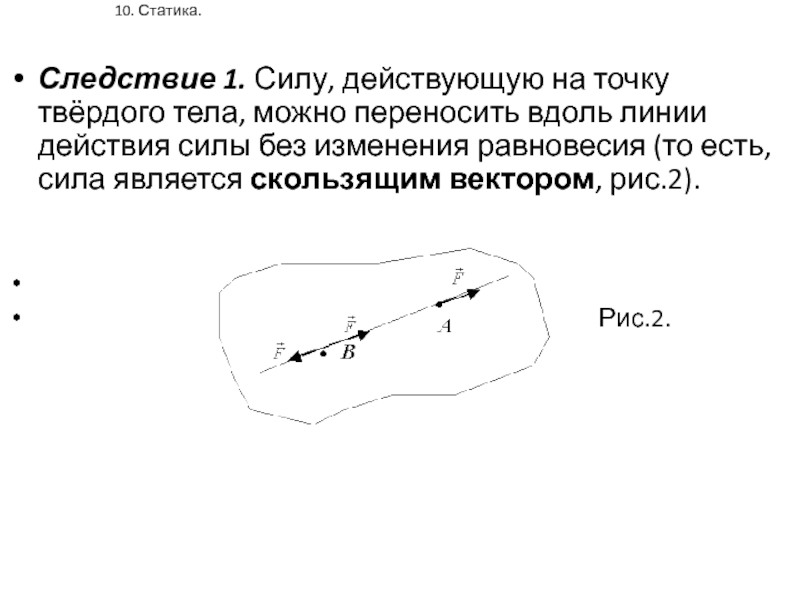
Следствие 1. Силу, действующую на точку твёрдого тела, можно
переносить вдоль линии действия силы без изменения равновесия (то есть,
сила является скользящим вектором, рис.2).
Рис.2.
Слайд 1211. Статика. Аксиомы.
Аксиома 4. Действие на точку твёрдого тела нескольких
сил равносильно действию одной равнодействующей силы, строящейся по правилу сложения
векторов (рис.4).
Рис. 4.
Следствие. Силы, приложенные к точке твердого тела, складываются по правилу параллелограмма.
Слайд 1313. Статика. Аксиомы.
Аксиома 5. Если деформируемое (не абсолютно твердое) тело,
находящееся под действием сил в состоянии равновесия, станет абсолютно твердым
(отвердеет), то его равновесие не нарушится (принцип отвердевания).
Из этого закона следует, что условия, которым должны удовлетворять при равновесии силы, приложенные к абсолютно твердому телу, необходимо соблюдать и при равновесии тела деформируемого. Поэтому этот закон устанавливает связь между статикой абсолютно твердого тела и статикой деформируемых тел.
Слайд 1414. Статика. Аксиомы.
Действие одного тела на другое никогда не может
быть односторонним: мы всегда наблюдаем взаимодействие материальных тел.
Две категории
сил:
1) Активные - создают или способны создать движение твёрдого тела. Например, сила тяжести.
2) Пассивные – не создающие движения, но ограничивающие перемещения твёрдого тела, препятствующие перемещениям. Например, сила натяжения нерастяжимой нити (рис.7).
Рис.7.
Слайд 1515. Статика. Аксиомы.
Аксиома 6. Действие одного тела
на второе равно и противоположно действию этого второго тела на
первое (действие равно противодействию). Например, Земля и Луна.
Важно - действие и противодействие представляют собой две силы, приложенные к двум разным телам. Поэтому нельзя сказать, что эти две силы уравновешиваются.
Тело, перемещениям которого в пространстве препятствуют другие тела, скрепленные или соприкасающиеся с ним, называется несвободным, или связанным. Все то, что ограничивает перемещения данного тела в пространстве, называется связью.
Силы, обусловленные связями и препятствующие перемещениям, называются силами реакций связи или просто реакцией связи. Направлена реакция связи всегда с той стороны, куда связь не дает перемещаться телу.
Принцип освобождения от связей.
Слайд 1616. Статика. Аксиомы.
Аксиома 7. Связи, наложенные на систему материальных точек,
можно заменить силами реакций, действие которых эквивалентно действию связей.
Типы связей:
1.
Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
2. Гибкая связь (нить, веревка, трос, цепь) – подвешен груз. Реакция направлена вдоль нити от тела, нить растянута.
3. Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня.
Слайд 17 Связи
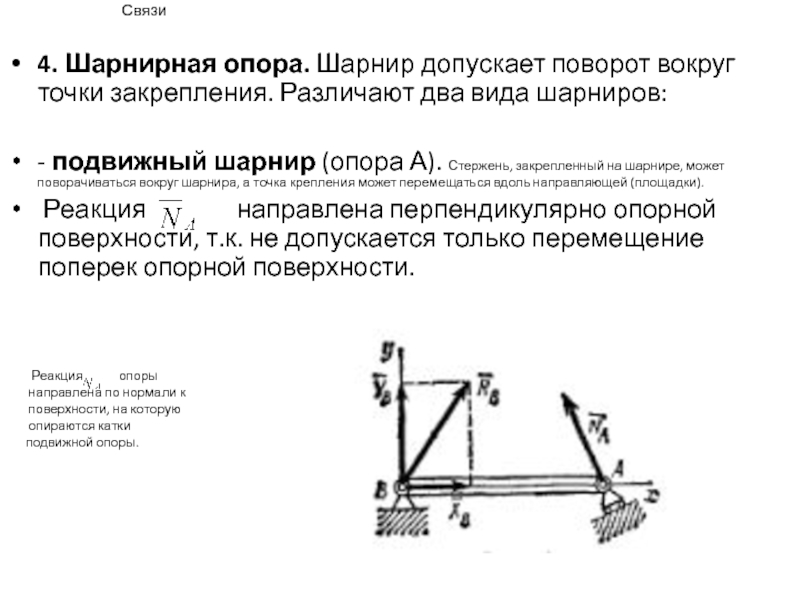
4. Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления.
Различают два вида шарниров:
- подвижный шарнир (опора А). Стержень,
закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки).
Реакция направлена перпендикулярно опорной поверхности, т.к. не допускается только перемещение поперек опорной поверхности.
Реакция опоры
направлена по нормали к
поверхности, на которую
опираются катки
подвижной опоры.
Слайд 18Связи
- неподвижный шарнир (опора В).
Стержень может свободно поворачиваться вокруг
оси шарнира. Реакция опоры проходит через
ось шарнира, но неизвестна по направлению.
Реакцию разлагают на составляющие
и по направлению
координатных осей. Реакция по модулю
определится:
Способ закрепления применяется для того, чтобы исключить возможные напряжения от действия температуры или изгиба.
Слайд 19Связи
5. Защемление , или «заделка».
Любые перемещения точки крепления невозможны.
Под действием
внешних сил в опоре возникают реактивная сила и реактивных момент,
препятствующий повороту.
Слайд 20 Статика. Система сходящихся сил.
1. Определение равнодействующей геометрическим способом
А.
Сложение сил.
Система сил, линии действия которых пересекаются в одной точке,
называется сходящейся.
Рис. 8. Следствие 2 и 3 аксиом. 4-я аксиома. Рис. 9.
Плоская задача. Геометрическая сумма двух сил находится по правилу параллелограмма (рис. 9).
Слайд 2118. Статика.
Объемная задача. Геометрическая сумма трех сил , не
лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих
силах (рис. 10).
Рис. 10. Рис.11.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) не изменится.
Такой способ получения равнодействующей называется геометрическим.
Т.обр., система сходящихся сил имеет равнодействующую, равную геометрической сумме этих сил и приложенную в точке пересечения их линий действия (рис. 11).
Слайд 2219. Статика.
Б. Разложение сил. Способом разложения удобно пользоваться при определении
сил давления тела на связи и реакции связей.
А) разложение силы
по двум заданным направлениям.
В этом случае сила будет являться диагональю параллелограмма, а стороны параллельны заданным направлениям (рис.9).
Б) разложение силы по трем заданным направлениям.
В этом случае, если заданные направления не лежат в одной плоскости, задача сводится к построению параллелепипеда, диагональю которого и будет являться изображением данной силы, а его ребра будут параллельны заданным направлениям.
Рис.
Рис.9. Рис.10.
Слайд 2321. Статика.
2. Определение равнодействующей аналитическим способом
Аналитический способ сложения
сил. Из аналитической геометрии: Проекция вектора суммы на какую-нибудь
ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Т.е., если , то = , = , .
Зная находим:
; ; ;
. Если силы расположены в одной плоскости, формулы принимают вид:
Слайд 2423. Статика. Момент силы .
Момент силы относительно центра
Под действием силы тело
может совершать вращательное движение вокруг некоторой точки. Момент силы характеризует вращательный эффект.
Центром момента называют точку, относительно которой берется момент. Момент относительно центра – момент относительно этой точки.
В точке А к телу приложена сила . Из центра О опустим перпендикуляр на линию действия силы, его длина - плечо силы относительно центра О. Момент силы относительно центра О определяется модулем момента, равным Fh; положением в пространстве плоскости ОАВ («плоскость поворота); направлением поворота в этой плоскости. Значит, момент силы – векторная величина.
Рис.16
Слайд 2525. Статика. Пара сил. Момент пары сил
Система двух параллельных сил,
равных по величине и направленных в противоположные стороны, называется парой
сил (рис.17).
Рис.17.
.
Плоскость действия пары сил - плоскость, проходящую через линии действия сил.
Плечо пары сил – расстояние d между линиями действия сил пары.
Тело под действием пары сил совершает вращательное движение, следовательно, можно говорить о моменте пары. Его характеризует: модуль, равный Fd; положение плоскости действия пары; направление поворота пары в этой плоскости. Т.о., момент пары сил – векторная величина.
Слайд 26 Статика. Пара сил. Момент пары сил
Момент пары численно равен
произведению модуля силы на плечо пары Fd.
Момент считается положительным,
если пара вращает тело против хода часовой стрелки.
Слайд 2728. Статика.
Теорема Пуансо о параллельном переносе силы:
Силу можно перенести параллельно
линии ее действия, при этом нужно добавить пару сил с
моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.
Рис.21.
На тело в точке А действует сила , прикладываем в точке В
две уравновешенные силы = и = - . Система
трех сил представляет собой силу и пару сил с моментом .
Слайд 2829. Статика.
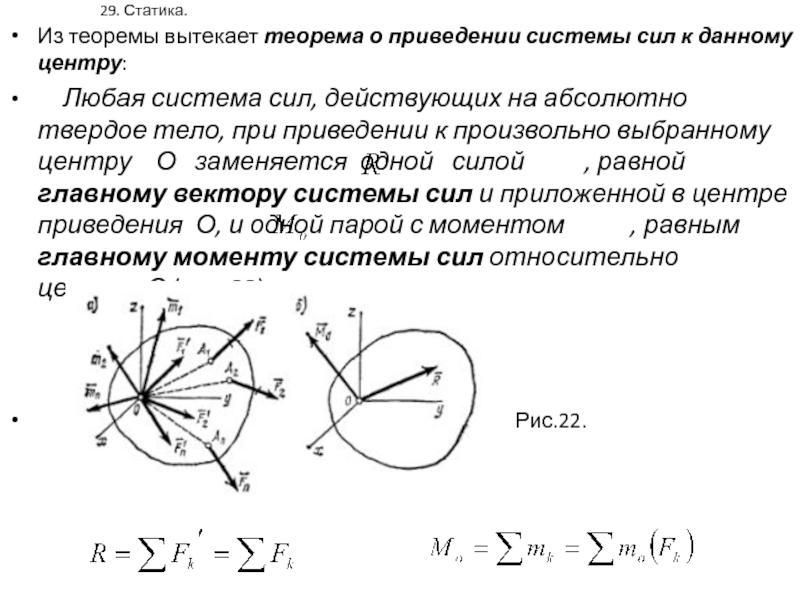
Из теоремы вытекает теорема о приведении системы сил к
данному центру:
Любая система сил, действующих на абсолютно
твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой , равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом , равным главному моменту системы сил относительно центра О (рис.22).
Рис.22.
Слайд 2930. Статика. Теорема о приведении системы сил к данному центру.
Для равновесия любой системы сил необходимо и достаточно, чтобы главный
вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т.е.
.
Слайд 3044. Статика. Главный вектор и главный момент пространственной системы сил.
Главный
вектор и главный момент пространственной системы сил.
Значения главного вектора
и главного момента системы сил определяются равенствами:
.
Проекции главного вектора на оси x,y,z :
.
Проекции главного момента :
.
Слайд 3145. Статика. Равновесие пространственной системы.
Равновесие произвольной пространственной системы сил
Условия равновесия
любой системы сил:
Но векторы и равны нулю тогда, когда проекции главного вектора и главного момента на оси x, y, z равны нулю: ;
, или
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.
Если на тело кроме сил действует еще пара, заданная ее моментом:
Слайд 32Кинематика
Кинематика точки
Кинематика – раздел механики, в котором изучаются геометрические
свойства движения тел. При этом не учитываются масса тел и
силы, которые действуют на них.
Все величины в кинематике рассматриваются как изменяющиеся с течением времени, т.е. как функции времени.
Слайд 332. Кинематика.
Векторный способ задания движения точки.
Положение точки М задается
ее радиусом-вектором , проведенным
из начала координат О в точку М (рис.37).
Рис.37.
При движении точки М вектор рассматривается как переменный вектор (вектор-функция), зависящий от аргумента t:
- уравнение движения или закон движения точки в векторной форме.
В прямоугольных декартовых координатах проекции вектора на оси x, y, z (рис.37): .
Слайд 343. Кинематика.
Координатный способ задания движения точки.
Положение точки можно задать ее
координатами x, y, z, изменяющимися с течением времени.
; ;
- уравнения движения точки или закон движения точки.
Из этих уравнений, исключая время t, можно найти уравнения траектории движения точки.
Слайд 354. Кинематика.
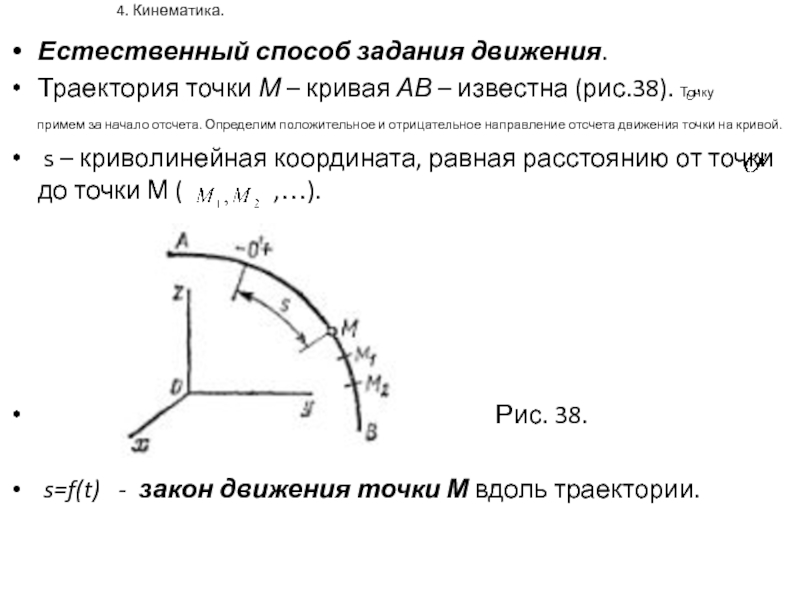
Естественный способ задания движения.
Траектория точки М – кривая АВ
– известна (рис.38). Точку примем
за начало отсчета. Определим положительное и отрицательное направление отсчета движения точки на кривой.
s – криволинейная координата, равная расстоянию от точки до точки М ( ,…).
Рис. 38.
s=f(t) - закон движения точки М вдоль траектории.
Слайд 365. Кинематика.
Вектор скорости точки
Векторная величина, характеризующая в данный момент быстроту
и направление движения по траектории, называется скоростью.
Рис.39.
Перемещение точки за промежуток времени определяется вектором - вектором перемещения точки.
, или .
Средняя по модулю и направлению скорость точки за промежуток времени определяется : .
Направление вектора совпадает с направлением
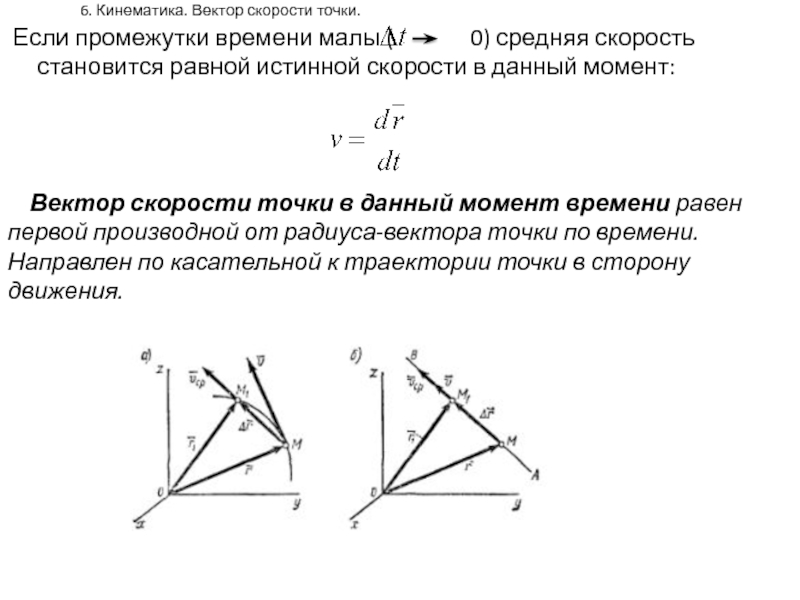
Слайд 376. Кинематика. Вектор скорости точки.
Если промежутки времени малы (
0) средняя скорость становится
равной истинной скорости в данный момент:
Вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени. Направлен по касательной к траектории точки в сторону движения.
Слайд 387. Кинематика.
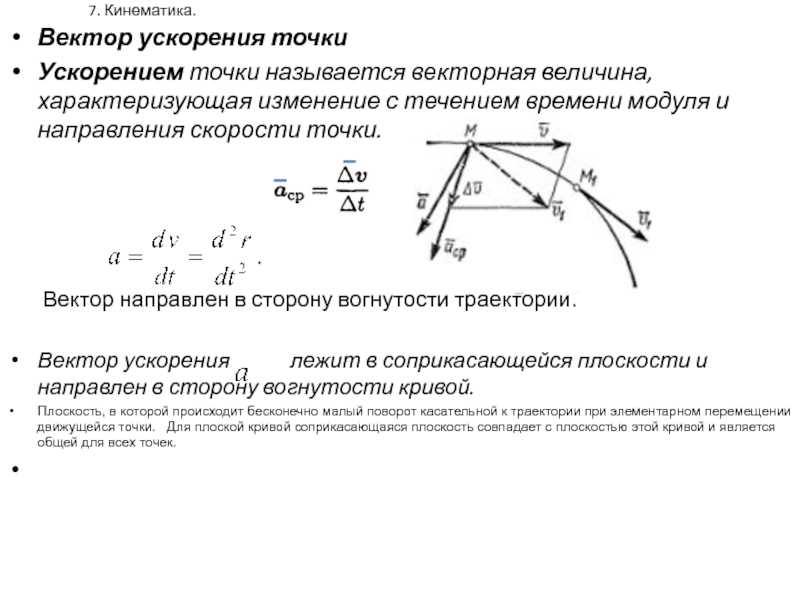
Вектор ускорения точки
Ускорением точки называется векторная величина, характеризующая
изменение с течением времени модуля и направления скорости точки.
Вектор направлен в сторону вогнутости траектории.
Вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
Плоскость, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Для плоской кривой соприкасающаяся плоскость совпадает с плоскостью этой кривой и является общей для всех точек.
Слайд 398. Кинематика.
Скорость и ускорение точки при координатном способе задания движения
Воспользуемся
теоремой: проекция производной от вектора на ось, неподвижную в данной
системе отсчета, равна производной от проекций дифференцируемого вектора на ту же ось.
1. Скорость точки.
Учитывая, что , найдем:
или , ,
Модуль и направление скорости (углы , которые вектор
образует с координатными осями):
, , .
,
Слайд 409. Кинематика.
2. Ускорение точки.
Вектор ускорения:
Отсюда: , , ,
или , , .
Проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени.
Модуль и направление ускорения ( - углы, которые вектор ускорения образует с координатными осями):
;
; ; .
Слайд 4110. Кинематика.
Скорость и ускорение точки при естественном задания движения
Даны траектория
точки и закон движения точки вдоль траектории s=f(t).
Значения векторов
и определяют по их проекциям на подвижные оси , которые движутся вместе с точкой М и называются осями естественного трехгранника, или скоростными осями.
Рис.41.
Направление осей: ось - по касательной к траектории в сторону положительного отсчета расстояния s, ось Мn – по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории, ось Mb – перпендикулярно к осям и Mn так, чтобы она образовала с ними правую систему осей. Нормаль Mn - главная нормаль, нормаль Mb – бинормаль.
Плоскость, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки
Слайд 4211. Кинематика. Скорость и ускорение точки при естественном задании движения.
Поскольку
вектор скорости точки совпадает с осью
, то величина скорости определяется проекцией вектора на эту ось с учетом знака . Знак принято опускать и называть v числовым (алгебраическим) значением скорости.
Числовое значение скорости точки в данный момент времени равно первой производной от расстояния (криволинейной координаты) s этой точки по времени.
Величина v определяет и модуль скорости, и ее направление – по знаку модуля.
Слайд 4312. Кинематика.
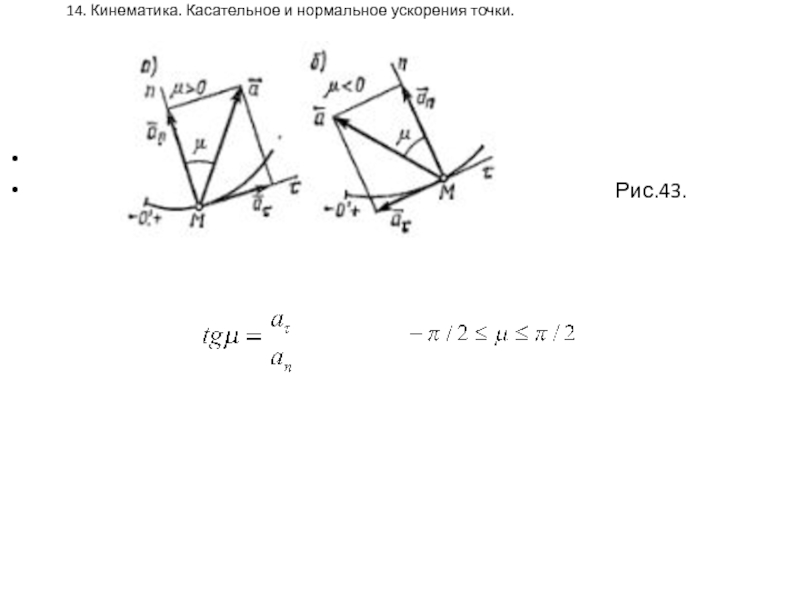
Касательное и нормальное ускорение точки
Проекции вектора
на оси
, Mn, Mb: ,
, ,
где .
Рис.42.
Касательное ускорение характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении движения тела направление совпадает с направлением вектора скорости, а при замедлении – противоположно направлению.
Слайд 4413. Кинематика. Касательное и нормальное ускорения точки
Нормальное
ускорение характеризует изменение скорости по
направлению и определяется:
,
где ᵨ - радиус кривизны траектории в данный момент времени.
Нормальное ускорение всегда направлено перпендикулярно скорости к центру дуги.
Значение полного ускорения :
Слайд 4514. Кинематика. Касательное и нормальное ускорения точки.
Слайд 4615. Кинематика.
Частные случаи движения точки.
1. Прямолинейное движение.
,
, .
Касательное ускорение характеризует изменение числового значения скорости.
2.Равномерное криволинейное движение.
V=сonst, , .
Вектор направлен по нормали к траектории точки.
Нормальное ускорение характеризует изменение скорости по направлению.
Закон равномерного криволинейного движения:
, , , , .
При s=vt, v=s/t.
,
Слайд 4716. Кинематика. Частные случаи движения точки.
3.Равномерное прямолинейное движение.
, . Ускорение точки равно нулю только при равномерном прямолинейном движении.
4.Равнопеременное криволинейное движение.
.
При t=0 , .
, . Интегрируем: . Или
.
Интегрируем: - закон равнопеременного криволинейного движения точки.
Слайд 4822. Кинематика.
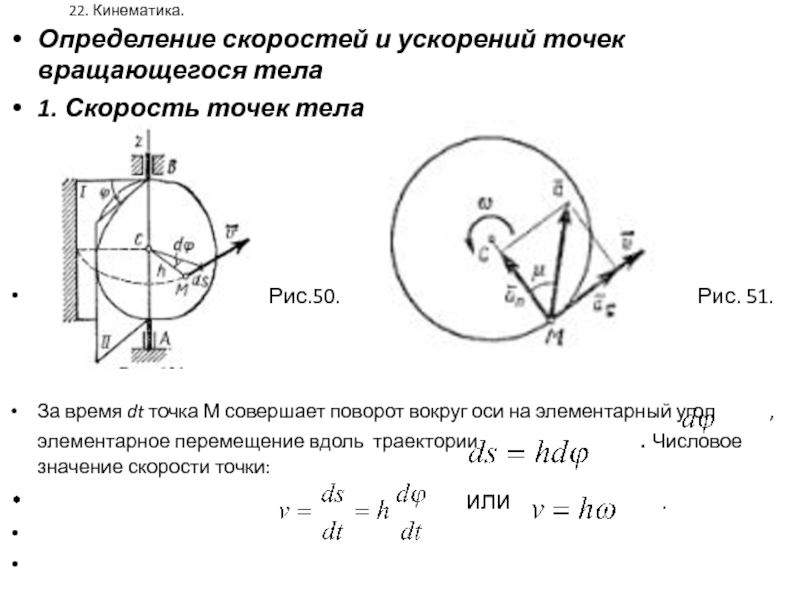
Определение скоростей и ускорений точек вращающегося тела
1. Скорость точек
тела
Рис.50. Рис. 51.
За время dt точка М совершает поворот вокруг оси на элементарный угол , элементарное перемещение вдоль траектории . Числовое значение скорости точки:
или .
Слайд 4924. кинематика. Вращательное движение твердого тела.
2.Ускорение точек тела.
Воспользуемся формулами:
, , .
Тогда, , .
Или , .
Полное ускорение или .
Слайд 5028. Кинематика. Плоскопараллельное движение.
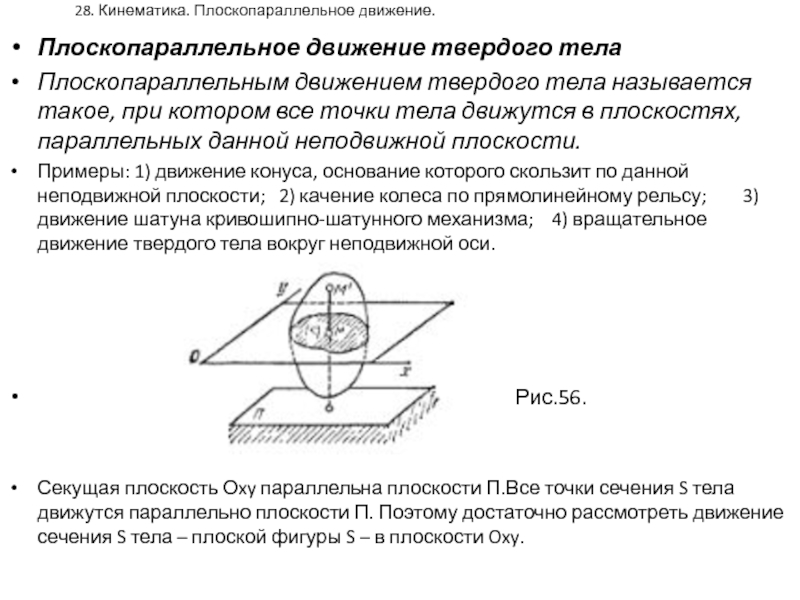
Плоскопараллельное движение твердого тела
Плоскопараллельным движением твердого тела
называется такое, при котором все точки тела движутся в плоскостях,
параллельных данной неподвижной плоскости.
Примеры: 1) движение конуса, основание которого скользит по данной неподвижной плоскости; 2) качение колеса по прямолинейному рельсу; 3) движение шатуна кривошипно-шатунного механизма; 4) вращательное движение твердого тела вокруг неподвижной оси.
Рис.56.
Секущая плоскость Оxy параллельна плоскости П.Все точки сечения S тела движутся параллельно плоскости П. Поэтому достаточно рассмотреть движение сечения S тела – плоской фигуры S – в плоскости Oxy.
Слайд 5129. Кинематика. Плоскопараллельное движение твердого тела.
На плоскости сечения S проведем
отрезок АВ, который и будет определять положение плоской фигуры S.
Положение отрезка определяется координатами ,
и углом (с осью x). Точку А назовем полюсом.
Рис. 57.
, , - уравнения плоскопараллельного движения твердого тела.
Первые два уравнения – уравнения поступательного движения. Третье уравнение определяет движение, которое совершила бы фигура S при неподвижном полюсе А. Следовательно
, Движение плоской фигуры в общем случае можно разложить на два движения: 1) поступательное движение со скоростью, равной скорости произвольно выбранной точки фигуры (полюса); 2) вращательное движение вокруг этой точки.
Слайд 531. Динамика.
Динамика устанавливает и изучает связь между движением материальных
тел и действующими на них cилами.
В динамике решают две задачи:
-
определяют параметры движения по заданным силам;
- определяют силы, действующие на тело, по заданным параметрам движения.
В основе классической динамики лежат законы.
Слайд 542. Динамика.
Первый закон (з-н инерции). Если на материальную точку не
действуют никакие силы, то эта точка или находится в покое,
или движется прямолинейно и равномерно.
Если =0, то =const. В частности =0.
Свойство м. т. сохранять свою скорость неизменной как по модулю, так и по направлению, в частности - состояние покоя, называется инертностью или инерцией.
Всякое тело (точка) обладает инертностью. Мерой ее является масса тела.
Массой называют количества вещества в объеме тела. Единица измерения массы – кг.
Слайд 553. Динамика.
Второй закон (з-н зависимости между силой и количеством движения)
– основной закон динамики.
Модуль силы, действующей на материальную точку, равен
произведению массы точки на модуль ее ускорения, а направление силы совпадает с направлением ускорения.
Векторное уравнение: .
Из закона следует, что при одном и том же ускорении модуль силы пропорционален массе точки, т.е. чтобы сообщить точке данное ускорение, к ней нужно приложить тем большую силу, чем больше ее масса.
Мерой инертности точки является ее масса.
При действии на точку нескольких сил:
или .
В дифференциальной форме:
Слайд 564. Динамика.
Третий закон (з-н равенства действия и противодействия).
Силы взаимодействия двух
тел равны по величине и направлены по одной прямой в
противоположные стороны.
Слайд 575. Динамика.
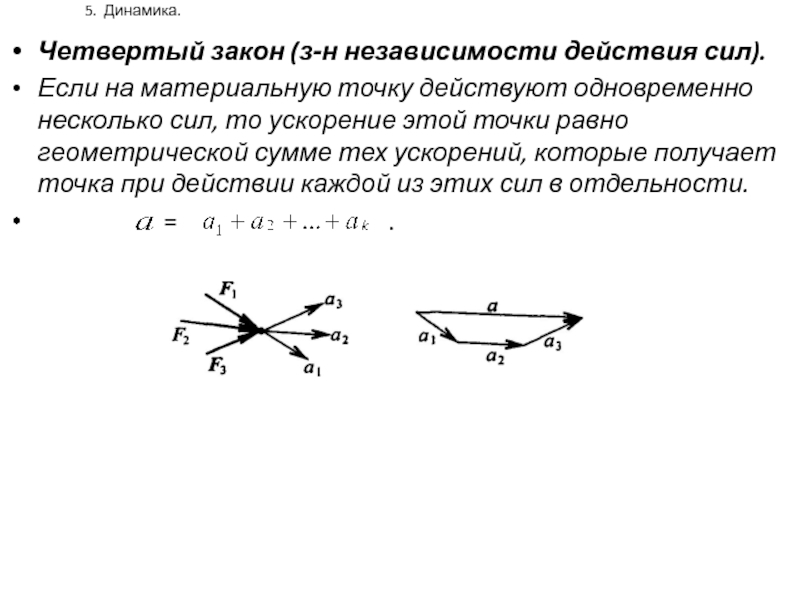
Четвертый закон (з-н независимости действия сил).
Если на материальную точку
действуют одновременно несколько сил, то ускорение этой точки равно геометрической
сумме тех ускорений, которые получает точка при действии каждой из этих сил в отдельности.
= .