Методы обработки изображений на основе математической морфологии

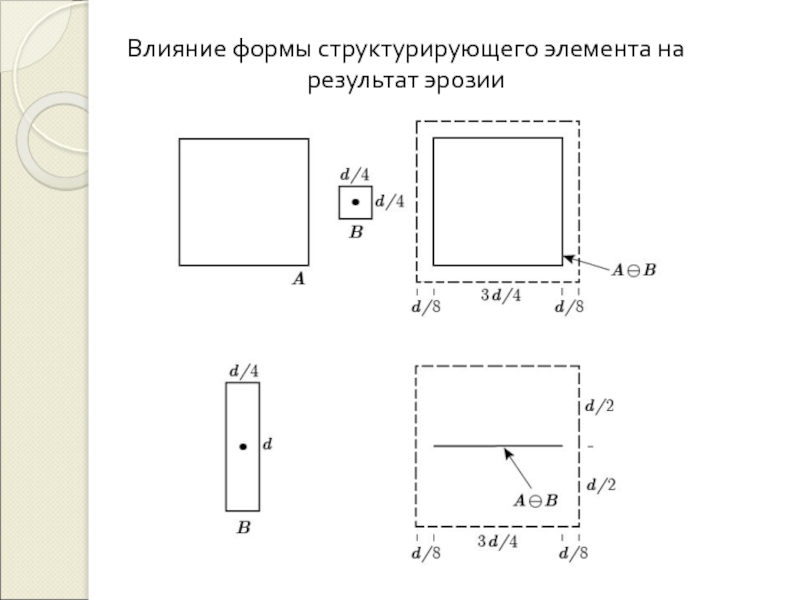
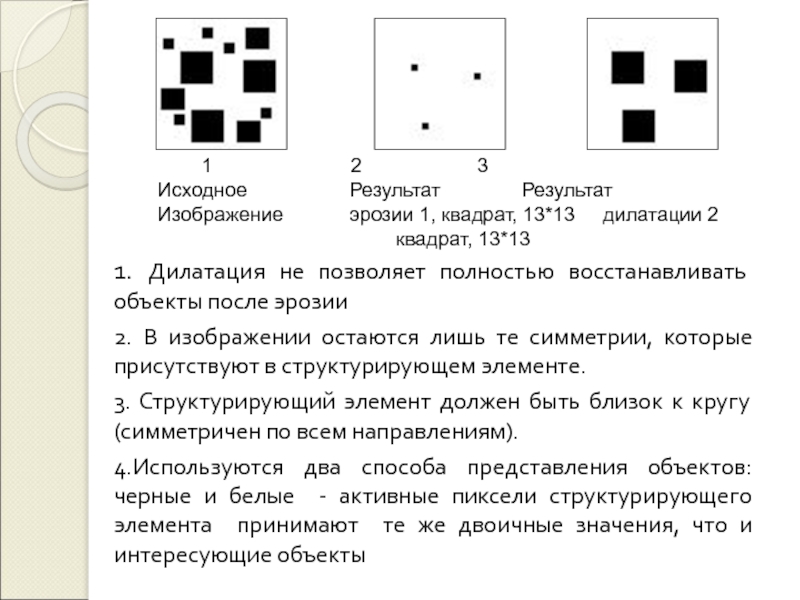
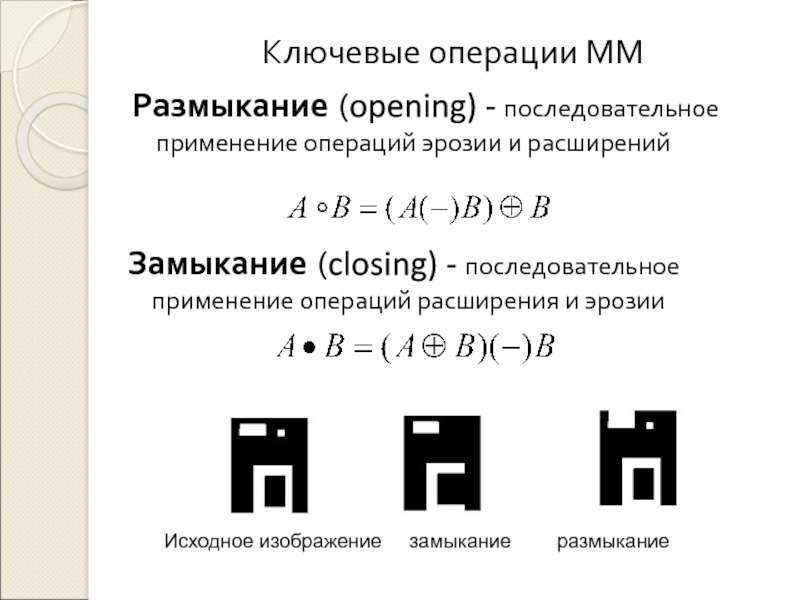
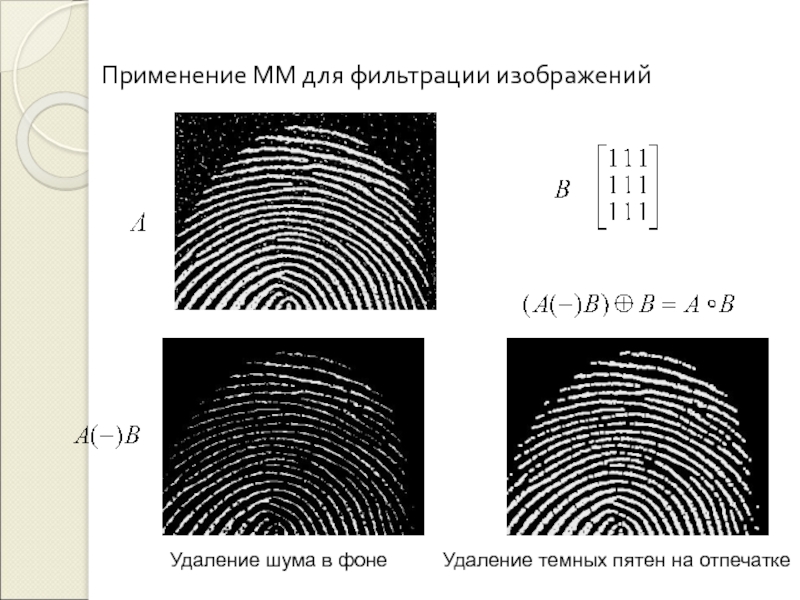
и анализа цифровых изображений / Тузиков А.В., Шейнин С.А., Жук

Ж. Серра и Ж. Матерон - начало 1970-х годов

Гонсалес Р., Вудс Р. Цифровая обработка изображений. – М: Техносфера, 2005. – 1072с. стр. 747-811

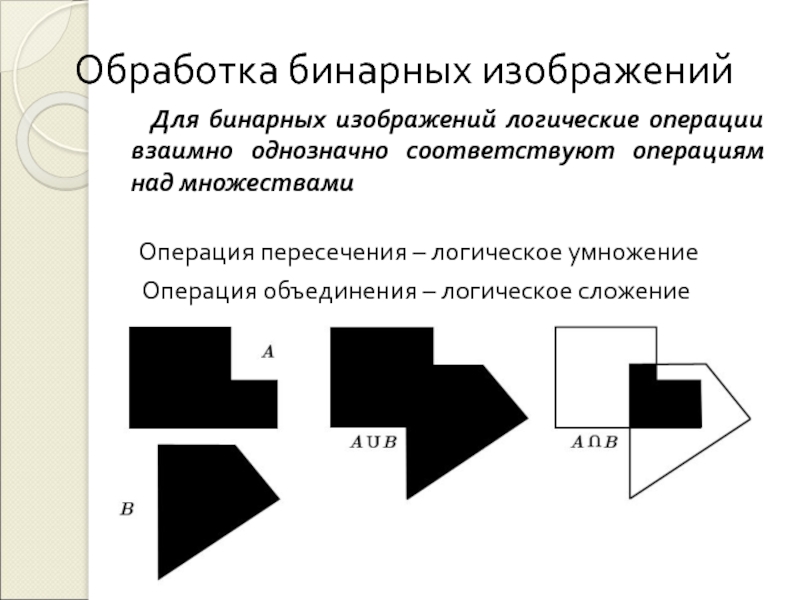
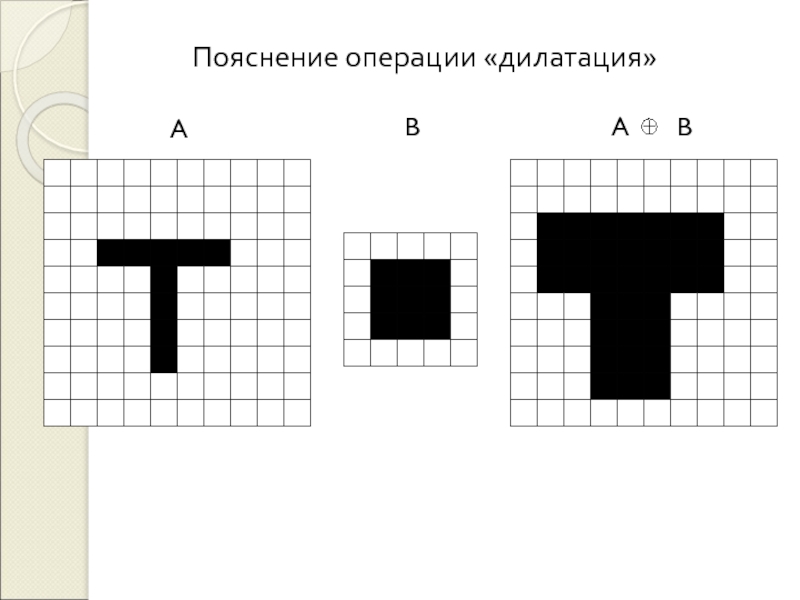
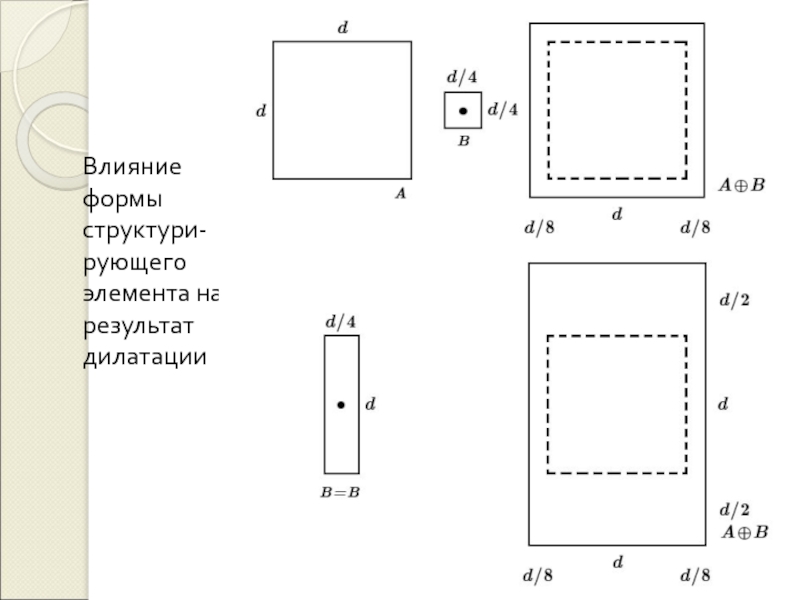
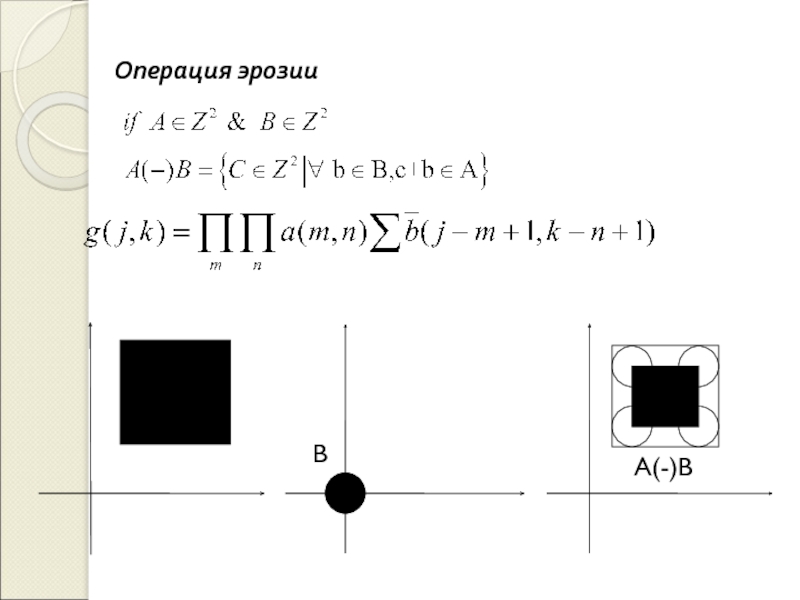
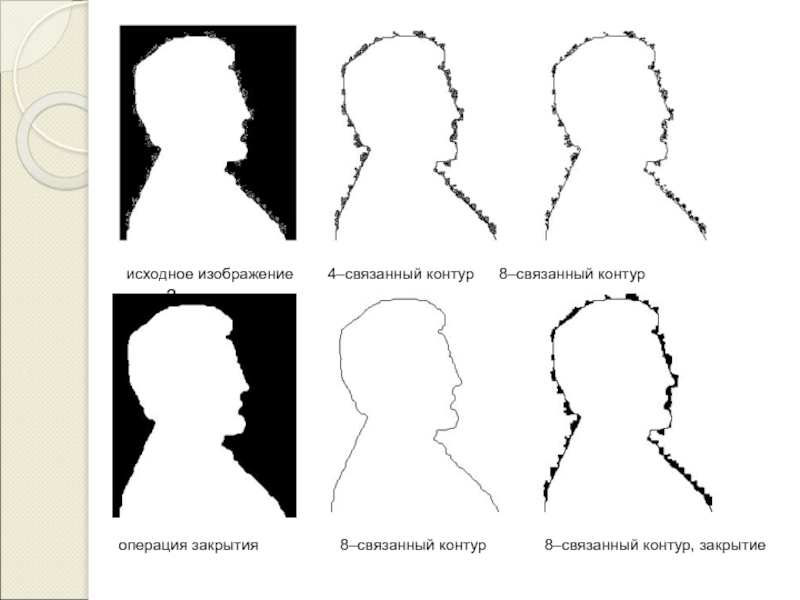
Методы обработки изображений на основе математической морфологии

Абламейко С.В., Лагуновский Д.М. Обработка изображений: технология, методы применение. - Минск: Институт технической кибернетики НАН Беларуси, 1999.-300с. стр. 84-86

(mathematical morphology)

компонент изображения, используемых при его представлении и описании:
границ, заданных областей,

Математическая морфология (ММ)- использует язык теории множеств

Множества в ММ -объекты на изображениях

Основные операции ММ
наращение (расширение, дилатация) (dilation)
эрозия (erosion) 

взаимно однозначно соответствуют операциям над множествами
Операция пересечения –

простой формы (структурирующий элемент-structuring element)
Операция расширения

изображении остаются лишь те симметрии, которые присутствуют в структурирующем элементе.

1 2 3
Исходное Результат Результат
Изображение эрозии 1, квадрат, 13*13 дилатации 2
квадрат, 13*13

расширений


Замыкание (closing) - последовательное применение операций расширения и эрозии

Исходное изображение замыкание размыкание

темных пятен на отпечатке

полос отпечатков
Исходное изображение

контур 3
операция закрытия

b
Примитив b скользит по f
Результат дилатации
Графическое пояснение дилатации для одномерного

b соответственно
Следовательно - f и b должны перекрываться
Если коэффициенты в

Особенности
Если коэффициенты в структурирующем элементе b больше нуля, то изображение становиться ярче

Темные детали ослабляются или пропадают в зависимости от соотношения их размеров и яркости с параметрами элемента b

нулю
Особенности
Если коэффициенты в структурирующем элементе b положительные, то изображение

и расширения
Замыкание - последовательное применение операций расширения и эрозии

Размыкание

Замыкание - для удаления небольших темных деталей на изображении

замыкание

Обработанное

Обработанное