Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Содержание
- 1. МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- 2. Способы решения тригонометрических уравненийУравнения , приводимые к квадратным уравнениямОднородные уравненияРазложение на множителиЗамена переменнойМетод вспомогательного углаПонижение степеней
- 3. МЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУ3sin2x – 5sinx – 2 = 02sin2x + 3cosx = 0
- 4. Уравнения, приводимые к квадратнымСхема решенияШаг 1. Привести уравнение
- 5. ответ: НЕ ИМЕЕТ РЕШЕНИЯМЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУ
- 6. МЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУ
- 7. МЕТОД СВЕДЕНИЯ УРАВНЕНИЯ К КВАДРАТНОМУНЕ ИМЕЕТ РЕШЕНИЯ ответ:
- 8. МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
- 9. ответ: МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
- 10. Уравнение вида аsinx + bcosx = 0 называют однородным
- 11. ОПРЕДЕЛЕНИЕ:Уравнение вида a sin2x + b sinx cosx + c cos²x = 0 называют однородным тригонометрическим уравнением второй степени.
- 12. Метод решения однородных уравнений (первой и второй
- 13. Метод решения однородных уравнений (первой и второй
- 14. Метод решения однородных уравнений (первой и второй
- 15. Метод решения однородных уравнений (первой и второй
- 16. ОДНОРОДНЫЕ УРАВНЕНИЯ5sinx + 6cosx = 03sin2x +sinxсosx =2cos2x
- 17. ОДНОРОДНЫЕ УРАВНЕНИЯ ответ:
- 18. ОДНОРОДНЫЕ УРАВНЕНИЯ
- 19. ОДНОРОДНЫЕ УРАВНЕНИЯ ответ:
- 20. Методы использования различных тригонометрических формулСхема решенияШаг 1. Используя
- 21. Методы использования различных тригонометрических формулПример.sin x +
- 22. Методы использования различных тригонометрических формулИз первого уравнения
- 23. Формулы.
- 24. Правила.Увидел квадрат – понижай степень.Увидел произведение – делай сумму. Увидел сумму – делай произведение.
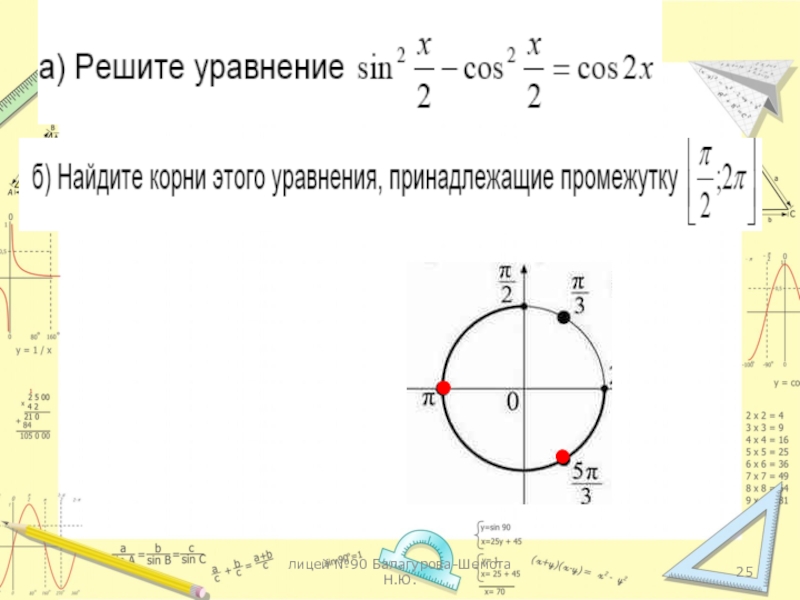
- 25. лицей №90 Балагурова-Шемота Н.Ю.
- 26. лицей №90 Балагурова-Шемота Н.Ю. , и .
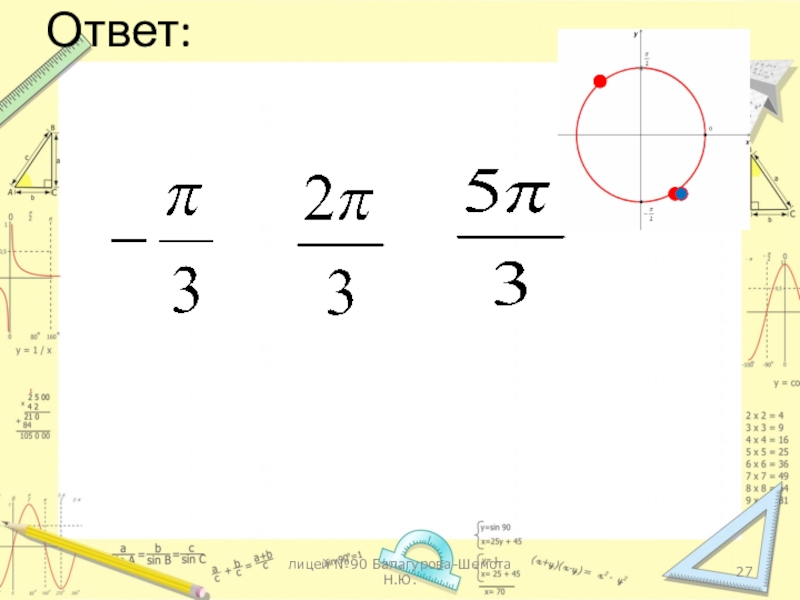
- 27. Ответ:лицей №90 Балагурова-Шемота Н.Ю.
- 28. лицей №90 Балагурова-Шемота Н.Ю.
- 29. Скачать презентанцию
Способы решения тригонометрических уравненийУравнения , приводимые к квадратным уравнениямОднородные уравненияРазложение на множителиЗамена переменнойМетод вспомогательного углаПонижение степеней
Слайды и текст этой презентации
Слайд 2Способы решения тригонометрических уравнений
Уравнения , приводимые к квадратным уравнениям
Однородные уравнения
Разложение
на множители
Слайд 4Уравнения, приводимые к квадратным
Схема решения
Шаг 1. Привести уравнение к алгебраическому виду
относительно одной из тригонометрических функций.
Шаг 2. Обозначить полученную функцию переменной t
(если необходимо, ввести ограничения на t).Шаг 3. Записать и решить полученное алгебраическое уравнение.
Шаг 4. Сделать обратную замену.
Шаг 5. Решить простейшее тригонометрическое уравнение.
Слайд 10Уравнение вида
аsinx + bcosx = 0
называют однородным тригонометрическим уравнение первой
степени.
ОПРЕДЕЛЕНИЕ:
Алгоритм решения однородного тригонометрического уравнения первой степени:
Деление обеих частей уравнения
на cosx, cosx ≠ 0.
Слайд 11ОПРЕДЕЛЕНИЕ:
Уравнение вида
a sin2x + b sinx cosx + c cos²x = 0
называют однородным тригонометрическим уравнением
второй степени.
Слайд 12Метод решения однородных уравнений (первой и второй степеней)
Схема решения
Шаг 1. Привести
данное уравнение к виду
a) a sin x + b cos
x = 0 (однородное уравнение первой степени)или к виду
б) a sin2 x + b sin x · cos x + c cos2 x = 0 (однородное уравнение второй степени).
Слайд 13Метод решения однородных уравнений (первой и второй степеней)
Шаг 2. Разделить обе
части уравнения на
а) cos x ≠ 0;
б) cos2 x ≠ 0;
и
получить уравнение относительно tg x:а) a tg x + b = 0;
б) a tg2 x + b arctg x + c = 0.
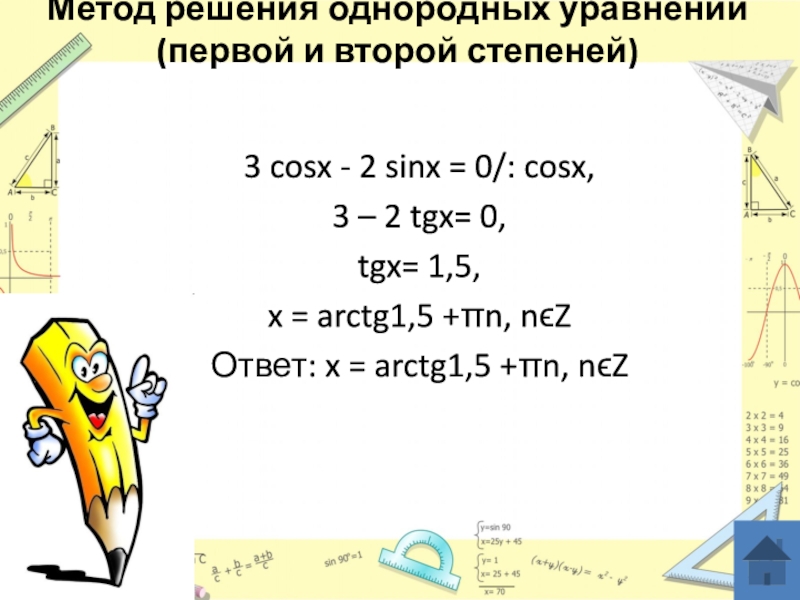
Пример 1: Решите уравнение
3 cosx - 2 sinx = 0.
Решение:
Слайд 14Метод решения однородных уравнений (первой и второй степеней)
3 cosx -
2 sinx = 0/: cosx,
3 – 2 tgx= 0,
tgx= 1,5,
x
= arctg1,5 +πn, nϵZОтвет: x = arctg1,5 +πn, nϵZ
Слайд 15Метод решения однородных уравнений (первой и второй степеней)
Пример 2:
5sin2 x +
3sin x · cos x – 4 = 0.
Решение.
1) 5sin2 x +
3sin x · cos x – 4(sin2 x + cos2 x) = 0;5sin2 x + 3sin x · cos x – 4sin² x – 4cos2 x = 0;
sin2 x + 3sin x · cos x – 4cos2 x = 0 /cos2 x ≠ 0.
Слайд 20Методы использования различных тригонометрических формул
Схема решения
Шаг 1. Используя всевозможные тригонометрические формулы,
привести данное уравнение к уравнению, решаемому методами I, II, III.
Шаг
2. Решить полученное уравнение известными методами.
Слайд 21Методы использования различных тригонометрических формул
Пример.
sin x + sin 2x +
sin 3x = 0.
Решение:
1) (sin x + sin 3x) + sin
2x = 0;2sin 2x · cos x + sin 2x = 0.
2) sin 2x · (2cos x + 1) = 0;
sin 2x = 0 или 2cos x + 1 = 0;
Слайд 22Методы использования различных тригонометрических формул
Из первого уравнения
2x = π/2
+ πn, n ϵZ;
из второго уравнения: cos x =
-1/2.Имеем х = π/4 + πn/2, n ϵ Z;
получим x = ±(π – π/3) + 2πk, k ϵ Z.
В итоге х = π/4 + πn/2, n ϵ Z;
x = ±2π/3 + 2πk, k ϵ Z.
Ответ: х = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k ϵ Z.
Слайд 23Формулы.
Универсальная
подстановка.
х + 2n;
Проверка обязательна!Понижение степени.
= (1 + cos2x ) : 2
= (1 – cos 2x) : 2
Метод вспомогательного аргумента.
Слайд 24Правила.
Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел
сумму – делай произведение.
