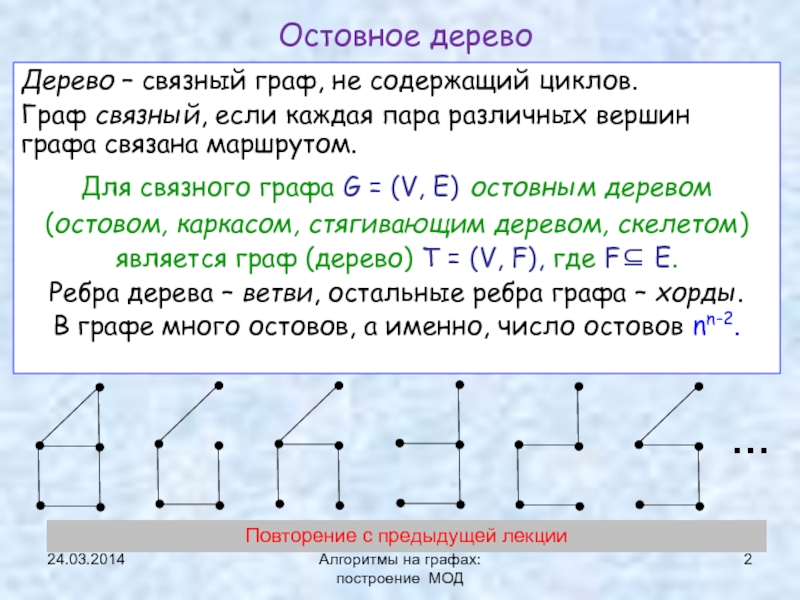
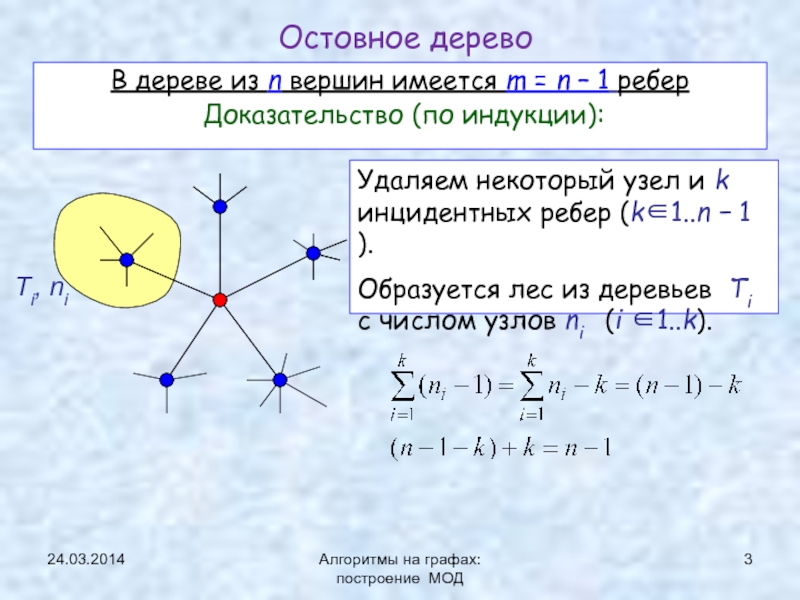
Минимальное остовное дерево (МОД)
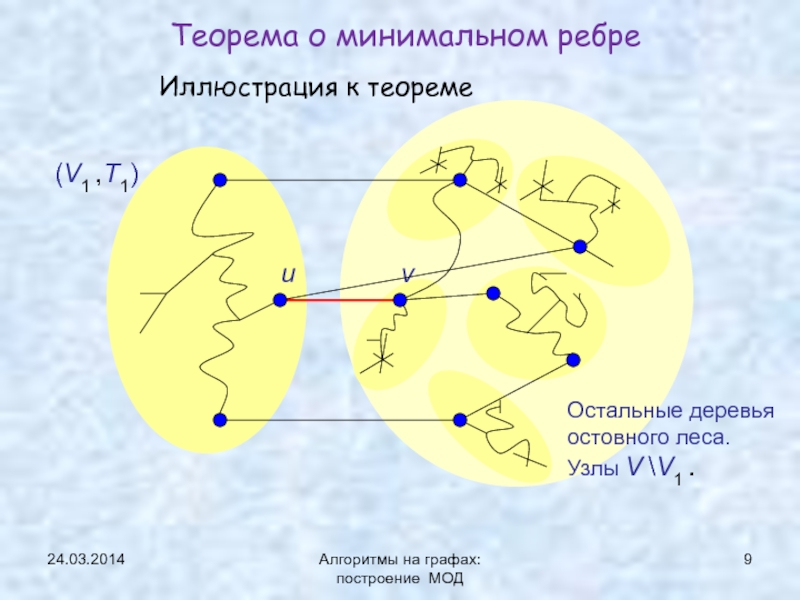
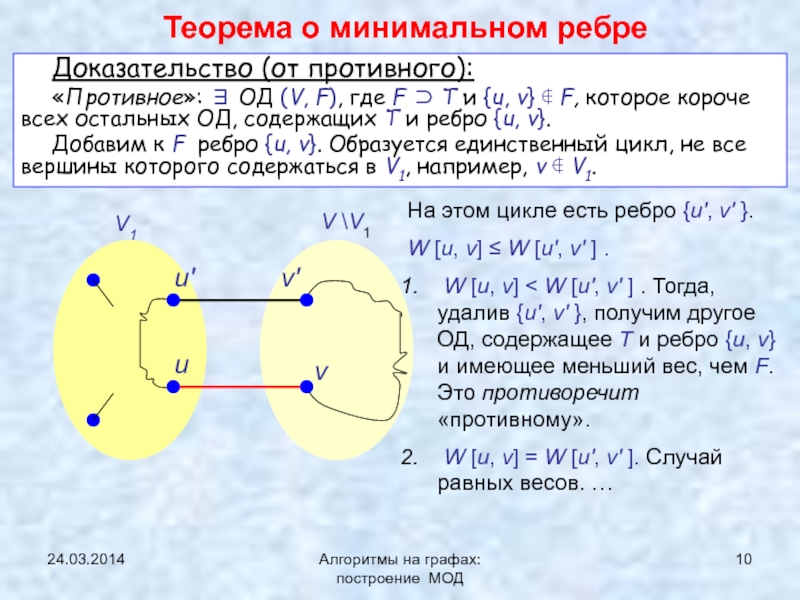
Теорема о минимальном ребре
Алгоритм Краскала (Жадный алгоритм)
Алгоритм
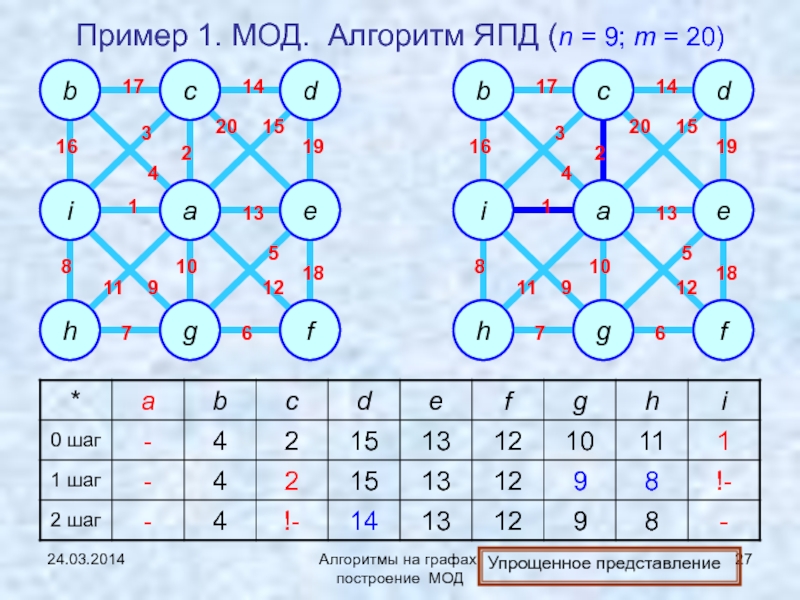
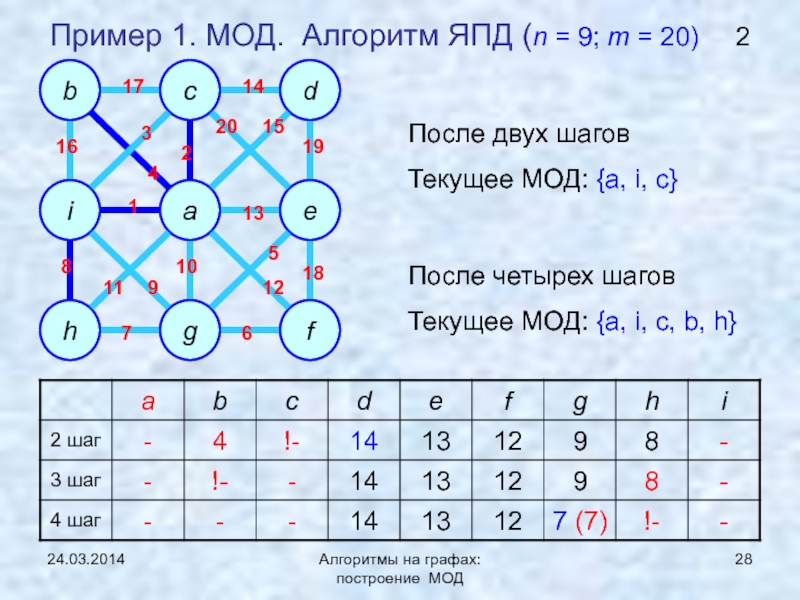
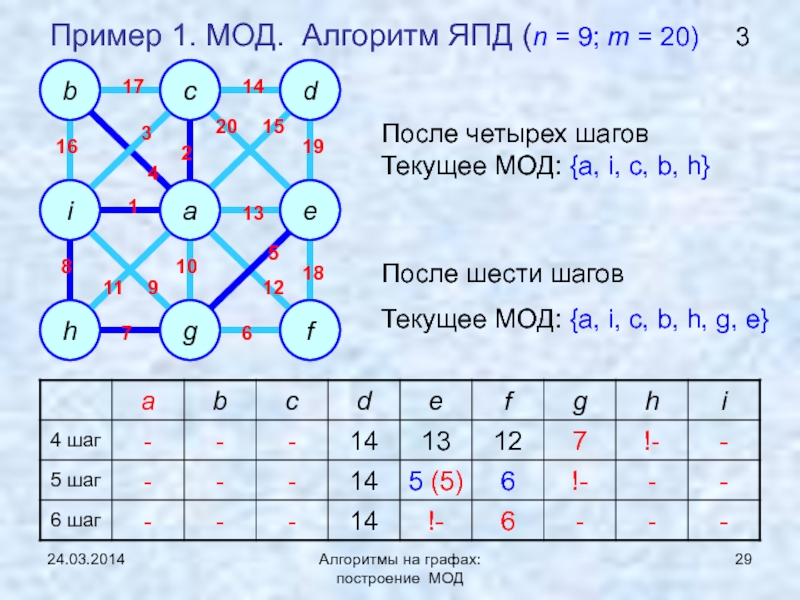
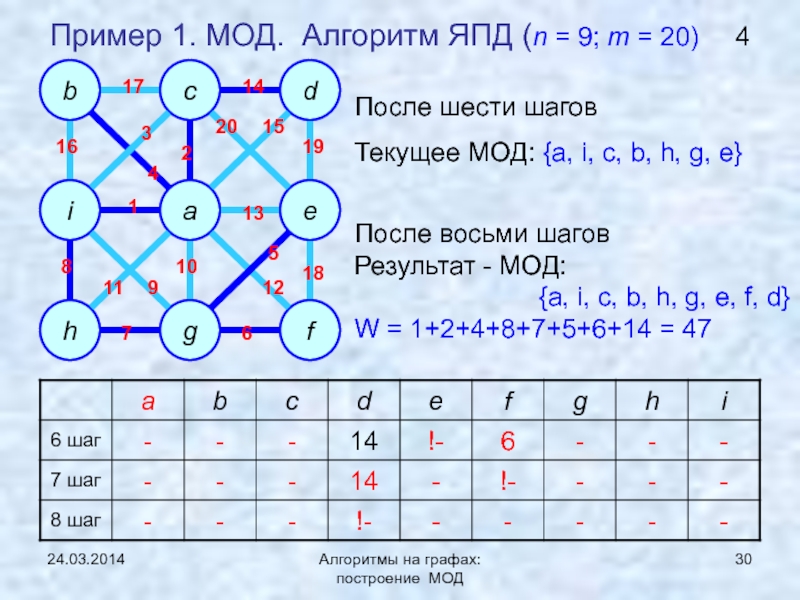
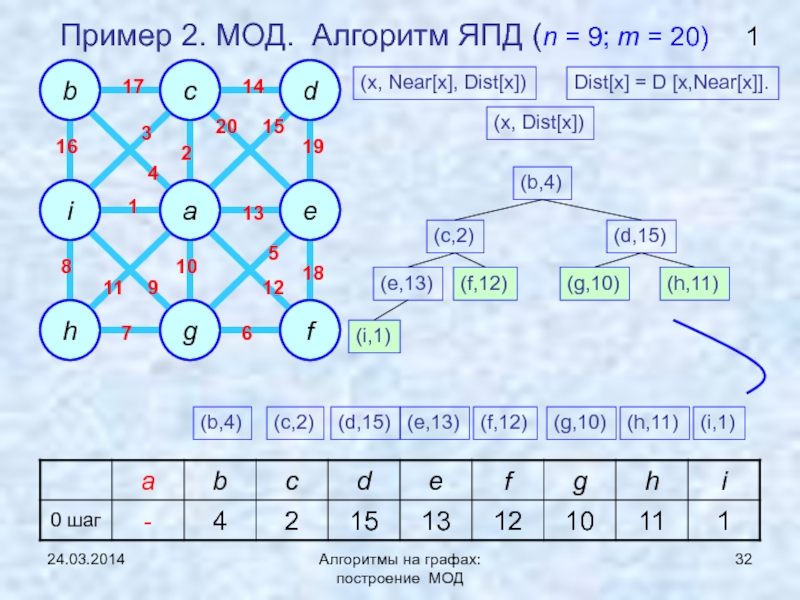
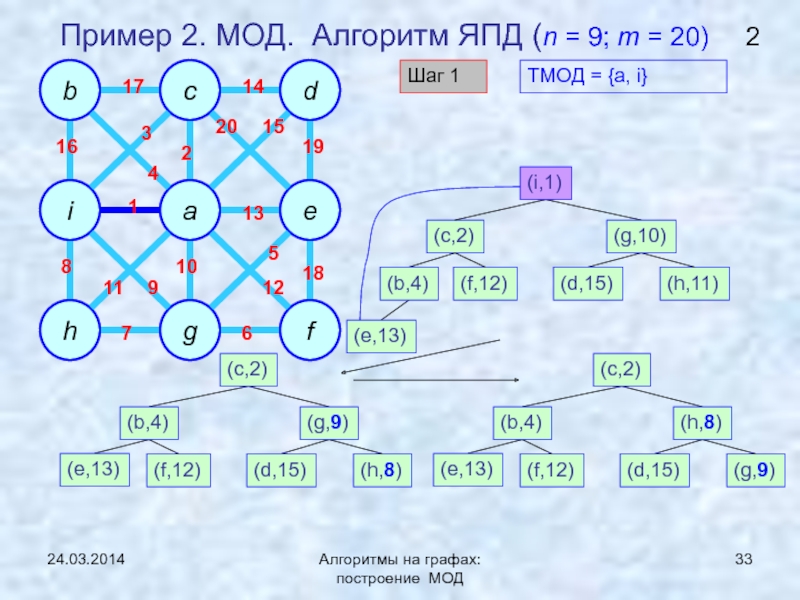
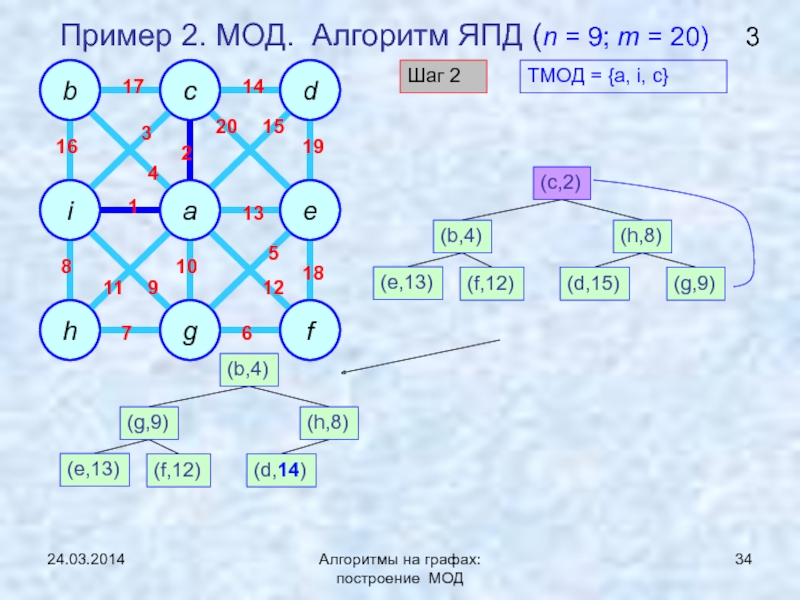
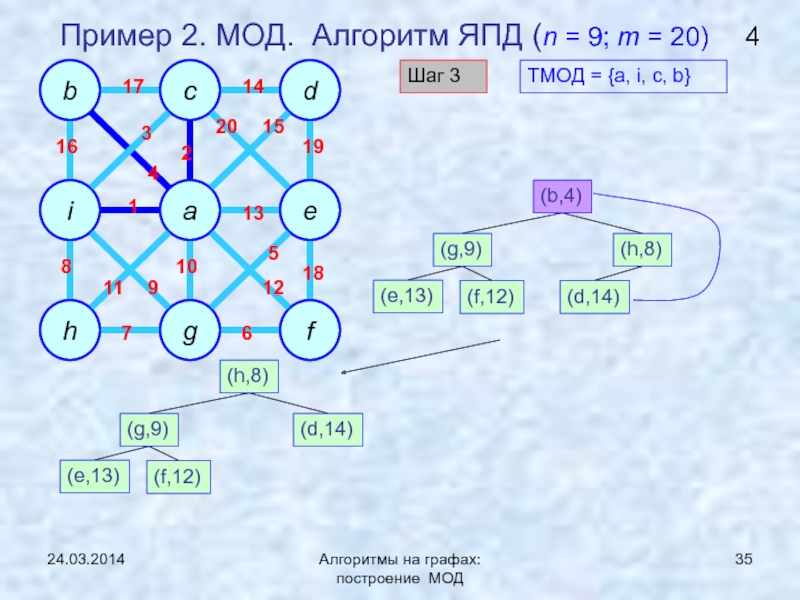
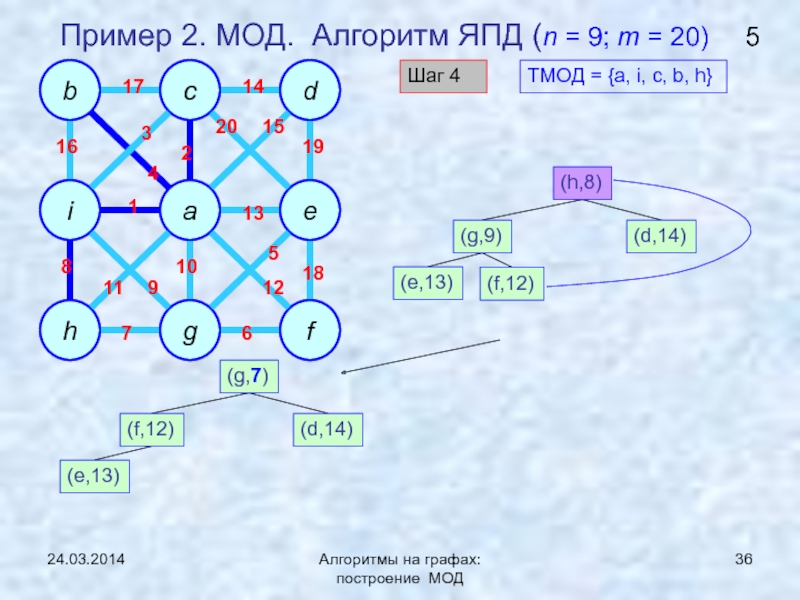
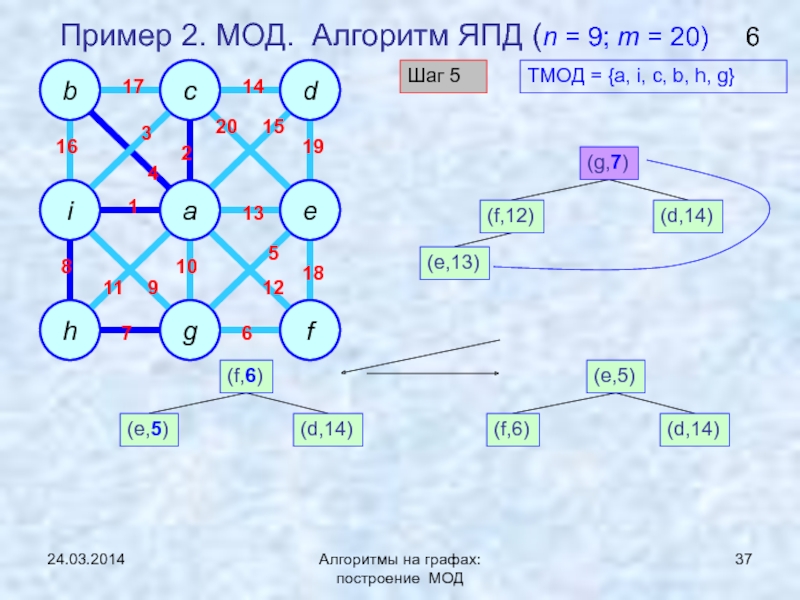
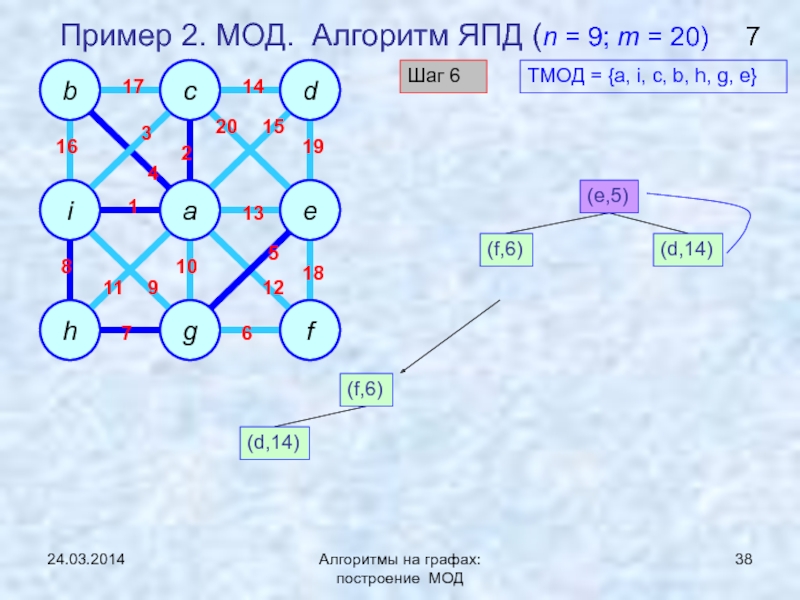
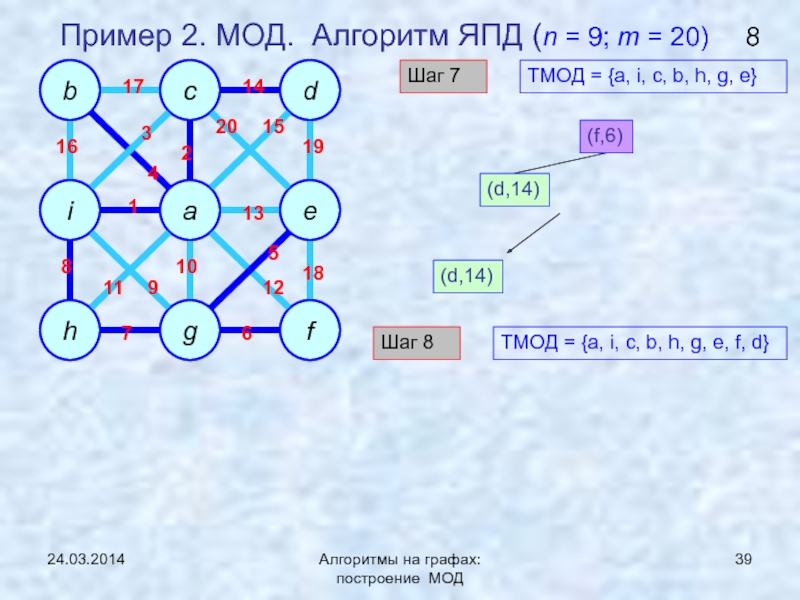
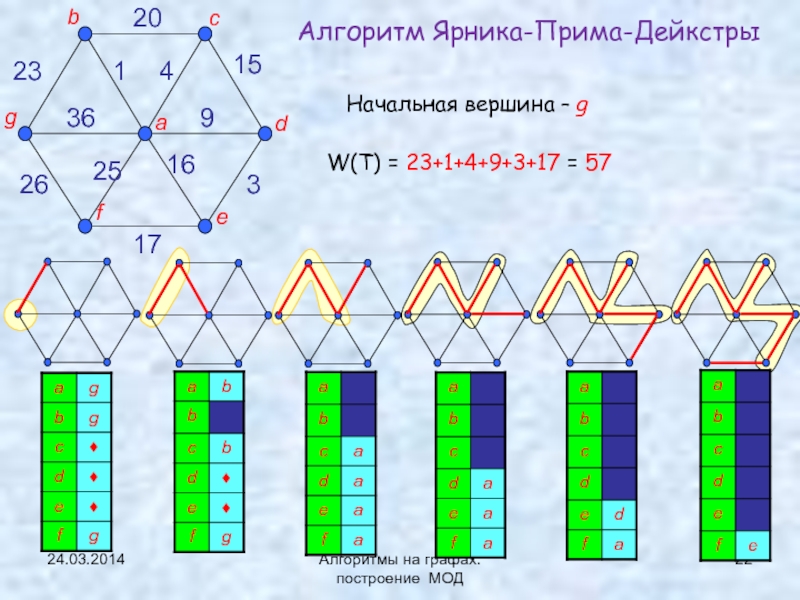
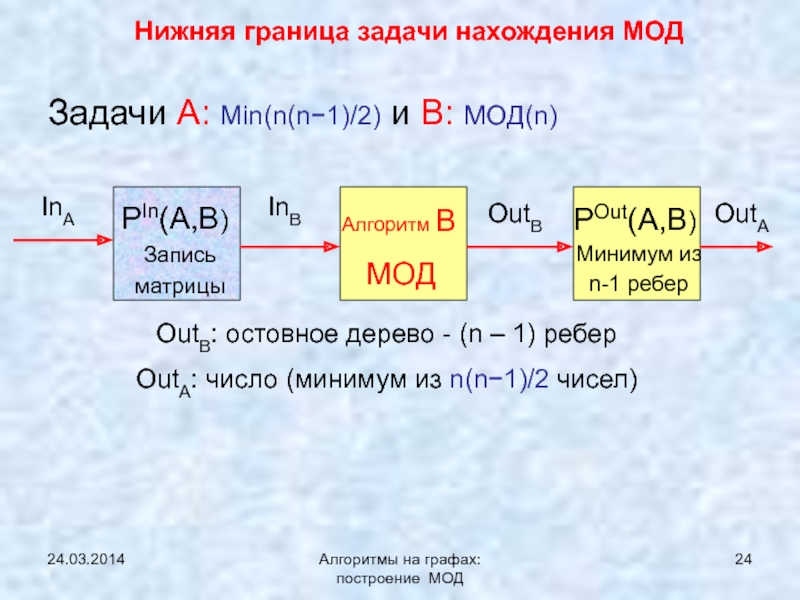
ЯПД (Ярника-Прима-Дейкстры)Нижняя граница задачи нахождения МОД
Построение и анализ алгоритмов

![Минимальное остовное дерево (МОД) Теорема о минимальном ребре Алгоритм Краскала 24.03.2014Алгоритмы на графах: построение МОДГраф G = (V, E). Матрица весов 24.03.2014Алгоритмы на графах: построение МОДГраф G = (V, E). Матрица весов W[v, u]. Пусть T = (V,](/img/tmb/2/153230/032f7f519d86aaeb278be65c8a0272b9-800x.jpg)






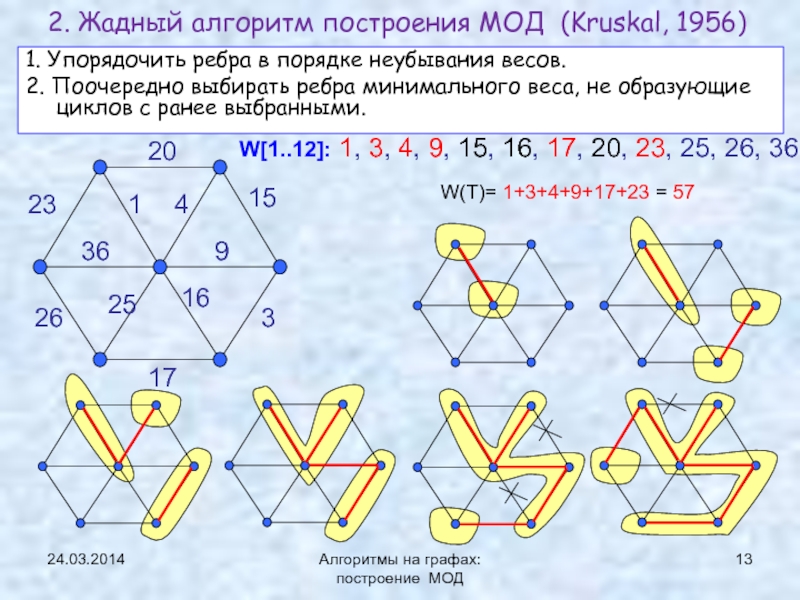

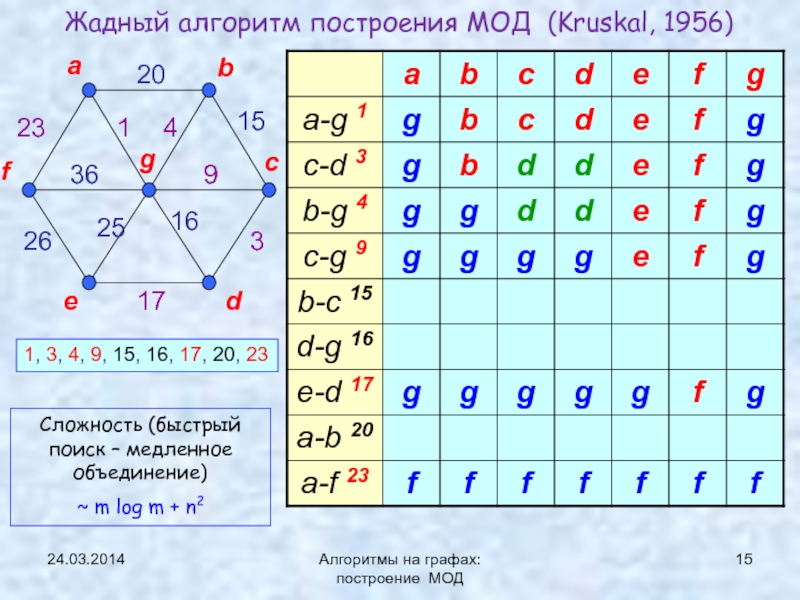

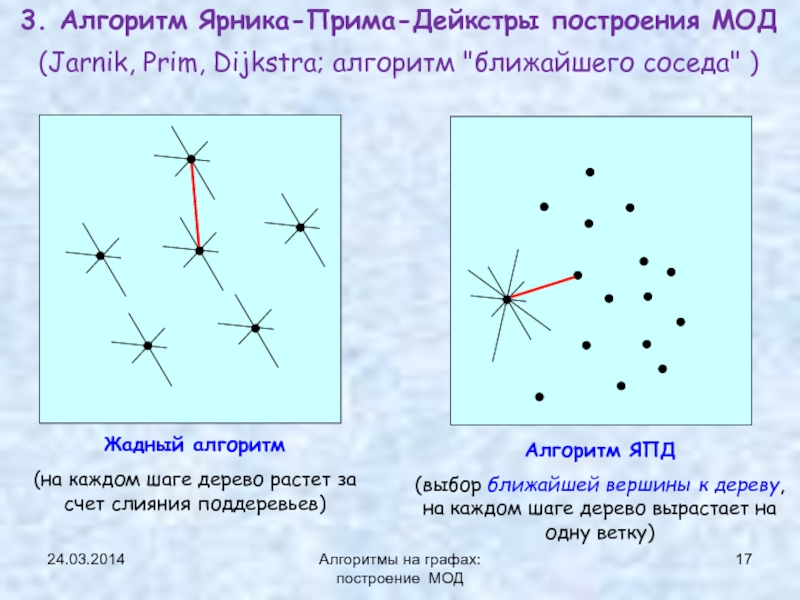

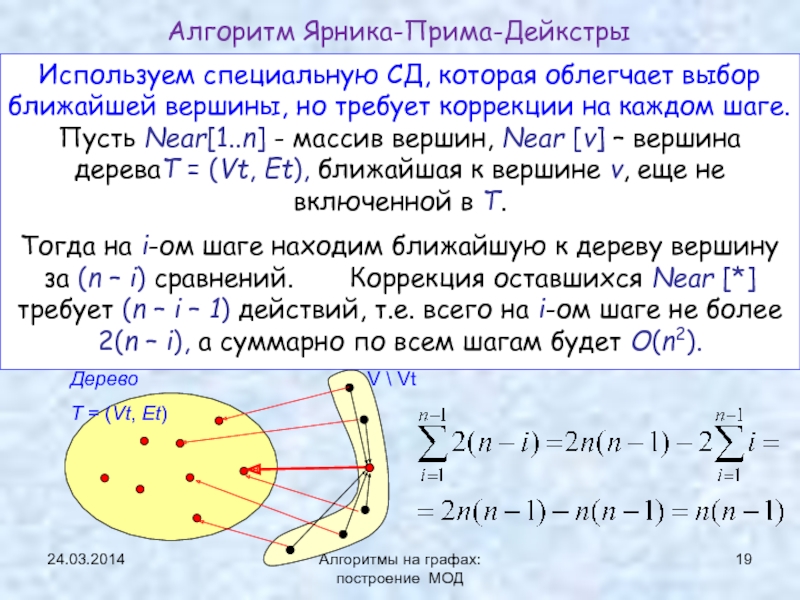
![Минимальное остовное дерево (МОД) Теорема о минимальном ребре Алгоритм Краскала 24.03.2014Алгоритмы на графах: построение МОДВход : V - множество вершин графа 24.03.2014Алгоритмы на графах: построение МОДВход : V - множество вершин графа G=(V,E), а D [1..n,1..n] – матрица](/img/thumbs/cdf0ebf3adfa1659b747efd7ef65774d-800x.jpg)


![Минимальное остовное дерево (МОД) Теорема о минимальном ребре Алгоритм Краскала 24.03.2014Алгоритмы на графах: построение МОДПусть наряду с Near[*] используется рабочий массив 24.03.2014Алгоритмы на графах: построение МОДПусть наряду с Near[*] используется рабочий массив расстояний Dist[x] = D [x,Near[x]].](/img/thumbs/4becedef023af9103f9503587567f2ad-800x.jpg)