удобно минимизировать путем сравнения рабочих и запрещенных наборов. Задача заключается
в том, чтобы в каждом рабочем наборе оставить минимальное количество переменных, позволяющих отличить этот набор от всех запрещенных наборов.Покажем это на примере минимизации функции «импликация х в y»:





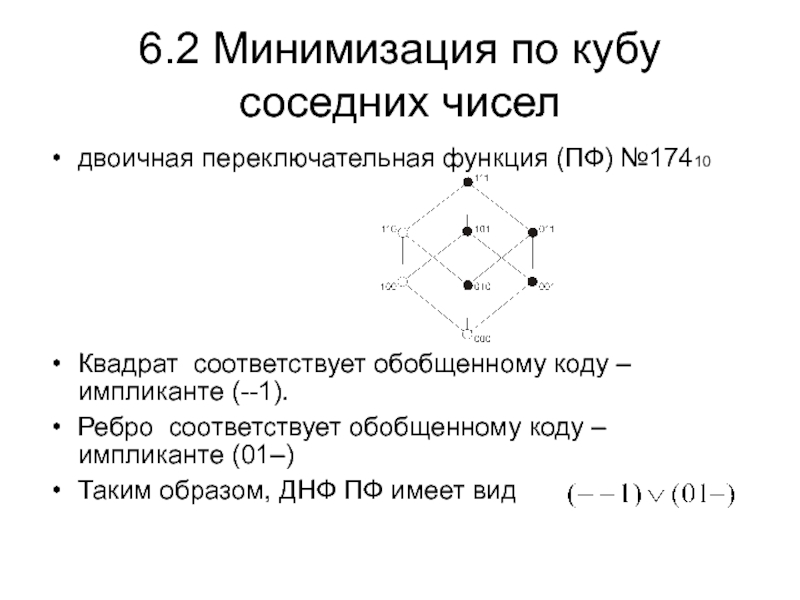







![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. ВикентьеваПРИМЕР.Задана функция в восьмеричной системе счисления:f8(х6х5х4х3х2х1)=56[26]. Метод Л.Ф. ВикентьеваПРИМЕР.Задана функция в восьмеричной системе счисления:f8(х6х5х4х3х2х1)=56[26].](/img/thumbs/b8300c7e5f535a075594c993c216c100-800x.jpg)
![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. Викентьеваf8(х6х5х4х3х2х1)=56[26].Всего существует 64 набора переменных для функции 6 переменных. Метод Л.Ф. Викентьеваf8(х6х5х4х3х2х1)=56[26].Всего существует 64 набора переменных для функции 6 переменных. Как видно, используется только один рабочий](/img/thumbs/26a7ed31d3bb980e2ac7ec719dbd3fc0-800x.jpg)
![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. Викентьеваf8(х6х5х4х3х2х1)=56[26].Каждое рабочее число соответствует члену СДНФ. Восьмеричная система позволяет Метод Л.Ф. Викентьеваf8(х6х5х4х3х2х1)=56[26].Каждое рабочее число соответствует члену СДНФ. Восьмеричная система позволяет очень легко переходить к СДНФ. Каждый](/img/thumbs/9422a04581664d382265fab4e772aeb8-800x.jpg)
![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. ВикентьеваТаким образом, говорят, что ранг такого представления =6. f8(х6х5х4х3х2х1)=56[26].Определим Метод Л.Ф. ВикентьеваТаким образом, говорят, что ранг такого представления =6. f8(х6х5х4х3х2х1)=56[26].Определим запрещенные числа для старшего разряда числа](/img/thumbs/5b6a6ff6f88c0306f86e62031ed26bfe-800x.jpg)


![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. ВикентьеваМинимизируем функцию трех переменных f8 (х6х5х4)= 5[2] по кубу соседних чисел Метод Л.Ф. ВикентьеваМинимизируем функцию трех переменных f8 (х6х5х4)= 5[2] по кубу соседних чисел](/img/thumbs/e9c7f45d4215ddbdf1189f75bdce5c53-800x.jpg)
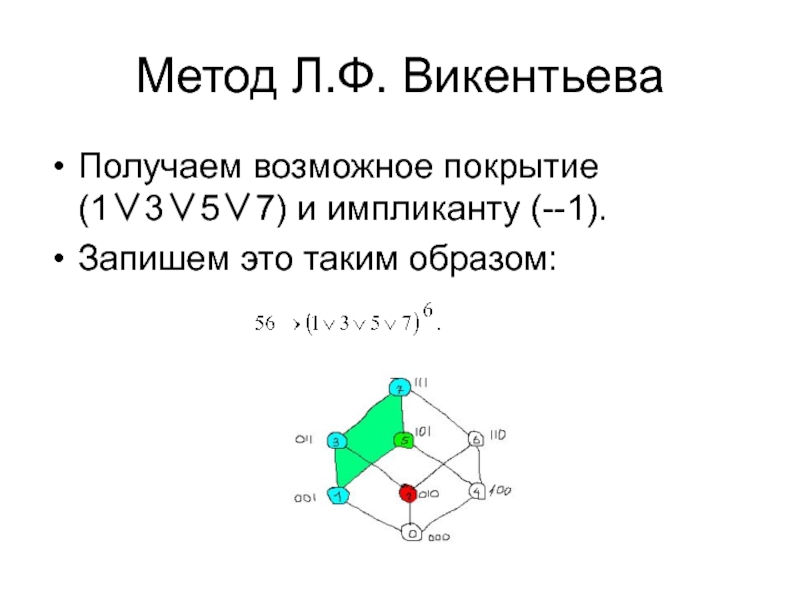

![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. Викентьеваf8(х6х5х4х3х2х1)=56[26].Теперь нужно аналогичным образом минимизировать младший разряд рабочего числа. Метод Л.Ф. Викентьеваf8(х6х5х4х3х2х1)=56[26].Теперь нужно аналогичным образом минимизировать младший разряд рабочего числа. Определим возможные наборы, которые могут получиться](/img/thumbs/9981347178c83036c8d8c82e44f4b7e1-800x.jpg)



![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. ВикентьеваПРИМЕР 2. f8(х5х4х3 х2х1)=37,22,31[00,16,10]. Метод Л.Ф. ВикентьеваПРИМЕР 2. f8(х5х4х3 х2х1)=37,22,31[00,16,10].](/img/thumbs/f7724dfc03c826a02f39435cbb6a9251-800x.jpg)
![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. ВикентьеваПРИМЕР 2. f8(х5х4х3 х2х1)=37,22,31[00,16,10].Итак, f8(х5х4х3х2х1)=(--)(--1)∨(--)(01-)= Здесь в первом разряде Метод Л.Ф. ВикентьеваПРИМЕР 2. f8(х5х4х3 х2х1)=37,22,31[00,16,10].Итак, f8(х5х4х3х2х1)=(--)(--1)∨(--)(01-)= Здесь в первом разряде обобщенных кодов два (символов «тире»), т.к.](/img/thumbs/764e56debbc95a7ef81837ca6266995e-800x.jpg)
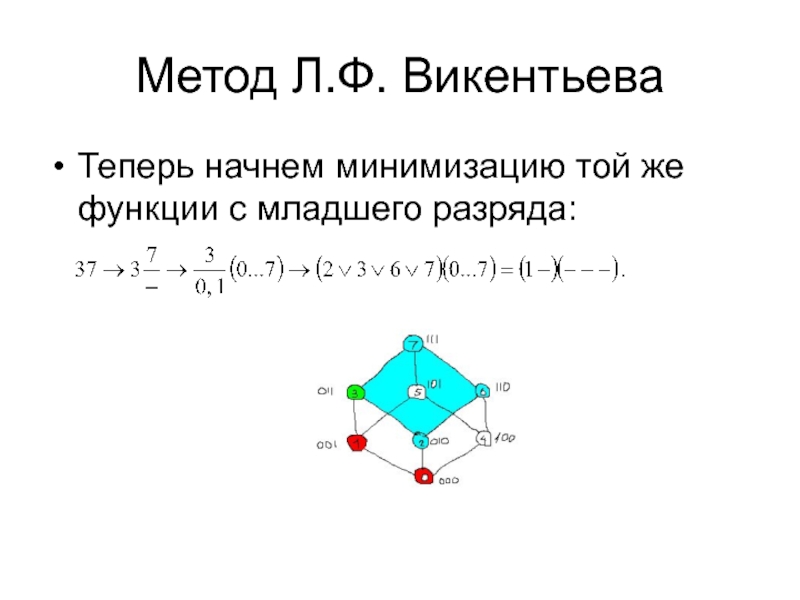
![МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ методом Л.Ф.Викентьева Метод Л.Ф. ВикентьеваПолучили f8(х5х4х3 х2х1)= x5. f8(х5х4х3 х2х1)=37,22,31[00,16,10].Очевидно, x5 покрывает все Метод Л.Ф. ВикентьеваПолучили f8(х5х4х3 х2х1)= x5. f8(х5х4х3 х2х1)=37,22,31[00,16,10].Очевидно, x5 покрывает все рабочие числа 37, 22, 31.Видим, что](/img/thumbs/63cecb8283c1a090e43662c9c01446e0-800x.jpg)