МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ МЕДИЧНИЙ КОЛЕДЖ ЛЬВІВСЬКОГО НАЦІОНАЛЬНОГО

МІНІСТЕРСТВО ОСВІТИ І НАУКИ

УКРАЇНИ МЕДИЧНИЙ КОЛЕДЖ ЛЬВІВСЬКОГО НАЦІОНАЛЬНОГО МЕДИЧНОГО УНІВЕРСИТЕТУ ІМЕНІ ДАНИЛА ГАЛИЦЬКОГО Дослідницька робота на тему: “Електроємність. Конденсатори та їхнє використання в техніці. Енергія електричного поля.” Виконала: студентка групи 1-В Іванцік О.А. Перевірила: викладач фізики Басай М.В. ЛЬВІВ 2014

відношення заряду до потенціалу для даного провідника — величина постійна,

яка залежить від його розмірів і форм.
Відношення заряду відокремленого провідника до його потенціалу, тобто величину C, називають електроємністю цього провідника.

На честь англійського фізика М.Фарадея ця одиниця

названа фарадом.
1 фарад — ємність провідника, у якого зміна заряду на 1 Кл спричиняє зміну потенціалу на 1 В.
Для практичних цілей використовують малі частинки фарада: 1 мкФ ; 1 пФ.

провідних пластин, розташованих паралельно один до одного на малій порівняно

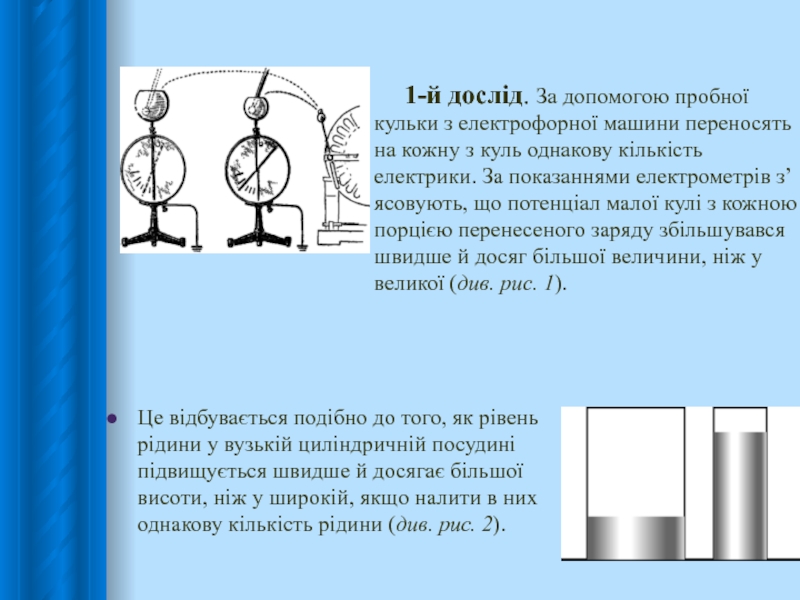
з розмірами пластин відстані й розділених шаром діелектрика. Такий конденсатор називається плоским.

циліндричній посудині підвищується швидше й досягає більшої висоти, ніж у

широкій, якщо налити в них однакову кількість рідини (див. рис. 2).

1-й дослід. За допомогою пробної кульки з електрофорної машини переносять на кожну з куль однакову кількість електрики. За показаннями електрометрів з’ясовують, що потенціал малої кулі з кожною порцією перенесеного заряду збільшувався швидше й досяг більшої величини, ніж у великої (див. рис. 1).

що потенціали куль стали рівними. Після з’єднання відбувалося переміщення заряду

у бік зниження потенціалу, тобто від малої кулі до більшої, поки потенціали не вирівнялися. Отже, тепер на кулях заряди не рівні; у великої кулі заряд більший, ніж у малої. Це аналогічно явищу, що відбувається під час з’єднання двох посудин різного поперечного перерізу, у яких рівні рідини спочатку перебувають на різній висоті, а після з’єднання вирівнюються (див. рис. 3).

заряду, а відношення заряду до потенціалу для даного провідника

— величина постійна, яка залежить від його розмірів і форм і називається електроємністю провідника: .

дорівнює:


Робота, здійснювана електричним полем під час

розряджання конденсатора:

зарядженого до напруги U , дорівнює:

Задача №1
Плоский повітряний конденсатор має електроємність C

і заряджений до напруги U. Яку роботу треба зробити, щоб збільшити відстань між його обкладками вдвічі?
Розв'язок:
При збільшенні відстані між обкладками в два рази, у два рази зменшується електроємність конденсатора. Так як при цьому заряд на пластинах не змінюється, в два рази збільшується напруга між ними. Отже:
W=C'*U'*U'/2;
C'=C/2;
U'=2U
=>


Відповідь: A=C*U*U/2.

Задача №2
Конденсатор електроємністю 3 мкФ заряджений до напруги 300

В, а конденсатор електроємністю 2 мкФ - до 200 В. Після зарядки конденсатори з'єднали однойменними полюсами. Яка напруга встановиться між обкладками конденсаторів після з'єднання?
Розв'язок:
Так як конденсатори з'єднані паралельно, їх загальна електроємність дорівнює: C = C1 + C2; 
А сумарний заряд дорівнює q=q1+q2;
Так як з'єднувалися однойменні обкладки, то шукана напруга дорівнює:

Так, як:

Тоді:


Відповідь: U=260*e 

Розв'язок:
Якщо прийняти потенціали точок A, B, D, F за нуль, а потенціал точок K, L, M за U, то потенціал точки N буде не більше U, а потенціал точки P - не більше потенціалу точки N.
Позначимо потенціал точки P через x, а потенціал точки N через y. Тоді U ≥ x ≥ y ≥ 0.
q1 = C ∙ (U - y), q2 = C ∙ (U - x), q3 = C ∙ (x - y), q4 = C ∙ U, q5 = C ∙ x, q6 = C ∙ y.
Так як q2 = q3 + q5, q6 = q1 + q3, то
C ∙ (U - x) = C ∙ (x - y) + C ∙ x;
C ∙ y = C ∙ (U - y) + C ∙ (x - y).
Рішення системи рівнянь дає:



Відповідь: C'=2*C

навколо заряду.
Частинка, яка рухається навколо ядра атома.
Одиниця заряду в системі

СІ.
Матеріал, який не проводить електричний струм.
Векторна величина, яка чисельно дорівнює відношенню сили, з якою поле діє на точковий заряд, до величини цього заряду.
Одиниця вимірювання потенціалу.
Між зарядами відбувається електромагнітна …
Один із зарядів.
Енергетична характеристика електричного поля.
Явище електростатичної …
Електричне поле, яке існує навколо нерухомих зарядів.
Прилад для вимірювання різниці потенціалів.
Одиниця вимірювання енергії.