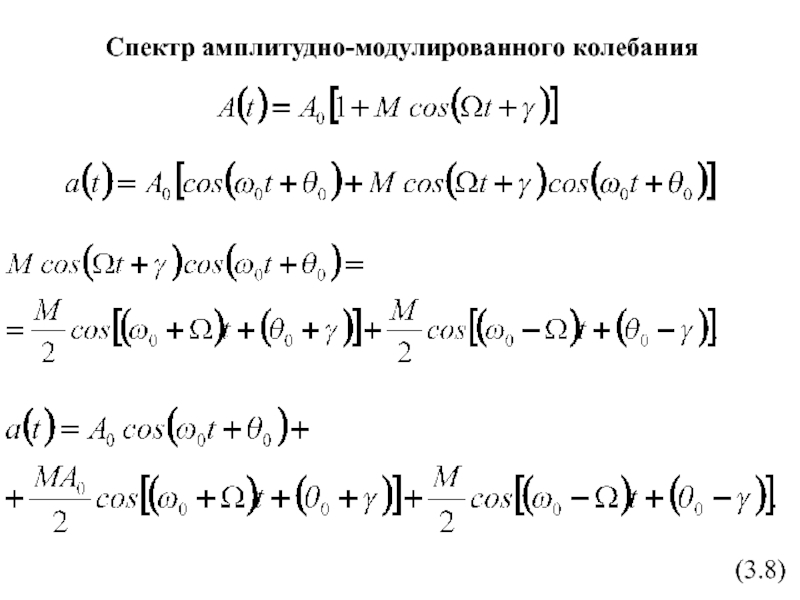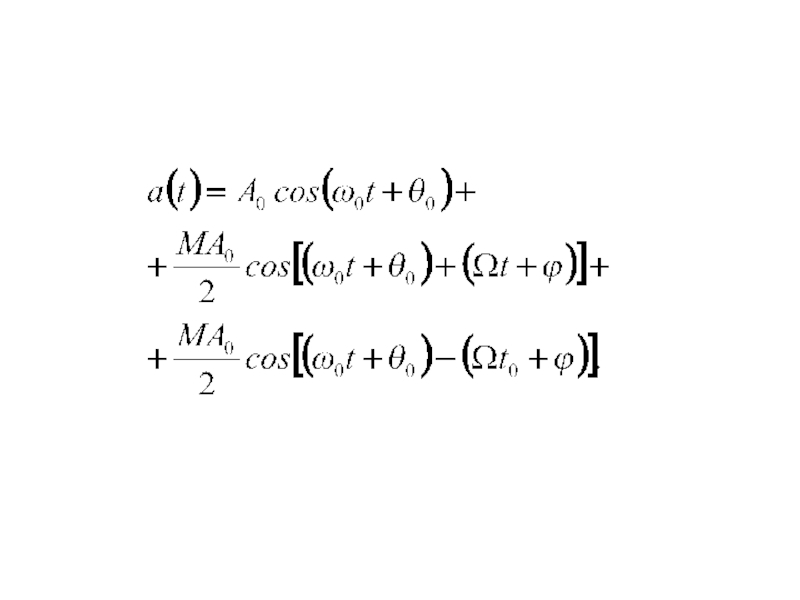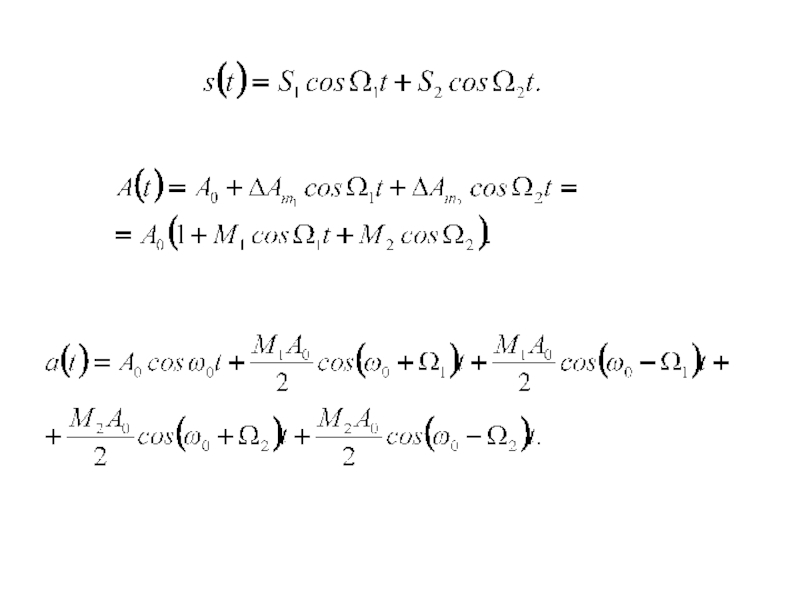Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модулирование колебания
Содержание
- 1. Модулирование колебания
- 2. или(3.3)Так как обычно ω(t) очень мало отличается от ω0, можно считать Т≈2π/ω0 и исходить из условия
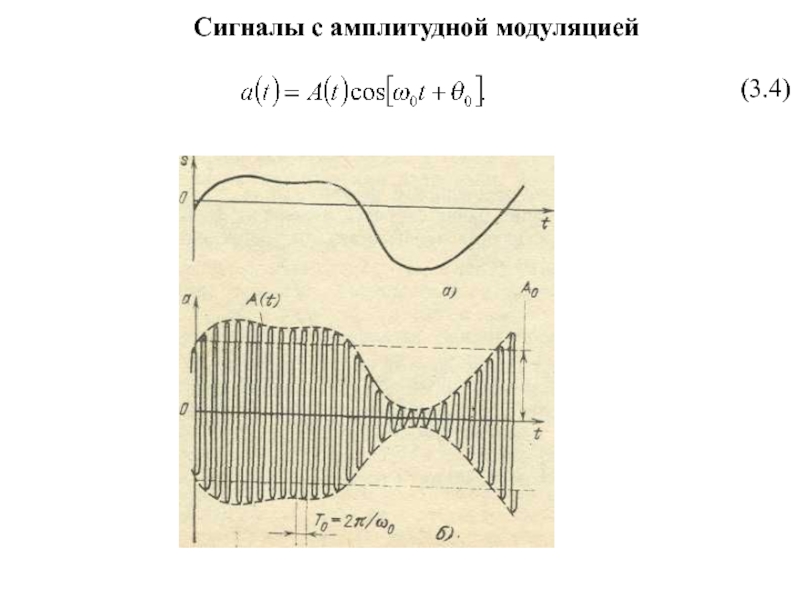
- 3. Сигналы с амплитудной модуляцией(3.4)
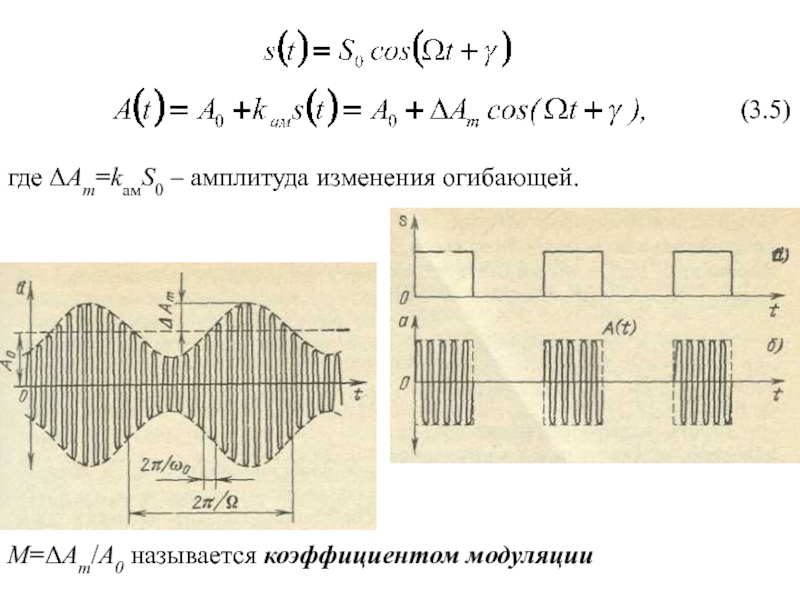
- 4. (3.5)М=ΔAm/A0 называется коэффициентом модуляции где ΔAm=kамS0 – амплитуда изменения огибающей.
- 5. (3.6)(3.7)При неискаженной модуляции (М≤1) амплитуда колебания изменяется
- 6. Спектр амплитудно-модулированного колебания(3.8)
- 7. Слайд 7
- 8. Слайд 8
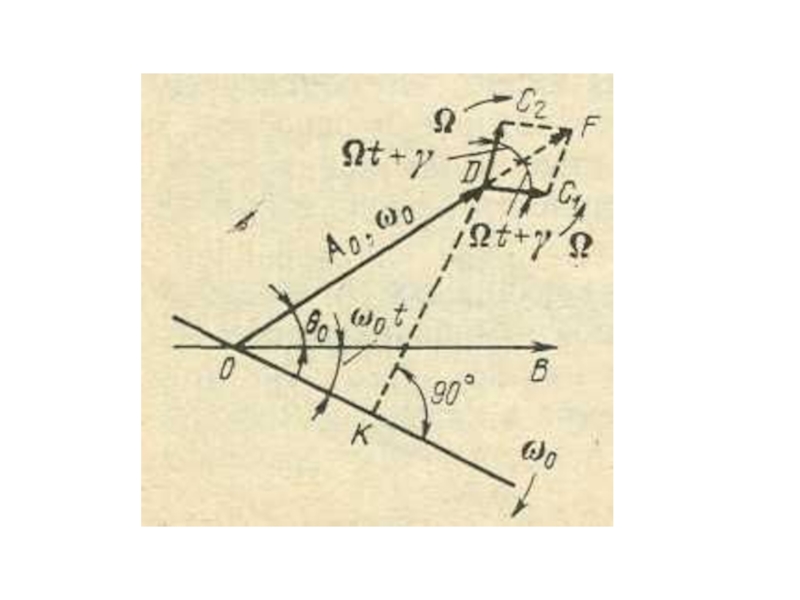
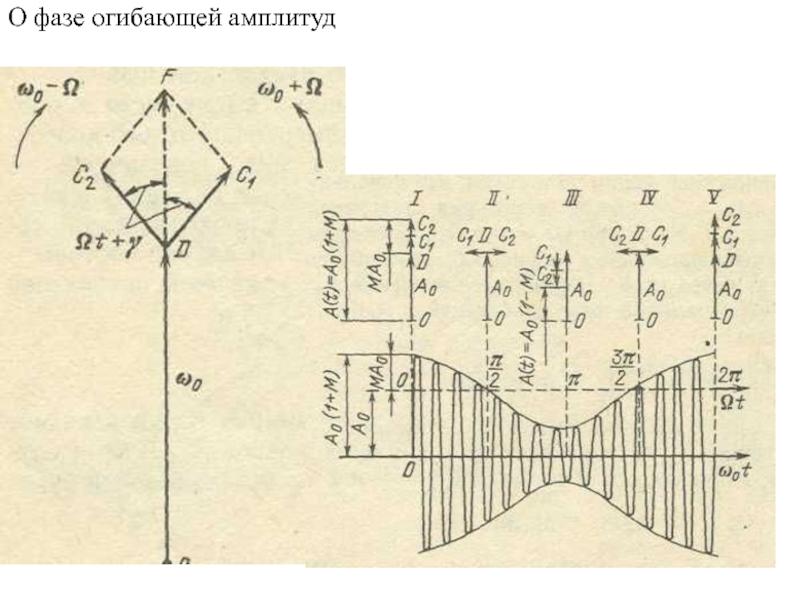
- 9. О фазе огибающей амплитуд
- 10. Спектр колебания при тональной (гармонической) AM
- 11. Слайд 11
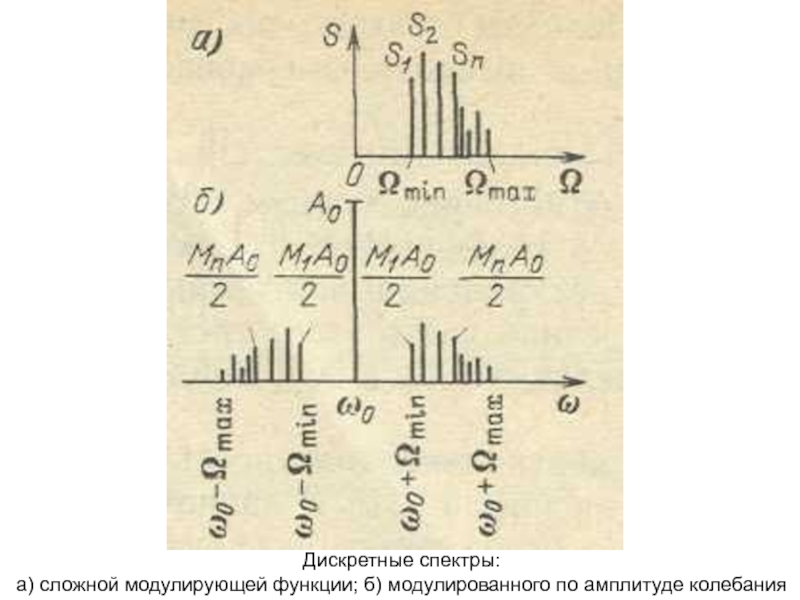
- 12. Дискретные спектры:а) сложной модулирующей функции; б) модулированного по амплитуде колебания
- 13. (3.9) Для узкополосного сигнала можно считать, что в областиположительных частот(3.10) а в области отрицательных частот(3.10`)
- 14. Сплошная часть
- 15. Спектр прямоугольного радиоимпульса (3.12)
- 16. (3.13) Огибающая амплитуд колебания a(t)а спектральная плотность этой огибающей (3.14)
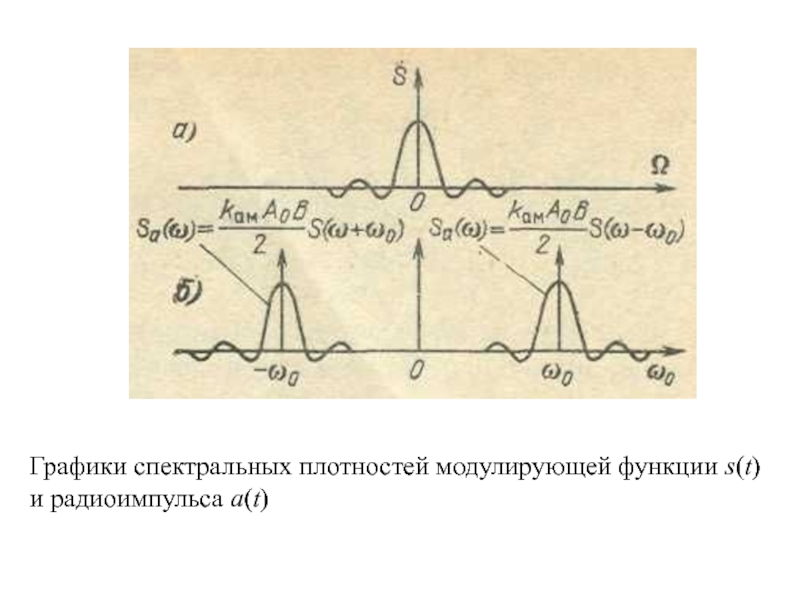
- 17. Графики спектральных плотностей модулирующей функции s(t)и радиоимпульса a(t)
- 18. Скачать презентанцию
или(3.3)Так как обычно ω(t) очень мало отличается от ω0, можно считать Т≈2π/ω0 и исходить из условия
Слайды и текст этой презентации
Слайд 2
или
(3.3)
Так как обычно ω(t) очень мало отличается от ω0, можно
считать Т≈2π/ω0 и исходить из условия
Слайд 4
(3.5)
М=ΔAm/A0 называется коэффициентом модуляции
где ΔAm=kамS0 – амплитуда изменения огибающей.
Слайд 5
(3.6)
(3.7)
При неискаженной модуляции (М≤1) амплитуда колебания
изменяется от минимальной Amin=A0(1–М)
до максимальной
Amax=A0(1+М).
Средняя за период модуляции мощность равна
Пикам соот-ет
мощность (1+М)2 Р0, где Р0=(1/2)A02 - мощность несущейПри 100 %-ной модуляции (М=1) пиковая мощность равна 4Р0,
а средняя мощность 1,5Р0
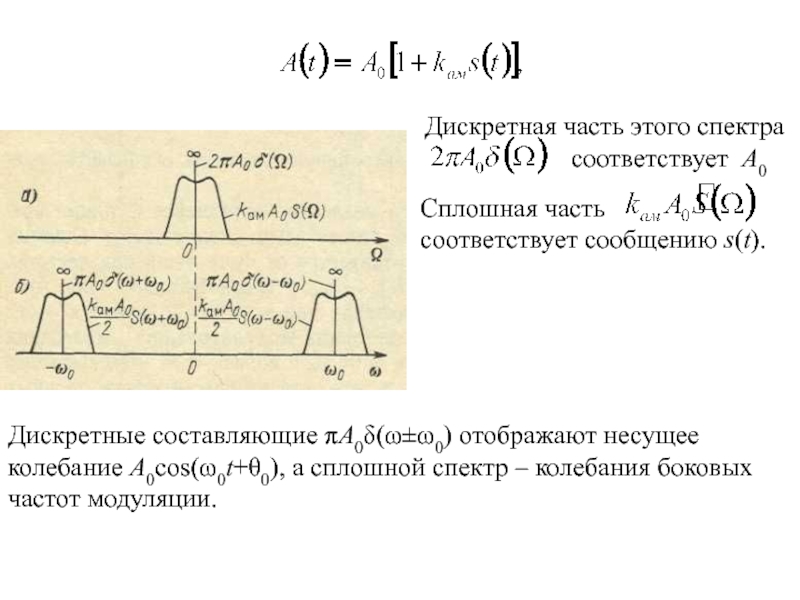
Слайд 12Дискретные спектры:
а) сложной модулирующей функции; б) модулированного по амплитуде колебания
Слайд 13
(3.9)
Для узкополосного сигнала можно считать, что в области
положительных частот
(3.10)
а в области отрицательных частот
(3.10`)
Слайд 14
Сплошная часть
соответствует сообщению s(t).
Дискретные составляющие πA0δ(ω±ω0)
отображают несущееколебание А0cos(ω0t+θ0), а сплошной спектр – колебания боковых
частот модуляции.
Дискретная часть этого спектра
соответствует А0